4.1 比例线段 课件(共40张PPT)-2023-2024学年九年级数学上册同步精品课堂(浙教版)
文档属性
| 名称 | 4.1 比例线段 课件(共40张PPT)-2023-2024学年九年级数学上册同步精品课堂(浙教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 06:58:16 | ||
图片预览










文档简介
4.1 比例线段
数学(浙教版)
九年级 上册
第4章 相似三角形
学习目标
1、理解并掌握线段的比、成比例线段的概念和相关组成元素;
2、理解并能灵活运用比例的基本性质解决问题;
3、掌握黄金分割的相关概念与应用;
导入新课
问题:两组图中A、B之间有何关系?
A B
【分析】形状相同、大小相等——全等
导入新课
问题:两组图中A、B之间有何关系?
A B
A B
【分析】形状相同、但是大小不等
讲授新课
知识点一 线段的比
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比.
其中,线段AB,CD分别叫做这个线段比的前项和后项.
讲授新课
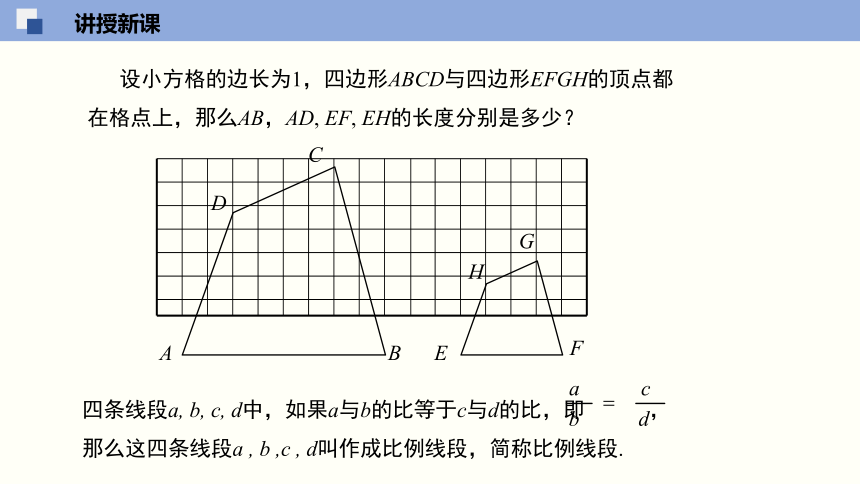
设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,AD, EF, EH的长度分别是多少?
四条线段a, b, c, d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a , b ,c , d叫作成比例线段,简称比例线段.
A
B
C
D
G
H
E
F
讲授新课
典例精析
【例1】已知AB长为1dm,CD长为2cm,则AB:CD=________.
【分析】
∵AB=1dm=10cm
∴AB:CD=10:2=5:1
【总结】
(1)计算线段的比,即计算线段长度的比
(2)需保证长度的单位统一
讲授新课
1.已知教室黑板的长 a = 3.2 m,宽 b = 120 cm ,求 a:b。
∴a :b = 320 :120 = 8 :3
或:
2.一条线段的长度是另一条线段长度的 ,则这两条线段之比是?
∵a=3.2m=320cm
练一练
讲授新课
知识点二 成比例线段的概念
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即:
那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
讲授新课
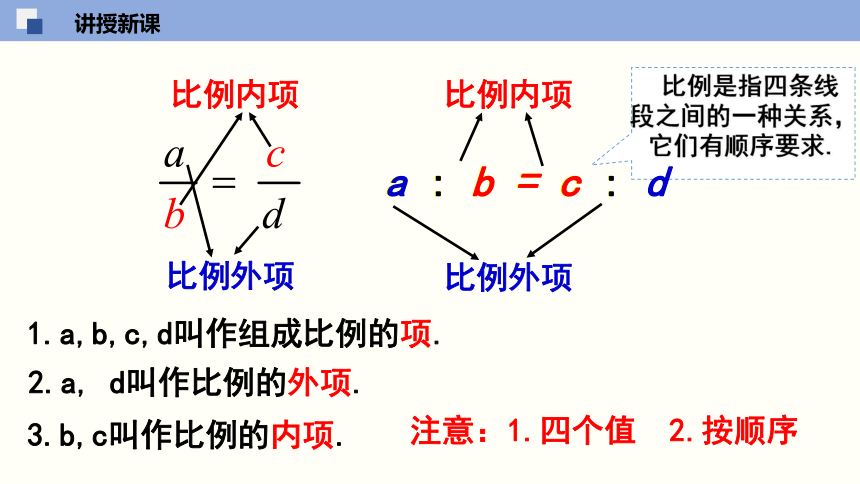
1.a,b,c,d叫作组成比例的项.
2.a, d叫作比例的外项.
3.b,c叫作比例的内项.
注意:1.四个值 2.按顺序
a : b = c :
比例内项
比例外项
比例是指四条线段之间的一种关系,它们有顺序要求.
a : b = c : d
比例内项
比例外项
讲授新课
1、在四条线段中,如果两条线段的比等于另两条线段的比,
那么这四条线段叫做成比例线段,简称比例线段
注意:四条线段成比例时,要把这四条线段按顺序排列,不能随意颠倒
2、比例:两个比相等的式子叫做比例,如 a:b=c:d
(1)比例的四个项a、b、c、d分别叫做第一、二、三、四比例项
(2)其中a和d又叫做比例外项,b和c叫做比例内项
(3)在比例式a:b=b:c中,b叫做a和c的比例中项?
讲授新课
3、判断四条线段是否是成比例线段的方法:
(1)单位统一——确保四条线段的单位统一
(2)排序——将线段按照从小到大的顺序排列
(3)计算——分别计算排序后的前两条线段的比、后两条线段的比
(4)看——看比是否相等
讲授新课
典例精析
【例2】下列各组中的四条线段成比例的是( )
A.1cm,2cm,3cm,4cm B.1cm,2cm,20cm,40cm
C.4cm,2cm,5cm,3cm D.5cm,10cm,15cm,20cm
【分析】
A.1×4≠2×3,∴四条线段不成比例;
B.1×40=2×20,∴四条线段成比例;
C.排序:2cm,3cm,4cm,5cm,2×5≠3×4,∴四条线段不成比例;
D.5×20≠10×15,∴四条线段不成比例.
B
讲授新课
练一练
1、线段a=2cm,b=3cm,c=lcm,那么a、b、c的第四比例项d=________.
2、线段a=6cm,b=2cm,则a、b、a+b的第四比例项是________cm.
【分析5-1】
∵????????=????????,
∴????????????????????????=????????????????,
∴d=1.5cm
?
【分析5-2】
设第四比例项为d
∵????????=????+????????,
∴????????????????????????=????????????????,
∴d=????????cm
?
【注意】单位不能漏
1.5cm
????????
?
讲授新课
知识点三 比例的基本性质
1.如果
,那么ad=bc.
2.如果ad=bc(a、b、c、d都不等于0),那么 .
两外项之积=两内项之积。
左 右
右 左
交叉相乘积相等
右 左
左 右
讲授新课
如果作为比例内项的两条线段是相等的,即 (或 a:b=b:c),那么线段b叫线段a,c的比例中项。。
特别地,
三种不同形式:
a:b=b:c
b2=ac
讲授新课
思考:你发现了什么?
探究等比性质,先独立完成,再与同伴交流
讲授新课
等比性质
讲授新课
典例精析
【例3】若a=4cm,b=9cm,则线段a,b的比例中项是________cm.
【分析】
设比例中项为m
∵ab=m2,
∴(4cm)×(9cm)=m2,
∵m>0
∴m=6cm
讲授新课
练一练
1、已知三个数3、6、x,要使其中一个数是其他两数的比例中项,则x的取值是____________________________.
【分析】比例中项指代不明,需分类讨论
①设3为比例中项,则6x=32,解得:x=????????;
②设6为比例中项,则3x=62,解得:x=12;
③设x为比例中项,则3×6=x2,解得:x=±????????;
综上,x=????????或x=12或x=±????????
?
x=????????或x=12或x=±????????
?
讲授新课
2、若a:b=3:4,b:c=1:2,则a:c=________.
【分析】
∵a:b=3:4,b:c=1:2=4:8,
∴a:b:c=3:4:8,
∴a:c=3:8
【总结】
本题方法:把b转化成同一个数,进行连比
讲授新课
3、已知????????=????????,那么?????????????=________.
?
【分析】
∵????????=????????,
∴????????-1=????????-1,即?????????????=-????????,
∴?????????????=????????
?
????????
?
讲授新课
4、已知????????=????????,那么????+?????????????=________.
?
【分析】法一:
∵????????=????????,
∴a=????????b,
∴????+?????????????=????+?????????????????????????????=????????????????????????=4
?
4
法二:
∵????????=????????,
∴设a=3k,b=5k,
∴????+?????????????=????????+?????????????????????????=????????????????=4
?
【对比总结】
设“k”法更简单明了
讲授新课
5、已知a:b:c=9:11:14,且a+b+c=68,则3a-2b+c=________.
【分析】
∵a:b:c=9:11:14,且a+b+c=68,
∴设a=9k,b=11k,c=14k,
∴9k+11k+14k=68,解得:k=2,
∴a=18,b=22,c=28,
∴3a-2b+c=38
讲授新课
6、已知????????=????????=????????=????????,且b+d+f≠0,则????+????+????????+????+????=________.
?
【分析】
∵????????=????????=????????=????????,且b+d+f≠0,
∴根据等比定理:????+????+????????+????+????=????????
?
????????
?
讲授新课
知识点四 黄金分割
●
C
B
A
解析:①由比例式可得AC=AB·BC,即当图中的较长线段AC是最长线段AB和最短线段BC的比例中项时,点C为线段AB的黄金分割点.
●
●
讲授新课
解析:②若设AB为1,AC为x,则x是1和(1-x)的比例中项.由前边“巩固练习”可知,x= .
●
C
B
A
●
●
③线段AB有两个黄金分割点,一个靠近端点A,一个靠近端点B.
讲授新课
议一议:“黄金分割”在生活中还有哪些应用呢?
一片树叶也蕴含着“黄金分割”
鹦鹉螺外壳,其每圈螺纹的直径与相邻螺纹直径的比约为0.618
讲授新课
议一议:已知AC的长度,点B为线段AC的黄金分割点,求AB的长度
①AB1∵点B为线段AC的黄金分割点
∴????????????????=?????????????
∴????????????????=?????????????????????????=1-????????????????=1-?????????????=?????????????
∴AB=(1-?????????????)AC=?????????????AC
?
A
C
B1
B2
②AB2>BC2
∵点B为线段AC的黄金分割点
∴????????????????=?????????????
∴AB=?????????????AC
?
【分析】
B点有两种可能性,需分类讨论
讲授新课
【题型:求线段的长】
已知AC的长度,点B为线段AC的黄金分割点,求AB的长度
①ABBC时AB=?????????????AC
?
讲授新课
典例精析
【例4】在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
解:设肚脐到脚底的距离为 x m,根据题意,得 ,解得x = 0.96.
设穿上 y m高的高跟鞋看起来会更美,则
解得 y≈0.075,而0.075m=7.5cm.
故她应该穿约为7.5cm高的高跟鞋看起来会更美.
讲授新课
练一练
1、已知点P是线段AB的黄金分割点(AP>PB),AB=6,那么AP的长是____________cm.
【分析】
∵点P是线段AB的黄金分割点(AP>PB)
∴AP=?????????????AB=?????????????×6=3????-3
?
3????-3
?
讲授新课
2、如果一个矩形的宽(即短边)与长(即长边)之比是?????????????,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E、F、G、H分别为线段AD、BC、AB、EF的中点,则图中黄金矩形共有________个.
?
【分析】
∵矩形ABCD是黄金矩形,点E、F、G、H分别为线段AD、BC、AB、EF的中点,
∴黄金矩形还有矩形AEGH,矩形GHFB,
∴图中黄金矩形共有3个
3
讲授新课
3、如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是________个.
(1)????????????????=????????????????;
(2)AB:AP=AP:PB;
(3)BP2=AP·AB;
(4)????????????????≈0.618.
?
【分析】
∵P为线段AB的黄金分割点,且AP>BP,
∴????????????????=???????????????? ,即????????????????=????????????????,AP2=BP·AB,
∴(1)正确;(2)正确;(3)错误;
∵黄金比为0.618,
∴??????????????≈0.618,(4)正确.
?
3
课堂小结
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比。
其中,线段AB,CD分别叫做这个线段比的前项和后项。
1.线段的比
课堂小结
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即:
2.成比例线段的概念
那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
课堂小结
1.a,b,c,d叫作组成比例的项.
2.a, d叫作比例的外项.
3.b,c叫作比例的内项.
a : b = c :
比例内项
比例外项
比例是指四条线段之间的一种关系,它们有顺序要求。
a : b = c : d
比例内项
比例外项
课堂小结
1.如果
,那么ad=bc.
2.如果ad=bc(a、b、c、d都不等于0),那么 .
两外项之积=两内项之积.
左 右
右 左
交叉相乘积相等
右 左
左 右
3.比例的基本性质
课堂小结
黄金分割
点C把线段AB分成两条线段AC和BC,如果 , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
黄金分割点:一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
定义
谢 谢~
数学(浙教版)
九年级 上册
第4章 相似三角形
学习目标
1、理解并掌握线段的比、成比例线段的概念和相关组成元素;
2、理解并能灵活运用比例的基本性质解决问题;
3、掌握黄金分割的相关概念与应用;
导入新课
问题:两组图中A、B之间有何关系?
A B
【分析】形状相同、大小相等——全等
导入新课
问题:两组图中A、B之间有何关系?
A B
A B
【分析】形状相同、但是大小不等
讲授新课
知识点一 线段的比
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比.
其中,线段AB,CD分别叫做这个线段比的前项和后项.
讲授新课
设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,AD, EF, EH的长度分别是多少?
四条线段a, b, c, d中,如果a与b的比等于c与d的比,即 ,那么这四条线段a , b ,c , d叫作成比例线段,简称比例线段.
A
B
C
D
G
H
E
F
讲授新课
典例精析
【例1】已知AB长为1dm,CD长为2cm,则AB:CD=________.
【分析】
∵AB=1dm=10cm
∴AB:CD=10:2=5:1
【总结】
(1)计算线段的比,即计算线段长度的比
(2)需保证长度的单位统一
讲授新课
1.已知教室黑板的长 a = 3.2 m,宽 b = 120 cm ,求 a:b。
∴a :b = 320 :120 = 8 :3
或:
2.一条线段的长度是另一条线段长度的 ,则这两条线段之比是?
∵a=3.2m=320cm
练一练
讲授新课
知识点二 成比例线段的概念
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即:
那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
讲授新课
1.a,b,c,d叫作组成比例的项.
2.a, d叫作比例的外项.
3.b,c叫作比例的内项.
注意:1.四个值 2.按顺序
a : b = c :
比例内项
比例外项
比例是指四条线段之间的一种关系,它们有顺序要求.
a : b = c : d
比例内项
比例外项
讲授新课
1、在四条线段中,如果两条线段的比等于另两条线段的比,
那么这四条线段叫做成比例线段,简称比例线段
注意:四条线段成比例时,要把这四条线段按顺序排列,不能随意颠倒
2、比例:两个比相等的式子叫做比例,如 a:b=c:d
(1)比例的四个项a、b、c、d分别叫做第一、二、三、四比例项
(2)其中a和d又叫做比例外项,b和c叫做比例内项
(3)在比例式a:b=b:c中,b叫做a和c的比例中项?
讲授新课
3、判断四条线段是否是成比例线段的方法:
(1)单位统一——确保四条线段的单位统一
(2)排序——将线段按照从小到大的顺序排列
(3)计算——分别计算排序后的前两条线段的比、后两条线段的比
(4)看——看比是否相等
讲授新课
典例精析
【例2】下列各组中的四条线段成比例的是( )
A.1cm,2cm,3cm,4cm B.1cm,2cm,20cm,40cm
C.4cm,2cm,5cm,3cm D.5cm,10cm,15cm,20cm
【分析】
A.1×4≠2×3,∴四条线段不成比例;
B.1×40=2×20,∴四条线段成比例;
C.排序:2cm,3cm,4cm,5cm,2×5≠3×4,∴四条线段不成比例;
D.5×20≠10×15,∴四条线段不成比例.
B
讲授新课
练一练
1、线段a=2cm,b=3cm,c=lcm,那么a、b、c的第四比例项d=________.
2、线段a=6cm,b=2cm,则a、b、a+b的第四比例项是________cm.
【分析5-1】
∵????????=????????,
∴????????????????????????=????????????????,
∴d=1.5cm
?
【分析5-2】
设第四比例项为d
∵????????=????+????????,
∴????????????????????????=????????????????,
∴d=????????cm
?
【注意】单位不能漏
1.5cm
????????
?
讲授新课
知识点三 比例的基本性质
1.如果
,那么ad=bc.
2.如果ad=bc(a、b、c、d都不等于0),那么 .
两外项之积=两内项之积。
左 右
右 左
交叉相乘积相等
右 左
左 右
讲授新课
如果作为比例内项的两条线段是相等的,即 (或 a:b=b:c),那么线段b叫线段a,c的比例中项。。
特别地,
三种不同形式:
a:b=b:c
b2=ac
讲授新课
思考:你发现了什么?
探究等比性质,先独立完成,再与同伴交流
讲授新课
等比性质
讲授新课
典例精析
【例3】若a=4cm,b=9cm,则线段a,b的比例中项是________cm.
【分析】
设比例中项为m
∵ab=m2,
∴(4cm)×(9cm)=m2,
∵m>0
∴m=6cm
讲授新课
练一练
1、已知三个数3、6、x,要使其中一个数是其他两数的比例中项,则x的取值是____________________________.
【分析】比例中项指代不明,需分类讨论
①设3为比例中项,则6x=32,解得:x=????????;
②设6为比例中项,则3x=62,解得:x=12;
③设x为比例中项,则3×6=x2,解得:x=±????????;
综上,x=????????或x=12或x=±????????
?
x=????????或x=12或x=±????????
?
讲授新课
2、若a:b=3:4,b:c=1:2,则a:c=________.
【分析】
∵a:b=3:4,b:c=1:2=4:8,
∴a:b:c=3:4:8,
∴a:c=3:8
【总结】
本题方法:把b转化成同一个数,进行连比
讲授新课
3、已知????????=????????,那么?????????????=________.
?
【分析】
∵????????=????????,
∴????????-1=????????-1,即?????????????=-????????,
∴?????????????=????????
?
????????
?
讲授新课
4、已知????????=????????,那么????+?????????????=________.
?
【分析】法一:
∵????????=????????,
∴a=????????b,
∴????+?????????????=????+?????????????????????????????=????????????????????????=4
?
4
法二:
∵????????=????????,
∴设a=3k,b=5k,
∴????+?????????????=????????+?????????????????????????=????????????????=4
?
【对比总结】
设“k”法更简单明了
讲授新课
5、已知a:b:c=9:11:14,且a+b+c=68,则3a-2b+c=________.
【分析】
∵a:b:c=9:11:14,且a+b+c=68,
∴设a=9k,b=11k,c=14k,
∴9k+11k+14k=68,解得:k=2,
∴a=18,b=22,c=28,
∴3a-2b+c=38
讲授新课
6、已知????????=????????=????????=????????,且b+d+f≠0,则????+????+????????+????+????=________.
?
【分析】
∵????????=????????=????????=????????,且b+d+f≠0,
∴根据等比定理:????+????+????????+????+????=????????
?
????????
?
讲授新课
知识点四 黄金分割
●
C
B
A
解析:①由比例式可得AC=AB·BC,即当图中的较长线段AC是最长线段AB和最短线段BC的比例中项时,点C为线段AB的黄金分割点.
●
●
讲授新课
解析:②若设AB为1,AC为x,则x是1和(1-x)的比例中项.由前边“巩固练习”可知,x= .
●
C
B
A
●
●
③线段AB有两个黄金分割点,一个靠近端点A,一个靠近端点B.
讲授新课
议一议:“黄金分割”在生活中还有哪些应用呢?
一片树叶也蕴含着“黄金分割”
鹦鹉螺外壳,其每圈螺纹的直径与相邻螺纹直径的比约为0.618
讲授新课
议一议:已知AC的长度,点B为线段AC的黄金分割点,求AB的长度
①AB1
∴????????????????=?????????????
∴????????????????=?????????????????????????=1-????????????????=1-?????????????=?????????????
∴AB=(1-?????????????)AC=?????????????AC
?
A
C
B1
B2
②AB2>BC2
∵点B为线段AC的黄金分割点
∴????????????????=?????????????
∴AB=?????????????AC
?
【分析】
B点有两种可能性,需分类讨论
讲授新课
【题型:求线段的长】
已知AC的长度,点B为线段AC的黄金分割点,求AB的长度
①AB
?
讲授新课
典例精析
【例4】在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
解:设肚脐到脚底的距离为 x m,根据题意,得 ,解得x = 0.96.
设穿上 y m高的高跟鞋看起来会更美,则
解得 y≈0.075,而0.075m=7.5cm.
故她应该穿约为7.5cm高的高跟鞋看起来会更美.
讲授新课
练一练
1、已知点P是线段AB的黄金分割点(AP>PB),AB=6,那么AP的长是____________cm.
【分析】
∵点P是线段AB的黄金分割点(AP>PB)
∴AP=?????????????AB=?????????????×6=3????-3
?
3????-3
?
讲授新课
2、如果一个矩形的宽(即短边)与长(即长边)之比是?????????????,那么这个矩形称为黄金矩形.如图,矩形ABCD是黄金矩形,点E、F、G、H分别为线段AD、BC、AB、EF的中点,则图中黄金矩形共有________个.
?
【分析】
∵矩形ABCD是黄金矩形,点E、F、G、H分别为线段AD、BC、AB、EF的中点,
∴黄金矩形还有矩形AEGH,矩形GHFB,
∴图中黄金矩形共有3个
3
讲授新课
3、如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是________个.
(1)????????????????=????????????????;
(2)AB:AP=AP:PB;
(3)BP2=AP·AB;
(4)????????????????≈0.618.
?
【分析】
∵P为线段AB的黄金分割点,且AP>BP,
∴????????????????=???????????????? ,即????????????????=????????????????,AP2=BP·AB,
∴(1)正确;(2)正确;(3)错误;
∵黄金比为0.618,
∴??????????????≈0.618,(4)正确.
?
3
课堂小结
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比。
其中,线段AB,CD分别叫做这个线段比的前项和后项。
1.线段的比
课堂小结
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即:
2.成比例线段的概念
那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
课堂小结
1.a,b,c,d叫作组成比例的项.
2.a, d叫作比例的外项.
3.b,c叫作比例的内项.
a : b = c :
比例内项
比例外项
比例是指四条线段之间的一种关系,它们有顺序要求。
a : b = c : d
比例内项
比例外项
课堂小结
1.如果
,那么ad=bc.
2.如果ad=bc(a、b、c、d都不等于0),那么 .
两外项之积=两内项之积.
左 右
右 左
交叉相乘积相等
右 左
左 右
3.比例的基本性质
课堂小结
黄金分割
点C把线段AB分成两条线段AC和BC,如果 , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
黄金分割点:一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
定义
谢 谢~
同课章节目录
