2014年第3章实数 单元练习卷(学生 教师分卷)
文档属性
| 名称 | 2014年第3章实数 单元练习卷(学生 教师分卷) |  | |
| 格式 | zip | ||
| 文件大小 | 120.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-16 11:03:42 | ||
图片预览


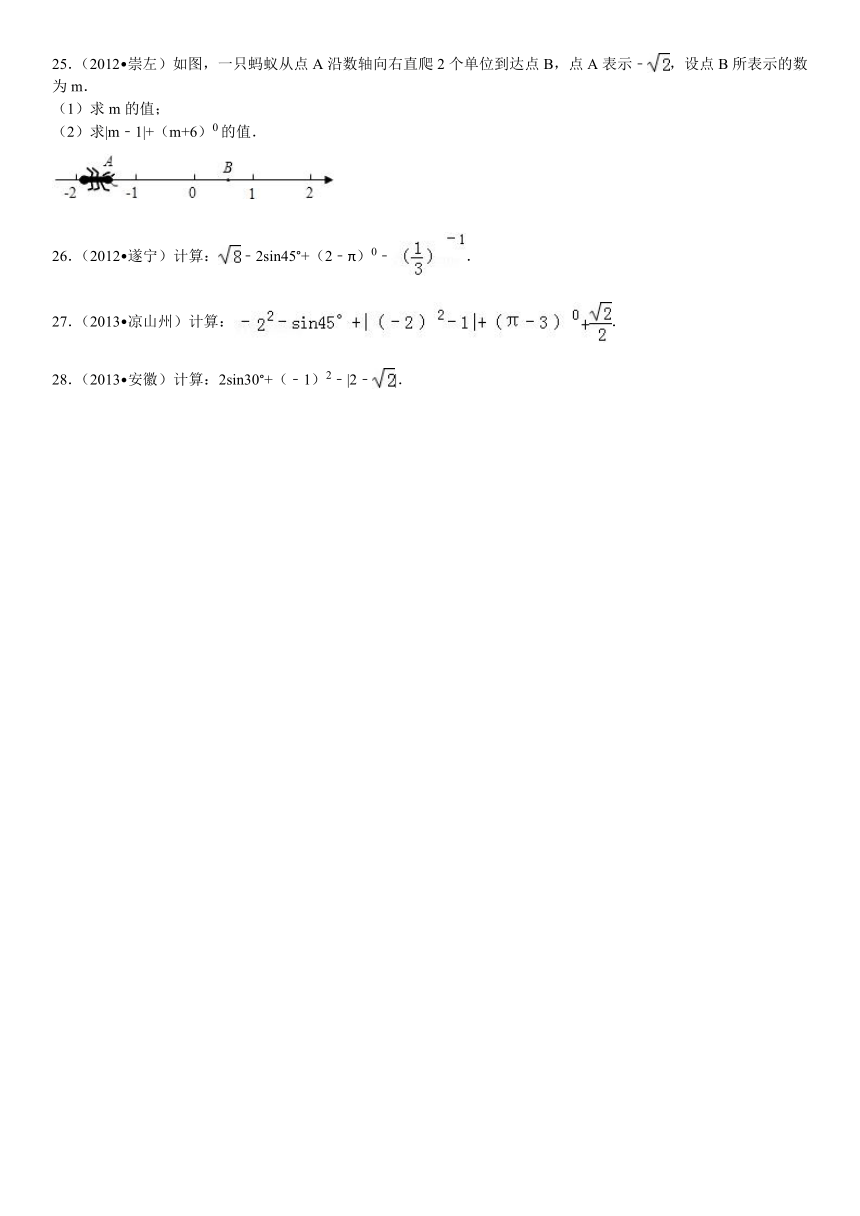


文档简介
第3章 实数
一、选择题(共10小题)
1.(2011 黔南州)有一个数值转换器,原理如下:当输入的x=64时,输出的y等于( )
( http: / / www.21cnjy.com )
A. 2 B. 8 C. D.
2.(2010 淮安)下面四个数中与最接近的数是( )
A. 2 B. 3 C. 4 D. 5
3.(2010 天津)比较2,,的大小,正确的是( )
A. B. C. D.
4.(2009 邵阳)与最接近的整数是( )
A. 0 B. 2 C. 4 D. 5
5.(2010 怀化)若0<x<1,则x,x2,x3的大小关系是( )
A. x<x2<x3 B. x<x3<x2 C. x3<x2<x D. x2<x3<x
6.(2010 金华)如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A. a<1<﹣a B. a<﹣a<1 C. 1<﹣a<a D. ﹣a<a<1
7.(2008 盐城)实数a在数轴上对应的点如图所示,则a,﹣a,1的大小关系正确的是( )
A. ﹣a<a<1 B. a<﹣a<1 C. 1<﹣a<a D. a<1<﹣a
8.(2008 北京)若|x+2|+,则xy的值为( )
A. ﹣8 B. ﹣6 C. 5 D. 6
9.(2013 永州)我们知道,一元二次 ( http: / / www.21cnjy.com )方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n i=(i4)n i=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为( )
A. 0 B. 1 C. ﹣1 D. i
10.(2012 湘潭)文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,若输入,则输出的结果为( )
A. 5 B. 6 C. 7 D. 8
二、填空题(共8小题)(除非特别说明,请填准确值)
11.(2013 湘潭)计算:= _________ .
12.(2012 东莞)若x,y为实数,且满足|x﹣3|+=0,则的值是 _________ .
13.(2013 台州)任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[]=1.现对72进行如下操作:72[]=8[]=2[]=1,这样对72只需进行3次操作后变为1,类似的,①对81只需进行 _________ 此操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 _________ .
14.(2012 汕头)若x,y为实数,且满足|x﹣3|+=0,则()2012的值是 _________ .
15.(2012 张家界)已知,则x+y= _________ .
16.(2012 常德)规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3.按此规定[]的值为 _________ .
17.(2012 南平)设[x)表示大于x的最小整数,如[3)=4,[﹣1.2)=﹣1,
则下列结论中正确的是 _________ .(填写所有正确结论的序号)
①[0)=0;②[x)﹣x的最小值是0;③[x)﹣x的最大值是0;④存在实数x,使[x)﹣x=0.5成立.
18.(2011 内江)已知|6﹣3m|+(n﹣5)2=3m﹣6﹣,则m﹣n= _________
三、解答题(共10小题)(选答题,不自动判卷)
19.(2013 常德)计算;(π﹣2)0++(﹣1)2013﹣()﹣2.
20.(2013 南宁)计算:20130﹣+2cos60°+(﹣2)
21.(2012 眉山)计算:4cos30°+()﹣2﹣(﹣1)
22.(2013 长沙)计算:.
23.(2013 重庆)计算:(﹣3)0﹣﹣(﹣1)2013﹣|﹣2|+(﹣)﹣2.
24.(2013 重庆)计算:.
25.(2012 崇左)如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣,设点B所表示的数为m.
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值.
26.(2012 遂宁)计算:﹣2sin45°+(2﹣π)0﹣.
27.(2013 凉山州)计算:.
28.(2013 安徽)计算:2sin30°+(﹣1)2﹣|2﹣|.
第3章 实数(教师讲评卷)
一、选择题(共10小题)
1.(2011 黔南州)有一个数值转换器,原理如下:当输入的x=64时,输出的y等于( )
( http: / / www.21cnjy.com )
A. 2 B. 8 C. D.
考点: 算术平方根.
专题: 压轴题;图表型.
分析: 根据图中的步骤,把64输入,可得其算术平方根为8,8再输入得其算术平方根是,是无理数则输出.
解答: 解:由图表得,64的算术平方根是8,8的算术平方根是;故选D.
点评: 本题考查了算术平方根的定义,看懂图表的原理是正确解答的关键.
2.(2010 淮安)下面四个数中与最接近的数是( )
A. 2 B. 3 C. 4 D. 5
考点: 估算无理数的大小.
分析: 先根据的平方是11,距离11最近的完全平方数是9和16,通过比较可知11距离9比较近,由此即可求解.
解答: 解:∵32=9,3.52=12.25,42=16∴<<<,∴与最接近的数是3,而非4.故选B.
点评: 此题主要考查了无理数的估算能力,通过比较二次根式的平方的大小来比较二次根式的大小是常用的一种比较方法和估算方法.
3.(2010 天津)比较2,,的大小,正确的是( )
A. B. C. D.
考点: 实数大小比较.
专题: 应用题.
分析: 首先把各数同时立方,然后比较被开方数的大小,即可解决问题.
解答: 解:∵23=8,()3=5≈11.2,()3=7∴<2<.故选C.
点评: 此题主要考查了实数大小的比较,本题可通过比较它们的立方来比较大小.
4.(2009 邵阳)与最接近的整数是( )
A. 0 B. 2 C. 4 D. 5
考点: 估算无理数的大小.
专题: 压轴题.
分析: 先估计的近似值,然后判断与最接近的整数即可求解.
解答: 解:∵1<3<4,∴1<<2.故选B
点评: 此题主要考查了正确根据平方进行估算的能力,现实生活中经常需要估算,估算应是我们具备的数学能力,“夹逼法”是估算的一般方法,也是常用方法.
5.(2010 怀化)若0<x<1,则x,x2,x3的大小关系是( )
A. x<x2<x3 B. x<x3<x2 C. x3<x2<x D. x2<x3<x
考点: 实数大小比较.
专题: 压轴题.
分析: 首先根据条件给出符合条件的具体数值,然后根据负数小于一切正数,两个负数比较大小,两个负数绝对值大的反而小即可解答.
解答: 解:∵0<x<1,∴假设x=,则x=,x2=,x3=,∵<<,∴x3<x2<x.故选C.
点评: 此题主要考查了实数的大小的比较,解答此题的关键是根据条件设出符合条件的具体数值,再即可方便比较大小.
6.(2010 金华)如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A. a<1<﹣a B. a<﹣a<1 C. 1<﹣a<a D. ﹣a<a<1
考点: 实数与数轴.
分析: 根据数轴可以得到a<1<﹣a,据此即可确定哪个选项正确.
解答: 解:∵实数a在数轴上原点的左边,∴a<0,但|a|>1,﹣a>1,则有a<1<﹣a.故选A.
点评: 本题考查了实数与数轴的对应关系,数轴上的数右边的数总是大于左边的数
7.(2008 盐城)实数a在数轴上对应的点如图所示,则a,﹣a,1的大小关系正确的是( )
A. ﹣a<a<1 B. a<﹣a<1 C. 1<﹣a<a D. a<1<﹣a
考点: 实数与数轴;实数大小比较.
专题: 压轴题.
分析: 本题首先运用数形结合的思想确定a的正负情况,然后根据相反数意义即可解题.
解答: 解:由数轴上a的位置可知a<0,|a|>1;设a=﹣2,则﹣a=2,∵﹣2<1<2∴a<1<﹣a,故选项A,B,C错误,选项D正确.故选D.
点评: 此题主要考查了比较实数的大小,解答此题的关键是根据数轴上a的位置估算出a的值,设出符合条件的数值,再比较大小即可.
8.(2008 北京)若|x+2|+,则xy的值为( )
A. ﹣8 B. ﹣6 C. 5 D. 6
考点: 非负数的性质:算术平方根;非负数的性质:绝对值.
专题: 压轴题.
分析: 已知任何数的绝对值一定是非负数,二次根式的 ( http: / / www.21cnjy.com )值一定是一个非负数,由于已知的两个非负数的和是0,根据非负数的性质得到这两个非负数一定都是0,从而得到一个关于x、y的方程组,解方程组就可以得到x、y的值,进而求出xy的值.
解答: 解:∵|x+2|≥0,≥0,而|x+2|+=0,∴x+2=0且y﹣3=0,∴x=﹣2,y=3,∴xy=(﹣2)×3=﹣6.故选:B.
点评: 本题考查的是非负数的性质,一元一次方程的解法及代数式的求值.题目注重基础,比较简单.
9.(2013 永州)我们知道,一元二次方 ( http: / / www.21cnjy.com )程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n i=(i4)n i=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为( )
A. 0 B. 1 C. ﹣1 D. i
考点: 实数的运算.
专题: 压轴题;新定义.
分析: i1=i,i2=﹣1,i3 ( http: / / www.21cnjy.com )=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,i5=i4 i=i,i6=i5 i=﹣1,从而可得4次一循环,一个循环内的和为0,计算即可.
解答: 解:由题意得,i1=i,i2=﹣1,i ( http: / / www.21cnjy.com )3=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,i5=i4 i=i,i6=i5 i=﹣1,故可发现4次一循环,一个循环内的和为0,∵=503…1,∴i+i2+i3+i4+…+i2012+i2013=i.故选D.
点评: 本题考查了实数的运算,解答本题的关键是计算出前面几个数的值,发现规律,求出一个循环内的和再计算,有一定难度.
10.(2012 湘潭)文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,若输入,则输出的结果为( )
A. 5 B. 6 C. 7 D. 8
考点: 实数的运算.
专题: 压轴题.
分析: 根据运算程序得出输出数的式子,再根据实数的运算计算出此数即可.
解答: 解:∵输入一个数后,输出的数比输入的数的平方小1,∴输入,则输出的结果为()2﹣1=7﹣1=6.故选B.
点评: 本题考查的是实数的运算,根据题意得出输出数的式子是解答此题的关键.
二、填空题(共8小题)(除非特别说明,请填准确值)
11.(2013 湘潭)计算:= 2 .
考点: 实数的运算;零指数幂;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 本题涉及零指数幂、特殊角的三角函数值、二次根式化简等考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式=×+1=1+1=2.故答案为2.
点评: 本题考查实数的综合运算能力,是各地 ( http: / / www.21cnjy.com )中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握零指数幂、特殊角的三角函数值、二次根式化简等考点的运算.
12.(2012 东莞)若x,y为实数,且满足|x﹣3|+=0,则的值是 1 .
考点: 非负数的性质:算术平方根;非负数的性质:绝对值.
专题: 压轴题.
分析: 根据非负数的性质列式求出x、y的值,再代入代数式进行计算即可得解.
解答: 解:根据题意得,x﹣3=0,y+3=0,解得x=3,y=﹣3,所以,()2012=()2012=1.故答案为:1.
点评: 本题考查了绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.
13.(2013 台州)任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[]=1.现对72进行如下操作:72[]=8[]=2[]=1,这样对72只需进行3次操作后变为1,类似的,①对81只需进行 3 此操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 255 .
考点: 估算无理数的大小.
专题: 压轴题;新定义.
分析: ①根据规律依次求出即可;②要想确 ( http: / / www.21cnjy.com )定只需进行3次操作后变为1的所有正整数,关键是确定二次操作后数的大小不能大于4,二次操作时根号内的数必须小于16,而一次操作时正整数255却好满足这一条件,即最大的正整数为255.
解答: 解:①[]=9,[]=3,[]=1,故答案为:3;②最大的是255,[]=15,[]=3,[]=1,而[]=16,[]=4,[]=2,[]=1,即只需进行3次操作后变为1的所有正整数中,最大的正整数是255,故答案为:255.
点评: 本题考查了估算无理数的大小的应用,主要考查学生的阅读能力和猜想能力.
14.(2012 汕头)若x,y为实数,且满足|x﹣3|+=0,则()2012的值是 1 .
考点: 非负数的性质:算术平方根;非负数的性质:绝对值.
分析: 根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可
解答: 解:根据题意得:,解得:.则()2012=()2012=1.故答案是:1.
点评: 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
15.(2012 张家界)已知,则x+y= 1 .
考点: 非负数的性质:算术平方根;非负数的性质:偶次方.
专题: 计算题;压轴题.
分析: 根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.
解答: 解:∵,∴,解得,则x+y=﹣1+2=1,故答案为1.
点评: 本题考查了非负数的性质,利用该性质建立关于x、y的方程组是解题的关键.
16.(2012 常德)规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3.按此规定[]的值为 4 .
考点: 估算无理数的大小.
专题: 压轴题;新定义.
分析: 求出的范围,求出+1的范围,即可求出答案.
解答: 解:∵3<<4,∴3+1<+1<4+1,∴4<+1<5,∴[+1]=4,故答案为:4.
点评: 本题考查了估计无理数的应用,关键是确定+1的范围,题目比较新颖,是一道比较好的题目.
17.(2012 南平)设[x)表示大于x的最小整数,如[3)=4,[﹣1.2)=﹣1,
则下列结论中正确的是 ④ .(填写所有正确结论的序号)
①[0)=0;②[x)﹣x的最小值是0;③[x)﹣x的最大值是0;④存在实数x,使[x)﹣x=0.5成立.
考点: 实数的运算.
专题: 压轴题;新定义.
分析: 根据题意[x)表示大于x的最小整数,结合各项进行判断即可得出答案.
解答: 解:①[0)=1,故本项错误;②[x)﹣x>0,但是取不到0,故本项错误;③[x)﹣x≤1,即最大值为1,故本项错误;④存在实数x,使[x)﹣x=0.5成立,例如x=0.5时,故本项正确.故答案为④.
点评: 此题考查了实数的运算,仔细审题,理解[x)表示大于x的最小整数是解答本题的关键,难度一般.
18.(2011 内江)已知|6﹣3m|+(n﹣5)2=3m﹣6﹣,则m﹣n= ﹣2
考点: 非负数的性质:算术平方根;非负数的性质:绝对值;非负数的性质:偶次方.
分析: 根据|6﹣3m|+(n﹣5)2=3m﹣6﹣,得出6﹣3m≤0,将已知等式化简,可得n﹣5=0,以及m﹣3=0,即可求出n,m的值,即可得出答案.
解答: 解:∵|6﹣3m|+(n﹣5)2=3m﹣6﹣,∴6﹣3m≤0,m﹣3≥0,∴m≥3,∴已知等式化简,得(n﹣5)2=﹣,∴(n﹣5)2+=0,∴n﹣5=0,n=5,∴m﹣3=0,m=3,则m﹣n=3﹣5=﹣2.故答案为:﹣2.
点评: 此题主要考查了算术平方根以及绝对值的性质,根据题意得出n,m的值是解决问题的关键.
三、解答题(共10小题)(选答题,不自动判卷)
19.(2013 常德)
考点: 实数的运算;零指数幂;负整数指数幂.
专题: 压轴题.
分析: 分别进行零指数幂、负整数指数幂及二次根式的化简,然后合并可得出答案.
解答: 解:
点评: 本题考查了实数的运算,涉及了零指数幂、负整数指数幂的运算,解答本题的关键是掌握各部分的运算法则.
20.(2013 南宁)计算:20130﹣+2cos60°+(﹣2)
考点: 实数的运算;零指数幂;特殊角的三角函数值.
专题: 压轴题.
分析: 分别进行零指数幂、二次根式的化简,然后代入特殊角的三角函数值合并即可得出答案.
解答: 解:原式=1﹣3+2×﹣2=﹣3.
点评: 本题考查了实数的运算,属于基础题,关键是掌握零指数幂的运算法则及一些特殊角的三角函数值.
21.(2012 眉山)计算:4cos30°+()﹣2﹣(﹣1)
考点: 实数的运算;负整数指数幂;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 根据负整数指数幂的意义和cos30°=得到原式=4×+4﹣2+1,再进行乘法运算,然后合并即可.
解答: 解:原式=4×+4﹣2+1=2+4﹣2+1=5.
点评: 本题考查了实数的运算:先进行乘法运算,再进行乘除运算,然后进行加减运算;有括号先算括号.也考查了负整数指数幂与特殊角的三角函数值.
22.(2013 长沙)计算:.
考点: 实数的运算;零指数幂.
专题: 压轴题.
分析: 分别进行绝对值、平方及零指数幂的运算,然后合并即可得出答案.
解答: 解:原式=3+4﹣1=6.
点评: 本题考查了实数的运算,属于基础题,掌握各部分的运算法则 是关键.
23.(2013 重庆)计算:(﹣3)0﹣﹣(﹣1)2013﹣|﹣2|+(﹣)﹣2.
考点: 实数的运算;零指数幂;负整数指数幂.
专题: 计算题;压轴题.
分析: 原式第一项利用零指数幂法则计算,第二项利用平 ( http: / / www.21cnjy.com )方根的定义化简,第三项表示2013个﹣1的乘积,第四项利用负数的绝对值等于它的相反数计算,最后一项利用负指数幂法则计算即可得到结果.
解答: 解:原式=1﹣3+1﹣2+9=6.
点评: 此题考查了实数的运算,涉及的知识有:零指数、负指数幂,平方根的定义,绝对值的代数意义,熟练掌握运算法则是解本题的关键.
24.(2013 重庆)计算:.
考点: 实数的运算;零指数幂;负整数指数幂.
专题: 压轴题.
分析: 分别进行乘方、绝对值、零指数幂、开立方等运算,然后按照实数的运算法则计算即可.
解答: 解:原式=﹣1﹣2+1×2+4=3.
点评: 本题考查了实数的运算,涉及了乘方、绝对值、零指数幂、开立方等知识,属于基础题.
25.(2012 崇左)如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣,设点B所表示的数为m.
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值.
考点: 实数与数轴;零指数幂.
专题: 图表型.
分析: (1)根据正负数的意义计算;(2)根据绝对值的意义和零指数幂的运算法则计算.
解答: 解:(1)由题意A点和B点的距离为2,其A点的坐标为﹣,因此B点坐标m=2﹣.(2)把m的值代入得:|m﹣1|+(m+6)0=|2﹣﹣1|+(2﹣+6)0,=|1﹣|+(8﹣)0,=﹣1+1,=.
点评: 本题考查了含有零指数幂的运算,任何非0数的0次幂等于1,还要注意去绝对值符号时,结果为非负数.
26.(2012 遂宁)计算:﹣2sin45°+(2﹣π)0﹣.
考点: 实数的运算;零指数幂;负整数指数幂;二次根式的性质与化简;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 本题涉及零指数幂、负整数指 ( http: / / www.21cnjy.com )数幂、特殊角的三角函数值、二次根式化简四个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式==.
点评: 本题考查实数的运算能力, ( http: / / www.21cnjy.com )解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式等考点的运算.注意:负指数为正指数的倒数;任何非0数的0次幂等于1;二次根式的化简是根号下不能含有分母和能开方的数.
27.(2013 凉山州)计算:.
考点: 实数的运算;零指数幂;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 原式第一项表示2平方的相反数,第二项利 ( http: / / www.21cnjy.com )用特殊角的三角函数值化简,第三项先计算绝对值里边的式子,再利用绝对值的代数意义化简,第四项利用零指数幂法则计算,即可得到结果.
解答: 解:原式=﹣4﹣+3+1+=0.
点评: 此题考查了实数的运算,涉及的知识有:零指数、负指数幂,平方根的定义,绝对值的代数意义,熟练掌握运算法则是解本题的关键.
28.(2013 安徽)计算:2sin30°+(﹣1)2﹣|2﹣|.
考点: 实数的运算;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 原式第一项利用特殊角的三角函数值化简,第二项表示两个﹣1的乘积,最后一项利用绝对值的代数意义化简,即可得到结果.
解答: 解:原式=2×+1﹣2+=.
点评: 此题考查了实数的运算,涉及的知识有:零指数、负指数幂,平方根的定义,绝对值的代数意义,熟练掌握运算法则是解本题的关键.
一、选择题(共10小题)
1.(2011 黔南州)有一个数值转换器,原理如下:当输入的x=64时,输出的y等于( )
( http: / / www.21cnjy.com )
A. 2 B. 8 C. D.
2.(2010 淮安)下面四个数中与最接近的数是( )
A. 2 B. 3 C. 4 D. 5
3.(2010 天津)比较2,,的大小,正确的是( )
A. B. C. D.
4.(2009 邵阳)与最接近的整数是( )
A. 0 B. 2 C. 4 D. 5
5.(2010 怀化)若0<x<1,则x,x2,x3的大小关系是( )
A. x<x2<x3 B. x<x3<x2 C. x3<x2<x D. x2<x3<x
6.(2010 金华)如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A. a<1<﹣a B. a<﹣a<1 C. 1<﹣a<a D. ﹣a<a<1
7.(2008 盐城)实数a在数轴上对应的点如图所示,则a,﹣a,1的大小关系正确的是( )
A. ﹣a<a<1 B. a<﹣a<1 C. 1<﹣a<a D. a<1<﹣a
8.(2008 北京)若|x+2|+,则xy的值为( )
A. ﹣8 B. ﹣6 C. 5 D. 6
9.(2013 永州)我们知道,一元二次 ( http: / / www.21cnjy.com )方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n i=(i4)n i=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为( )
A. 0 B. 1 C. ﹣1 D. i
10.(2012 湘潭)文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,若输入,则输出的结果为( )
A. 5 B. 6 C. 7 D. 8
二、填空题(共8小题)(除非特别说明,请填准确值)
11.(2013 湘潭)计算:= _________ .
12.(2012 东莞)若x,y为实数,且满足|x﹣3|+=0,则的值是 _________ .
13.(2013 台州)任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[]=1.现对72进行如下操作:72[]=8[]=2[]=1,这样对72只需进行3次操作后变为1,类似的,①对81只需进行 _________ 此操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 _________ .
14.(2012 汕头)若x,y为实数,且满足|x﹣3|+=0,则()2012的值是 _________ .
15.(2012 张家界)已知,则x+y= _________ .
16.(2012 常德)规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3.按此规定[]的值为 _________ .
17.(2012 南平)设[x)表示大于x的最小整数,如[3)=4,[﹣1.2)=﹣1,
则下列结论中正确的是 _________ .(填写所有正确结论的序号)
①[0)=0;②[x)﹣x的最小值是0;③[x)﹣x的最大值是0;④存在实数x,使[x)﹣x=0.5成立.
18.(2011 内江)已知|6﹣3m|+(n﹣5)2=3m﹣6﹣,则m﹣n= _________
三、解答题(共10小题)(选答题,不自动判卷)
19.(2013 常德)计算;(π﹣2)0++(﹣1)2013﹣()﹣2.
20.(2013 南宁)计算:20130﹣+2cos60°+(﹣2)
21.(2012 眉山)计算:4cos30°+()﹣2﹣(﹣1)
22.(2013 长沙)计算:.
23.(2013 重庆)计算:(﹣3)0﹣﹣(﹣1)2013﹣|﹣2|+(﹣)﹣2.
24.(2013 重庆)计算:.
25.(2012 崇左)如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣,设点B所表示的数为m.
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值.
26.(2012 遂宁)计算:﹣2sin45°+(2﹣π)0﹣.
27.(2013 凉山州)计算:.
28.(2013 安徽)计算:2sin30°+(﹣1)2﹣|2﹣|.
第3章 实数(教师讲评卷)
一、选择题(共10小题)
1.(2011 黔南州)有一个数值转换器,原理如下:当输入的x=64时,输出的y等于( )
( http: / / www.21cnjy.com )
A. 2 B. 8 C. D.
考点: 算术平方根.
专题: 压轴题;图表型.
分析: 根据图中的步骤,把64输入,可得其算术平方根为8,8再输入得其算术平方根是,是无理数则输出.
解答: 解:由图表得,64的算术平方根是8,8的算术平方根是;故选D.
点评: 本题考查了算术平方根的定义,看懂图表的原理是正确解答的关键.
2.(2010 淮安)下面四个数中与最接近的数是( )
A. 2 B. 3 C. 4 D. 5
考点: 估算无理数的大小.
分析: 先根据的平方是11,距离11最近的完全平方数是9和16,通过比较可知11距离9比较近,由此即可求解.
解答: 解:∵32=9,3.52=12.25,42=16∴<<<,∴与最接近的数是3,而非4.故选B.
点评: 此题主要考查了无理数的估算能力,通过比较二次根式的平方的大小来比较二次根式的大小是常用的一种比较方法和估算方法.
3.(2010 天津)比较2,,的大小,正确的是( )
A. B. C. D.
考点: 实数大小比较.
专题: 应用题.
分析: 首先把各数同时立方,然后比较被开方数的大小,即可解决问题.
解答: 解:∵23=8,()3=5≈11.2,()3=7∴<2<.故选C.
点评: 此题主要考查了实数大小的比较,本题可通过比较它们的立方来比较大小.
4.(2009 邵阳)与最接近的整数是( )
A. 0 B. 2 C. 4 D. 5
考点: 估算无理数的大小.
专题: 压轴题.
分析: 先估计的近似值,然后判断与最接近的整数即可求解.
解答: 解:∵1<3<4,∴1<<2.故选B
点评: 此题主要考查了正确根据平方进行估算的能力,现实生活中经常需要估算,估算应是我们具备的数学能力,“夹逼法”是估算的一般方法,也是常用方法.
5.(2010 怀化)若0<x<1,则x,x2,x3的大小关系是( )
A. x<x2<x3 B. x<x3<x2 C. x3<x2<x D. x2<x3<x
考点: 实数大小比较.
专题: 压轴题.
分析: 首先根据条件给出符合条件的具体数值,然后根据负数小于一切正数,两个负数比较大小,两个负数绝对值大的反而小即可解答.
解答: 解:∵0<x<1,∴假设x=,则x=,x2=,x3=,∵<<,∴x3<x2<x.故选C.
点评: 此题主要考查了实数的大小的比较,解答此题的关键是根据条件设出符合条件的具体数值,再即可方便比较大小.
6.(2010 金华)如图,若A是实数a在数轴上对应的点,则关于a,﹣a,1的大小关系表示正确的是( )
A. a<1<﹣a B. a<﹣a<1 C. 1<﹣a<a D. ﹣a<a<1
考点: 实数与数轴.
分析: 根据数轴可以得到a<1<﹣a,据此即可确定哪个选项正确.
解答: 解:∵实数a在数轴上原点的左边,∴a<0,但|a|>1,﹣a>1,则有a<1<﹣a.故选A.
点评: 本题考查了实数与数轴的对应关系,数轴上的数右边的数总是大于左边的数
7.(2008 盐城)实数a在数轴上对应的点如图所示,则a,﹣a,1的大小关系正确的是( )
A. ﹣a<a<1 B. a<﹣a<1 C. 1<﹣a<a D. a<1<﹣a
考点: 实数与数轴;实数大小比较.
专题: 压轴题.
分析: 本题首先运用数形结合的思想确定a的正负情况,然后根据相反数意义即可解题.
解答: 解:由数轴上a的位置可知a<0,|a|>1;设a=﹣2,则﹣a=2,∵﹣2<1<2∴a<1<﹣a,故选项A,B,C错误,选项D正确.故选D.
点评: 此题主要考查了比较实数的大小,解答此题的关键是根据数轴上a的位置估算出a的值,设出符合条件的数值,再比较大小即可.
8.(2008 北京)若|x+2|+,则xy的值为( )
A. ﹣8 B. ﹣6 C. 5 D. 6
考点: 非负数的性质:算术平方根;非负数的性质:绝对值.
专题: 压轴题.
分析: 已知任何数的绝对值一定是非负数,二次根式的 ( http: / / www.21cnjy.com )值一定是一个非负数,由于已知的两个非负数的和是0,根据非负数的性质得到这两个非负数一定都是0,从而得到一个关于x、y的方程组,解方程组就可以得到x、y的值,进而求出xy的值.
解答: 解:∵|x+2|≥0,≥0,而|x+2|+=0,∴x+2=0且y﹣3=0,∴x=﹣2,y=3,∴xy=(﹣2)×3=﹣6.故选:B.
点评: 本题考查的是非负数的性质,一元一次方程的解法及代数式的求值.题目注重基础,比较简单.
9.(2013 永州)我们知道,一元二次方 ( http: / / www.21cnjy.com )程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n i=(i4)n i=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013的值为( )
A. 0 B. 1 C. ﹣1 D. i
考点: 实数的运算.
专题: 压轴题;新定义.
分析: i1=i,i2=﹣1,i3 ( http: / / www.21cnjy.com )=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,i5=i4 i=i,i6=i5 i=﹣1,从而可得4次一循环,一个循环内的和为0,计算即可.
解答: 解:由题意得,i1=i,i2=﹣1,i ( http: / / www.21cnjy.com )3=i2 i=(﹣1) i=﹣i,i4=(i2)2=(﹣1)2=1,i5=i4 i=i,i6=i5 i=﹣1,故可发现4次一循环,一个循环内的和为0,∵=503…1,∴i+i2+i3+i4+…+i2012+i2013=i.故选D.
点评: 本题考查了实数的运算,解答本题的关键是计算出前面几个数的值,发现规律,求出一个循环内的和再计算,有一定难度.
10.(2012 湘潭)文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,若输入,则输出的结果为( )
A. 5 B. 6 C. 7 D. 8
考点: 实数的运算.
专题: 压轴题.
分析: 根据运算程序得出输出数的式子,再根据实数的运算计算出此数即可.
解答: 解:∵输入一个数后,输出的数比输入的数的平方小1,∴输入,则输出的结果为()2﹣1=7﹣1=6.故选B.
点评: 本题考查的是实数的运算,根据题意得出输出数的式子是解答此题的关键.
二、填空题(共8小题)(除非特别说明,请填准确值)
11.(2013 湘潭)计算:= 2 .
考点: 实数的运算;零指数幂;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 本题涉及零指数幂、特殊角的三角函数值、二次根式化简等考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式=×+1=1+1=2.故答案为2.
点评: 本题考查实数的综合运算能力,是各地 ( http: / / www.21cnjy.com )中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握零指数幂、特殊角的三角函数值、二次根式化简等考点的运算.
12.(2012 东莞)若x,y为实数,且满足|x﹣3|+=0,则的值是 1 .
考点: 非负数的性质:算术平方根;非负数的性质:绝对值.
专题: 压轴题.
分析: 根据非负数的性质列式求出x、y的值,再代入代数式进行计算即可得解.
解答: 解:根据题意得,x﹣3=0,y+3=0,解得x=3,y=﹣3,所以,()2012=()2012=1.故答案为:1.
点评: 本题考查了绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.
13.(2013 台州)任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[]=1.现对72进行如下操作:72[]=8[]=2[]=1,这样对72只需进行3次操作后变为1,类似的,①对81只需进行 3 此操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 255 .
考点: 估算无理数的大小.
专题: 压轴题;新定义.
分析: ①根据规律依次求出即可;②要想确 ( http: / / www.21cnjy.com )定只需进行3次操作后变为1的所有正整数,关键是确定二次操作后数的大小不能大于4,二次操作时根号内的数必须小于16,而一次操作时正整数255却好满足这一条件,即最大的正整数为255.
解答: 解:①[]=9,[]=3,[]=1,故答案为:3;②最大的是255,[]=15,[]=3,[]=1,而[]=16,[]=4,[]=2,[]=1,即只需进行3次操作后变为1的所有正整数中,最大的正整数是255,故答案为:255.
点评: 本题考查了估算无理数的大小的应用,主要考查学生的阅读能力和猜想能力.
14.(2012 汕头)若x,y为实数,且满足|x﹣3|+=0,则()2012的值是 1 .
考点: 非负数的性质:算术平方根;非负数的性质:绝对值.
分析: 根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可
解答: 解:根据题意得:,解得:.则()2012=()2012=1.故答案是:1.
点评: 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.
15.(2012 张家界)已知,则x+y= 1 .
考点: 非负数的性质:算术平方根;非负数的性质:偶次方.
专题: 计算题;压轴题.
分析: 根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.
解答: 解:∵,∴,解得,则x+y=﹣1+2=1,故答案为1.
点评: 本题考查了非负数的性质,利用该性质建立关于x、y的方程组是解题的关键.
16.(2012 常德)规定用符号[m]表示一个实数m的整数部分,例如:[]=0,[3.14]=3.按此规定[]的值为 4 .
考点: 估算无理数的大小.
专题: 压轴题;新定义.
分析: 求出的范围,求出+1的范围,即可求出答案.
解答: 解:∵3<<4,∴3+1<+1<4+1,∴4<+1<5,∴[+1]=4,故答案为:4.
点评: 本题考查了估计无理数的应用,关键是确定+1的范围,题目比较新颖,是一道比较好的题目.
17.(2012 南平)设[x)表示大于x的最小整数,如[3)=4,[﹣1.2)=﹣1,
则下列结论中正确的是 ④ .(填写所有正确结论的序号)
①[0)=0;②[x)﹣x的最小值是0;③[x)﹣x的最大值是0;④存在实数x,使[x)﹣x=0.5成立.
考点: 实数的运算.
专题: 压轴题;新定义.
分析: 根据题意[x)表示大于x的最小整数,结合各项进行判断即可得出答案.
解答: 解:①[0)=1,故本项错误;②[x)﹣x>0,但是取不到0,故本项错误;③[x)﹣x≤1,即最大值为1,故本项错误;④存在实数x,使[x)﹣x=0.5成立,例如x=0.5时,故本项正确.故答案为④.
点评: 此题考查了实数的运算,仔细审题,理解[x)表示大于x的最小整数是解答本题的关键,难度一般.
18.(2011 内江)已知|6﹣3m|+(n﹣5)2=3m﹣6﹣,则m﹣n= ﹣2
考点: 非负数的性质:算术平方根;非负数的性质:绝对值;非负数的性质:偶次方.
分析: 根据|6﹣3m|+(n﹣5)2=3m﹣6﹣,得出6﹣3m≤0,将已知等式化简,可得n﹣5=0,以及m﹣3=0,即可求出n,m的值,即可得出答案.
解答: 解:∵|6﹣3m|+(n﹣5)2=3m﹣6﹣,∴6﹣3m≤0,m﹣3≥0,∴m≥3,∴已知等式化简,得(n﹣5)2=﹣,∴(n﹣5)2+=0,∴n﹣5=0,n=5,∴m﹣3=0,m=3,则m﹣n=3﹣5=﹣2.故答案为:﹣2.
点评: 此题主要考查了算术平方根以及绝对值的性质,根据题意得出n,m的值是解决问题的关键.
三、解答题(共10小题)(选答题,不自动判卷)
19.(2013 常德)
考点: 实数的运算;零指数幂;负整数指数幂.
专题: 压轴题.
分析: 分别进行零指数幂、负整数指数幂及二次根式的化简,然后合并可得出答案.
解答: 解:
点评: 本题考查了实数的运算,涉及了零指数幂、负整数指数幂的运算,解答本题的关键是掌握各部分的运算法则.
20.(2013 南宁)计算:20130﹣+2cos60°+(﹣2)
考点: 实数的运算;零指数幂;特殊角的三角函数值.
专题: 压轴题.
分析: 分别进行零指数幂、二次根式的化简,然后代入特殊角的三角函数值合并即可得出答案.
解答: 解:原式=1﹣3+2×﹣2=﹣3.
点评: 本题考查了实数的运算,属于基础题,关键是掌握零指数幂的运算法则及一些特殊角的三角函数值.
21.(2012 眉山)计算:4cos30°+()﹣2﹣(﹣1)
考点: 实数的运算;负整数指数幂;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 根据负整数指数幂的意义和cos30°=得到原式=4×+4﹣2+1,再进行乘法运算,然后合并即可.
解答: 解:原式=4×+4﹣2+1=2+4﹣2+1=5.
点评: 本题考查了实数的运算:先进行乘法运算,再进行乘除运算,然后进行加减运算;有括号先算括号.也考查了负整数指数幂与特殊角的三角函数值.
22.(2013 长沙)计算:.
考点: 实数的运算;零指数幂.
专题: 压轴题.
分析: 分别进行绝对值、平方及零指数幂的运算,然后合并即可得出答案.
解答: 解:原式=3+4﹣1=6.
点评: 本题考查了实数的运算,属于基础题,掌握各部分的运算法则 是关键.
23.(2013 重庆)计算:(﹣3)0﹣﹣(﹣1)2013﹣|﹣2|+(﹣)﹣2.
考点: 实数的运算;零指数幂;负整数指数幂.
专题: 计算题;压轴题.
分析: 原式第一项利用零指数幂法则计算,第二项利用平 ( http: / / www.21cnjy.com )方根的定义化简,第三项表示2013个﹣1的乘积,第四项利用负数的绝对值等于它的相反数计算,最后一项利用负指数幂法则计算即可得到结果.
解答: 解:原式=1﹣3+1﹣2+9=6.
点评: 此题考查了实数的运算,涉及的知识有:零指数、负指数幂,平方根的定义,绝对值的代数意义,熟练掌握运算法则是解本题的关键.
24.(2013 重庆)计算:.
考点: 实数的运算;零指数幂;负整数指数幂.
专题: 压轴题.
分析: 分别进行乘方、绝对值、零指数幂、开立方等运算,然后按照实数的运算法则计算即可.
解答: 解:原式=﹣1﹣2+1×2+4=3.
点评: 本题考查了实数的运算,涉及了乘方、绝对值、零指数幂、开立方等知识,属于基础题.
25.(2012 崇左)如图,一只蚂蚁从点A沿数轴向右直爬2个单位到达点B,点A表示﹣,设点B所表示的数为m.
(1)求m的值;
(2)求|m﹣1|+(m+6)0的值.
考点: 实数与数轴;零指数幂.
专题: 图表型.
分析: (1)根据正负数的意义计算;(2)根据绝对值的意义和零指数幂的运算法则计算.
解答: 解:(1)由题意A点和B点的距离为2,其A点的坐标为﹣,因此B点坐标m=2﹣.(2)把m的值代入得:|m﹣1|+(m+6)0=|2﹣﹣1|+(2﹣+6)0,=|1﹣|+(8﹣)0,=﹣1+1,=.
点评: 本题考查了含有零指数幂的运算,任何非0数的0次幂等于1,还要注意去绝对值符号时,结果为非负数.
26.(2012 遂宁)计算:﹣2sin45°+(2﹣π)0﹣.
考点: 实数的运算;零指数幂;负整数指数幂;二次根式的性质与化简;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 本题涉及零指数幂、负整数指 ( http: / / www.21cnjy.com )数幂、特殊角的三角函数值、二次根式化简四个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答: 解:原式==.
点评: 本题考查实数的运算能力, ( http: / / www.21cnjy.com )解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式等考点的运算.注意:负指数为正指数的倒数;任何非0数的0次幂等于1;二次根式的化简是根号下不能含有分母和能开方的数.
27.(2013 凉山州)计算:.
考点: 实数的运算;零指数幂;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 原式第一项表示2平方的相反数,第二项利 ( http: / / www.21cnjy.com )用特殊角的三角函数值化简,第三项先计算绝对值里边的式子,再利用绝对值的代数意义化简,第四项利用零指数幂法则计算,即可得到结果.
解答: 解:原式=﹣4﹣+3+1+=0.
点评: 此题考查了实数的运算,涉及的知识有:零指数、负指数幂,平方根的定义,绝对值的代数意义,熟练掌握运算法则是解本题的关键.
28.(2013 安徽)计算:2sin30°+(﹣1)2﹣|2﹣|.
考点: 实数的运算;特殊角的三角函数值.
专题: 计算题;压轴题.
分析: 原式第一项利用特殊角的三角函数值化简,第二项表示两个﹣1的乘积,最后一项利用绝对值的代数意义化简,即可得到结果.
解答: 解:原式=2×+1﹣2+=.
点评: 此题考查了实数的运算,涉及的知识有:零指数、负指数幂,平方根的定义,绝对值的代数意义,熟练掌握运算法则是解本题的关键.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
