6.3反比例函数的应用 同步讲义(含解析)八年级数学下册浙教版
文档属性
| 名称 | 6.3反比例函数的应用 同步讲义(含解析)八年级数学下册浙教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 00:00:00 | ||
图片预览




文档简介
专题6.3 反比例函数的应用
1.掌握用反比例函数解决实际问题
2.掌握反比例函数在其他学科中的应用
知识点 实际问题与反比例函数
【知识点】
知识点一、利用反比例函数解决实际问题
1.基本思路:建立函数模型,即在实际问题中求得函数解析式,然后应用函数的图象和性质等知识解决问题.
2.一般步骤如下:
(1)审清题意,根据常量、变量之间的关系,设出函数解析式,待定的系数用字母表示。(2)由题目中的已知条件,列出方程,求出待定系数.
(3)写出函数解析式,并注意解析式中变量的取值范围.
(4)利用函数解析式、函数的图象和性质等去解决问题.
知识点二、反比例函数在其他学科中的应用
1.当圆柱体的体积一定时,圆柱的底面积是高的反比例函数;
2.当工程总量一定时,做工时间是做工速度的反比例函数;
3.在使用杠杆时,如果阻力和阻力臂不变,则动力是动力臂的反比例函数;
【典型例题】
1.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压(单位:)是气体体积(单位:)的反比例函数:,能够反映两个变量和函数关系的图象是( )
A. B.
C. D.
2.小明设计了杠杆平衡实验:如图,取一根长质地均匀的木杆,用细绳绑在木杆的中点O处并将其吊起来,在左侧距离中点O处挂一个重的物体,在中点O右侧用一个弹簧测力计竖直向下拉,以保持木杆水平(动力×动力臂=阻力×阻力臂).改变弹簧测力计与中点O的距离L(单位:),观察并记录弹簧测力计的示数F(单位:N)有什么变化.小明根据实验得到的下列结论中,不正确的是( )
A.L与F的函数关系式为 B.当时,
C.当时, D.保持木杆水平,F的最小值为10
3.在一个可以改变体积的密闭容器内装有一定质量的气体,当改变容器的体积时,气体的密度也会随之改变,密度是体积的反比例函数,它的图象如图所示,根据图象可知,下列说法正确的是( )
A.密度随体积的增大而增大
B.密度和体积的关系式为
C.密度时,体积的范围为
D.体积时,密度的范围为
4.近视眼镜是一种为了矫正视力,让人们可以清晰看到远距离物体的凹透镜片.研究发现,近视眼镜的度数y(度)与镜片焦距的函数关系如图所示,则下列说法中错误的是( )
A.当x的值增大时,y的值随之减小
B.当焦距x为时,近视眼镜的度数y为500度
C.当焦距x为时,近视眼镜的度数y约300度
D.某人近视度数400度,镜片焦距应该调试为
5.如表记录了一组物理试验数据,已知当温度不变时,气球内气体的压强(单位:)是气体体积(单位:)的函数,则与的函数关系式是 .
(单位:)
(单位:)
6.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积V是反比例函数关系,它的图象如图所示,当时,.
若,二氧化碳密度的变化范围
7.研究发现,近视眼镜的度数y(度)与镜片焦距x(米)成反比例函数关系,李阳佩戴的度近视镜片的焦距为米,经过一段时间的矫正治疗加之注意用眼健康,验光测得现在镜片焦距为米,则李阳的近视眼镜度数可以调整为 度.
8.为预防传染病,某校定期对教室进行“药熏消毒”.如图所示,药物燃烧阶段,教室内每立方米空气中的含药量与燃烧时间(分)成正比例;燃烧后,与成反比例.若,则的取值范围是 .
9.古希腊科学家阿基米德曾说“给我一个支点,我可以撬动地球”.后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力阻力臂动力动力臂(如图).小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别为和.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为2米时,撬动石头至少需要多大的力?
(2)若想使动力F不超过(1)中所用力的一半,则动力臂l至少要加长多少?
10.如图,取一根长米的质地均匀木杆,用细绳绑在木杆的中点处并将其吊起来,在中点的左侧距离中点处挂一个重牛的物体,在中点右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧称与中点的距离(单位:),看弹簧秤的示数(单位:牛,精确到牛)有什么变化,小慧在做此《数学活动》时,得到下表的数据:
牛
结果老师发现其中有一个数据明显有错误.
(1)你认为当______时所对应的数据是明显错误的;
(2)在已学过的函数中选择合适的模型求出与的函数关系式;
(3)若弹簧秤的最大量程是牛,求的取值范围.
【即学即练】
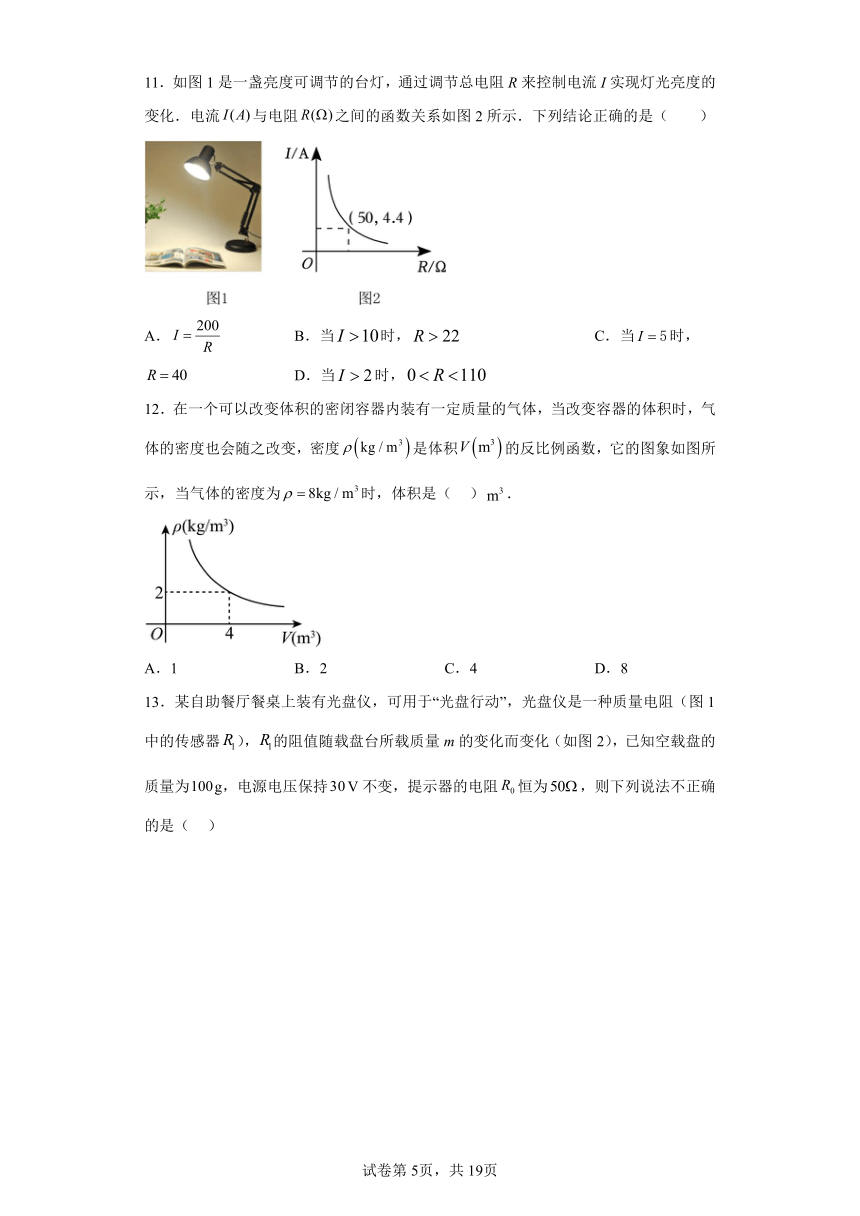
11.如图1是一盏亮度可调节的台灯,通过调节总电阻R来控制电流I实现灯光亮度的变化.电流与电阻之间的函数关系如图2所示.下列结论正确的是( )
A. B.当时, C.当时, D.当时,
12.在一个可以改变体积的密闭容器内装有一定质量的气体,当改变容器的体积时,气体的密度也会随之改变,密度是体积的反比例函数,它的图象如图所示,当气体的密度为时,体积是( ).
A.1 B.2 C.4 D.8
13.某自助餐厅餐桌上装有光盘仪,可用于“光盘行动”,光盘仪是一种质量电阻(图1中的传感器),的阻值随载盘台所载质量m的变化而变化(如图2),已知空载盘的质量为g,电源电压保持V不变,提示器的电阻恒为,则下列说法不正确的是( )
A.载盘台所载质量m越大,传感器的阻值越小
B.当g时,的阻值为
C.当g时,提示器不会发出提示音
D.当时,提示器会发出提示音
14.一定电压(单位:V)下电流和电阻之间成反比例关系,东东用一个蓄电池作为电源组装了一个电路如图1所示,通过实验,发现电流随着电阻值的变化而变化的一组数据如表格所示.
R(Ω) … 2 3 4 6 12 …
I(A) … 24 16 12 a 4 …
下列说法不正确的是( )
A.表中
B.这个蓄电池的电压值是48V
C.图2中图象可以表示电流I和电阻R之间的函数关系
D.若该电路的最小电阻值为1.5Ω,该电路能通过的最大电流是34A
15.物理学中,在压力F不变的情况下,某物体承受的压强P与它的受力面积S成反比例函数关系,则下表中压强与的大小关系为: .(填“”,“”或“”)
16.由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值R(始终保持),发现通过滑动变阻器的电流I与滑动变阻器的电阻R成反比例函数关系,它的图象如图所示,若使得通过滑动变阻器的电流不超过,则滑动变阻器阻值的范围是 .
17.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为元/双,要使该款运动鞋每天的销售利润达到元,则其售价应定为 元.
售价x(元/双) 200 250 300 400
销售量y(双) 30 24 20 15
18.为预防“新冠病毒”,学校对教室喷洒消毒液(含氯消毒剂)进行消杀,资料表明空气中氯含量不低于,才能有效杀灭新冠病毒.如图,喷洒消毒液时教室空气中的氯含量与时间成正比例,消毒液挥发时,与成反比例,则此次消杀的有效作用时间是 min.
19.如图所示是某一蓄水池每小时的排水量与排完水池中的水所用的时间之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)求出此函数的解析式;
(3)若要排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时排水量不超过,那么水池中的水至少要多少小时排完?
20.某水果生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度与时间之间的函数关系,其中线段表示恒温系统开启后阶段,双曲线的一部分表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)这个恒温系统设定的恒定温度为多少;
(2)求全天的温度与时间之间的函数关系式;
(3)若大棚内的温度低于不利于新品种水果的生长,问这天内,相对有利于水果生长的时间共多少小时?
题组A 基础过关练
(2023·辽宁大连·统考一模)
21.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力阻力臂动力动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1000N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A. B. C. D.
(2023春·江苏·八年级专题练习)
22.已知圆柱的侧面积是,若圆柱底面半径为,高为,则关于的函数图象大致是( )
A. B. C. D.
(2023秋·河北张家口·九年级校考阶段练习)
23.一定电压下通过导体的电流I(A)和电阻R(Ω)之间成反比例函数,小明通过组合电路做实验时,发现电流I(A)随着电阻R(Ω)的变化而变化,其数据如下表所示.若在该电路中,电流表的最大量程是3A,为确保不超过电流表的最大量程,则该电路中电阻不小于( )
R(Ω) … 2 3 4 …
I(A) … 2.4 1.6 1.2 …
A.2Ω B.1.8Ω C.1.6Ω D.1.5Ω
(2022春·全国·九年级专题练习)
24.学校的自动饮水机,通电加热时水温每分钟上升,加热到时,自动停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则水温要从加热到,所需要的时间为( )
A. B. C. D.
(2023春·江苏苏州·八年级统考期中)
25.矩形的面积为2,两条邻边长分别为x,y,则y关于x的函数关系式为 .
(2022春·全国·九年级专题练习)
26.一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力、、、,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是 同学.
(2022秋·福建福州·九年级福建省福州第八中学校考阶段练习)
27.密闭容器内有一定质量的二氧化碳,在温度不变的情况下,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ是体积V的反比例函数关系,它的图象如图所示,则当ρ = 3.3 kg/m3时,相应的体积V是 m3.
(2023·山西吕梁·校考模拟预测)
28.某物体对地面的压强P(Pa)与物体和地面的接触面积S(m2)成反比例函数关系(如图),当该物体与地面的接触面积为0.25m2时,该物体对地面的压强是 Pa.
(2023·浙江丽水·统考一模)
29.如图,取一根长的均匀木杆,用细绳绑在木杆的中点并将其吊起来.在中点的左侧挂一个物体,在中点的右侧用一个弹簧秤向下拉,使木杆处于水平状态.根据杠杆原理,当物体保持不动时,弹簧秤的示数(单位:)是(弹簧秤与中点的距离)(单位:)的反比例函数,当时,.
(1)求关于的函数表达式.
(2)移动弹簧秤的位置,若木杆仍处于水平状态,求弹簧秤的示数的最小值.
(2022春·全国·九年级专题练习)
30.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)这个反比例函数的解析式是 ().
(2)若使用时电阻,则电流I是
(3)如果以蓄电池为电源的用电器的电流不能超过10A,那么用电器的可变电阻至少是多少?
题组B 能力提升练
(2023春·八年级课时练习)
31.港珠澳大桥桥隧全长55千米,其中主桥长29.6千米,一辆汽车从主桥通过时,汽车的平均速度 v(千米/时)与时间 t(小时)的函数关系式为( )
A. B. C.v=29.6t D.
(2023·福建福州·统考一模)
32.公元前3世纪,古希腊科学家阿基米德发现了“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂,当用撬棍撬动一块石头时,发现阻力和阻力臂分别为和,关于动力F和动力臂l,下列说法错误的是( )
A.F与l的积为定值
B.F随l的增大而减小
C.当l为时,撬动石头至少需要的力
D.F关于l的函数图象位于第一、第三象限
(2023秋·山东威海·九年级统考期末)
33.某蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,其图象如图所示.若以此蓄电池为电源的用电器,其限制电流不超过,那么用电器可变电阻应控制的范围是( )
A. B. C. D.
(2023秋·河南开封·九年级统考期末)
34.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:)与电阻R(单位:)是反比例函数关系,它的图象如图所示,下列说法正确的个数是( )
①这个反比例函数解析式为;②蓄电池的电压是;③当时,;④当时,
A.4 B.3 C.2 D.1
(2023·山西长治·校联考二模)
35.某数学小组在“探究杠杆平衡条件”实验中固定阻力和阻力臂,得到了下表中的动力与动力臂的几组对应值,根据学习经验,下表中a的值为 .
… 1.5 2 3 4 5 6 …
… 8 6 4 3 a 2 …
(2023·山东菏泽·统考一模)
36.公元前3世纪,古希结科学家阿基米德发现了“杠杆原理”,杠杆平衡时,阻力×阻力臂动力×动力臂,当用撬棍撬动一块石头时,发现阻力和阻力臂分别为1200N和m,关于动力F和动力臂l:①F与l的积为定值;②F随l的增大而减小;③当l为1.5m时,撬动石头至少需要400N的力;④F关于l的函数图象位于第一、第三象限,上面四种说法错误的是 .
(2023秋·河南信阳·九年级统考期末)
37.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系,其图象为如图所示的一段曲线,且端点为和.若行驶速度不得超过60km/h,则汽车通过该路段最少需要 h?
(2023春·江苏·八年级专题练习)
38.青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差 小时.
(2023春·山西晋城·八年级统考期中)
39.如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:)是物距(小孔到蜡烛的距离)x(单位:)的反比例函数,当时,
(1)求y关于x的函数表达式;
(2)若火焰的像高为,求小孔到蜡烛的距离.
(2023·河南焦作·统考一模)
40.如图,某种品牌的电动车的蓄电池电压为定值,使用电源时,电流是电阻的反比例函数,其图象经过,两点.
(1)求I与R的函数表达式,并说明比例系数的实际意义;
(2)求m的值,并说明m的实际意义;
(3)如果以蓄电池为电源的用电器限制电流不得超过,那么用电器的可变电阻应控制在什么范围内?
题组C 培优拔尖练
(2023·江苏常州·统考二模)
41.一村民在清理鱼塘时不慎被困淤泥中,消防队员以门板作船进行救援,设人和门板对淤泥的压力合计,门板面积为,则人和门板对淤泥的压强和门板面积之间的函数关系式为( )
A. B. C. D.
(2023·河南周口·统考一模)
42.很多学生由于学习时间过长,用眼不科学,视力下降,国家“双减”政策的目标之一就是减轻学生的作业辅导,让学生提质增效,近视眼镜可以清晰看到远距离物体,它的镜片是凹透镜,研究发现,近视眼镜的度数y(度)与镜片焦距x(m)的关系式为.下列说法不正确的是( )
A.上述问题中,当x的值增大,y的值随之减小
B.当镜片焦距是0.2m时,近视眼镜的度数是500度
C.当近视眼镜的度数是400度时,镜片焦距是0.25m
D.东东原来佩量400度的近视眼镜,经过一段时间的矫正治疗加注意用眼健康,复查验光时,所配镜片焦距调整为0.4m,则东东的眼镜度数下降了200度
(2023·河南濮阳·统考一模)
43.如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点O的距离,观察弹簧测力计的示数的变化情况.实验数据记录如下表:
…… 10 15 20 25 30 ……
…… 45 30 22.5 18 15 ……
下列说法不正确的是( )
A.弹簧测力计的示数与支点O的距离之间关系的图像如图
B.y与x的函数关系式为
C.当弹簧测力计的示数为时,弹簧测力计与O点的距离是37.5
D.随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小
(2023·河南驻马店·校考二模)
44.一款简易电子秤的工作原理:一个装有踏板(踏板质量忽略不计)的可变电阻,与踏板人的质量m之间的函数关系式为,其图象如图1所示;图2的电路中,电源电压恒为12伏,定值电阻的阻值为60欧,接通开关,人站上踏板,电流表显示的读数为I安,该读数可以换算为人的质量m,电流表量程为0~0.2安(温馨提示:导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式),则下面结论错误的为( )
A.用含I的代数式表示为
B.电子体重秤可称的最大质量为120千克
C.当时,若电源电压U为12(伏),则定值电阻最小为70(欧)
D.当时,若定值电阻为40(欧),则电源电压U最大为10(伏)
(2023·山东临沂·统考一模)
45.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的学校是 .
(2023春·八年级课时练习)
46.为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物熏蒸消毒.消毒药物在一间教室内空气中的浓度y(单位:)与时间x(单位:)的函数关系如图所示:校医进行药物熏蒸时y与x的函数关系式为,药物熏蒸完成后y与x成反比例函数关系,两个函数图象的交点为.教室空气中的药物浓度不低于于时,对杀灭病毒有效.当时,本次消毒过程中有效杀灭病毒的时间为 min
(2023秋·河北保定·九年级统考期末)
47.如图是6个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角和凹入的角的顶点记作(n为1~11的整数),函数的图象为L.
(1)若L过点,则 ;
(2)若L过,则L一定过另一点,则 ;
(3)若L使得这些点分布在它的两侧,且一侧5个点一侧6个点,请写出符合要求的k的所有整数值: .
(2023·山东济南·一模)
48.饮水机中原有水的温度为,通电开机后,饮水机自动开始加热(此过程中,水温与开机时间分满足一次函数关系),当加热到时自动停止加热,随后水温开始下降(此过程中,水温与开机时间x分成反比例函数关系),当水温降至时,饮水机又自动开始加热,……如此循环下去(如图所示).那么开机后分钟时,水的温度是 .
(2022秋·九年级单元测试)
49.某商场出售一批进价为2元的贺卡,在市场营销中发现,此种贺卡的销售单价x(单位:元)与日销售量y(单位:张)之间有如下关系:
销售单价x(元) 3 4 5 6
日销售量y(张) 20 15 12 10
(1)根据表中数据在平面直角坐标系中描出实数对的对应点;
(2)确定y与x之间的函数关系式,并画出图象;
(3)设此种贺卡的日销售利润为w元,试求出w与x之间的函数关系式.若物价局规定此种贺卡的售价最高不超过10元/张,请你求出销售单价x定为多少元时,才能获得最大日销售利润?并求出最大日销售利润.
(2023春·河南南阳·八年级统考期中)
50.为了探索函数 的图象与性质,我们参照学习函数的过程与方法.
x … 1 1.5 2 3 4.5 6 9 …
y … 10 7.5 6.5 6 6.5 7.5 10 …
列表:
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
(1)观察所描出点的分布,用一条光滑的曲线将点顺次连接起来,作出函数图象.
(2)已知点(x ,y )、(x ,y )在函数图象上,结合表格和函数图象,回答下列问题(填“>”“=”或“<”):
①若 , 则;
②若 , 则;
③若,则
(3)某农户要用一些围栏建造一个的长方形鸡圈,设鸡圈的一边长为,所需围栏长度为.
①请直接写出y与x之间的函数关系式;
②若围栏的单价为50元/m,且该农户买围栏的预算不超过750元,在不考虑其他影响因素的情况下,鸡圈的一边长x应控制在什么范围内
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.B
【分析】根据实际意义以及函数的解析式,根据函数的类型,以及自变量的取值范围即可进行判断.
【详解】解:当m一定时,与V之间成反比例函数,则函数图象是双曲线,同时自变量是正数.
故选:B.
【点睛】此题主要考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
2.C
【分析】根据动力×动力臂=阻力×阻力臂,可得出即即可得出结论.
【详解】解:∵动力×动力臂=阻力×阻力臂,
故选项正确,不符合题意.
∴当时,,
故选项正确,不符合题意.
∴当时,,
∴故选项错误,符合题意.
∵一根长质地均匀的木杆,用细绳绑在木杆的中点O处并将其吊起来,
∴右侧最长为,
故选项正确,不符合题意.
故选:
【点睛】本题主要考查了反比例函数与实际问题的综合,熟练掌握反比例函数的性质是解此题的关键.
3.C
【分析】求得反比例函数的关系式,根据反比例函数的性质解答即可.
【详解】解:观察图象,密度是体积的反比例函数,且经过点,
设反比例函数的关系式为,则,
∴函数关系式为,
A、密度随体积的增大而减少,原说法错误,本选项不符合题意;
B、密度和体积的关系式为,原说法错误,本选项不符合题意;
C、密度时,体积的范围为,正确,,本选项符合题意;
D、体积时,密度的范围为,原说法错误,本选项不符合题意;
故选:C.
【点睛】本题考查了反比例函数的应用,利用待定系数法求得比例函数的关系式是解题的关键.
4.D
【分析】根据反比例函数的性质可以判断A;利用已知解析式代入相关数据可以判断B,C,D.
【详解】∵近视眼镜的度数y(度)与镜片焦距的关系式为,
∴当x的值增大时,y的值随之减小,故A正确,不符合题意;
将代入,y值为500,故B正确,不符合题意;
将.代入,y值约为333,故C正确,不符合题意;
将代入,x值为0.25,故D错误,符合题意.
故选D.
【点睛】本题考查了反比例函数的应用,正确利用反比例函数的性质是解题关键.
5.
【分析】观察表格发现,从而确定两个变量之间的关系即可.
【详解】解:观察发现:,
故与的函数关系式为,
故答案为:.
【点睛】本题考查了反比例函数的应用,解题的关键是能够观察表格并发现两个变量的乘积为常数,难度不大.
6.
【分析】观察函数图像,根据函数图像上点的坐标,利用待定系数法可求出反比例函数的解析式,再利用反比例函数图像上点的坐标特征,即可求出答案.
【详解】解:∵密度与体积V是反比例函数关系,
∴设,
∵当时,,
∴,
∴,
∴密度关于体积V的函数解析式为:;
观察函数图象可知,随V的增大而减小,
当时,,
当时,,
∴当时,
即二氧化碳密度的变化范围是,
故答案为:.
【点睛】本题考查反比例函数的实际应用,掌握反比例函数图象的性质是解题的关键.
7.
【分析】设函数为,将度近视镜片的焦距为米代入求出k,再将米代入求解即可得到答案;
【详解】解:设函数为,将度近视镜片的焦距为米代入得,、
,解得:,
∴,
将代入求解可得,
,
故答案为:;
【点睛】本题考查待定系数法求解析式及函数值,解题的关键是根据题意找点代入.
8.
【分析】由函数图象得出相应函数关系式,再根据题目要求求出x的取值范围即可;
【详解】解:函数图象可知,
燃烧时,与成正比例函数: ,
将代入得,即,
∴,
燃烧后,与成反比例函数:,
将代入得,即,
∴,
∵,
∴即;即,
∴的取值范围是.
故答案为:.
【点睛】本题主要考查正比例函数、反比例函数的应用,正确理解题意并列出函数关系式是解题的关键.
9.(1)动力F与动力臂l的函数关系为,动力臂为2米时,撬动石头至少需要的力;
(2)动力臂至少要加长.
【分析】(1)直接利用:阻力阻力臂动力动力臂,进而得出F与l之间的关系;
(2)直接利用动力F不超过题(1)中所用力的一半,进而得出l的值.
【详解】(1)解:由题意可得:,
则,
当动力臂为2米时,
则撬动石头至少需要:,
答:动力F与动力臂l的函数关系为,动力臂为2米时,撬动石头至少需要的力;
(2)解:当动力F不超过题(1)中所用力的一半,即,
则,
解得:,
即动力臂至少要加长,
答:动力臂至少要加长.
【点睛】此题主要考查了反比例函数的应用,正确得出F与l之间的关系是解题关键.
10.(1);
(2);
(3).
【分析】(1)根据表格数据,可发现与的乘积为定值,从而可得答案;
(2)根据=,可得与的函数解析式;
(3)根据弹簧秤的最大量程是牛,即可得到结论.
【详解】(1)解:根据表格数据可知 ,
当时,牛,所以表格中数据错了,
故答案为:15;
(2)解:表格数据知.
F与L的函数关系式为:;
(3)解:当牛时,由,得,根据反比例函数的图象与性质可得,
由题意可知,L的取值范围是.
【点睛】本题考查了反比例函数的应用,解答本题的关键是仔细观察表格,得出F与L的积为定值,从而得出函数关系式.
11.D
【分析】由图象可知,电流与电阻之间满足反比例函数关系,设电流与电阻之间的函数关系为,根据点在函数的图象上得,进行计算得电流与电阻之间的函数关系为,当时,则,解得,由函数图象可知,该函数在第一象限内y随x的增大而减小,则当时,;当时,则,得;当时,则,计算得,由函数图象可知,该函数在第一象限内y随x的增大而减小,当时,;综上,即可得.
【详解】解:由图象可知,电流与电阻之间满足反比例函数关系,
设电流与电阻之间的函数关系为,
∵点在函数的图象上,
∴,
解得:,
∴电流与电阻之间的函数关系为,故A选项错误,不符合题意;
当时,则,
∴,
由函数图象可知,该函数在第一象限内y随x的增大而减小,
∴当时,,故B选项错误,不符合题意;
当时,则,
∴,故C选项错误,不符合题意;
当时,则,
∴,
由函数图象可知,该函数在第一象限内y随x的增大而减小,
∴当时,,故D选项正确,符合题意.
故选:D.
【点睛】本题考查了反比例函数的图象与应用,解题的关键是理解题意,掌握反比例函数的性质.
12.A
【分析】根据图象求出反比例函数解析式,再代入求值即可.
【详解】解:∵密度是体积的反比例函数,
∴设解析式为,把代入得,
,
解得,,解析式为,
把代入得,,
解得,,
故选:A.
【点睛】本题考查了反比例函数的应用,解题关键是根据图象上的坐标,求出反比例函数解析式.
13.C
【分析】根据图象即可判断A、B选项;根据图象可得当g时,的阻值为,则电路中的总电阻,再根据计算出电流,和A比较即可判断C选项;根据据计算出电流,和A比较即可判断D选项.
【详解】解:由图2可知,载盘台所载质量m越大,传感器的阻值越小,故A选项正确,不符合题意;
由图2可知,当g时,的阻值为,故B选项正确,不符合题意;
当g时,的阻值为,
电路中的总电阻,
∴,
∴提示器会发出提示音,故C选项错误,符合题意;
当时,
电路中的总电阻,
∴,
∴提示器会发出提示音,故D选项正确,不符合题意.
故选:C.
【点睛】本题主要考查函数与图象,理解题意,从图中获取需要的信息,并进行准确地计算是解题关键.
14.C
【分析】A.根据电压电流电阻,即可求解;
B.根据电压电流电阻,即可求解;
C.设,可求,进行判断即可;
D.若该电路的最小电阻值为,代入计算即可;
【详解】解:A.根据电压电流电阻,
蓄电池的电流,故不符合题意.
B.根据电压电流电阻,
蓄电池的电压值是,故不符合题意;
C.设,
将点代入得,
,
;
图中图象可以表示电流和电阻之间的函数关系,故符合题意;
D.若该电路的最小电阻值为,该电路能通过的最大电流是,故不符合题意;
故选:C.
【点睛】本题考查了反比例函数的应用,从实际问题中整理出反比例函数模型是解决此类问题的关键.
15.>
【分析】根据表格数据求得反比例函数解析式,根据反比例数的性质即可求解.
【详解】解:∵压强P与它的受力面积S成反比例函数关系,设,
依题意,
∴反比例数解析式为:,,
∴随的增大而减小,
∵,
∴,
故答案为:>.
【点睛】本题考查了反比例函数的应用,熟练掌握反比例函数的性质是解题的关键.
16.
【分析】根据反比例函数的性质,进行求解即可.
【详解】解:由图象可知,随着的增大而减小,当时,,
∴若使得通过滑动变阻器的电流不超过,则滑动变阻器阻值的范围是;
故答案为:.
【点睛】本题考查反比例函数的实际应用.熟练掌握反比例函数的性质,是解题的关键.
17.300
【分析】由表中数据可得销量与售价之间的函数解析式,根据题意有,将解析式代入解分式方程即可求解.
【详解】由表中数据得,
∴,则销量与售价之间的函数解析式为.
由题意,得,把代入,得,
解得,
经检验是原方程的根.
∴售价应定为300元.
故答案为:300.
【点睛】本题考查反比例函数的实际应用,分式方程的实际应用.理解题意,掌握利润=(售价-成本)×销售量是解答本题的关键.
18.
【分析】根据题意求得正比例函数解析式与反比例函数解析式,进而得出有效作用时间,即可求解.
【详解】解:依题意,时,喷洒消毒液时教室空气中的氯含量与时间成正比例,
设函数解析式为,
将点代入得,,解得:,
∴解析式为,当时,,
当时,与成反比例,设解析式为,
将点代入得,,
解得,
∴解析式为,当时,
∴此次消杀的有效作用时间是,
故答案为:.
【点睛】本题考查了正比例函数与反比例函数的应用,根据题意求得解析式是解题的关键.
19.(1)
(2)
(3)
(4)水池中的水至少要小时排完
【分析】(1)根据图示可知,当时间为小时时,排水量为,由此即可求解;
(2)运用待定系数法即可求解;
(3)把代入反比例函数,即可求解;
(4)根据题意可知,代入反比例函数即可求解.
【详解】(1)解:根据题意,设,
∵点在函数图象上,
∴蓄水量为.
(2)解:根据图示可知是反比例函数,设,点在函数图象上,
∴,解得,,
∴函数的解析式.
(3)解:当时,,
∴每小时的排水量应该是.
(4)解:∵,
∴,解得,,
∴水池中的水至少要小时排完.
【点睛】本题主要考查反比例函数的实际运用,理解反比例函数图象的意义,掌握待定系数法求解析式,代入求值计算是解题的关键.
20.(1)
(2)
(3)
【分析】(1)根据图像设正比例函数解析式为,根据图像可知函数解析式。再利用待定系数法即可求出恒定温度;
(2)根据图像可知整个图像由三部分组成:正比例函数、反比例函数、恒温,根据题意设函数解析式,利用待定系数法即可求出函数解析式;
(3)根据各时间段的函数解析式算出时的值,用小时减去这些时间即可.
【详解】(1)解:设直线的函数解析式为:,根据题意,
∴可得方程,
∴,
∴直线,
∵当时,
∴恒定温度为:.
(2)解:由(1)可知:正比例函数解析式为,
根据图像可知:,
设小时内函数解析式为:,根据题意,
可得方程:,
∴,
∴函数解析式为:,
∴小时函数解析式为:,
(3)解:∵当时,,
∴,
∵当时,,
∴,
∴在之间是气温是低于的,
∴气温低于的总时间为:,
∴气温高于的适宜温度是:.
【点睛】本题考查了一次函数、反比例函数和常函数解析式,解答时应注意临界点的应用.
21.C
【分析】根据题意可得动力F关于动力臂l的函数解析式为:,即可求得.
【详解】∵阻力阻力臂动力动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1000N和0.5m,
∴动力F关于动力臂l的函数解析式为:,
则.
故选:C.
【点睛】本题考查了实际问题与反比例函数,根据题意得出解析式是解题的关键.
22.A
【分析】根据实际意义,写出函数的解析式,根据函数的类型,以及自变量的取值范围即可进行判断.
【详解】解:根据题意有:;
故与之间的函数图象为反比例函数,且根据实际意义r、h应大于0,则其图象在第一象限.
故选:A.
【点睛】本题考查的是函数图象,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
23.C
【分析】根据表中数值求出反比例函数解析式,把代入解析式即可求出结果.
【详解】解:解:一定电压下通过导体的电流(A)和电阻之间成反比例函数,
设,
把时,代入得,
,
电流(A)和电阻之间的反比例函数解析式为,
当时,
即,
该电路中电阻不小于.
故选:C.
【点睛】本题主要考查了反比例函数的应用,求出反比例函数解析式是解决问题的关键.
24.C
【分析】由图像知加热时水温与通电时间成正比例关系,通电加热时水温每分钟上升,所以关系式为,进而可求得水温要从加热到所需要的时间.
【详解】解:由图可知水温要从加热到,水温与通电时间成正比例关系,关系式为 ,
当时,.
故选:C.
【点睛】本题考查一次函数的实际应用,熟练掌握相关知识是解题的关键.
25.
【分析】根据矩形的面积公式列出式子,再化为用的代数式表示即可求解.
【详解】解:∵长方形的面积为2,长与宽分别为x,y,
∴y与x的函数关系式为.
故答案为:.
【点睛】本题注意考查了反比例函数的应用,根据题意列出函数关系式是解题的关键.
26.乙
【分析】利用杠杆原理,得到力的大小与对杆的压力的作用点到支点的距离成反比关系,再通过比较力的大小,即可得到正确答案.
【详解】解:根据杠杆平衡原理:阻力阻力臂动力动力臂可得,
∵阻力阻力臂是个定值,即水桶的重力和水桶对杆的拉力的作用点到支点的杆长固定不变,
即:力的大小与对杆的压力的作用点到支点的距离成反比关系
∴动力越小,动力臂越大,即拉力越小,压力的作用点到支点的距离越远,
∵最小,
∴乙同学到支点的距离最远.
故答案为:乙.
【点睛】本题主要是考查了反比例函数的实际应用,利用反比关系,比较不同量的大小,熟练掌握反比关系,是求解该题的关键.
27.3
【分析】先根据待定系数法求得反比例函数解析式,再把ρ = 3.3代入计算即可.
【详解】解:设密度ρ与体积V的反比例函数解析式为ρ=,
把点(5,1.98)代入解ρ=,得k=9.9,
∴密度ρ与体积V的反比例函数解析式为ρ=,V>0.
当ρ = 3.3时,V==3,
即当ρ = 3.3 kg/m3时,相应的体积V是 3m3.
故答案为:3.
【点睛】本题主要考查反比例函数的性质和概念,解答此题的关键是找出变量之间的函数关系.
28.4000
【分析】直接利用函数图象得出函数解析式,进而求出答案.
【详解】设P=,把(0.5,2000)代入得:
k=1000,
故P=,
当S=0.25时,
P==4000(Pa).
故答案为:4000.
【点睛】此题主要考查了反比例函数的应用,正确求出函数解析是解题关键.
29.(1)关于的函数解析式为
(2)弹簧秤的示数的最小值为
【分析】(1)根据反比例函数的定义,运用待定系数法即可求解;
(2)根据反比例函数图形的性质即可求解.
【详解】(1)解:由题意设,把,代入,得,
∴关于的函数解析式为.
(2)解:由(1)可知,关于的函数解析式为,,是弹簧秤与中点的距离是,如图所示,
∵,
∴随的增大而减小,
∴把代入,得,
∴弹簧秤的示数的最小值为.
【点睛】本题主要考查反比例函数的运用,掌握待定系数法求反比例函数解析式,反比例函数图象的性质是解题的关键.
30.(1)
(2)3A
(3)用电器的可变电阻至少是
【分析】(1)利用待定系数法求解即可;
(2)把代入(1)所求解析式中求解即可;
(3)先求出当A时,,再由I随R的增大而减小,可知要使电流不能超过10A,则电阻要不低于.
【详解】(1)解:设反比例函数式,
∵把代入反比例函数式,
∴,
∴.
故答案为:.
(2)解:当,,
故答案为:3A;
(3)解:当A时,则,
∴,
∴用电器的可变电阻至少是.
【点睛】本题主要考查了反比例函数的实际应用,正确求出反比例函数解析式是解题的关键.
31.D
【分析】先找到要行驶的路程,再由等量关系“速度=路程÷时间”列出关系式即可.
【详解】解:由主桥长29.6千米,一辆汽车从主桥通过知行驶的路程为29.6千米,得到汽车的平均速度 v(千米/时)与时间 t(小时)的函数关系式为
故选:D
【点睛】本题考查了反比例函数在实际生活中的应用,重点是找出题中的等量关系.
32.D
【分析】根据题意求出动力F和动力臂l的函数关系式,再逐项判断即可.
【详解】解:A.∵阻力×阻力臂=动力×动力臂,已知阻力和阻力臂分别是和,
∴动力(单位:)关于动力臂(单位:)的函数解析式为:,故A项正确,不符合题意;
B.由,可知:F随l的增大而减小,故B正确,不符合题意;
C.当时,,故C项正确,不符合题意;
D.∵动力F和动力臂l均是正数的物理量,
∴的函数图象在第一象限,故D项错误,符合题意.
故选:D.
【点睛】本题考查了反比例函数的应用,弄清题意,正确分析各量间的关系是解题的关键.
33.B
【分析】设电流(单位:)与电阻(单位:)是反比例函数关系为,利用待定系数求出,再求出当,,最后根据反比例函数的增减性进行求解即可.
【详解】解:设电流(单位:)与电阻(单位:)是反比例函数关系为,
把点代入中得,,
∴,
∴,
当时,,解得,
∵,
∴电流I随电阻R的增大而减小,
∴限制电流不能超过,那么用电器可变电阻应控制的范围是,
故选B.
【点睛】本题主要考查了反比例函数的实际应用,正确求出是解题的关键.
34.B
【分析】根据函数图象可设,再将代入即可得出函数关系式,从而判断其他选项.
【详解】解:设,
图象过,
,
,
蓄电池的电压是,故①正确、②正确,
当时,(),故③错误;
当时,,
由图象知:当时,,故④正确;
故选:B.
【点睛】本题考查了待定系数法求反比例函数的解析式,关键是掌握函数图象上点的坐标必能满足解析式.
35.
【分析】先观察表中的数据,推导出力与动力臂的函数关系为反比例函数,再根据待定系数法求解即可.
【详解】解:观察表中的数据,满足,
则动力与动力臂的函数关系为反比例函数,
设这个函数的解析式为,
则,
∴个函数的解析式为,
当时,,
解得,
故答案为:.
【点睛】本题考查了反比例函数的应用,根据题意判断出动力与动力臂的函数关系为反比例函数是解决问题的关键.
36.④
【分析】由题意知,,则,根据反比例函数的图象与性质,反比例函数的实际应用对各说法进行判断即可.
【详解】解:由题意知,,则,,
∴F与l的积为定值,①正确,故不符合要求;
∵,
∴F随l的增大而减小,②正确,故不符合要求;
当,,③正确,故不符合要求;
由题意知,F关于l的函数图象位于第一象限,④错误,故符合要求;
故答案为:④.
【点睛】本题考查了反比例函数的实际应用,反比例函数的图象与性质.解题的关键在于对知识的熟练掌握与灵活运用.
37.
【分析】将点A代入可得k,求出时的t值,汽车所用时间应大于等于这个值.
【详解】解:由题意得,函数经过点
把代入,得
∴函数解析式为,
把代入,得,
∴汽车通过该路段最少需要小时.
故答案为:.
【点睛】本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
38.
【分析】设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,把点代入求出函数表达式,即可求解.
【详解】解:设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,
把点代入得:,
解得:,
∴设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,
当时,(小时),
当时,(小时),
(小时),
故答案为:.
【点睛】本题主要考查了求反比例函数的表达式,解题的关键是掌握用待定系数法求解函数表达式的方法和步骤.
39.(1)
(2)
【分析】(1)利用待定系数法求出函数表达式即可;
(2)把代入函数表达式求解即可.
【详解】(1)解:由题意设:,
把代入,得.
∴y关于x的函数表达式为;
(2)把代入,得.
∴小孔到蜡烛的距离为.
【点睛】此题考查了反比例函数,熟练掌握待定系数法是解题的关键.
40.(1),见解析
(2)3,m的实际意义为:当电阻R为,电流大小为
(3)该电路的可变电阻控制在不低于
【分析】(1)根据题意设,然后将代入求解记录;
(2)将代入求解即可;
(3)将代入求出R的值,然后结合图象求解即可.
【详解】(1)由于电流是电阻的反比例函数,
设,
∵图象过点,
∴,
∴I与R的函数表达式为;
(2)将代入得,,
∴解得,
∴m的实际意义为:当电阻R为,电流大小为;
(3)∵,
∴当时,,
∴当时,.
∴该电路的限制电流不能超过,那么该电路的可变电阻控制在不低于.
【点睛】此题考查了反比例函数的应用,解题的关键是求出函数表达式.
41.B
【分析】根据物理公式代入计算即可.
【详解】∵,压力合计,
∴,
故选B.
【点睛】本题考查了跨学科试题,反比例函数思想,熟练掌握物理公式是解题的关键.
42.D
【分析】根据反比例函数的性质,逐一进行判定即可.
【详解】解:∵近视眼镜的度数y(度)与镜片焦距x(m)的关系式为,
∴当x的值增大,y的值随之减小,
故A正确,不符合题意;
当时,,
故B正确,不符合题意;
当时,,
故C正确,不符合题意;
当时,,
∴(度),
即东东的眼镜度数下降了150度,
故D错误,符合题意.
故选:D.
【点睛】本题考查反比例函数的实际应用.熟练掌握反比例函数的性质,是解题的关键.
43.C
【分析】仔细观察表格,在坐标系中分别描出各点,并平滑曲线连接这些点,即可画出函数图像;观察所画图形,回想常见几种函数的图像特征,即可判断出函数类型,利用待定系数法求出函数关系式;把代入上面所得关系式求解,并根据函数的性质判断弹簧秤与O点的距离不断增大时的弹簧测力计示数变化情况.
【详解】解:由图像猜测y与x之间的函数关系为反比例函数.
所以设
把代入求得
∴
将其余各点代入验证均适合,
∴y与x的函数关系式为,
把代入得,
∴当弹簧测力计的示数为时,弹簧测力计与O点的距离是,
随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小.
故选:C.
【点睛】此题考查的是反比例函数的应用,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
44.C
【分析】由题意知,,整理得,可判断A的正误;根据的性质可知,随 的增大而增大,计算时,的值,进而可判断B的正误;根据定值电阻的阻值不变,可判断C的正误;当时,计算的值,进而可得的值,根据的性质,求的最大值,进而可判断D的正误.
【详解】解:由题意知,,
解得,
∴A正确,故不符合要求;
由可知,随 的增大而增大,
当时,的最大值为120(千克);
∴B正确,故不符合要求;
∵定值电阻的阻值不变,
∴C错误,故符合要求;
当时,(欧),
若定值电阻为40(欧),则(欧),
∵,
∴随 的增大而增大,的最大值为(伏),
∴D正确,故不符合要求;
故选:C.
【点睛】本题考查了一次函数与反比例函数的应用.解题的关键在于熟练掌握反比例函数的图象与性质.
45.丙
【分析】根据反比例函数图像与性质求解即可得到结论.
【详解】解:描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,设反比例函数表达式为,则令甲、乙、丙、丁,
过甲点作轴平行线交反比例函数于,过丙点作轴平行线交反比例函数于,如图所示:
由图可知,
、乙、、丁在反比例函数图像上,
根据题意可知优秀人数,则
①,即乙、丁两所学校优秀人数相同;
②,即甲学校优秀人数比乙、丁两所学校优秀人数少;
③,即丙学校优秀人数比乙、丁两所学校优秀人数多;
综上所述:甲学校优秀人数乙学校优秀人数丁学校优秀人数丙学校优秀人数,
在这次党史知识竞赛中成绩优秀人数最多的是丙学校,
故答案为:丙.
【点睛】本题考查反比例函数图像与性质的实际应用题,读懂题意,并熟练掌握反比例函数的图像与性质是解决问题的关键.
46.8
【分析】根据的解析式可求出点A的坐标,进而可得熏蒸完后的关系式,令,结合函数的性质可得有效时间.
【详解】解:当时,,
,
设熏蒸完后函数的关系式为:,
,
∴熏蒸完后函数的关系式为,
∵药物浓度不低于,
∴当时,,
当时,,
∴有效时长为:,
故答案为:8.
【点睛】本题考查了反比例函数及正比例函数的应用,解题的关键是能够从实际问题中抽象出反比例函数和正比例函数模型.
47. 12 9 17
【分析】(1)先确定的坐标,然后根据反比例函数即可确定k的值;
(2)观察发现,在反比例函数图像上的点,横纵坐标乘积相等,即可确定另一点;
(3)先分别求出横纵坐标的积,再从小到大排列,然后让k值位于第6个和第7个或第5个和第6个点横纵坐标的积之间,即可确定k的取值范围和k的整数值的个数.
【详解】解:(1)由图像可知,
∵函数的图象经过,
∴,即;
故答案为:12;
(2)由图像可知:,,,,,,,,,,,
∵过点,
∴,
观察,发现横纵坐标的乘积为,
∴;
故答案为:9;
(3)∵的横纵坐标积分别为:12,10,20,16,24,18,24,16,20,10,12,
∴将这11个点的横、纵坐标乘积从小到大排序为:10,10,12,12,16,16,18,20,20,24,24,
∵第5个数与第6个数相等,
∴要使这11个点分布在它的两侧,且一侧5个点一侧6个点,则k必须满足,
∴k可取的整数值为17.
故答案为:17.
【点睛】本题主要考查了反比例函数图像的特点,掌握反比例函数图像上的点的横纵坐标积等于k是解答本题的关键.
48.
【分析】根据一次函数图象上两点的坐标,利用待定系数法即可求出当时,水温与开机时间x的函数关系式;由点,利用待定系数法即可求出当时,水温与开机时间的函数关系式,再将代入该函数关系式中求出x值即可,由,将代入反比例函数关系式中求出y值即可得出结论.
【详解】解:当时,设水温与开机时间的函数关系为:,
依据题意,得,
解得:,
故此函数解析式为:;
在水温下降过程中,设水温y与开机时间x的函数关系式为:,
依据题意,得:,
解得:,
∴,
当时,,
解得:,
∵,
∴当时,.
故答案为:.
【点睛】本题考查了反比例函数的应用,解题的关键是根据点的坐标,利用待定系数法求出函数关系式.
49.(1)见解析
(2)y与x之间的函数关系式为.画出图象见解析
(3)销售单价x定为10元时,才能获得最大日销售利润,最大日销售利润为 48元
【分析】(1)建立坐标系直接描点即可;
(2)要确定y与x之间的函数关系式,通过观察表中数据,可以发现y与x的乘积是相同的,都是60,所以可知y与x成反比例,用待定系数法求解后再验证即可;
(3)先确定与的函数关系式,然后根据售价最高不超过10元/张,利用函数的增减性即可得出答案.
【详解】(1)解:建立平面直角坐标系描点,如图所示:
(2)解:由题意设y与x之间的函数关系式为(且k为常数),把代入,得,
将,,分别代入,均成立,
所以y与x之间的函数关系式为,
画出的图象如上图所示;
(3)解:,
当时,w随x的增大而增大,
又因为,
所以当时,,
所以,销售单价x定为10元时,才能获得最大日销售利润,最大日销售利润为 48元.
【点睛】本题主要考查了反比例函数的定义,待定系数法以及利用反比例关系式求最大值的问题,解题的关键是知道两个变量的乘法是定值时是反比例关系.
50.(1)图象见解析
(2)①②③
(3),②
【分析】(1)用光滑的曲线将点顺次连接起来即可;
(2)根据函数图象的增减性即可求解;
(3)①设鸡圈的一边长为,则另一边长为,再根据长方形周长公式即可求解;②根据“预算不超过750元”列不等式即可求解.
【详解】(1)解:函数图象如下所示:
(2)解:由函数图象可知,当时,y值随x的增大而减小,当时,y值随x的增大而增大,
因此若 , 则;若 , 则;若,则 ,
故答案为:①②③;
(3)解:①设鸡圈的一边长为,则另一边长为,
因此y与x之间的函数关系式为:;
②由题意知:,
整理得:,即,
解得.
【点睛】本题主要考查反比例函数的实际应用、从函数的图象获取信息、一元二次方程的应用等,解题的关键是能够从函数图象获取相关信息.
答案第1页,共2页
答案第1页,共2页
1.掌握用反比例函数解决实际问题
2.掌握反比例函数在其他学科中的应用
知识点 实际问题与反比例函数
【知识点】
知识点一、利用反比例函数解决实际问题
1.基本思路:建立函数模型,即在实际问题中求得函数解析式,然后应用函数的图象和性质等知识解决问题.
2.一般步骤如下:
(1)审清题意,根据常量、变量之间的关系,设出函数解析式,待定的系数用字母表示。(2)由题目中的已知条件,列出方程,求出待定系数.
(3)写出函数解析式,并注意解析式中变量的取值范围.
(4)利用函数解析式、函数的图象和性质等去解决问题.
知识点二、反比例函数在其他学科中的应用
1.当圆柱体的体积一定时,圆柱的底面积是高的反比例函数;
2.当工程总量一定时,做工时间是做工速度的反比例函数;
3.在使用杠杆时,如果阻力和阻力臂不变,则动力是动力臂的反比例函数;
【典型例题】
1.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压(单位:)是气体体积(单位:)的反比例函数:,能够反映两个变量和函数关系的图象是( )
A. B.
C. D.
2.小明设计了杠杆平衡实验:如图,取一根长质地均匀的木杆,用细绳绑在木杆的中点O处并将其吊起来,在左侧距离中点O处挂一个重的物体,在中点O右侧用一个弹簧测力计竖直向下拉,以保持木杆水平(动力×动力臂=阻力×阻力臂).改变弹簧测力计与中点O的距离L(单位:),观察并记录弹簧测力计的示数F(单位:N)有什么变化.小明根据实验得到的下列结论中,不正确的是( )
A.L与F的函数关系式为 B.当时,
C.当时, D.保持木杆水平,F的最小值为10
3.在一个可以改变体积的密闭容器内装有一定质量的气体,当改变容器的体积时,气体的密度也会随之改变,密度是体积的反比例函数,它的图象如图所示,根据图象可知,下列说法正确的是( )
A.密度随体积的增大而增大
B.密度和体积的关系式为
C.密度时,体积的范围为
D.体积时,密度的范围为
4.近视眼镜是一种为了矫正视力,让人们可以清晰看到远距离物体的凹透镜片.研究发现,近视眼镜的度数y(度)与镜片焦距的函数关系如图所示,则下列说法中错误的是( )
A.当x的值增大时,y的值随之减小
B.当焦距x为时,近视眼镜的度数y为500度
C.当焦距x为时,近视眼镜的度数y约300度
D.某人近视度数400度,镜片焦距应该调试为
5.如表记录了一组物理试验数据,已知当温度不变时,气球内气体的压强(单位:)是气体体积(单位:)的函数,则与的函数关系式是 .
(单位:)
(单位:)
6.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:)变化时,气体的密度(单位:)随之变化.已知密度与体积V是反比例函数关系,它的图象如图所示,当时,.
若,二氧化碳密度的变化范围
7.研究发现,近视眼镜的度数y(度)与镜片焦距x(米)成反比例函数关系,李阳佩戴的度近视镜片的焦距为米,经过一段时间的矫正治疗加之注意用眼健康,验光测得现在镜片焦距为米,则李阳的近视眼镜度数可以调整为 度.
8.为预防传染病,某校定期对教室进行“药熏消毒”.如图所示,药物燃烧阶段,教室内每立方米空气中的含药量与燃烧时间(分)成正比例;燃烧后,与成反比例.若,则的取值范围是 .
9.古希腊科学家阿基米德曾说“给我一个支点,我可以撬动地球”.后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力阻力臂动力动力臂(如图).小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别为和.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为2米时,撬动石头至少需要多大的力?
(2)若想使动力F不超过(1)中所用力的一半,则动力臂l至少要加长多少?
10.如图,取一根长米的质地均匀木杆,用细绳绑在木杆的中点处并将其吊起来,在中点的左侧距离中点处挂一个重牛的物体,在中点右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧称与中点的距离(单位:),看弹簧秤的示数(单位:牛,精确到牛)有什么变化,小慧在做此《数学活动》时,得到下表的数据:
牛
结果老师发现其中有一个数据明显有错误.
(1)你认为当______时所对应的数据是明显错误的;
(2)在已学过的函数中选择合适的模型求出与的函数关系式;
(3)若弹簧秤的最大量程是牛,求的取值范围.
【即学即练】
11.如图1是一盏亮度可调节的台灯,通过调节总电阻R来控制电流I实现灯光亮度的变化.电流与电阻之间的函数关系如图2所示.下列结论正确的是( )
A. B.当时, C.当时, D.当时,
12.在一个可以改变体积的密闭容器内装有一定质量的气体,当改变容器的体积时,气体的密度也会随之改变,密度是体积的反比例函数,它的图象如图所示,当气体的密度为时,体积是( ).
A.1 B.2 C.4 D.8
13.某自助餐厅餐桌上装有光盘仪,可用于“光盘行动”,光盘仪是一种质量电阻(图1中的传感器),的阻值随载盘台所载质量m的变化而变化(如图2),已知空载盘的质量为g,电源电压保持V不变,提示器的电阻恒为,则下列说法不正确的是( )
A.载盘台所载质量m越大,传感器的阻值越小
B.当g时,的阻值为
C.当g时,提示器不会发出提示音
D.当时,提示器会发出提示音
14.一定电压(单位:V)下电流和电阻之间成反比例关系,东东用一个蓄电池作为电源组装了一个电路如图1所示,通过实验,发现电流随着电阻值的变化而变化的一组数据如表格所示.
R(Ω) … 2 3 4 6 12 …
I(A) … 24 16 12 a 4 …
下列说法不正确的是( )
A.表中
B.这个蓄电池的电压值是48V
C.图2中图象可以表示电流I和电阻R之间的函数关系
D.若该电路的最小电阻值为1.5Ω,该电路能通过的最大电流是34A
15.物理学中,在压力F不变的情况下,某物体承受的压强P与它的受力面积S成反比例函数关系,则下表中压强与的大小关系为: .(填“”,“”或“”)
16.由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值R(始终保持),发现通过滑动变阻器的电流I与滑动变阻器的电阻R成反比例函数关系,它的图象如图所示,若使得通过滑动变阻器的电流不超过,则滑动变阻器阻值的范围是 .
17.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为元/双,要使该款运动鞋每天的销售利润达到元,则其售价应定为 元.
售价x(元/双) 200 250 300 400
销售量y(双) 30 24 20 15
18.为预防“新冠病毒”,学校对教室喷洒消毒液(含氯消毒剂)进行消杀,资料表明空气中氯含量不低于,才能有效杀灭新冠病毒.如图,喷洒消毒液时教室空气中的氯含量与时间成正比例,消毒液挥发时,与成反比例,则此次消杀的有效作用时间是 min.
19.如图所示是某一蓄水池每小时的排水量与排完水池中的水所用的时间之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)求出此函数的解析式;
(3)若要排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时排水量不超过,那么水池中的水至少要多少小时排完?
20.某水果生产基地在气温较低时,用装有恒温系统的大棚栽培一种新品种水果,如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度与时间之间的函数关系,其中线段表示恒温系统开启后阶段,双曲线的一部分表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)这个恒温系统设定的恒定温度为多少;
(2)求全天的温度与时间之间的函数关系式;
(3)若大棚内的温度低于不利于新品种水果的生长,问这天内,相对有利于水果生长的时间共多少小时?
题组A 基础过关练
(2023·辽宁大连·统考一模)
21.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力阻力臂动力动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1000N和0.5m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A. B. C. D.
(2023春·江苏·八年级专题练习)
22.已知圆柱的侧面积是,若圆柱底面半径为,高为,则关于的函数图象大致是( )
A. B. C. D.
(2023秋·河北张家口·九年级校考阶段练习)
23.一定电压下通过导体的电流I(A)和电阻R(Ω)之间成反比例函数,小明通过组合电路做实验时,发现电流I(A)随着电阻R(Ω)的变化而变化,其数据如下表所示.若在该电路中,电流表的最大量程是3A,为确保不超过电流表的最大量程,则该电路中电阻不小于( )
R(Ω) … 2 3 4 …
I(A) … 2.4 1.6 1.2 …
A.2Ω B.1.8Ω C.1.6Ω D.1.5Ω
(2022春·全国·九年级专题练习)
24.学校的自动饮水机,通电加热时水温每分钟上升,加热到时,自动停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则水温要从加热到,所需要的时间为( )
A. B. C. D.
(2023春·江苏苏州·八年级统考期中)
25.矩形的面积为2,两条邻边长分别为x,y,则y关于x的函数关系式为 .
(2022春·全国·九年级专题练习)
26.一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力、、、,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是 同学.
(2022秋·福建福州·九年级福建省福州第八中学校考阶段练习)
27.密闭容器内有一定质量的二氧化碳,在温度不变的情况下,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知密度ρ是体积V的反比例函数关系,它的图象如图所示,则当ρ = 3.3 kg/m3时,相应的体积V是 m3.
(2023·山西吕梁·校考模拟预测)
28.某物体对地面的压强P(Pa)与物体和地面的接触面积S(m2)成反比例函数关系(如图),当该物体与地面的接触面积为0.25m2时,该物体对地面的压强是 Pa.
(2023·浙江丽水·统考一模)
29.如图,取一根长的均匀木杆,用细绳绑在木杆的中点并将其吊起来.在中点的左侧挂一个物体,在中点的右侧用一个弹簧秤向下拉,使木杆处于水平状态.根据杠杆原理,当物体保持不动时,弹簧秤的示数(单位:)是(弹簧秤与中点的距离)(单位:)的反比例函数,当时,.
(1)求关于的函数表达式.
(2)移动弹簧秤的位置,若木杆仍处于水平状态,求弹簧秤的示数的最小值.
(2022春·全国·九年级专题练习)
30.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)这个反比例函数的解析式是 ().
(2)若使用时电阻,则电流I是
(3)如果以蓄电池为电源的用电器的电流不能超过10A,那么用电器的可变电阻至少是多少?
题组B 能力提升练
(2023春·八年级课时练习)
31.港珠澳大桥桥隧全长55千米,其中主桥长29.6千米,一辆汽车从主桥通过时,汽车的平均速度 v(千米/时)与时间 t(小时)的函数关系式为( )
A. B. C.v=29.6t D.
(2023·福建福州·统考一模)
32.公元前3世纪,古希腊科学家阿基米德发现了“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂,当用撬棍撬动一块石头时,发现阻力和阻力臂分别为和,关于动力F和动力臂l,下列说法错误的是( )
A.F与l的积为定值
B.F随l的增大而减小
C.当l为时,撬动石头至少需要的力
D.F关于l的函数图象位于第一、第三象限
(2023秋·山东威海·九年级统考期末)
33.某蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,其图象如图所示.若以此蓄电池为电源的用电器,其限制电流不超过,那么用电器可变电阻应控制的范围是( )
A. B. C. D.
(2023秋·河南开封·九年级统考期末)
34.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:)与电阻R(单位:)是反比例函数关系,它的图象如图所示,下列说法正确的个数是( )
①这个反比例函数解析式为;②蓄电池的电压是;③当时,;④当时,
A.4 B.3 C.2 D.1
(2023·山西长治·校联考二模)
35.某数学小组在“探究杠杆平衡条件”实验中固定阻力和阻力臂,得到了下表中的动力与动力臂的几组对应值,根据学习经验,下表中a的值为 .
… 1.5 2 3 4 5 6 …
… 8 6 4 3 a 2 …
(2023·山东菏泽·统考一模)
36.公元前3世纪,古希结科学家阿基米德发现了“杠杆原理”,杠杆平衡时,阻力×阻力臂动力×动力臂,当用撬棍撬动一块石头时,发现阻力和阻力臂分别为1200N和m,关于动力F和动力臂l:①F与l的积为定值;②F随l的增大而减小;③当l为1.5m时,撬动石头至少需要400N的力;④F关于l的函数图象位于第一、第三象限,上面四种说法错误的是 .
(2023秋·河南信阳·九年级统考期末)
37.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系,其图象为如图所示的一段曲线,且端点为和.若行驶速度不得超过60km/h,则汽车通过该路段最少需要 h?
(2023春·江苏·八年级专题练习)
38.青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差 小时.
(2023春·山西晋城·八年级统考期中)
39.如图,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:)是物距(小孔到蜡烛的距离)x(单位:)的反比例函数,当时,
(1)求y关于x的函数表达式;
(2)若火焰的像高为,求小孔到蜡烛的距离.
(2023·河南焦作·统考一模)
40.如图,某种品牌的电动车的蓄电池电压为定值,使用电源时,电流是电阻的反比例函数,其图象经过,两点.
(1)求I与R的函数表达式,并说明比例系数的实际意义;
(2)求m的值,并说明m的实际意义;
(3)如果以蓄电池为电源的用电器限制电流不得超过,那么用电器的可变电阻应控制在什么范围内?
题组C 培优拔尖练
(2023·江苏常州·统考二模)
41.一村民在清理鱼塘时不慎被困淤泥中,消防队员以门板作船进行救援,设人和门板对淤泥的压力合计,门板面积为,则人和门板对淤泥的压强和门板面积之间的函数关系式为( )
A. B. C. D.
(2023·河南周口·统考一模)
42.很多学生由于学习时间过长,用眼不科学,视力下降,国家“双减”政策的目标之一就是减轻学生的作业辅导,让学生提质增效,近视眼镜可以清晰看到远距离物体,它的镜片是凹透镜,研究发现,近视眼镜的度数y(度)与镜片焦距x(m)的关系式为.下列说法不正确的是( )
A.上述问题中,当x的值增大,y的值随之减小
B.当镜片焦距是0.2m时,近视眼镜的度数是500度
C.当近视眼镜的度数是400度时,镜片焦距是0.25m
D.东东原来佩量400度的近视眼镜,经过一段时间的矫正治疗加注意用眼健康,复查验光时,所配镜片焦距调整为0.4m,则东东的眼镜度数下降了200度
(2023·河南濮阳·统考一模)
43.如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点O的距离,观察弹簧测力计的示数的变化情况.实验数据记录如下表:
…… 10 15 20 25 30 ……
…… 45 30 22.5 18 15 ……
下列说法不正确的是( )
A.弹簧测力计的示数与支点O的距离之间关系的图像如图
B.y与x的函数关系式为
C.当弹簧测力计的示数为时,弹簧测力计与O点的距离是37.5
D.随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小
(2023·河南驻马店·校考二模)
44.一款简易电子秤的工作原理:一个装有踏板(踏板质量忽略不计)的可变电阻,与踏板人的质量m之间的函数关系式为,其图象如图1所示;图2的电路中,电源电压恒为12伏,定值电阻的阻值为60欧,接通开关,人站上踏板,电流表显示的读数为I安,该读数可以换算为人的质量m,电流表量程为0~0.2安(温馨提示:导体两端的电压U,导体的电阻R,通过导体的电流I,满足关系式),则下面结论错误的为( )
A.用含I的代数式表示为
B.电子体重秤可称的最大质量为120千克
C.当时,若电源电压U为12(伏),则定值电阻最小为70(欧)
D.当时,若定值电阻为40(欧),则电源电压U最大为10(伏)
(2023·山东临沂·统考一模)
45.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的学校是 .
(2023春·八年级课时练习)
46.为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物熏蒸消毒.消毒药物在一间教室内空气中的浓度y(单位:)与时间x(单位:)的函数关系如图所示:校医进行药物熏蒸时y与x的函数关系式为,药物熏蒸完成后y与x成反比例函数关系,两个函数图象的交点为.教室空气中的药物浓度不低于于时,对杀灭病毒有效.当时,本次消毒过程中有效杀灭病毒的时间为 min
(2023秋·河北保定·九年级统考期末)
47.如图是6个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角和凹入的角的顶点记作(n为1~11的整数),函数的图象为L.
(1)若L过点,则 ;
(2)若L过,则L一定过另一点,则 ;
(3)若L使得这些点分布在它的两侧,且一侧5个点一侧6个点,请写出符合要求的k的所有整数值: .
(2023·山东济南·一模)
48.饮水机中原有水的温度为,通电开机后,饮水机自动开始加热(此过程中,水温与开机时间分满足一次函数关系),当加热到时自动停止加热,随后水温开始下降(此过程中,水温与开机时间x分成反比例函数关系),当水温降至时,饮水机又自动开始加热,……如此循环下去(如图所示).那么开机后分钟时,水的温度是 .
(2022秋·九年级单元测试)
49.某商场出售一批进价为2元的贺卡,在市场营销中发现,此种贺卡的销售单价x(单位:元)与日销售量y(单位:张)之间有如下关系:
销售单价x(元) 3 4 5 6
日销售量y(张) 20 15 12 10
(1)根据表中数据在平面直角坐标系中描出实数对的对应点;
(2)确定y与x之间的函数关系式,并画出图象;
(3)设此种贺卡的日销售利润为w元,试求出w与x之间的函数关系式.若物价局规定此种贺卡的售价最高不超过10元/张,请你求出销售单价x定为多少元时,才能获得最大日销售利润?并求出最大日销售利润.
(2023春·河南南阳·八年级统考期中)
50.为了探索函数 的图象与性质,我们参照学习函数的过程与方法.
x … 1 1.5 2 3 4.5 6 9 …
y … 10 7.5 6.5 6 6.5 7.5 10 …
列表:
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
(1)观察所描出点的分布,用一条光滑的曲线将点顺次连接起来,作出函数图象.
(2)已知点(x ,y )、(x ,y )在函数图象上,结合表格和函数图象,回答下列问题(填“>”“=”或“<”):
①若 , 则;
②若 , 则;
③若,则
(3)某农户要用一些围栏建造一个的长方形鸡圈,设鸡圈的一边长为,所需围栏长度为.
①请直接写出y与x之间的函数关系式;
②若围栏的单价为50元/m,且该农户买围栏的预算不超过750元,在不考虑其他影响因素的情况下,鸡圈的一边长x应控制在什么范围内
试卷第2页,共2页
试卷第1页,共1页
参考答案:
1.B
【分析】根据实际意义以及函数的解析式,根据函数的类型,以及自变量的取值范围即可进行判断.
【详解】解:当m一定时,与V之间成反比例函数,则函数图象是双曲线,同时自变量是正数.
故选:B.
【点睛】此题主要考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
2.C
【分析】根据动力×动力臂=阻力×阻力臂,可得出即即可得出结论.
【详解】解:∵动力×动力臂=阻力×阻力臂,
故选项正确,不符合题意.
∴当时,,
故选项正确,不符合题意.
∴当时,,
∴故选项错误,符合题意.
∵一根长质地均匀的木杆,用细绳绑在木杆的中点O处并将其吊起来,
∴右侧最长为,
故选项正确,不符合题意.
故选:
【点睛】本题主要考查了反比例函数与实际问题的综合,熟练掌握反比例函数的性质是解此题的关键.
3.C
【分析】求得反比例函数的关系式,根据反比例函数的性质解答即可.
【详解】解:观察图象,密度是体积的反比例函数,且经过点,
设反比例函数的关系式为,则,
∴函数关系式为,
A、密度随体积的增大而减少,原说法错误,本选项不符合题意;
B、密度和体积的关系式为,原说法错误,本选项不符合题意;
C、密度时,体积的范围为,正确,,本选项符合题意;
D、体积时,密度的范围为,原说法错误,本选项不符合题意;
故选:C.
【点睛】本题考查了反比例函数的应用,利用待定系数法求得比例函数的关系式是解题的关键.
4.D
【分析】根据反比例函数的性质可以判断A;利用已知解析式代入相关数据可以判断B,C,D.
【详解】∵近视眼镜的度数y(度)与镜片焦距的关系式为,
∴当x的值增大时,y的值随之减小,故A正确,不符合题意;
将代入,y值为500,故B正确,不符合题意;
将.代入,y值约为333,故C正确,不符合题意;
将代入,x值为0.25,故D错误,符合题意.
故选D.
【点睛】本题考查了反比例函数的应用,正确利用反比例函数的性质是解题关键.
5.
【分析】观察表格发现,从而确定两个变量之间的关系即可.
【详解】解:观察发现:,
故与的函数关系式为,
故答案为:.
【点睛】本题考查了反比例函数的应用,解题的关键是能够观察表格并发现两个变量的乘积为常数,难度不大.
6.
【分析】观察函数图像,根据函数图像上点的坐标,利用待定系数法可求出反比例函数的解析式,再利用反比例函数图像上点的坐标特征,即可求出答案.
【详解】解:∵密度与体积V是反比例函数关系,
∴设,
∵当时,,
∴,
∴,
∴密度关于体积V的函数解析式为:;
观察函数图象可知,随V的增大而减小,
当时,,
当时,,
∴当时,
即二氧化碳密度的变化范围是,
故答案为:.
【点睛】本题考查反比例函数的实际应用,掌握反比例函数图象的性质是解题的关键.
7.
【分析】设函数为,将度近视镜片的焦距为米代入求出k,再将米代入求解即可得到答案;
【详解】解:设函数为,将度近视镜片的焦距为米代入得,、
,解得:,
∴,
将代入求解可得,
,
故答案为:;
【点睛】本题考查待定系数法求解析式及函数值,解题的关键是根据题意找点代入.
8.
【分析】由函数图象得出相应函数关系式,再根据题目要求求出x的取值范围即可;
【详解】解:函数图象可知,
燃烧时,与成正比例函数: ,
将代入得,即,
∴,
燃烧后,与成反比例函数:,
将代入得,即,
∴,
∵,
∴即;即,
∴的取值范围是.
故答案为:.
【点睛】本题主要考查正比例函数、反比例函数的应用,正确理解题意并列出函数关系式是解题的关键.
9.(1)动力F与动力臂l的函数关系为,动力臂为2米时,撬动石头至少需要的力;
(2)动力臂至少要加长.
【分析】(1)直接利用:阻力阻力臂动力动力臂,进而得出F与l之间的关系;
(2)直接利用动力F不超过题(1)中所用力的一半,进而得出l的值.
【详解】(1)解:由题意可得:,
则,
当动力臂为2米时,
则撬动石头至少需要:,
答:动力F与动力臂l的函数关系为,动力臂为2米时,撬动石头至少需要的力;
(2)解:当动力F不超过题(1)中所用力的一半,即,
则,
解得:,
即动力臂至少要加长,
答:动力臂至少要加长.
【点睛】此题主要考查了反比例函数的应用,正确得出F与l之间的关系是解题关键.
10.(1);
(2);
(3).
【分析】(1)根据表格数据,可发现与的乘积为定值,从而可得答案;
(2)根据=,可得与的函数解析式;
(3)根据弹簧秤的最大量程是牛,即可得到结论.
【详解】(1)解:根据表格数据可知 ,
当时,牛,所以表格中数据错了,
故答案为:15;
(2)解:表格数据知.
F与L的函数关系式为:;
(3)解:当牛时,由,得,根据反比例函数的图象与性质可得,
由题意可知,L的取值范围是.
【点睛】本题考查了反比例函数的应用,解答本题的关键是仔细观察表格,得出F与L的积为定值,从而得出函数关系式.
11.D
【分析】由图象可知,电流与电阻之间满足反比例函数关系,设电流与电阻之间的函数关系为,根据点在函数的图象上得,进行计算得电流与电阻之间的函数关系为,当时,则,解得,由函数图象可知,该函数在第一象限内y随x的增大而减小,则当时,;当时,则,得;当时,则,计算得,由函数图象可知,该函数在第一象限内y随x的增大而减小,当时,;综上,即可得.
【详解】解:由图象可知,电流与电阻之间满足反比例函数关系,
设电流与电阻之间的函数关系为,
∵点在函数的图象上,
∴,
解得:,
∴电流与电阻之间的函数关系为,故A选项错误,不符合题意;
当时,则,
∴,
由函数图象可知,该函数在第一象限内y随x的增大而减小,
∴当时,,故B选项错误,不符合题意;
当时,则,
∴,故C选项错误,不符合题意;
当时,则,
∴,
由函数图象可知,该函数在第一象限内y随x的增大而减小,
∴当时,,故D选项正确,符合题意.
故选:D.
【点睛】本题考查了反比例函数的图象与应用,解题的关键是理解题意,掌握反比例函数的性质.
12.A
【分析】根据图象求出反比例函数解析式,再代入求值即可.
【详解】解:∵密度是体积的反比例函数,
∴设解析式为,把代入得,
,
解得,,解析式为,
把代入得,,
解得,,
故选:A.
【点睛】本题考查了反比例函数的应用,解题关键是根据图象上的坐标,求出反比例函数解析式.
13.C
【分析】根据图象即可判断A、B选项;根据图象可得当g时,的阻值为,则电路中的总电阻,再根据计算出电流,和A比较即可判断C选项;根据据计算出电流,和A比较即可判断D选项.
【详解】解:由图2可知,载盘台所载质量m越大,传感器的阻值越小,故A选项正确,不符合题意;
由图2可知,当g时,的阻值为,故B选项正确,不符合题意;
当g时,的阻值为,
电路中的总电阻,
∴,
∴提示器会发出提示音,故C选项错误,符合题意;
当时,
电路中的总电阻,
∴,
∴提示器会发出提示音,故D选项正确,不符合题意.
故选:C.
【点睛】本题主要考查函数与图象,理解题意,从图中获取需要的信息,并进行准确地计算是解题关键.
14.C
【分析】A.根据电压电流电阻,即可求解;
B.根据电压电流电阻,即可求解;
C.设,可求,进行判断即可;
D.若该电路的最小电阻值为,代入计算即可;
【详解】解:A.根据电压电流电阻,
蓄电池的电流,故不符合题意.
B.根据电压电流电阻,
蓄电池的电压值是,故不符合题意;
C.设,
将点代入得,
,
;
图中图象可以表示电流和电阻之间的函数关系,故符合题意;
D.若该电路的最小电阻值为,该电路能通过的最大电流是,故不符合题意;
故选:C.
【点睛】本题考查了反比例函数的应用,从实际问题中整理出反比例函数模型是解决此类问题的关键.
15.>
【分析】根据表格数据求得反比例函数解析式,根据反比例数的性质即可求解.
【详解】解:∵压强P与它的受力面积S成反比例函数关系,设,
依题意,
∴反比例数解析式为:,,
∴随的增大而减小,
∵,
∴,
故答案为:>.
【点睛】本题考查了反比例函数的应用,熟练掌握反比例函数的性质是解题的关键.
16.
【分析】根据反比例函数的性质,进行求解即可.
【详解】解:由图象可知,随着的增大而减小,当时,,
∴若使得通过滑动变阻器的电流不超过,则滑动变阻器阻值的范围是;
故答案为:.
【点睛】本题考查反比例函数的实际应用.熟练掌握反比例函数的性质,是解题的关键.
17.300
【分析】由表中数据可得销量与售价之间的函数解析式,根据题意有,将解析式代入解分式方程即可求解.
【详解】由表中数据得,
∴,则销量与售价之间的函数解析式为.
由题意,得,把代入,得,
解得,
经检验是原方程的根.
∴售价应定为300元.
故答案为:300.
【点睛】本题考查反比例函数的实际应用,分式方程的实际应用.理解题意,掌握利润=(售价-成本)×销售量是解答本题的关键.
18.
【分析】根据题意求得正比例函数解析式与反比例函数解析式,进而得出有效作用时间,即可求解.
【详解】解:依题意,时,喷洒消毒液时教室空气中的氯含量与时间成正比例,
设函数解析式为,
将点代入得,,解得:,
∴解析式为,当时,,
当时,与成反比例,设解析式为,
将点代入得,,
解得,
∴解析式为,当时,
∴此次消杀的有效作用时间是,
故答案为:.
【点睛】本题考查了正比例函数与反比例函数的应用,根据题意求得解析式是解题的关键.
19.(1)
(2)
(3)
(4)水池中的水至少要小时排完
【分析】(1)根据图示可知,当时间为小时时,排水量为,由此即可求解;
(2)运用待定系数法即可求解;
(3)把代入反比例函数,即可求解;
(4)根据题意可知,代入反比例函数即可求解.
【详解】(1)解:根据题意,设,
∵点在函数图象上,
∴蓄水量为.
(2)解:根据图示可知是反比例函数,设,点在函数图象上,
∴,解得,,
∴函数的解析式.
(3)解:当时,,
∴每小时的排水量应该是.
(4)解:∵,
∴,解得,,
∴水池中的水至少要小时排完.
【点睛】本题主要考查反比例函数的实际运用,理解反比例函数图象的意义,掌握待定系数法求解析式,代入求值计算是解题的关键.
20.(1)
(2)
(3)
【分析】(1)根据图像设正比例函数解析式为,根据图像可知函数解析式。再利用待定系数法即可求出恒定温度;
(2)根据图像可知整个图像由三部分组成:正比例函数、反比例函数、恒温,根据题意设函数解析式,利用待定系数法即可求出函数解析式;
(3)根据各时间段的函数解析式算出时的值,用小时减去这些时间即可.
【详解】(1)解:设直线的函数解析式为:,根据题意,
∴可得方程,
∴,
∴直线,
∵当时,
∴恒定温度为:.
(2)解:由(1)可知:正比例函数解析式为,
根据图像可知:,
设小时内函数解析式为:,根据题意,
可得方程:,
∴,
∴函数解析式为:,
∴小时函数解析式为:,
(3)解:∵当时,,
∴,
∵当时,,
∴,
∴在之间是气温是低于的,
∴气温低于的总时间为:,
∴气温高于的适宜温度是:.
【点睛】本题考查了一次函数、反比例函数和常函数解析式,解答时应注意临界点的应用.
21.C
【分析】根据题意可得动力F关于动力臂l的函数解析式为:,即可求得.
【详解】∵阻力阻力臂动力动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1000N和0.5m,
∴动力F关于动力臂l的函数解析式为:,
则.
故选:C.
【点睛】本题考查了实际问题与反比例函数,根据题意得出解析式是解题的关键.
22.A
【分析】根据实际意义,写出函数的解析式,根据函数的类型,以及自变量的取值范围即可进行判断.
【详解】解:根据题意有:;
故与之间的函数图象为反比例函数,且根据实际意义r、h应大于0,则其图象在第一象限.
故选:A.
【点睛】本题考查的是函数图象,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
23.C
【分析】根据表中数值求出反比例函数解析式,把代入解析式即可求出结果.
【详解】解:解:一定电压下通过导体的电流(A)和电阻之间成反比例函数,
设,
把时,代入得,
,
电流(A)和电阻之间的反比例函数解析式为,
当时,
即,
该电路中电阻不小于.
故选:C.
【点睛】本题主要考查了反比例函数的应用,求出反比例函数解析式是解决问题的关键.
24.C
【分析】由图像知加热时水温与通电时间成正比例关系,通电加热时水温每分钟上升,所以关系式为,进而可求得水温要从加热到所需要的时间.
【详解】解:由图可知水温要从加热到,水温与通电时间成正比例关系,关系式为 ,
当时,.
故选:C.
【点睛】本题考查一次函数的实际应用,熟练掌握相关知识是解题的关键.
25.
【分析】根据矩形的面积公式列出式子,再化为用的代数式表示即可求解.
【详解】解:∵长方形的面积为2,长与宽分别为x,y,
∴y与x的函数关系式为.
故答案为:.
【点睛】本题注意考查了反比例函数的应用,根据题意列出函数关系式是解题的关键.
26.乙
【分析】利用杠杆原理,得到力的大小与对杆的压力的作用点到支点的距离成反比关系,再通过比较力的大小,即可得到正确答案.
【详解】解:根据杠杆平衡原理:阻力阻力臂动力动力臂可得,
∵阻力阻力臂是个定值,即水桶的重力和水桶对杆的拉力的作用点到支点的杆长固定不变,
即:力的大小与对杆的压力的作用点到支点的距离成反比关系
∴动力越小,动力臂越大,即拉力越小,压力的作用点到支点的距离越远,
∵最小,
∴乙同学到支点的距离最远.
故答案为:乙.
【点睛】本题主要是考查了反比例函数的实际应用,利用反比关系,比较不同量的大小,熟练掌握反比关系,是求解该题的关键.
27.3
【分析】先根据待定系数法求得反比例函数解析式,再把ρ = 3.3代入计算即可.
【详解】解:设密度ρ与体积V的反比例函数解析式为ρ=,
把点(5,1.98)代入解ρ=,得k=9.9,
∴密度ρ与体积V的反比例函数解析式为ρ=,V>0.
当ρ = 3.3时,V==3,
即当ρ = 3.3 kg/m3时,相应的体积V是 3m3.
故答案为:3.
【点睛】本题主要考查反比例函数的性质和概念,解答此题的关键是找出变量之间的函数关系.
28.4000
【分析】直接利用函数图象得出函数解析式,进而求出答案.
【详解】设P=,把(0.5,2000)代入得:
k=1000,
故P=,
当S=0.25时,
P==4000(Pa).
故答案为:4000.
【点睛】此题主要考查了反比例函数的应用,正确求出函数解析是解题关键.
29.(1)关于的函数解析式为
(2)弹簧秤的示数的最小值为
【分析】(1)根据反比例函数的定义,运用待定系数法即可求解;
(2)根据反比例函数图形的性质即可求解.
【详解】(1)解:由题意设,把,代入,得,
∴关于的函数解析式为.
(2)解:由(1)可知,关于的函数解析式为,,是弹簧秤与中点的距离是,如图所示,
∵,
∴随的增大而减小,
∴把代入,得,
∴弹簧秤的示数的最小值为.
【点睛】本题主要考查反比例函数的运用,掌握待定系数法求反比例函数解析式,反比例函数图象的性质是解题的关键.
30.(1)
(2)3A
(3)用电器的可变电阻至少是
【分析】(1)利用待定系数法求解即可;
(2)把代入(1)所求解析式中求解即可;
(3)先求出当A时,,再由I随R的增大而减小,可知要使电流不能超过10A,则电阻要不低于.
【详解】(1)解:设反比例函数式,
∵把代入反比例函数式,
∴,
∴.
故答案为:.
(2)解:当,,
故答案为:3A;
(3)解:当A时,则,
∴,
∴用电器的可变电阻至少是.
【点睛】本题主要考查了反比例函数的实际应用,正确求出反比例函数解析式是解题的关键.
31.D
【分析】先找到要行驶的路程,再由等量关系“速度=路程÷时间”列出关系式即可.
【详解】解:由主桥长29.6千米,一辆汽车从主桥通过知行驶的路程为29.6千米,得到汽车的平均速度 v(千米/时)与时间 t(小时)的函数关系式为
故选:D
【点睛】本题考查了反比例函数在实际生活中的应用,重点是找出题中的等量关系.
32.D
【分析】根据题意求出动力F和动力臂l的函数关系式,再逐项判断即可.
【详解】解:A.∵阻力×阻力臂=动力×动力臂,已知阻力和阻力臂分别是和,
∴动力(单位:)关于动力臂(单位:)的函数解析式为:,故A项正确,不符合题意;
B.由,可知:F随l的增大而减小,故B正确,不符合题意;
C.当时,,故C项正确,不符合题意;
D.∵动力F和动力臂l均是正数的物理量,
∴的函数图象在第一象限,故D项错误,符合题意.
故选:D.
【点睛】本题考查了反比例函数的应用,弄清题意,正确分析各量间的关系是解题的关键.
33.B
【分析】设电流(单位:)与电阻(单位:)是反比例函数关系为,利用待定系数求出,再求出当,,最后根据反比例函数的增减性进行求解即可.
【详解】解:设电流(单位:)与电阻(单位:)是反比例函数关系为,
把点代入中得,,
∴,
∴,
当时,,解得,
∵,
∴电流I随电阻R的增大而减小,
∴限制电流不能超过,那么用电器可变电阻应控制的范围是,
故选B.
【点睛】本题主要考查了反比例函数的实际应用,正确求出是解题的关键.
34.B
【分析】根据函数图象可设,再将代入即可得出函数关系式,从而判断其他选项.
【详解】解:设,
图象过,
,
,
蓄电池的电压是,故①正确、②正确,
当时,(),故③错误;
当时,,
由图象知:当时,,故④正确;
故选:B.
【点睛】本题考查了待定系数法求反比例函数的解析式,关键是掌握函数图象上点的坐标必能满足解析式.
35.
【分析】先观察表中的数据,推导出力与动力臂的函数关系为反比例函数,再根据待定系数法求解即可.
【详解】解:观察表中的数据,满足,
则动力与动力臂的函数关系为反比例函数,
设这个函数的解析式为,
则,
∴个函数的解析式为,
当时,,
解得,
故答案为:.
【点睛】本题考查了反比例函数的应用,根据题意判断出动力与动力臂的函数关系为反比例函数是解决问题的关键.
36.④
【分析】由题意知,,则,根据反比例函数的图象与性质,反比例函数的实际应用对各说法进行判断即可.
【详解】解:由题意知,,则,,
∴F与l的积为定值,①正确,故不符合要求;
∵,
∴F随l的增大而减小,②正确,故不符合要求;
当,,③正确,故不符合要求;
由题意知,F关于l的函数图象位于第一象限,④错误,故符合要求;
故答案为:④.
【点睛】本题考查了反比例函数的实际应用,反比例函数的图象与性质.解题的关键在于对知识的熟练掌握与灵活运用.
37.
【分析】将点A代入可得k,求出时的t值,汽车所用时间应大于等于这个值.
【详解】解:由题意得,函数经过点
把代入,得
∴函数解析式为,
把代入,得,
∴汽车通过该路段最少需要小时.
故答案为:.
【点睛】本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
38.
【分析】设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,把点代入求出函数表达式,即可求解.
【详解】解:设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,
把点代入得:,
解得:,
∴设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,
当时,(小时),
当时,(小时),
(小时),
故答案为:.
【点睛】本题主要考查了求反比例函数的表达式,解题的关键是掌握用待定系数法求解函数表达式的方法和步骤.
39.(1)
(2)
【分析】(1)利用待定系数法求出函数表达式即可;
(2)把代入函数表达式求解即可.
【详解】(1)解:由题意设:,
把代入,得.
∴y关于x的函数表达式为;
(2)把代入,得.
∴小孔到蜡烛的距离为.
【点睛】此题考查了反比例函数,熟练掌握待定系数法是解题的关键.
40.(1),见解析
(2)3,m的实际意义为:当电阻R为,电流大小为
(3)该电路的可变电阻控制在不低于
【分析】(1)根据题意设,然后将代入求解记录;
(2)将代入求解即可;
(3)将代入求出R的值,然后结合图象求解即可.
【详解】(1)由于电流是电阻的反比例函数,
设,
∵图象过点,
∴,
∴I与R的函数表达式为;
(2)将代入得,,
∴解得,
∴m的实际意义为:当电阻R为,电流大小为;
(3)∵,
∴当时,,
∴当时,.
∴该电路的限制电流不能超过,那么该电路的可变电阻控制在不低于.
【点睛】此题考查了反比例函数的应用,解题的关键是求出函数表达式.
41.B
【分析】根据物理公式代入计算即可.
【详解】∵,压力合计,
∴,
故选B.
【点睛】本题考查了跨学科试题,反比例函数思想,熟练掌握物理公式是解题的关键.
42.D
【分析】根据反比例函数的性质,逐一进行判定即可.
【详解】解:∵近视眼镜的度数y(度)与镜片焦距x(m)的关系式为,
∴当x的值增大,y的值随之减小,
故A正确,不符合题意;
当时,,
故B正确,不符合题意;
当时,,
故C正确,不符合题意;
当时,,
∴(度),
即东东的眼镜度数下降了150度,
故D错误,符合题意.
故选:D.
【点睛】本题考查反比例函数的实际应用.熟练掌握反比例函数的性质,是解题的关键.
43.C
【分析】仔细观察表格,在坐标系中分别描出各点,并平滑曲线连接这些点,即可画出函数图像;观察所画图形,回想常见几种函数的图像特征,即可判断出函数类型,利用待定系数法求出函数关系式;把代入上面所得关系式求解,并根据函数的性质判断弹簧秤与O点的距离不断增大时的弹簧测力计示数变化情况.
【详解】解:由图像猜测y与x之间的函数关系为反比例函数.
所以设
把代入求得
∴
将其余各点代入验证均适合,
∴y与x的函数关系式为,
把代入得,
∴当弹簧测力计的示数为时,弹簧测力计与O点的距离是,
随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小.
故选:C.
【点睛】此题考查的是反比例函数的应用,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
44.C
【分析】由题意知,,整理得,可判断A的正误;根据的性质可知,随 的增大而增大,计算时,的值,进而可判断B的正误;根据定值电阻的阻值不变,可判断C的正误;当时,计算的值,进而可得的值,根据的性质,求的最大值,进而可判断D的正误.
【详解】解:由题意知,,
解得,
∴A正确,故不符合要求;
由可知,随 的增大而增大,
当时,的最大值为120(千克);
∴B正确,故不符合要求;
∵定值电阻的阻值不变,
∴C错误,故符合要求;
当时,(欧),
若定值电阻为40(欧),则(欧),
∵,
∴随 的增大而增大,的最大值为(伏),
∴D正确,故不符合要求;
故选:C.
【点睛】本题考查了一次函数与反比例函数的应用.解题的关键在于熟练掌握反比例函数的图象与性质.
45.丙
【分析】根据反比例函数图像与性质求解即可得到结论.
【详解】解:描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,设反比例函数表达式为,则令甲、乙、丙、丁,
过甲点作轴平行线交反比例函数于,过丙点作轴平行线交反比例函数于,如图所示:
由图可知,
、乙、、丁在反比例函数图像上,
根据题意可知优秀人数,则
①,即乙、丁两所学校优秀人数相同;
②,即甲学校优秀人数比乙、丁两所学校优秀人数少;
③,即丙学校优秀人数比乙、丁两所学校优秀人数多;
综上所述:甲学校优秀人数乙学校优秀人数丁学校优秀人数丙学校优秀人数,
在这次党史知识竞赛中成绩优秀人数最多的是丙学校,
故答案为:丙.
【点睛】本题考查反比例函数图像与性质的实际应用题,读懂题意,并熟练掌握反比例函数的图像与性质是解决问题的关键.
46.8
【分析】根据的解析式可求出点A的坐标,进而可得熏蒸完后的关系式,令,结合函数的性质可得有效时间.
【详解】解:当时,,
,
设熏蒸完后函数的关系式为:,
,
∴熏蒸完后函数的关系式为,
∵药物浓度不低于,
∴当时,,
当时,,
∴有效时长为:,
故答案为:8.
【点睛】本题考查了反比例函数及正比例函数的应用,解题的关键是能够从实际问题中抽象出反比例函数和正比例函数模型.
47. 12 9 17
【分析】(1)先确定的坐标,然后根据反比例函数即可确定k的值;
(2)观察发现,在反比例函数图像上的点,横纵坐标乘积相等,即可确定另一点;
(3)先分别求出横纵坐标的积,再从小到大排列,然后让k值位于第6个和第7个或第5个和第6个点横纵坐标的积之间,即可确定k的取值范围和k的整数值的个数.
【详解】解:(1)由图像可知,
∵函数的图象经过,
∴,即;
故答案为:12;
(2)由图像可知:,,,,,,,,,,,
∵过点,
∴,
观察,发现横纵坐标的乘积为,
∴;
故答案为:9;
(3)∵的横纵坐标积分别为:12,10,20,16,24,18,24,16,20,10,12,
∴将这11个点的横、纵坐标乘积从小到大排序为:10,10,12,12,16,16,18,20,20,24,24,
∵第5个数与第6个数相等,
∴要使这11个点分布在它的两侧,且一侧5个点一侧6个点,则k必须满足,
∴k可取的整数值为17.
故答案为:17.
【点睛】本题主要考查了反比例函数图像的特点,掌握反比例函数图像上的点的横纵坐标积等于k是解答本题的关键.
48.
【分析】根据一次函数图象上两点的坐标,利用待定系数法即可求出当时,水温与开机时间x的函数关系式;由点,利用待定系数法即可求出当时,水温与开机时间的函数关系式,再将代入该函数关系式中求出x值即可,由,将代入反比例函数关系式中求出y值即可得出结论.
【详解】解:当时,设水温与开机时间的函数关系为:,
依据题意,得,
解得:,
故此函数解析式为:;
在水温下降过程中,设水温y与开机时间x的函数关系式为:,
依据题意,得:,
解得:,
∴,
当时,,
解得:,
∵,
∴当时,.
故答案为:.
【点睛】本题考查了反比例函数的应用,解题的关键是根据点的坐标,利用待定系数法求出函数关系式.
49.(1)见解析
(2)y与x之间的函数关系式为.画出图象见解析
(3)销售单价x定为10元时,才能获得最大日销售利润,最大日销售利润为 48元
【分析】(1)建立坐标系直接描点即可;
(2)要确定y与x之间的函数关系式,通过观察表中数据,可以发现y与x的乘积是相同的,都是60,所以可知y与x成反比例,用待定系数法求解后再验证即可;
(3)先确定与的函数关系式,然后根据售价最高不超过10元/张,利用函数的增减性即可得出答案.
【详解】(1)解:建立平面直角坐标系描点,如图所示:
(2)解:由题意设y与x之间的函数关系式为(且k为常数),把代入,得,
将,,分别代入,均成立,
所以y与x之间的函数关系式为,
画出的图象如上图所示;
(3)解:,
当时,w随x的增大而增大,
又因为,
所以当时,,
所以,销售单价x定为10元时,才能获得最大日销售利润,最大日销售利润为 48元.
【点睛】本题主要考查了反比例函数的定义,待定系数法以及利用反比例关系式求最大值的问题,解题的关键是知道两个变量的乘法是定值时是反比例关系.
50.(1)图象见解析
(2)①②③
(3),②
【分析】(1)用光滑的曲线将点顺次连接起来即可;
(2)根据函数图象的增减性即可求解;
(3)①设鸡圈的一边长为,则另一边长为,再根据长方形周长公式即可求解;②根据“预算不超过750元”列不等式即可求解.
【详解】(1)解:函数图象如下所示:
(2)解:由函数图象可知,当时,y值随x的增大而减小,当时,y值随x的增大而增大,
因此若 , 则;若 , 则;若,则 ,
故答案为:①②③;
(3)解:①设鸡圈的一边长为,则另一边长为,
因此y与x之间的函数关系式为:;
②由题意知:,
整理得:,即,
解得.
【点睛】本题主要考查反比例函数的实际应用、从函数的图象获取信息、一元二次方程的应用等,解题的关键是能够从函数图象获取相关信息.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
