浙教版数学九年级上册 4.5相似三角形的性质及其应用(第3课时 )习题课件 16张PPT
文档属性
| 名称 | 浙教版数学九年级上册 4.5相似三角形的性质及其应用(第3课时 )习题课件 16张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 862.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
4.5 相似三角形的性质及其应用
第3课时 相似三角形的应用
学习目标
进一步掌握和理解相似三角形的性质.
能运用相似三角形的有关性质解决简单的实际问题.
知识回顾
迄今为止,我们都学习了哪些相似三角形的性质?
1.相似三角形的对应角相等,对应边成比例.
2.相似三角形对应线段的比都等于相似比.
3.相似三角形的周长之比等于相似比;
相似三角形的面积之比等于相似比的平方.
下面我们来看相似三角形性质的一些实际应用.
典例精讲
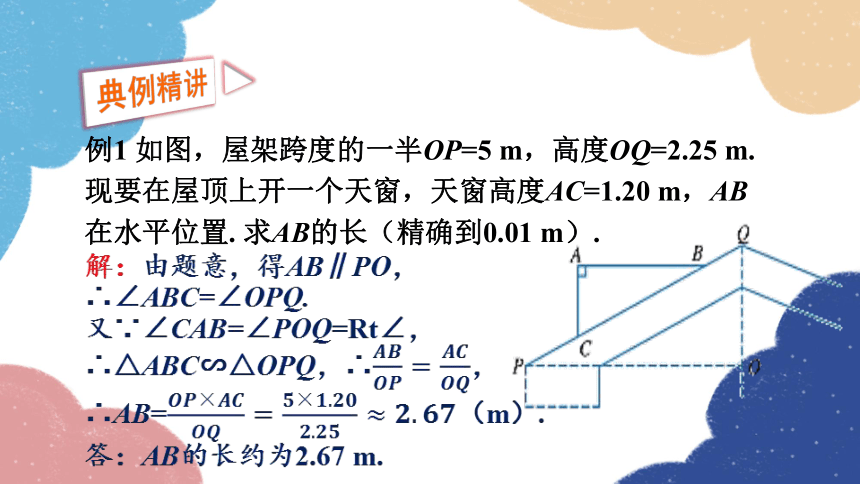
例1 如图,屋架跨度的一半OP=5 m,高度OQ=2.25 m. 现要在屋顶上开一个天窗,天窗高度AC=1.20 m,AB在水平位置. 求AB的长(精确到0.01 m).
例2 数学兴趣小组测量校园内一棵树高,有以下两种方法:
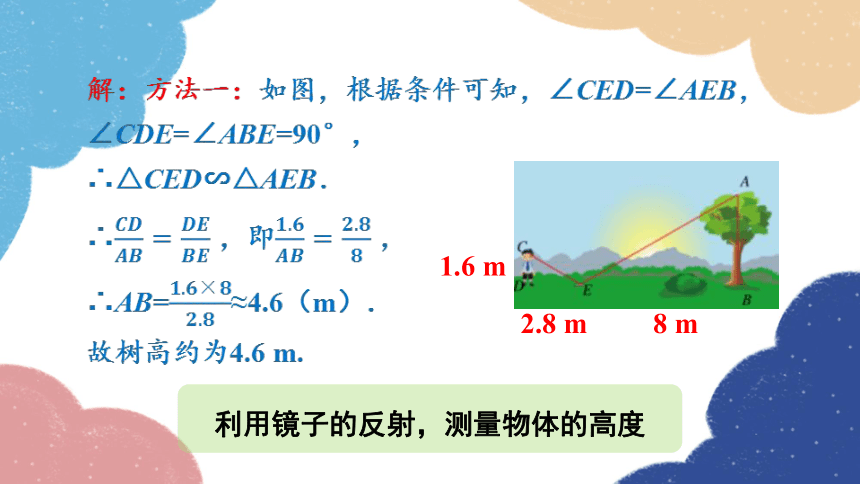
方法一:如图,把镜子放在离树(AB)8 m的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.8 m,观察者目高CD=1.6 m.
8 m
2.8 m
1.6 m
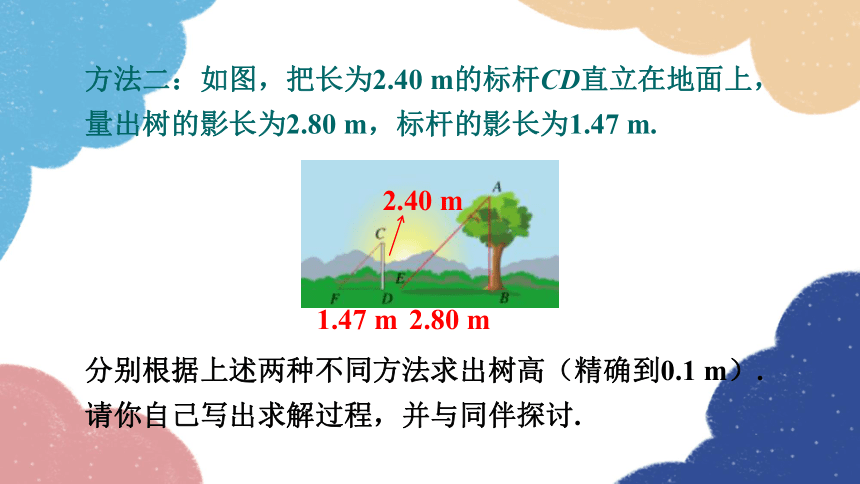
方法二:如图,把长为2.40 m的标杆CD直立在地面上,量出树的影长为2.80 m,标杆的影长为1.47 m.
分别根据上述两种不同方法求出树高(精确到0.1 m).
请你自己写出求解过程,并与同伴探讨.
1.47 m
2.80 m
2.40 m
8 m
2.8 m
1.6 m
利用镜子的反射,测量物体的高度
1.47 m
2.80 m
2.40 m
还有其他测量树
高的方法吗?
利用阳光下的影子,测量物体的高度
A
B
H
G
E
F
D
C
方法三:如图所示,在地面上直立一根标杆EF,沿着直线BF后退到点D. 使眼睛C、标杆的顶端E、树梢顶点A在同一直线上,量出DF,FB的长度,根据目高和标杆的高度就可以求出树的高度.
利用标杆,测量物体的高度
A
B
H
G
E
F
D
C
方法四:如图所示,用手举一根标尺EF,使标尺与地面垂直,当标尺刚好挡住树的高度时,量出眼睛到标尺的距离CG,人到树的距离CH,利用相似三角形对应高线长之比等于相似比,即可求出树的高度.
利用标尺,测量物体的高度
课下自己写出方法三、四的求解过程,并与同伴探讨.
解答相似三角形实际应用问题的基本步骤:
(1)审题:理解题意,并根据题意画出图形;
(2)建模:根据具体类型及图形构造相似三角形,即
建立相似三角形模型;
(3)解题:根据相似三角形的性质列式解决问题.
应用相似三角形的知识来解决实际问题的关键是画出示意图,将实际问题转化为数学问题,体现了数学建模思想.
课堂小结
相似三角形的应用
1.审题
2.建模
3.解题
测量物体的高度
利用镜子的反射
利用阳光下的影子
利用标杆
利用标尺
解答相似三角形实际应用问题的基本步骤
1.如图为步枪在瞄准时的示意图,从眼睛到准星的距离OE为80 cm,步枪上的准星宽度AB为2 mm,目标的正面宽度CD为50 cm,求眼睛到目标的距离OF.
当堂检测
准星
2.如图,一只箱子沿着斜面向上运动,箱高AB=1.2 m. 当BC=2.4 m时,点B离地面的距离BE=1.4 m,求此时点A离地面的距离(精确到0.1 m).
O
2.如图,一只箱子沿着斜面向上运动,箱高AB=1.2 m. 当BC=2.4 m时,点B离地面的距离BE=1.4 m,求此时点A离地面的距离(精确到0.1 m).
O
感谢观看!
4.5 相似三角形的性质及其应用
第3课时 相似三角形的应用
学习目标
进一步掌握和理解相似三角形的性质.
能运用相似三角形的有关性质解决简单的实际问题.
知识回顾
迄今为止,我们都学习了哪些相似三角形的性质?
1.相似三角形的对应角相等,对应边成比例.
2.相似三角形对应线段的比都等于相似比.
3.相似三角形的周长之比等于相似比;
相似三角形的面积之比等于相似比的平方.
下面我们来看相似三角形性质的一些实际应用.
典例精讲
例1 如图,屋架跨度的一半OP=5 m,高度OQ=2.25 m. 现要在屋顶上开一个天窗,天窗高度AC=1.20 m,AB在水平位置. 求AB的长(精确到0.01 m).
例2 数学兴趣小组测量校园内一棵树高,有以下两种方法:
方法一:如图,把镜子放在离树(AB)8 m的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.8 m,观察者目高CD=1.6 m.
8 m
2.8 m
1.6 m
方法二:如图,把长为2.40 m的标杆CD直立在地面上,量出树的影长为2.80 m,标杆的影长为1.47 m.
分别根据上述两种不同方法求出树高(精确到0.1 m).
请你自己写出求解过程,并与同伴探讨.
1.47 m
2.80 m
2.40 m
8 m
2.8 m
1.6 m
利用镜子的反射,测量物体的高度
1.47 m
2.80 m
2.40 m
还有其他测量树
高的方法吗?
利用阳光下的影子,测量物体的高度
A
B
H
G
E
F
D
C
方法三:如图所示,在地面上直立一根标杆EF,沿着直线BF后退到点D. 使眼睛C、标杆的顶端E、树梢顶点A在同一直线上,量出DF,FB的长度,根据目高和标杆的高度就可以求出树的高度.
利用标杆,测量物体的高度
A
B
H
G
E
F
D
C
方法四:如图所示,用手举一根标尺EF,使标尺与地面垂直,当标尺刚好挡住树的高度时,量出眼睛到标尺的距离CG,人到树的距离CH,利用相似三角形对应高线长之比等于相似比,即可求出树的高度.
利用标尺,测量物体的高度
课下自己写出方法三、四的求解过程,并与同伴探讨.
解答相似三角形实际应用问题的基本步骤:
(1)审题:理解题意,并根据题意画出图形;
(2)建模:根据具体类型及图形构造相似三角形,即
建立相似三角形模型;
(3)解题:根据相似三角形的性质列式解决问题.
应用相似三角形的知识来解决实际问题的关键是画出示意图,将实际问题转化为数学问题,体现了数学建模思想.
课堂小结
相似三角形的应用
1.审题
2.建模
3.解题
测量物体的高度
利用镜子的反射
利用阳光下的影子
利用标杆
利用标尺
解答相似三角形实际应用问题的基本步骤
1.如图为步枪在瞄准时的示意图,从眼睛到准星的距离OE为80 cm,步枪上的准星宽度AB为2 mm,目标的正面宽度CD为50 cm,求眼睛到目标的距离OF.
当堂检测
准星
2.如图,一只箱子沿着斜面向上运动,箱高AB=1.2 m. 当BC=2.4 m时,点B离地面的距离BE=1.4 m,求此时点A离地面的距离(精确到0.1 m).
O
2.如图,一只箱子沿着斜面向上运动,箱高AB=1.2 m. 当BC=2.4 m时,点B离地面的距离BE=1.4 m,求此时点A离地面的距离(精确到0.1 m).
O
感谢观看!
同课章节目录
