二次函数

课件29张PPT。中考复习：二次函数二次函数复习要点例题讲解巩固训练归纳小结能力训练一、定义二、顶点与对称轴三、解析式的求法四、图象位置与
a、b、c、 △ 的
正负关系
一般地，如果
y=ax2+bx+c(a，b，c
是常数，a≠0)，那么，y
叫做x的二次函数。
一、定义二、顶点与对称轴三、解析式的求法四、图象位置与
a、b、c、 △ 的
正负关系一、定义二、顶点与对称轴三、解析式的求法四、图象位置与
a、b、c、 △ 的
正负关系y=ax2+bx+c 对称轴： x=– 顶点坐标：（– ， ）一、定义二、顶点与对称轴三、解析式的求法四、图象位置与
a、b、c、 △ 的
正负关系y=ax2+bx+c
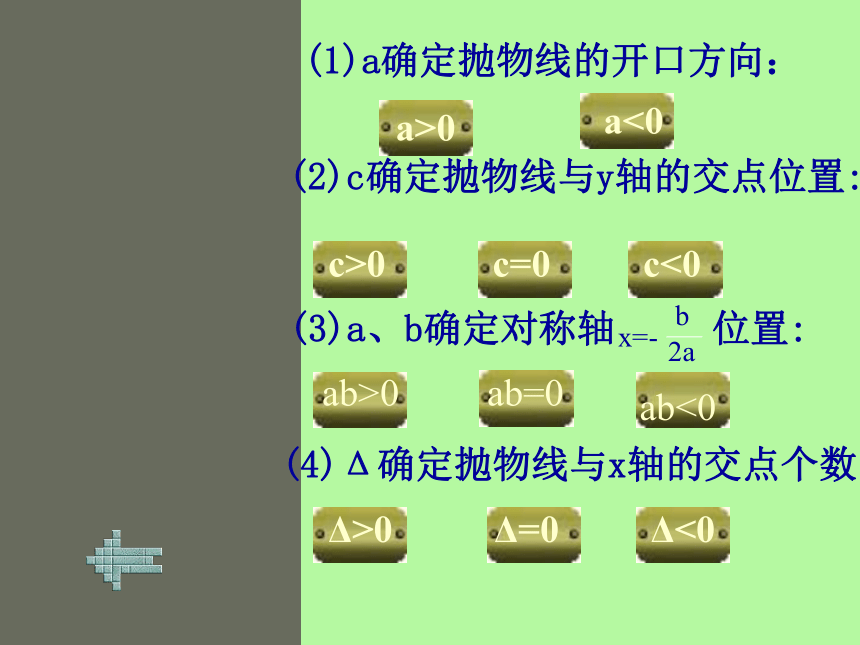
y=a(x-x1)(x-x2)　y=a(x-h)2+kc>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：a>0a<0
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：
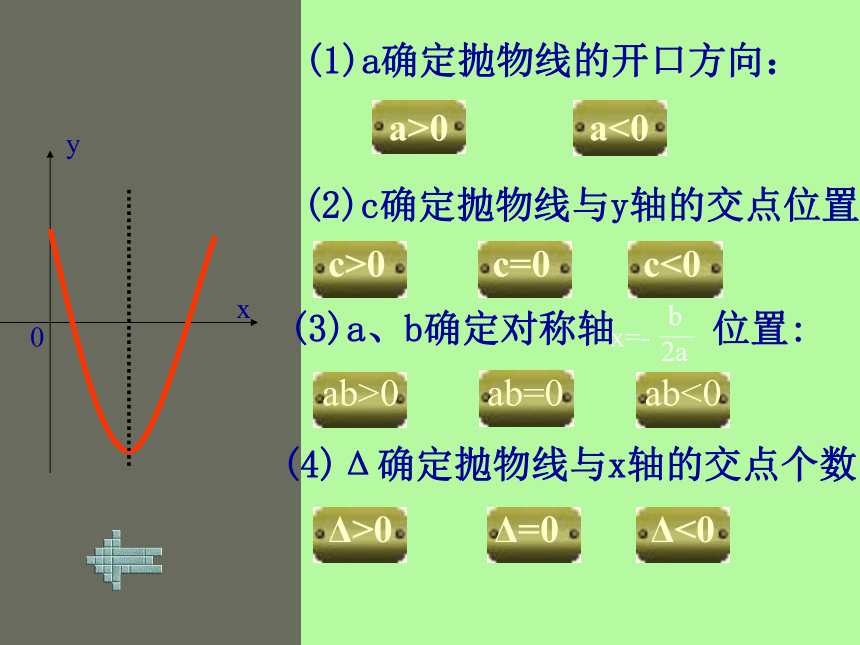
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向：y (2)c确定抛物线与y轴的交点位置: x (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向：y (2)c确定抛物线与y轴的交点位置: x (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：?(0,0)
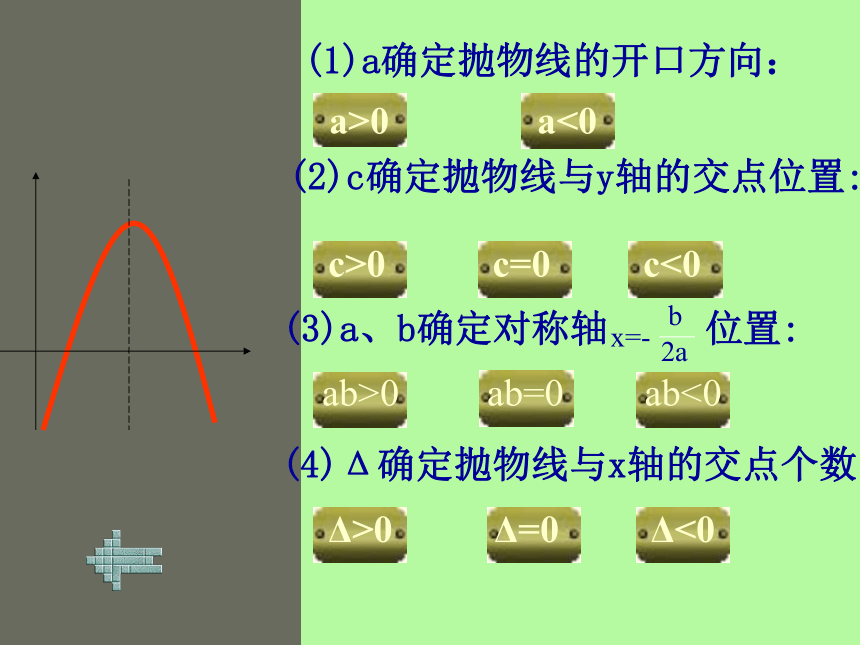
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：xy0?(0,c)
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：xy0
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：xy0
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：xy0??
a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：xy0?a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a确定抛物线的开口方向： (2)c确定抛物线与y轴的交点位置: (3)a、b确定对称轴 位置:(4)Δ确定抛物线与x轴的交点个数：xy0?例1、已知二次函数y=—x2+x- —
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
2213例1、已知二次函数y=—x2+x- —
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
1223解:（1）∵a= —>0
∴抛物线的开口向上

∵y= — (x2+2x+1)-2=—(x+1)2-2
∴对称轴x=-1，顶点坐标M（-1，-2）222111例1、已知二次函数y=—x2+x- —
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
解：(2)由x=0，得y= - -—
抛物线与y轴的交点C（0，- -—）
由y=0，得—x2+x- —=0
x1=-3 x2=1
与x轴交点A（-3，0）B（1，0）
22222211333１例1、已知二次函数y=—x2+x- —
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
解0x(3)①画对称轴2213例1、已知二次函数y=—x2+x- —
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
0?M(-1,-2)??C(0,-–)??A(-3,0)B(1,0)3 2xDy2213例1、已知二次函数y=—x2+x- —
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
解解0x??(0,-–)??(-3,0)(1,0)3 2:(5)?(-1,-2)当x=-1时，y有最小值为
y最小值=-2
当x≤-1时，y随x的增大
而减小;2213例1、已知二次函数y=—x2+x- —
（1）求抛物线开口方向，对称轴和顶点M的坐标。
（2）设抛物线与y轴交于C点，与x轴交于A、B两点，求C， A，B的坐标。
（3）画出函数图象的示意图。
（4）求ΔMAB的周长及面积。
（5）x为何值时，y随的增大而减小，x为何值时，y有最大（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
解：0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2x由图象可知返回2213巩固练习（1）二次函数y=x2-x-6的图象顶点坐标是___________对称轴是_________。
（2）抛物线y=-2x2+4x与x轴的交点坐标是___________
（3）已知函数y=—x2-x-4，当函数值y随x的增大而减小时，x的取值范围是___________
（4）二次函数y=mx2-3x+2m-m2的图象经过原点，则m= ____。
（0，0）（2，0）x<12２１归纳小结：（1）二次函数y=ax2+bx+c及抛物线的性质和应用
注意：图象的递增性，以及利用图象求自变量x或函
数值y的取值范围能力训练 二次函数的图象如图所示，则在下列各不等式
中成立的个数是____________1-10xy返回①abc<0
②a+b+c < 0
③a+c > b
④2a+b=0
⑤Δ=b-4ac > 0
３个谢谢你的参与制作人　方树刚