5.4 一元一次不等式组（2）

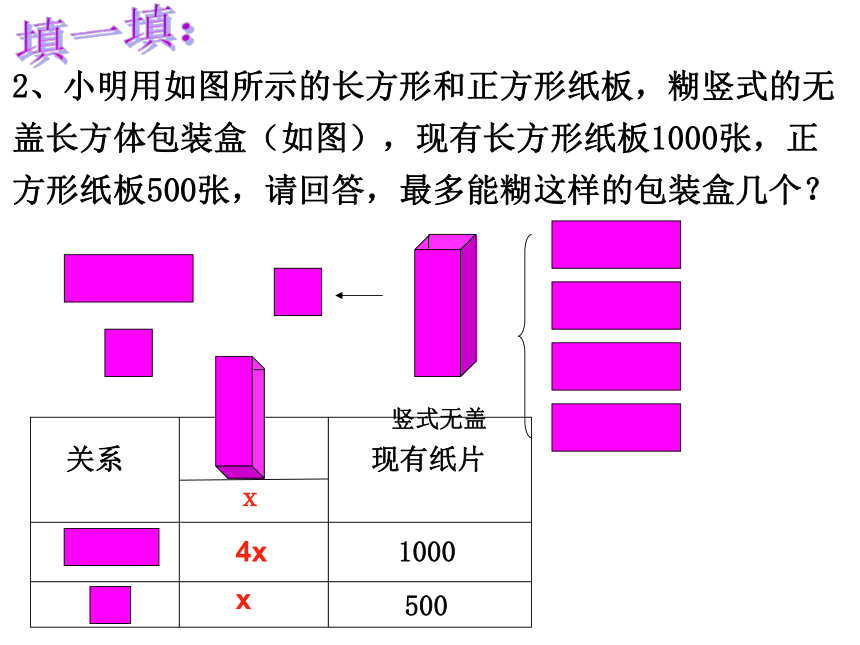
课件22张PPT。5.4一元一次不等式组(2)回顾1.一元一次不等式组　　由几个同一未知数的一元一次不等式所组成的一组不等式，叫做一元一次不等式组。2.不等式组的解　组成不等式组的各个不等式的解的公共部分就是不等式组的解。 当它们没有公共部分时，我们称这个不等式组无解。3.规律: 大大取大， 小小取小； 大小小大中间找，大大小小解不了。做一做解下列不等式（组）做一做问题情景:我们用X根火柴棒首尾相接,能围成多少种不同的等腰三角形?若X=3若X=5若X=4若X=6若X=36…0种. 边长: 不能确定一种. 边长: 1,1,1.一种. 边长: 2,2,1.一种. 边长: 2,2,2.八种. 边长: …从中看出,简单的拼拼画画就可答出;复杂的可运用不等式组的解来确定. 1、在上次的数学独立练习中,小颖考了98分,小刚考了80分,小强说:他的分数比小刚的1.2倍还要多,但没有超过小颖.如果设小强的分数为x,则根据题意可列不等式组为试一试：2、已知三个连续自然数之和小于12,求这三个数.3、把若干个苹果分给几名小朋友,如果每人分3个,余8个;如果每人分5个,最后一名小朋友能得到苹果,但不足5个,求小朋友人数和苹果的个数.0,1,2或1,2,3或2,3,45 , 23 或 6 , 26试一试：1 、小明用如图所示的长方形和正方形纸板，糊横式的无盖长方体包装盒（如图），现有长方形纸板10张，正方形纸板5张，请尝试一下，然后回答，最多能糊这样的包装盒几个？分析：3x5１０2xｘ填一填：2、小明用如图所示的长方形和正方形纸板，糊竖式的无盖长方体包装盒（如图），现有长方形纸板1000张，正方形纸板500张，请回答，最多能糊这样的包装盒几个？填一填：4x5001000关系现有纸片xｘ 例1、某工厂用如图所示的长方形和正方形纸板，糊横式与竖式两种无盖的长方体包装盒，如图。现有长方形纸板351张，正方形纸板151张，要糊的两种包装盒品的总数为100个。若按两种包装盒的生产个数分，问有几种生产方案？如果从原材料的利用率考虑，你认为应选择哪一种方案？横式无盖竖式无盖x100-x3x(张)（张）4（100-x)2x100-x 合计（张）现有纸板（张）3x+4(100-x)2x+100-x351151长方形纸板351张，正方形纸板151张，要糊的两种包装盒的总数为100个 (我们可以列表表示关系)关系　　解：设生产横式无盖的长方体包装盒x个，则生产竖式无盖的长方体包装盒（100-x）个.由题意得化简，得解这个不等式，得49≤x≤51.因为x是整数，所以x=49或x=50或x=51.解这个不等式，得49≤x≤51.因为x是整数，所以x=49或x=50或x=51.　当x＝49时，400-x＝351，100+x＝149，长方形纸板恰好用完，正方形纸板剩2张；　当x＝50时，400-x＝350，100+x＝150，长方形、正方形纸板各剩1张；　当x＝51时，400-x＝349，100+x＝151，长方形纸板剩2张，正方形纸板恰好用完。　由于长方形纸板的面积大于正方形纸板的面积，所以当x＝49时，原材料的利用率最高。　　答：一共有三种方案：(1)横式的包装盒生产49个，竖式的生产50个；（2）横式的和竖式的包装盒各生产50个；（3）横式的包装盒生产51个，竖式的包装盒生产49个。第（1）种方案原材料的利用率最高。(1)审题---明确不等关系的词语的联系与区别.
　　(如:“不超过” 、“至少”等词语的含义）运用不等式(组)解应用题一般步骤:(5)解答---利用不等式(组)的解,写出符合题意的结果.(4)解不等式(组)---根据不等式的性质.(3)列不等式(组)---选与未知数相关的不等关系.(2)设元---选合适的量为未知数. 在上题的方案（1）中横式的包装盒生产49个，竖式的生产51个，其中需要长方形纸板351张，正方形纸板149张。
如果甲工人专门生产长方形纸板，每天可做30张；乙工人专门生产正方形纸板，每天可做20张，那么，至少需要几天才能按方案（1）生产出所需的包装盒的数量。解：设至少需要y天才能按方案（1）生产出所需的包装盒的数量，由题意，得解得： y≥ 11.7 因为y是整数,所以y最小取12.答:至少需要12天才能按方案（1）生产出所需的包装盒的数量。由① 式得，y ≥ 11.7
由② 式得, y ≥7.45想一想例2、八年(9)班共有50名学生，老师安排每人制作一件A型或B型的陶艺品。学校现有甲种制作材料36千克，乙种制作材料29千克，制作A、B两种型号的陶艺品的用料情况如下表：(1)设制作B型陶艺品x件,求x的取值范围解得18≤x≤20(2)请根据学校现有材料,分别写出制作的方案.∵x是正整数 ∴x=18,19,20.1、某校师生春游,如果单独租用45座客车若干辆,刚好坐满;如果单独租用60座客车可少租1辆,且有30个空座位.(1)求该校参加春游的人数.解:设45座客车x辆
则45x=60(x-1)-30
解之,得 x=6
∴ 45x=270.还有其它做法吗?设参加春游的人数为x人
则
解得 x=270练一练：(2)已知45座的客车的租金为每辆250元, 60座的客车的租金为每辆300元,此次春游同时租用这两种客车,其中60座的客车比45座的客车多租1辆,且租金比单独租用一种客车要节省,按这种方案需用租金多少元?解：设45座的客车租用y辆，则：解得 ∵x是整数
∴y=2此时租金为250×2+300×3=1400(元)练一练：2、建网就等于建一所学校，某中学为加强现代信息技术课教学，拟投资建一个初级计算机机房和一个高级计算机机房，每个计算机机房只配置1台教师用机，若干台学生用机。其中初级机房教师用机每台8000元，学生用机每台3500元；高级机房教师用机每台11150元，学生用机每台7000元，已知两机房购买计算机的总钱数相等，且每个机房购买计算机的总钱数不少于20万也不超过21万，则该校拟建初级计算机机房、高级计算机机房各应有多少台计算机？练一练：谈谈这节课你的收获?运用不等式(组)解应用题一般步骤:(1)审题(5)解答(4)解不等式(组）(3)列不等式(组）(2)设元拓展提高: 某自行车厂今年生产销售一种新型自行车,现向你提供以下有关信息:
(1)该厂去年已备有自行车车轮10000只,车轮车间今年平均每月可生产车轮1500只,每辆自行车需装配2只车轮;
(2)该厂装配车间(自行车最后一道工序的生产车间)每月至少可装配这种自行车1000辆,但不超过1200辆;
(3)该厂已收到各地客户今年订购这种自行车共14500辆的订单;
(4)这种自行车出厂销售单价为500元/辆.
设该厂今年这种自行车销售金额为a万元,请根据以上信息,判断a的取值范围是 .参考答案: 600≤a≤700再见！