4.3 坐标平面内图形的轴对称和平移 课件(共16张PPT)-2023-2024学年八年级数学上册同步精品课堂(浙教版)
文档属性
| 名称 | 4.3 坐标平面内图形的轴对称和平移 课件(共16张PPT)-2023-2024学年八年级数学上册同步精品课堂(浙教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 960.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
坐标平面内的轴对称和平移
浙教版 八年级上册
例题1 若点A关于x轴对称的点的坐标是(a, -2), 关于y轴对称的点的坐标是(1, b), 则点A的坐 标是( ).
A.(a, -b) B.(b, -a)
C.(-1, 2) D.(-2, 1)
题型一 利用轴对称变换中点的坐标变化规律求解
C
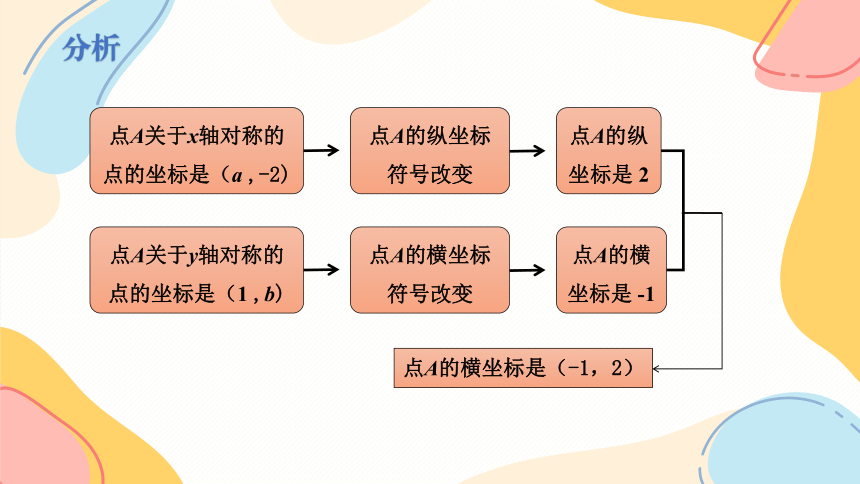
分析
点A关于x轴对称的点的坐标是(a ,-2)
点A的纵坐标符号改变
点A的纵坐标是 2
点A关于y轴对称的点的坐标是(1 ,b)
点A的横坐标符号改变
点A的横坐标是 -1
点A的横坐标是(-1,2)
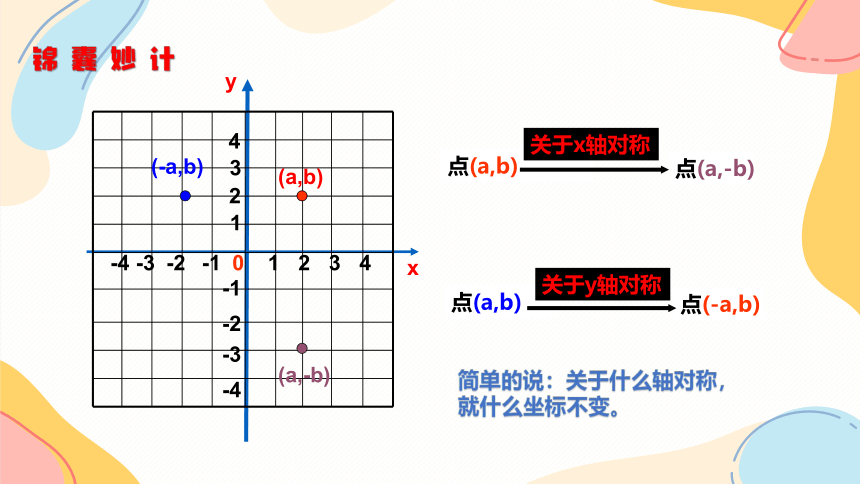
锦囊妙计
1
(a,b)
x
y
点(a,b)
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
0
(-a,b)
(a,-b)
点(a,-b)
点(a,b)
点(-a,b)
简单的说:关于什么轴对称,就什么坐标不变。
关于x轴对称
关于y轴对称
题型二 利用平移中点的坐标变化规律求解
例题2 在平面直角坐标系中, 线段AB的两个端点的坐标分别为A(-1, -1), B(1, 2), 平移线段AB, 得到线段A′B′, 若A′的坐标为(3, -1), 则点B′的坐标 为( ).
A.(4, 2) B.(5, 2)
C.(6, 2) D.(5, 3)
B
分析 点A(-1, -1)平移后得到点A′(3, -1) 向右平移4个单位长度 点B(1, 2)的对应点的坐标为 (1+4, 2), 即为(5, 2).
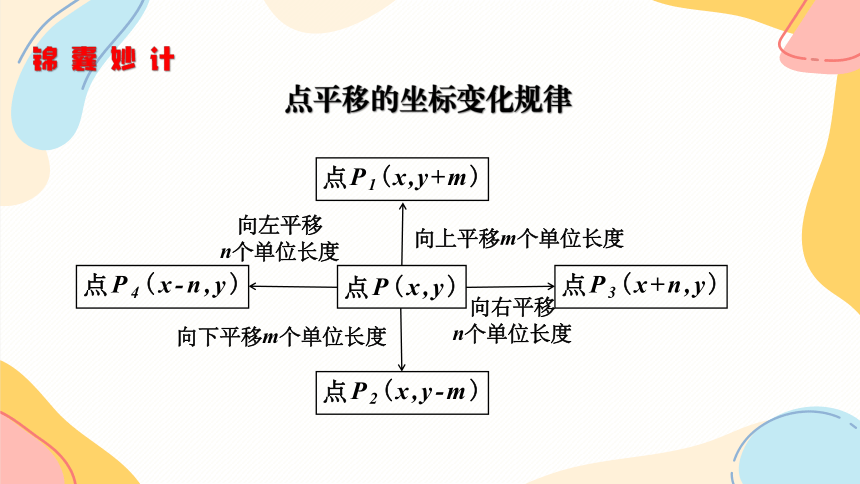
锦囊妙计
点平移的坐标变化规律
点P(x,y)
向上平移m个单位长度
向右平移
n个单位长度
向下平移m个单位长度
向左平移
n个单位长度
点P1(x,y+m)
点P2(x,y-m)
点P3(x+n,y)
点P4(x-n,y)
题型三 利用两点的位置关系确定未知字母的值
例题3 若A( a+2, 4-b ), B( 2b+3, 2a )是关于 x 轴对称的两点, 则ab的值为______.
6
分析
A( a+2, 4-b )
B( 2b+3, 2a )
a+2 = 2b+3 , 4-b= -2a
关于x轴对称:横坐标不变,纵坐标互为相反数
a= -3
b= -2
题型四 应用轴对称或平移知识进行图形变换
例题4 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),
C(5,2).
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
(2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标.
B
●
●
●
C
A
做一个图形关于坐标轴的轴对称图形,怎样画最简便呢?
1、作出三角形三个顶点关于坐标轴的对称点。
2、连接三个对称点,所得图形即为所求对称图形.
o
x
y
(2,4)
(1,2)
(5,2)
B
●
●
●
C
A
●
A1(-2,4)
●
B1(-1,2)
●
B2(1,-2)
●
C2(5,-2)
●
A2(-2,4)
o
x
y
(2,4)
(1,2)
(5,2)
●
C1(-5,2)
1、作出三角形三个顶点关于坐标轴的对称点。
2、连接三个对称点,所得图形即为所求对称图形.
锦囊妙计
解决多次图形变换问题常用方法
若图形进行了多次变换, 一般先写出第一次变换后各对应点的坐标, 再写出第二次变换后各对应点的坐标……直至得到最后一次变换后各对应点的坐标, 最后描点画图.
如图,已知网格上最小的正方形的边长为1.
(1)分别写出A、B、C三点的坐标
(2)作△ABC关于y轴对称的图形△A′B′C′(不写作法)并回答关于y轴对称的两个点之间有什么关系?
解:(1)A(-3,3),B(-5,1),C(-1,0)
(2)如图所示:
关于y轴对称的两个点的连线段被y轴垂直平分.
1.将图中三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后的三个顶点的坐标是( )
A.(2,2),(3,4),(1,7)
B.(﹣2,2),(4,3),(1,7)
C.(﹣2,2),(3,4),(1,7)
D.(2,﹣2),(3,3),(1,7)
解:由题意可知此题平移规律是:(x+2,y+3),
照此规律计算可知原三个顶点(-1,4),(-4,-1),(1,1)平移后三个顶点的坐标是(1,7),(-2,2),(3,4).
C
举一反三
2.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
A.0 B.-1 C.1 D.(-3)2009
解:∵点P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,
∴a=3,b=-4,
∴(a+b)2009=(3-4)2009=-1.
B
举一反三
3.(1)如果点A(-4,a)与点A’ (-4,-2)关于x轴对称,则
a的值为________;
(2)如果点B(-2,2b+1)与点B’(2,3)关于y轴对称,则
b的值为________;
2
1
举一反三
4.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).
将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是___________.
解:∵点A的坐标为(-1,4),
∴点C的坐标为(-3,1),
∵将△ABC沿y轴翻折到第一象限,
∴点C的对应点C′的坐标是(3,1).
故答案为:(3,1).
(3,1)
举一反三
(a,b)
向右平移h个单位
(a+h,b)
(a,b)
向左平移h个单位
(a-h,b)
(2)上下平移时:
(a,b)
向上平移h个单位
(a,b+h)
向下平移h个单位
(a,b-h )
(a,b)
(1)左右平移时:
平面直角坐标系中点平移坐标的变换:
A(a,b) 关于x轴 A1(a,-b)
A(a,b) 关于y轴 A2(-a,b)
(3)对称变换时:
坐标平面内的轴对称和平移
浙教版 八年级上册
例题1 若点A关于x轴对称的点的坐标是(a, -2), 关于y轴对称的点的坐标是(1, b), 则点A的坐 标是( ).
A.(a, -b) B.(b, -a)
C.(-1, 2) D.(-2, 1)
题型一 利用轴对称变换中点的坐标变化规律求解
C
分析
点A关于x轴对称的点的坐标是(a ,-2)
点A的纵坐标符号改变
点A的纵坐标是 2
点A关于y轴对称的点的坐标是(1 ,b)
点A的横坐标符号改变
点A的横坐标是 -1
点A的横坐标是(-1,2)
锦囊妙计
1
(a,b)
x
y
点(a,b)
2
3
4
1
2
3
4
-1
-2
-3
-4
-4
-3
-2
-1
0
(-a,b)
(a,-b)
点(a,-b)
点(a,b)
点(-a,b)
简单的说:关于什么轴对称,就什么坐标不变。
关于x轴对称
关于y轴对称
题型二 利用平移中点的坐标变化规律求解
例题2 在平面直角坐标系中, 线段AB的两个端点的坐标分别为A(-1, -1), B(1, 2), 平移线段AB, 得到线段A′B′, 若A′的坐标为(3, -1), 则点B′的坐标 为( ).
A.(4, 2) B.(5, 2)
C.(6, 2) D.(5, 3)
B
分析 点A(-1, -1)平移后得到点A′(3, -1) 向右平移4个单位长度 点B(1, 2)的对应点的坐标为 (1+4, 2), 即为(5, 2).
锦囊妙计
点平移的坐标变化规律
点P(x,y)
向上平移m个单位长度
向右平移
n个单位长度
向下平移m个单位长度
向左平移
n个单位长度
点P1(x,y+m)
点P2(x,y-m)
点P3(x+n,y)
点P4(x-n,y)
题型三 利用两点的位置关系确定未知字母的值
例题3 若A( a+2, 4-b ), B( 2b+3, 2a )是关于 x 轴对称的两点, 则ab的值为______.
6
分析
A( a+2, 4-b )
B( 2b+3, 2a )
a+2 = 2b+3 , 4-b= -2a
关于x轴对称:横坐标不变,纵坐标互为相反数
a= -3
b= -2
题型四 应用轴对称或平移知识进行图形变换
例题4 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),
C(5,2).
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
(2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标.
B
●
●
●
C
A
做一个图形关于坐标轴的轴对称图形,怎样画最简便呢?
1、作出三角形三个顶点关于坐标轴的对称点。
2、连接三个对称点,所得图形即为所求对称图形.
o
x
y
(2,4)
(1,2)
(5,2)
B
●
●
●
C
A
●
A1(-2,4)
●
B1(-1,2)
●
B2(1,-2)
●
C2(5,-2)
●
A2(-2,4)
o
x
y
(2,4)
(1,2)
(5,2)
●
C1(-5,2)
1、作出三角形三个顶点关于坐标轴的对称点。
2、连接三个对称点,所得图形即为所求对称图形.
锦囊妙计
解决多次图形变换问题常用方法
若图形进行了多次变换, 一般先写出第一次变换后各对应点的坐标, 再写出第二次变换后各对应点的坐标……直至得到最后一次变换后各对应点的坐标, 最后描点画图.
如图,已知网格上最小的正方形的边长为1.
(1)分别写出A、B、C三点的坐标
(2)作△ABC关于y轴对称的图形△A′B′C′(不写作法)并回答关于y轴对称的两个点之间有什么关系?
解:(1)A(-3,3),B(-5,1),C(-1,0)
(2)如图所示:
关于y轴对称的两个点的连线段被y轴垂直平分.
1.将图中三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后的三个顶点的坐标是( )
A.(2,2),(3,4),(1,7)
B.(﹣2,2),(4,3),(1,7)
C.(﹣2,2),(3,4),(1,7)
D.(2,﹣2),(3,3),(1,7)
解:由题意可知此题平移规律是:(x+2,y+3),
照此规律计算可知原三个顶点(-1,4),(-4,-1),(1,1)平移后三个顶点的坐标是(1,7),(-2,2),(3,4).
C
举一反三
2.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
A.0 B.-1 C.1 D.(-3)2009
解:∵点P1(a-1,5)和P2(2,b-1)关于x轴对称,
∴a-1=2,b-1=-5,
∴a=3,b=-4,
∴(a+b)2009=(3-4)2009=-1.
B
举一反三
3.(1)如果点A(-4,a)与点A’ (-4,-2)关于x轴对称,则
a的值为________;
(2)如果点B(-2,2b+1)与点B’(2,3)关于y轴对称,则
b的值为________;
2
1
举一反三
4.如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).
将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是___________.
解:∵点A的坐标为(-1,4),
∴点C的坐标为(-3,1),
∵将△ABC沿y轴翻折到第一象限,
∴点C的对应点C′的坐标是(3,1).
故答案为:(3,1).
(3,1)
举一反三
(a,b)
向右平移h个单位
(a+h,b)
(a,b)
向左平移h个单位
(a-h,b)
(2)上下平移时:
(a,b)
向上平移h个单位
(a,b+h)
向下平移h个单位
(a,b-h )
(a,b)
(1)左右平移时:
平面直角坐标系中点平移坐标的变换:
A(a,b) 关于x轴 A1(a,-b)
A(a,b) 关于y轴 A2(-a,b)
(3)对称变换时:
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
