4.2 平面直角坐标系 课件(共16张PPT)-2023-2024学年八年级数学上册同步精品课堂(浙教版)
文档属性
| 名称 | 4.2 平面直角坐标系 课件(共16张PPT)-2023-2024学年八年级数学上册同步精品课堂(浙教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-07 06:05:50 | ||
图片预览



文档简介
4.2平面直角坐标系
浙教版 八年级上册
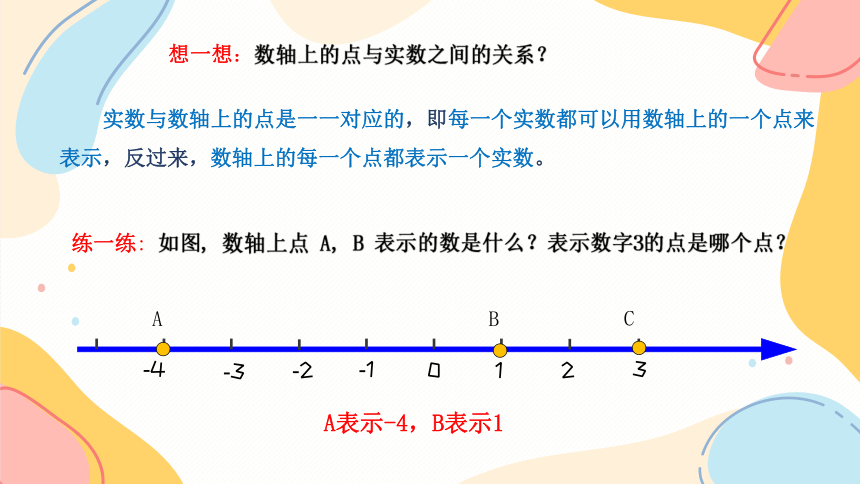
练一练: 如图, 数轴上点 A, B 表示的数是什么?表示数字3的点是哪个点?
0
2
1
3
-1
-2
-3
-4
A
B
C
想一想:数轴上的点与实数之间的关系?
实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数。
A表示-4,B表示1
·A
·C
·B
与利用数轴确定直线上点的位置类似,能不能找到一种办法来确定平面内的点的位置呢?(例如图中 A,B,C,D 各点)?
·D
O
1 2 3 4 5 6 7
7
6
5
4
3
21
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
x轴或横轴
y轴或纵轴
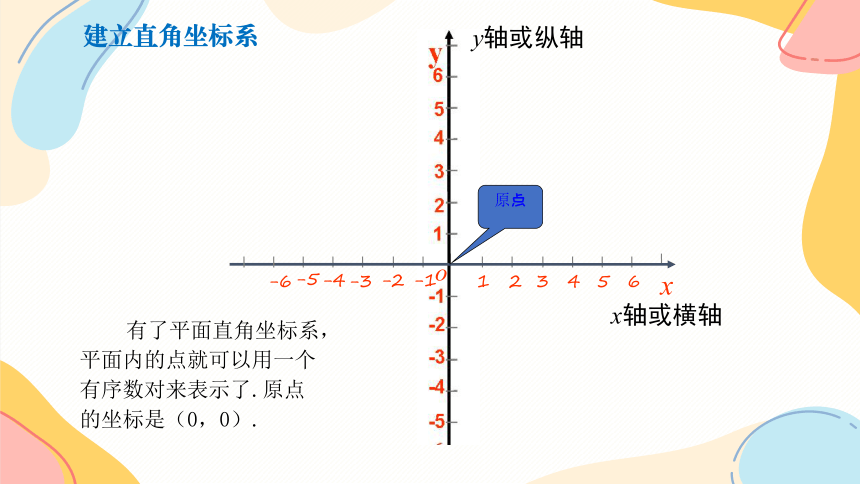
建立直角坐标系
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了.原点的坐标是(0,0).
原点
如图,建立平面直角坐标系后,坐标平面被两条坐标轴分成四部分,分别叫做第一象限,第二象限,第三象限和第四象限.坐标轴上的点不属于任何象限.
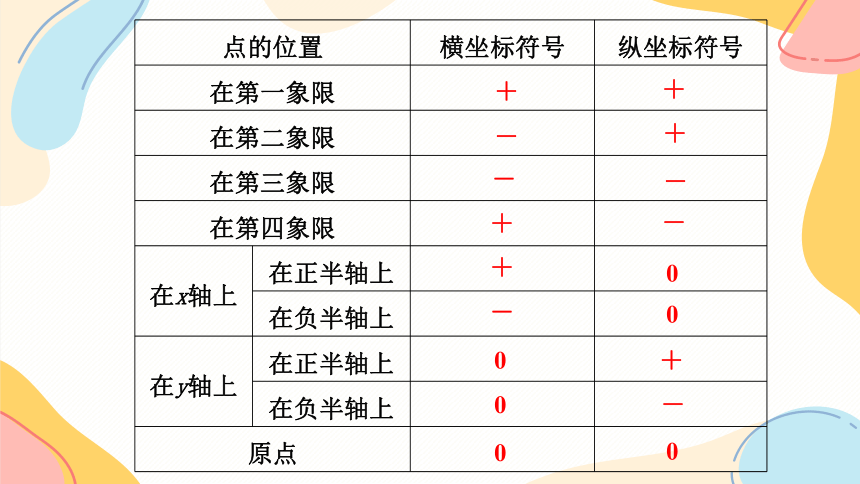
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上
在正半轴上
在负半轴上
在y轴上
在正半轴上
在负半轴上
原点
+
+
+
+
+
+
-
-
-
-
-
-
0
0
0
0
0
0
x
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
-7
7
6
y
1
2
3
4
5
-1
-2
-3
-4
-5
-6
.
A
(-3,
横坐标
纵坐标
A点在x轴上的坐标为-3
A点在y轴上的坐标为-4
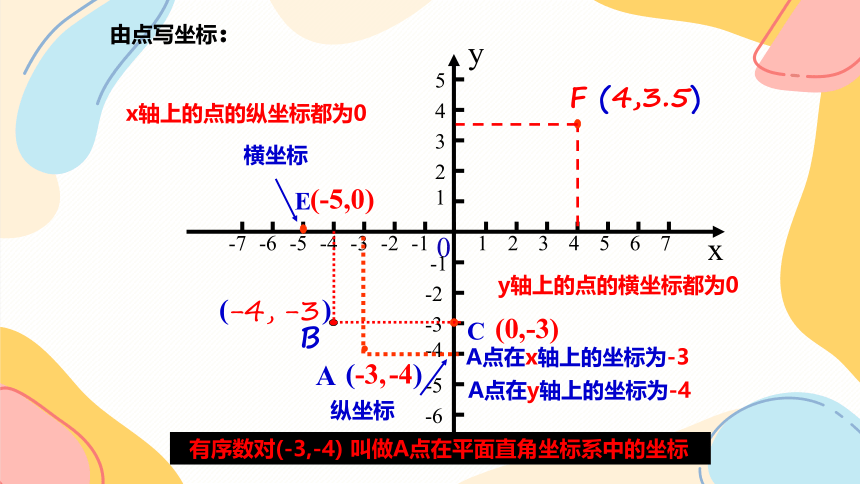
有序数对(-3,-4) 叫做A点在平面直角坐标系中的坐标
-4)
(0,-3)
C
由点写坐标:
B
E
(-5,0)
F
(4,3.5)
y轴上的点的横坐标都为0
x轴上的点的纵坐标都为0
( )
-4,
-3
4
3
2
例1(1)写出平面直角坐标系中点M、N、P、O、L的坐标.
Y
X
1
1
-1
-1
M
N
L
O
P
M(2,4)
N(-2,2)
P(2,-2.5)
O(0,0)
L(0,-2.5)
2
(2,4)
(-2,2)
(2,-2.5)
(0,0)
(0,-2.5)
-2
-3
21cnjy
(2)在平面直角坐标系中画出点 A(5,3)、B(-3,4)、 C(-4.5,0)、D(0,-4)、E(4,-3)、F(-2,????) .
?
0 1 2 3 4 5 6
6
5
4
3
2
1
x
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
O
D
C
B
F
A
E
y
x
A
B
C
D
(1)如果以点A为原点,AB所在的直线为x轴建立平面直角坐标系,那么y轴在什么位置?写出正方形的顶点A,B,C,D的坐标.
探究:如图,正方形ABCD 的边长为6.
A(0,0)
B(6,0)
C(6,6)
D(0,6)
y
(O)
x
A
B
C
D
y
O
A(-3,0)
B(3,0)
C(3,6)
D(-3,6)
(2)另建立一个平面直角坐标系,此时正方形的顶点A,B,C,D的坐标又分别是什么?
观察:平移后的坐标与原坐标有何关系?
纵坐标不变,横坐标减3
一个四边形的形状和尺寸如图所示.建立适当的坐标系,并标出各顶点的坐标.
A
B
C
D
100
200
200
150
50
0
E
1
2
A
B
C
D
0
E
1
2
解 建立直角坐标系如图,选择比例为1:10.取点E直角坐标系的原点,使四边形的边AB在 x 轴上
则可得A,B,C,D各点的坐标分别为(-1,0),(2,0),(2.5,1.5),(0,3.5).
y
x
3
1
2
3
4
-1
1.在平面直角坐标系的第二象限内有一点????,点????到????轴的距离为3,到????轴的距离为4,则点????的坐标是( )
A.(3,?4) B.(4,?3) C.(?4,3)? D.(?3,4)
?
举一反三
2.若a>0,b<-2,则点(a,b+2)应在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3. 如果????????+3,2????+4在y轴上,那么点P的坐标是( )
A.?2,0 B.0,?2 C.1,0 D.0,1
?
【详解】
解:∵????????+3,2????+4在y轴上,
∴????+3=0解得????=?3,
2????+4=2×?3+4=?2
∴点P的坐标是(0,-2).故选B.
?
举一反三
总结回顾
1.平面直角坐标系概念
2.已知点写坐标;
3.已知坐标找点.
依据
O
y
x
(+,+)
(-,+)
(-,-)
(+,-)
x轴上的点,纵坐标为0,记(x,0);
y轴上的点,横坐标为0,记(0,y).
浙教版 八年级上册
练一练: 如图, 数轴上点 A, B 表示的数是什么?表示数字3的点是哪个点?
0
2
1
3
-1
-2
-3
-4
A
B
C
想一想:数轴上的点与实数之间的关系?
实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数。
A表示-4,B表示1
·A
·C
·B
与利用数轴确定直线上点的位置类似,能不能找到一种办法来确定平面内的点的位置呢?(例如图中 A,B,C,D 各点)?
·D
O
1 2 3 4 5 6 7
7
6
5
4
3
21
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
x轴或横轴
y轴或纵轴
建立直角坐标系
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了.原点的坐标是(0,0).
原点
如图,建立平面直角坐标系后,坐标平面被两条坐标轴分成四部分,分别叫做第一象限,第二象限,第三象限和第四象限.坐标轴上的点不属于任何象限.
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上
在正半轴上
在负半轴上
在y轴上
在正半轴上
在负半轴上
原点
+
+
+
+
+
+
-
-
-
-
-
-
0
0
0
0
0
0
x
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
-7
7
6
y
1
2
3
4
5
-1
-2
-3
-4
-5
-6
.
A
(-3,
横坐标
纵坐标
A点在x轴上的坐标为-3
A点在y轴上的坐标为-4
有序数对(-3,-4) 叫做A点在平面直角坐标系中的坐标
-4)
(0,-3)
C
由点写坐标:
B
E
(-5,0)
F
(4,3.5)
y轴上的点的横坐标都为0
x轴上的点的纵坐标都为0
( )
-4,
-3
4
3
2
例1(1)写出平面直角坐标系中点M、N、P、O、L的坐标.
Y
X
1
1
-1
-1
M
N
L
O
P
M(2,4)
N(-2,2)
P(2,-2.5)
O(0,0)
L(0,-2.5)
2
(2,4)
(-2,2)
(2,-2.5)
(0,0)
(0,-2.5)
-2
-3
21cnjy
(2)在平面直角坐标系中画出点 A(5,3)、B(-3,4)、 C(-4.5,0)、D(0,-4)、E(4,-3)、F(-2,????) .
?
0 1 2 3 4 5 6
6
5
4
3
2
1
x
-6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
O
D
C
B
F
A
E
y
x
A
B
C
D
(1)如果以点A为原点,AB所在的直线为x轴建立平面直角坐标系,那么y轴在什么位置?写出正方形的顶点A,B,C,D的坐标.
探究:如图,正方形ABCD 的边长为6.
A(0,0)
B(6,0)
C(6,6)
D(0,6)
y
(O)
x
A
B
C
D
y
O
A(-3,0)
B(3,0)
C(3,6)
D(-3,6)
(2)另建立一个平面直角坐标系,此时正方形的顶点A,B,C,D的坐标又分别是什么?
观察:平移后的坐标与原坐标有何关系?
纵坐标不变,横坐标减3
一个四边形的形状和尺寸如图所示.建立适当的坐标系,并标出各顶点的坐标.
A
B
C
D
100
200
200
150
50
0
E
1
2
A
B
C
D
0
E
1
2
解 建立直角坐标系如图,选择比例为1:10.取点E直角坐标系的原点,使四边形的边AB在 x 轴上
则可得A,B,C,D各点的坐标分别为(-1,0),(2,0),(2.5,1.5),(0,3.5).
y
x
3
1
2
3
4
-1
1.在平面直角坐标系的第二象限内有一点????,点????到????轴的距离为3,到????轴的距离为4,则点????的坐标是( )
A.(3,?4) B.(4,?3) C.(?4,3)? D.(?3,4)
?
举一反三
2.若a>0,b<-2,则点(a,b+2)应在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3. 如果????????+3,2????+4在y轴上,那么点P的坐标是( )
A.?2,0 B.0,?2 C.1,0 D.0,1
?
【详解】
解:∵????????+3,2????+4在y轴上,
∴????+3=0解得????=?3,
2????+4=2×?3+4=?2
∴点P的坐标是(0,-2).故选B.
?
举一反三
总结回顾
1.平面直角坐标系概念
2.已知点写坐标;
3.已知坐标找点.
依据
O
y
x
(+,+)
(-,+)
(-,-)
(+,-)
x轴上的点,纵坐标为0,记(x,0);
y轴上的点,横坐标为0,记(0,y).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
