1.2 锐角三角函数的计算(2) 课件(共17张PPT)
文档属性
| 名称 | 1.2 锐角三角函数的计算(2) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 07:30:54 | ||
图片预览






文档简介
(共17张PPT)
浙教版九年级下册
1.2 锐角三角函数的计算(2)
第一章 解直角三角形
直角三角形的边角关系
三边的关系: 勾股定理 a2+b2=c2.
两锐角的关系:两锐角互余 ∠A+∠B=900.
边与角之间的关系:锐角三角函数
互余两角之间的三角函数关系:
sinA=cosB.
同角之间的三角函数关系:
sin2A+cos2A=1.
b
A
B
C
a
┌
c
温故知新
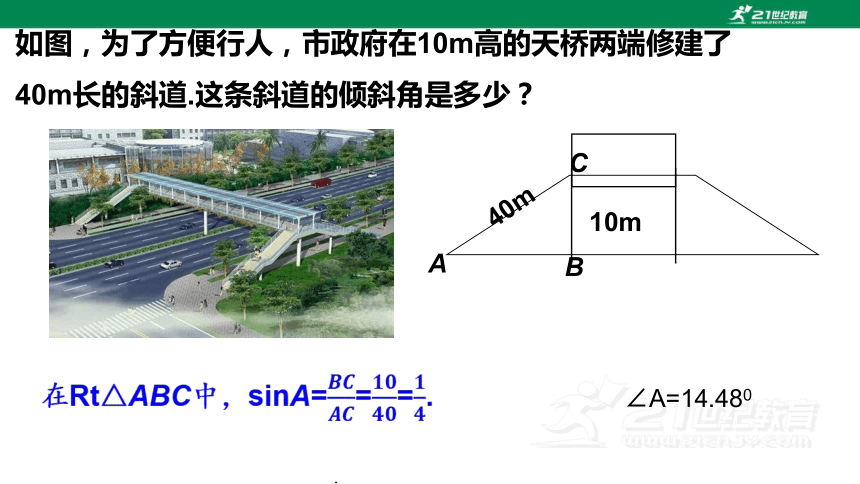
如图,为了方便行人,市政府在10m高的天桥两端修建了40m长的斜道.这条斜道的倾斜角是多少?
A
C
B
10m
40m
∠A=14.480
在Rt△ABC中,sinA===.
.
已知三角函数值求角度,要用到sin,cos,tan的第二功能健“sin-1 cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:
SHIFT
2
0
9
17.30150783
4
sin
·
7
=
如果再按“度分秒键”就换算成度分秒,
°′″
即∠ α=17018′5.43″
在生活和生产实际中经常遇到这样的问题:
已知一个角的三角函数值,要求这个角的度数,这类问题同样可以通过计算器来解决。
已知三角函数值求角度,要用到sin cos tan 键的第二功能
“sin-1,“cos-1”,“tan-1”和SHIFT键.
【例2】根据下面的条件,求锐角β的大小(精确到1”).
(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.
得 β≈26°48'51".
得 β≈38°12'52".
得 β≈54°31'55".
【例3】如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).
解:作OC⊥AB,垂足为C,则OC平分∠AOB.
在Rt△OCB中,BC= AB=100m,OB=1000m, 于是有sin∠BOC= .
∴∠BOC≈5.74°,∠AOB=5.74°×2=11.48°,
∟
C
∴弯道的长约为:l=≈200.3m
.
夯实基础,稳扎稳打
37°
53 、 37 是质数
67°
13
23 、 67 是质数
4.如图,测得一商场自动扶梯的长l为8m,该自动扶梯到达的高度h为5m. 问:自动扶梯与地面所成的角θ是多少度(精确到1 ).
解:,.
.
连续递推,豁然开朗
5.
6.
O
A
B
∟
C
AC=10cm=0.1m
sin∠AOC=
.
∠AOC≈3.80
∠AOB≈7.60
AB
l
=
≈0.2m
AB≈
AB
l
.
π≈
≈3.13
sin=
.
AB≈
AB
l
O
A
B
∟
C
AC=Rsin
.
圆内接正n边形中心角:
.
AB=2Rsin
.
π≈n×2Rsin÷2R
.
π≈nsin
.
真知在实践中诞生
7. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解: 由勾股定理
∴ A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
8.求适合下列各式的锐角α
300
450
600
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级下册
1.2 锐角三角函数的计算(2)
第一章 解直角三角形
直角三角形的边角关系
三边的关系: 勾股定理 a2+b2=c2.
两锐角的关系:两锐角互余 ∠A+∠B=900.
边与角之间的关系:锐角三角函数
互余两角之间的三角函数关系:
sinA=cosB.
同角之间的三角函数关系:
sin2A+cos2A=1.
b
A
B
C
a
┌
c
温故知新
如图,为了方便行人,市政府在10m高的天桥两端修建了40m长的斜道.这条斜道的倾斜角是多少?
A
C
B
10m
40m
∠A=14.480
在Rt△ABC中,sinA===.
.
已知三角函数值求角度,要用到sin,cos,tan的第二功能健“sin-1 cos-1,tan-1”健例如:已知sinα=0.2974,求锐角α.按健顺序为:
SHIFT
2
0
9
17.30150783
4
sin
·
7
=
如果再按“度分秒键”就换算成度分秒,
°′″
即∠ α=17018′5.43″
在生活和生产实际中经常遇到这样的问题:
已知一个角的三角函数值,要求这个角的度数,这类问题同样可以通过计算器来解决。
已知三角函数值求角度,要用到sin cos tan 键的第二功能
“sin-1,“cos-1”,“tan-1”和SHIFT键.
【例2】根据下面的条件,求锐角β的大小(精确到1”).
(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.
得 β≈26°48'51".
得 β≈38°12'52".
得 β≈54°31'55".
【例3】如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).
解:作OC⊥AB,垂足为C,则OC平分∠AOB.
在Rt△OCB中,BC= AB=100m,OB=1000m, 于是有sin∠BOC= .
∴∠BOC≈5.74°,∠AOB=5.74°×2=11.48°,
∟
C
∴弯道的长约为:l=≈200.3m
.
夯实基础,稳扎稳打
37°
53 、 37 是质数
67°
13
23 、 67 是质数
4.如图,测得一商场自动扶梯的长l为8m,该自动扶梯到达的高度h为5m. 问:自动扶梯与地面所成的角θ是多少度(精确到1 ).
解:,.
.
连续递推,豁然开朗
5.
6.
O
A
B
∟
C
AC=10cm=0.1m
sin∠AOC=
.
∠AOC≈3.80
∠AOB≈7.60
AB
l
=
≈0.2m
AB≈
AB
l
.
π≈
≈3.13
sin=
.
AB≈
AB
l
O
A
B
∟
C
AC=Rsin
.
圆内接正n边形中心角:
.
AB=2Rsin
.
π≈n×2Rsin÷2R
.
π≈nsin
.
真知在实践中诞生
7. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解: 由勾股定理
∴ A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
8.求适合下列各式的锐角α
300
450
600
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
