5.4 一元一次方程的应用(第2课时) 课件(共43张PPT)-2023-2024学年七年级数学上册同步精品课堂(浙教版)
文档属性
| 名称 | 5.4 一元一次方程的应用(第2课时) 课件(共43张PPT)-2023-2024学年七年级数学上册同步精品课堂(浙教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 00:00:00 | ||
图片预览










文档简介
(共43张PPT)
5.4 一元一次方程的应用
第2课时 销售问题、计费问题
和税率问题
数学(浙教版)
七年级 上册
第5章 一元一次方程
学习目标
1.掌握用一元一次方程解决销售问题;
2.掌握用一元一次方程解决计费问题;
3.掌握用一元一次方程解决税率问题;
导入新课
生活中,我们经常可以在各种销售场合看见一些商品优惠信息,你知道它们的意思吗?
讲授新课
知识点一 销售问题
3. 某商品原来每件零售价是 a 元,现在每件降价10%,降价后每件零售价是 元.
4. 某种品牌的彩电降价20%以后,每台售价为a元,则该品牌彩电每台原价应为 元.
1. 商品原价200元,九折出售,售价是 元.
5. 某商品按定价的八折出售,售价是12.8元,则原定售价是 元.
2. 商品进价是150元,售价是180元,则利润是 元,利润率是_____.
180
30
20%
0.9a
1.25a
16
讲授新课
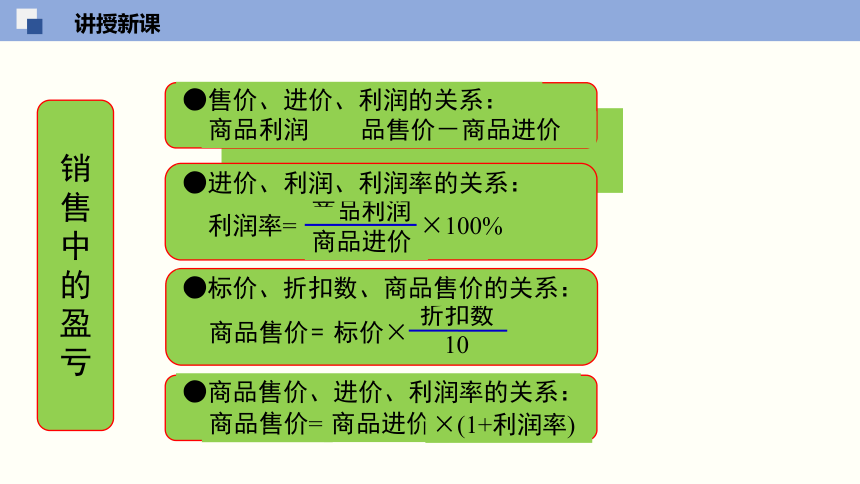
= 商品售价-商品进价
●售价、进价、利润的关系:
商品利润
商品利润
利润率=
●进价、利润、利润率的关系:
商品进价
×100%
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
中
的
盈
亏
折扣数
●标价、折扣数、商品售价的关系:
商品售价=
标价×
10
讲授新课
【例1】一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
60
60
思考:销售的盈亏取决于什么?
取决于总售价与总成本(两件衣服的成本之和)的关系
总售价(120元) > 总成本
总售价(120元) < 总成本
总售价(120元) = 总成本
盈 利
亏 损
不盈不亏
讲授新课
现在两件衣服的售价为已知条件,要知道卖这两件衣服是盈利还是亏损,还需要知道什么?
两件衣服的成本(即进价).
如果设盈利的那件衣服的进价为x 元,根据进价、利润率、售价之间的关系,你能列出方程求解吗?同理,如果设另一件衣服的进价为 y 元呢?
60
60
讲授新课
(2) 设亏损25%的衣服进价是 y元,
依题意得 y-0.25y=60.
解得 y=80.
(1) 设盈利25%的衣服进价是 x 元,
依题意得 x+0.25 x=60.
解得 x=48.
解:
两件衣服总成本:x+y=48+80=128 (元).
因为120-128=-8(元)
所以卖这两件衣服共亏损了8元.
讲授新课
【例2】某琴行同时卖出两台钢琴,每台售价为960元. 其中一台盈利20%,另一台亏损20%.这次琴行是盈利还是亏损,或是不盈不亏?
(2) 设亏损20%的钢琴进价是 y元,
依题意得 y-0.2y=960.
解得 y=1200.
(1) 设盈利20%的钢琴进价是 x 元,
依题意得 x+0.2 x=960.
解得 x=800.
解:
总成本:x+y=800+1200=2000 (元).
总收入:960×2=1920(元).
因为1920-2000=-80(元)
所以卖这两台钢琴共亏损了80元.
讲授新课
练一练
1. 某文具店有两个进价不同的计算器都卖64元,其中一个盈利60%,另一个亏本20%.这次交易中的盈亏情况?
(1) 设盈利60%的计算器进价是 x 元,
依题意得 x+0.6 x=64.
解得 x=40.
解:
总成本:x+y=40+80=120 (元).
总收入:64×2=128(元).
因为128-120=8(元)
所以卖这两个计算器共盈利8元.
(2) 设亏损20%的计算器进价是 y元,
依题意得 y-0.2y=64.
解得 y=80.
讲授新课
2、某商品的零售价是900元,为适应竞争,商店按零售价打 9 折 (即原价的 90% ),并再让利 40 元销售,仍可获利 10% ,求该商品的进价.
【分析】由题目条件,易知该商品的实际售价是( 900×90%-40 ) 元. 设该商品的进价为每件 x元,根据实际售价 (不同表示法) 相等列方程求解.
解:设该商品的进价为每件 x 元,
依题意,得 900×0.9-40=10% x +x,
解得 x=700.
答:该商品的进价为700元.
讲授新课
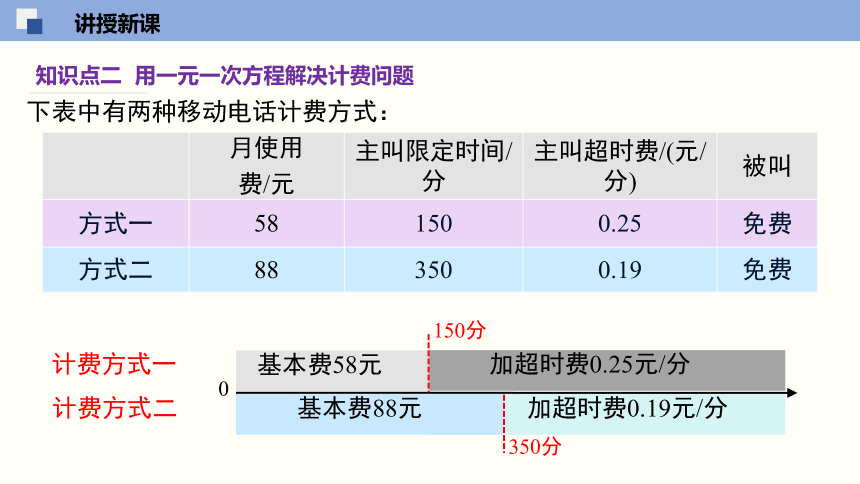
知识点二 用一元一次方程解决计费问题
下表中有两种移动电话计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
讲授新课
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
想一想 你觉得哪种计费方式更省钱?
填填下面的表格,你有什么发现?
主叫时间(分) 100 150 250 300 350 450
方式一计费(元)
方式二计费(元)
58
58
83
95.5
108
133
88
88
88
88
88
107
哪种计费方式更省钱与“主叫时间有关”.
讲授新课
考虑 t 的取值时,两个主叫限定时间 150 min和 350 min是不同时间范围的划分点.
计费时首先要看主叫是否超过限定时间,主叫不超过限定时间,月使用费一定;
主叫超过限定时间,超时部分加收超时费.
问题1 设一个月内移动电话主叫为 t min (t是正整数),列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
讲授新课
当 t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
58+0.25(t-150)
88
88
108
58+0.25(t-150)
88+0.19(t-350)
讲授新课
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题2 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
讲授新课
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
(1) 比较下列表格的第2、3行,你能得出什么结论?
①当t ≤150时,方式一计费少(58元);
讲授新课
(2) 比较下列表格的第2、4行,你能得出什么结论?
当t 大于150且小于 350时,存在某一个值,使得两种方式计费相等.
依题意 ,得58+0.25(t-150) = 88,
解得 t =270.
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
>
<
讲授新课
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
解析:当t>350分时,方式一的计费其实就是在108元的基础上,加上超过350分部分的超时费[0.25(t-350)].
(3) 当t >350分时,两种计费方式哪种更合算呢?
当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350),
方式二: 88+0.19(t-350),
所以,当t >350分时,方式二计费少.
讲授新课
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
270
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱;
时,方式一、方式二均可.
t 小于 270
t 大于 270
t 等于 270
讲授新课
列表分析
借助数轴
审题
分类讨论
更优惠
费用相同
列方程
用未知数表示费用
设未知数
如何比较两个代数式的大小
要找不等关系先找等量关系
解决“电话计费问题”的一般思路:
讲授新课
练一练
1、小明和小强为了买同一种火车模型,决定从春节开始攒钱,小明原有200元,以后每月存50元;小强原有150元,以后每月存60元.设两人攒钱的月数为x(个)(x为整数).
(1)根据题意,填写下表:
攒钱的月数/个 3 6 … x
小明攒钱的总数/元 …
小强攒钱的总数/元 …
330
500
200+50x
150+60x
350
510
讲授新课
(2)在几个月后小明与小强攒钱的总数相同?此时他们各有多少钱?
(2) 根据题意,得200+50x=150+60x,
解得x=5.
所以150+60x=450.
答:在5个月后小明与小强攒钱的总数相同,此时每人有450元钱.
讲授新课
(3)若这种火车模型的价格为780元,他们谁能够先买到该模型?
(3) 根据题意,由200+50x=780,解得x=11.6,故小明在12个月后攒钱的总数超过780元.
由150+60x=780,解得x=10.5,
故小强在11个月后攒钱的总数超过780元.
所以小强能够先买到该模型.
【点睛】解决此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
讲授新课
知识点三 用一元一次方程解决税率问题
银行中都蕴含着那些数学问题呢?
讲授新课
本金
利息
年利率
税率
实得本利和
存期
银行存款涉及哪些数量 它们有什么样的联系呢
讲授新课
1.小明把10000元钱按定期一年存入银行. 一年期定期存款的年利率为3.87%,则一年后的利息为______元.
2.利息税的税率为5%,则一年后的利息税为______元.
3.到期支取时,扣除利息税后小明实得利息为_______元.
4.到期支取时,扣除利息税后小明实得本利和为_________元.
387
19.35
367.65
10367.65
讲授新课
【例1】小明把压岁钱按定期一年存入银行,当时一年期定期存款的年利率为1.98%,利息税的税率为20%,到期支取时,扣除利息税后小明实得本利和为507.92元,问小明存入银行的压岁钱有多少元
【分析】本金多少?利息多少?利息税多少?
设哪个未知数为x?根据哪个等量关系列出方程?
讲授新课
解 :设小明存入银行的压岁钱有x元,则到期支取时,利息为1.98%x元,应缴利息税为1.98%x×20%=0.00396x元,根据题意,得
x+0.0198x-0.00396x=507.92
解这个方程,得 1.01584x=507.92
x=500
答:小明存入银行的压岁钱有500元.
讲授新课
练一练
1.老王把5000元按一年期定期储蓄存入银行.到期支取时,扣去利息税后实得本利和为5080元.已知利息税税率为20﹪,问当时一年期定期储蓄的年利率为多少?
解:设一年期定期储蓄的年利率为x,根据题意,得
解这个方程,得 x=2%
答:当时一年期定期储蓄的年利率为2%.
当堂检测
1. 某商场把进价为1980元的商品按标价的八折出售,仍获利10%,则该商品的标价为 元.
2. 我国政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品在 2015 年涨价 30% 后,2017年又降价 70% 至 a 元,则这种药品在2015 年涨价前的价格为 元.
2725
当堂检测
3. 某市为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每户每月用水不超过 7m3,则按 2 元/m3 收费;若每户每月用水超过 7 m3则超过的部分按 3元/m3 收费. 如果某居民户去年12月缴纳了 53 元水费,那么这户居民去年12月的用水量为_______m3.
20
当堂检测
4.2011年2月9日国家公布的二年期整存整取储蓄的年利率为3.90%, 免缴利息税.已知某储户存满两年后到期获得本利和为3234元, 问该储户存入本金多少元
解:设该储户存入本金x元,根据题意,得
解这个方程,得 :x=3000
答:该储户存入本金3000元.
当堂检测
解:设参加书画社的有x人,那么参加文学社的有(x+5)人.根据题意,得
解这个方程,得 :x=30.
答:参加书画社的有30人.
5、七年级二班有45人报名参加了文学社或书画社,已知参加文学社的人数比参加书画社的人数多5人,两个社都参加的有20人,问参加书画社的有多少人?
当堂检测
6. 某商品的进价是1000元,售价是1500元,由于销售情况不好,商店决定降价出售,但又要保证利润率不低于5%,那么商店最多可打几折出售此商品?
解:设商店最多可以打x折出售此商品,根据题意,得
解得 x = 7.
答:商店最多可以打7折出售此商品.
当堂检测
7. 某市生活拨号上网有两种收费方式,用户可以任选其一. A计时制:0.05 元/分钟;B包月制:60 元/月 (限一部个人住宅电话上网). 此外,两种上网
方式都得加收通信费 0.02 元/分钟.
(1) 某用户某月上网时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2) 你认为采用哪种方式比较合算?
解:(1) 采用计时制:(0.05+0.02)×60x=4.2x,
采用包月制:60+0.02×60x=60+1.2x;
当堂检测
(2) 由 4.2x = 60+1.2x,得 x=20. 又由题意可知,上
网时间越长,采用包月制越合算.所以,
当 0 < x < 20 时,采用计时制合算;
当 x=20 时,采用两种方式费用相同;
当 x > 20 时,采用包月制合算.
当堂检测
8. 用A4纸在某复印社复印文件,复印页数不超过20时每页收费0.12元;复印页数超过20时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,
不论复印多少页,每页收费0.1元. 问:如何根据复印的页数选择复印的地点使总价格比较便宜? (复印的页数不为零)
复印页数x 复印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:设复印页数为x,依题意,列表得:
(1) 当 x <20 时,0.12x 大于 0.1x 恒成立,图书馆价格便宜;
(2) 当 x = 20 时,图书馆价格便宜;
当堂检测
(3) 当 x 大于20时,依题意得
2.4+0.09(x-20) = 0.1x.
解得 x = 60
所以,当x大于20且小于60时,图书馆价格便宜;
当x等于60时,两者价格相同;
当x大于60时,复印社价格便宜.
综上所述:当 x 小于60页时,图书馆价格便宜;
当 x 等于60时,两者价格相同;
当 x 大于60时,复印社价格便宜.
课堂小结
= 商品售价-商品进价
●售价、进价、利润的关系:
商品利润
商品利润
利润率=
●进价、利润、利润率的关系:
商品进价
×100%
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
中
的
盈
亏
折扣数
●标价、折扣数、商品售价的关系:
商品售价=
标价×
10
课堂小结
列表分析
借助数轴
审题
分类讨论
更优惠
费用相同
列方程
用未知数表示费用
设未知数
如何比较两个代数式的大小
要找不等关系先找等量关系
解决“电话计费问题”的一般思路:
课堂小结
利率问题的基本数量关系:
本金×利率× 存期=利息
利息×税率=利息税
本金+利息-利息税=实得本利和
谢 谢~
5.4 一元一次方程的应用
第2课时 销售问题、计费问题
和税率问题
数学(浙教版)
七年级 上册
第5章 一元一次方程
学习目标
1.掌握用一元一次方程解决销售问题;
2.掌握用一元一次方程解决计费问题;
3.掌握用一元一次方程解决税率问题;
导入新课
生活中,我们经常可以在各种销售场合看见一些商品优惠信息,你知道它们的意思吗?
讲授新课
知识点一 销售问题
3. 某商品原来每件零售价是 a 元,现在每件降价10%,降价后每件零售价是 元.
4. 某种品牌的彩电降价20%以后,每台售价为a元,则该品牌彩电每台原价应为 元.
1. 商品原价200元,九折出售,售价是 元.
5. 某商品按定价的八折出售,售价是12.8元,则原定售价是 元.
2. 商品进价是150元,售价是180元,则利润是 元,利润率是_____.
180
30
20%
0.9a
1.25a
16
讲授新课
= 商品售价-商品进价
●售价、进价、利润的关系:
商品利润
商品利润
利润率=
●进价、利润、利润率的关系:
商品进价
×100%
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
中
的
盈
亏
折扣数
●标价、折扣数、商品售价的关系:
商品售价=
标价×
10
讲授新课
【例1】一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
60
60
思考:销售的盈亏取决于什么?
取决于总售价与总成本(两件衣服的成本之和)的关系
总售价(120元) > 总成本
总售价(120元) < 总成本
总售价(120元) = 总成本
盈 利
亏 损
不盈不亏
讲授新课
现在两件衣服的售价为已知条件,要知道卖这两件衣服是盈利还是亏损,还需要知道什么?
两件衣服的成本(即进价).
如果设盈利的那件衣服的进价为x 元,根据进价、利润率、售价之间的关系,你能列出方程求解吗?同理,如果设另一件衣服的进价为 y 元呢?
60
60
讲授新课
(2) 设亏损25%的衣服进价是 y元,
依题意得 y-0.25y=60.
解得 y=80.
(1) 设盈利25%的衣服进价是 x 元,
依题意得 x+0.25 x=60.
解得 x=48.
解:
两件衣服总成本:x+y=48+80=128 (元).
因为120-128=-8(元)
所以卖这两件衣服共亏损了8元.
讲授新课
【例2】某琴行同时卖出两台钢琴,每台售价为960元. 其中一台盈利20%,另一台亏损20%.这次琴行是盈利还是亏损,或是不盈不亏?
(2) 设亏损20%的钢琴进价是 y元,
依题意得 y-0.2y=960.
解得 y=1200.
(1) 设盈利20%的钢琴进价是 x 元,
依题意得 x+0.2 x=960.
解得 x=800.
解:
总成本:x+y=800+1200=2000 (元).
总收入:960×2=1920(元).
因为1920-2000=-80(元)
所以卖这两台钢琴共亏损了80元.
讲授新课
练一练
1. 某文具店有两个进价不同的计算器都卖64元,其中一个盈利60%,另一个亏本20%.这次交易中的盈亏情况?
(1) 设盈利60%的计算器进价是 x 元,
依题意得 x+0.6 x=64.
解得 x=40.
解:
总成本:x+y=40+80=120 (元).
总收入:64×2=128(元).
因为128-120=8(元)
所以卖这两个计算器共盈利8元.
(2) 设亏损20%的计算器进价是 y元,
依题意得 y-0.2y=64.
解得 y=80.
讲授新课
2、某商品的零售价是900元,为适应竞争,商店按零售价打 9 折 (即原价的 90% ),并再让利 40 元销售,仍可获利 10% ,求该商品的进价.
【分析】由题目条件,易知该商品的实际售价是( 900×90%-40 ) 元. 设该商品的进价为每件 x元,根据实际售价 (不同表示法) 相等列方程求解.
解:设该商品的进价为每件 x 元,
依题意,得 900×0.9-40=10% x +x,
解得 x=700.
答:该商品的进价为700元.
讲授新课
知识点二 用一元一次方程解决计费问题
下表中有两种移动电话计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费/(元/分)
主叫限定时间/分
月使用
费/元
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
讲授新课
计费方式一
0
加超时费0.19元/分
基本费88元
基本费58元
加超时费0.25元/分
150分
350分
计费方式二
想一想 你觉得哪种计费方式更省钱?
填填下面的表格,你有什么发现?
主叫时间(分) 100 150 250 300 350 450
方式一计费(元)
方式二计费(元)
58
58
83
95.5
108
133
88
88
88
88
88
107
哪种计费方式更省钱与“主叫时间有关”.
讲授新课
考虑 t 的取值时,两个主叫限定时间 150 min和 350 min是不同时间范围的划分点.
计费时首先要看主叫是否超过限定时间,主叫不超过限定时间,月使用费一定;
主叫超过限定时间,超时部分加收超时费.
问题1 设一个月内移动电话主叫为 t min (t是正整数),列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
讲授新课
当 t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
58
88
58
88
58+0.25(t-150)
88
88
108
58+0.25(t-150)
88+0.19(t-350)
讲授新课
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题2 观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
讲授新课
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
(1) 比较下列表格的第2、3行,你能得出什么结论?
①当t ≤150时,方式一计费少(58元);
讲授新课
(2) 比较下列表格的第2、4行,你能得出什么结论?
当t 大于150且小于 350时,存在某一个值,使得两种方式计费相等.
依题意 ,得58+0.25(t-150) = 88,
解得 t =270.
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
>
<
讲授新课
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于350 58+0.25(t-150) 88+0.19(t-350)
解析:当t>350分时,方式一的计费其实就是在108元的基础上,加上超过350分部分的超时费[0.25(t-350)].
(3) 当t >350分时,两种计费方式哪种更合算呢?
当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350),
方式二: 88+0.19(t-350),
所以,当t >350分时,方式二计费少.
讲授新课
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
270
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱;
时,方式一、方式二均可.
t 小于 270
t 大于 270
t 等于 270
讲授新课
列表分析
借助数轴
审题
分类讨论
更优惠
费用相同
列方程
用未知数表示费用
设未知数
如何比较两个代数式的大小
要找不等关系先找等量关系
解决“电话计费问题”的一般思路:
讲授新课
练一练
1、小明和小强为了买同一种火车模型,决定从春节开始攒钱,小明原有200元,以后每月存50元;小强原有150元,以后每月存60元.设两人攒钱的月数为x(个)(x为整数).
(1)根据题意,填写下表:
攒钱的月数/个 3 6 … x
小明攒钱的总数/元 …
小强攒钱的总数/元 …
330
500
200+50x
150+60x
350
510
讲授新课
(2)在几个月后小明与小强攒钱的总数相同?此时他们各有多少钱?
(2) 根据题意,得200+50x=150+60x,
解得x=5.
所以150+60x=450.
答:在5个月后小明与小强攒钱的总数相同,此时每人有450元钱.
讲授新课
(3)若这种火车模型的价格为780元,他们谁能够先买到该模型?
(3) 根据题意,由200+50x=780,解得x=11.6,故小明在12个月后攒钱的总数超过780元.
由150+60x=780,解得x=10.5,
故小强在11个月后攒钱的总数超过780元.
所以小强能够先买到该模型.
【点睛】解决此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
讲授新课
知识点三 用一元一次方程解决税率问题
银行中都蕴含着那些数学问题呢?
讲授新课
本金
利息
年利率
税率
实得本利和
存期
银行存款涉及哪些数量 它们有什么样的联系呢
讲授新课
1.小明把10000元钱按定期一年存入银行. 一年期定期存款的年利率为3.87%,则一年后的利息为______元.
2.利息税的税率为5%,则一年后的利息税为______元.
3.到期支取时,扣除利息税后小明实得利息为_______元.
4.到期支取时,扣除利息税后小明实得本利和为_________元.
387
19.35
367.65
10367.65
讲授新课
【例1】小明把压岁钱按定期一年存入银行,当时一年期定期存款的年利率为1.98%,利息税的税率为20%,到期支取时,扣除利息税后小明实得本利和为507.92元,问小明存入银行的压岁钱有多少元
【分析】本金多少?利息多少?利息税多少?
设哪个未知数为x?根据哪个等量关系列出方程?
讲授新课
解 :设小明存入银行的压岁钱有x元,则到期支取时,利息为1.98%x元,应缴利息税为1.98%x×20%=0.00396x元,根据题意,得
x+0.0198x-0.00396x=507.92
解这个方程,得 1.01584x=507.92
x=500
答:小明存入银行的压岁钱有500元.
讲授新课
练一练
1.老王把5000元按一年期定期储蓄存入银行.到期支取时,扣去利息税后实得本利和为5080元.已知利息税税率为20﹪,问当时一年期定期储蓄的年利率为多少?
解:设一年期定期储蓄的年利率为x,根据题意,得
解这个方程,得 x=2%
答:当时一年期定期储蓄的年利率为2%.
当堂检测
1. 某商场把进价为1980元的商品按标价的八折出售,仍获利10%,则该商品的标价为 元.
2. 我国政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品在 2015 年涨价 30% 后,2017年又降价 70% 至 a 元,则这种药品在2015 年涨价前的价格为 元.
2725
当堂检测
3. 某市为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每户每月用水不超过 7m3,则按 2 元/m3 收费;若每户每月用水超过 7 m3则超过的部分按 3元/m3 收费. 如果某居民户去年12月缴纳了 53 元水费,那么这户居民去年12月的用水量为_______m3.
20
当堂检测
4.2011年2月9日国家公布的二年期整存整取储蓄的年利率为3.90%, 免缴利息税.已知某储户存满两年后到期获得本利和为3234元, 问该储户存入本金多少元
解:设该储户存入本金x元,根据题意,得
解这个方程,得 :x=3000
答:该储户存入本金3000元.
当堂检测
解:设参加书画社的有x人,那么参加文学社的有(x+5)人.根据题意,得
解这个方程,得 :x=30.
答:参加书画社的有30人.
5、七年级二班有45人报名参加了文学社或书画社,已知参加文学社的人数比参加书画社的人数多5人,两个社都参加的有20人,问参加书画社的有多少人?
当堂检测
6. 某商品的进价是1000元,售价是1500元,由于销售情况不好,商店决定降价出售,但又要保证利润率不低于5%,那么商店最多可打几折出售此商品?
解:设商店最多可以打x折出售此商品,根据题意,得
解得 x = 7.
答:商店最多可以打7折出售此商品.
当堂检测
7. 某市生活拨号上网有两种收费方式,用户可以任选其一. A计时制:0.05 元/分钟;B包月制:60 元/月 (限一部个人住宅电话上网). 此外,两种上网
方式都得加收通信费 0.02 元/分钟.
(1) 某用户某月上网时间为x小时,请分别写出两种收费方式下该用户应该支付的费用;
(2) 你认为采用哪种方式比较合算?
解:(1) 采用计时制:(0.05+0.02)×60x=4.2x,
采用包月制:60+0.02×60x=60+1.2x;
当堂检测
(2) 由 4.2x = 60+1.2x,得 x=20. 又由题意可知,上
网时间越长,采用包月制越合算.所以,
当 0 < x < 20 时,采用计时制合算;
当 x=20 时,采用两种方式费用相同;
当 x > 20 时,采用包月制合算.
当堂检测
8. 用A4纸在某复印社复印文件,复印页数不超过20时每页收费0.12元;复印页数超过20时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,
不论复印多少页,每页收费0.1元. 问:如何根据复印的页数选择复印的地点使总价格比较便宜? (复印的页数不为零)
复印页数x 复印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:设复印页数为x,依题意,列表得:
(1) 当 x <20 时,0.12x 大于 0.1x 恒成立,图书馆价格便宜;
(2) 当 x = 20 时,图书馆价格便宜;
当堂检测
(3) 当 x 大于20时,依题意得
2.4+0.09(x-20) = 0.1x.
解得 x = 60
所以,当x大于20且小于60时,图书馆价格便宜;
当x等于60时,两者价格相同;
当x大于60时,复印社价格便宜.
综上所述:当 x 小于60页时,图书馆价格便宜;
当 x 等于60时,两者价格相同;
当 x 大于60时,复印社价格便宜.
课堂小结
= 商品售价-商品进价
●售价、进价、利润的关系:
商品利润
商品利润
利润率=
●进价、利润、利润率的关系:
商品进价
×100%
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
销
售
中
的
盈
亏
折扣数
●标价、折扣数、商品售价的关系:
商品售价=
标价×
10
课堂小结
列表分析
借助数轴
审题
分类讨论
更优惠
费用相同
列方程
用未知数表示费用
设未知数
如何比较两个代数式的大小
要找不等关系先找等量关系
解决“电话计费问题”的一般思路:
课堂小结
利率问题的基本数量关系:
本金×利率× 存期=利息
利息×税率=利息税
本金+利息-利息税=实得本利和
谢 谢~
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
