5.3 一元一次方程的解法(第1课时)(教学课件 共26张PPT)-2023-2024学年七年级数学上册同步精品课堂(浙教版)
文档属性
| 名称 | 5.3 一元一次方程的解法(第1课时)(教学课件 共26张PPT)-2023-2024学年七年级数学上册同步精品课堂(浙教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-09 20:07:30 | ||
图片预览








文档简介
(共26张PPT)
5.3 一元一次方程的解法
第1课时 移项
数学(浙教版)
七年级 上册
第5章 一元一次方程
学习目标
1.理解移项的意义,掌握移项的方法;
2.学会运用移项解形如“ax+b=cx+d”的一元一次方程;
3、能够抓住实际问题中的数量关系列一元一次方程解决实际问题;
温故知新
1.含有相同的_____,并且相同字母的_____也相同的项,叫做同类项;
2.合并同类项时,把各同类项的_____相加减,字母和字母的指数_____.
字母
指数
系数
不变
用合并同类项进行化简:
(1)3x-5x=________; (2)-3x+7x=________;
(3)y+5y-2y=________; (4) _______.
-2x
4x
4y
-y
讲授新课
知识点一 移项的定义
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本.这个班有多少学生?
解:设这个班有x名学生,
每人分4本,共分出4x本,减去缺的25本这批书共有___________本;
(4x-25)
(3x+20)
每人分3本,共分出3x本,加上剩余20本,这批书共有______________本;
列方程得_______________
3x+20=4x-25
讲授新课
问题1:把一些图书分给某班学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本.这个班有多少学生?
设这个班有x名学生,
每人分4本,共分出4x本,减去缺的25本,这批书共有___________本;
每人分3本,共分出3x本,加上剩余20本,这批书共有___________本;
列方程得__________________
3x + 20 = 4x - 25
(3x+20)
(4x-25)
这批书的总数是一个定值,表示它的两个式子英相等,
根据这一相等关系
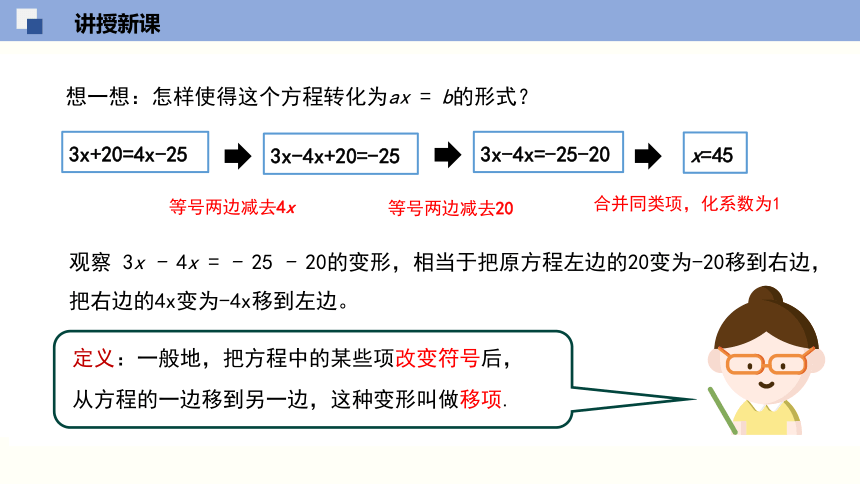
想一想:怎样使得这个方程转化为ax = b的形式?
3x+20=4x-25
等号两边减去4x
3x-4x+20=-25
等号两边减去20
3x-4x=-25-20
合并同类项,化系数为1
x=45
观察 3x - 4x = - 25 - 20的变形,相当于把原方程左边的20变为-20移到右边,
把右边的4x变为-4x移到左边。
定义:一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
讲授新课
注意:把方程转换成左边各项都含有未知数,右边各项都不含未知数的形式从而达到把方程转化为ax = b的形式,其中a,b是常数.
讲授新课
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
移项的定义
注意:移项一定要变号
移项的依据及注意事项
移项实际上是利用等式的性质1.
讲授新课
典例精析
【例1】解下列方程:
(1) 2x+5=1; (2) 8-x=3x+2.
解:(1)移项,得2x=1-5,
即 2x= -4,
两边同除以2,得 x= -2;
5 +2x =1
2x=1- 5
(2)移项,得 –x-3x =2 -8,
合并同类项,得 -4x = -6,
两边同除以 –4,得 x = .
(2)8 -x =3x +2
-x-3x=2 - 8
讲授新课
练一练
1、解方程:
(1)x+3=2x-1; (2)3x+7=32-2x .
解: (1)移项,得x-2x=-1-3,
合并同类项,得-x=-4,
两边同除以-1,得x=4;
(2)移项,得3x+2x=32-7,
合并同类项得5x=25,
系数化为1,得x=5.
讲授新课
2、下列方程中,移项正确的是 ( )
A.由x-3=4,得x=4-3
B.由2=3+x,得2-3=x
C.由3-2x=5+6,得2x-3=5+6
D.由-4x+7=5x+2,得5x-4x=7+2
B
讲授新课
把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
移项时,通常把含有未知数的项移到等号的左边,把常数项移到等号的右边.
移项的依据是什么?
移项的依据是等式的基本性质1.
移项时,应注意什么?
移项应注意:移项要变号.
讲授新课
知识点二 解决实际问题
【例2】七年级(2)班全班同学去郊游,需要一定费用,如果每位同学付5元,那么还差5.6元;如果每位同学付5.5元,那么就多出10.4元.这个班有多少名同学 总费用是多少元
讲授新课
解:设这个班有x名同学.
根据题意,得5x+5.6=5.5x-10.4.
移项,得5x-5.5x=-10.4-5.6.
合并同类项,得-0.5x=-16.
系数化为1 ,得x=32.
所以5x+5.6=165.6.答:这个班有32名同学,总费用为165.6元.
讲授新课
练一练
1.甲仓库有200t煤,乙仓库有80t煤,若甲仓库每天运出15t煤,乙仓库每天运进25t煤,则_____天后两仓库存煤量相等.
2.《九章算术》中有一个“盈不足术”的问题,其大意是:若干人共同出资买羊,每人出5钱,则差45钱;每人出7钱,则差3钱.问:人数和羊价各是多少
3
解:设人数为x.根据题意,有5x+45=7x+3.
移项,得5x-7x=3-45.
合并同类项,得-2x=-42.
系数化为1, 得x=21.所以5x+45=150.答:人数为21,羊价为150钱.
讲授新课
2.一个两位数,个位上的数是十位上的数的2倍,如果把十位上的数与个位上的数交换位置,所得的新两位数比原两位数大27,求原两位数的大小.
分析:设原两位数十位,上的数为x.
相等关系:新两位数=原两位数+27.
讲授新课
解:设原两位数十位上的数为x,则个位上的数为2x.
根据题意,得10×2x+x=10x+2x+27.
移项,得20x+x-10x-2x=27.
合并同类项,得9x=27.
系数化为1,得x=3.
所以2x=6.
答:原两位数为36.
当堂检测
1.解下列方程,并口算检验.
⑴
⑵
⑶
⑷
解:
解:
解:
解:
当堂检测
2. 通过移项将下列方程变形,正确的是 ( )
A. 由5x-7=2,得5x=2-7
B. 由6x-3=x+4,得3-6x=4+x
C. 由8-x=x-5,得-x-x=-5-8
D. 由x+9=3x-1,得3x-x=-1+9
C
当堂检测
5. 当x =_____时,式子 2x-1 的值比式子 5x+6 的值小1.
3. 已知 2m-3=3n+1,则 2m-3n =______.
4. 如果 与 互为相反数,则m的值为 .
4
-2
当堂检测
6. 小明和小刚每天早晨坚持跑步,小明每秒跑4 米,小刚每秒跑6米. 若小明站在百米起点处,小刚站在他前面10米处,两人同时同向起跑,几秒后小明追上小刚?
4x
10
6x
可得方程: 4x+10=6x.
移项,得 4x-6x=-10.
合并同类项,得 -2x=-10.
系数化为1,得 x=5.
答:小明5秒后追上小刚.
解:设小明x秒后追上小刚,
当堂检测
7. 某同学在解关于x的方程3a=2x+15时,在移项过程中2x没有改变符号,得到的方程的解为x=3.求a的值及原方程的解.
解:根据题意知,x=3是关于x的方程2x=15-3a的解,
所以2×3=15-3a,解得a=3.
把a=3代入原方程,得3×3=2x+15.
所以2x=-6,即x=-3.
所以,a的值是3,
原方程的解是x=-3.
当堂检测
8.某工厂负责生产一批零件,如果该工厂每天生产44个,就比任务量少生产20个,如果每天生产50个,则超额生产10个.求计划生产的天数.
答:计划加工5天.
解:设计划加工x天,则
44x+20 = 50x-10,
解得 x = 5.
当堂检测
9.下面是两种移动电话计费方式:
方式一 方式二
月租费 50元/月 10元/月
本地通话费 0.30元/分 0.5元/分
问:一个月内,通话时间是多少分钟时,两种移动电话计费方式的费用一样?
当堂检测
解:设通话时间t分钟,则按方式一要收费(50+0.3t)元, 按方式二要收费(10+0.4t). 如果两种移动电话计费方式的费用一样,
则 50+0.3t= 10+0.4t.
移项,得 0.3t- 0.4t =10-50.
合并同类项,得 -0.1t =-40.
系数化为1,得 t =400.
答:一个月内通话400分钟时,两种计费方式的费用一样.
课堂小结
解一元一次方程
利用合并同类项解一元一次方程
列方程解决“总量=各部分量之和”问题
转化为ax = b的形式
利用移项解一元一次方程
利用不同的式子表示同一个量来列方程解决问题
转化为ax = b的形式
谢 谢~
5.3 一元一次方程的解法
第1课时 移项
数学(浙教版)
七年级 上册
第5章 一元一次方程
学习目标
1.理解移项的意义,掌握移项的方法;
2.学会运用移项解形如“ax+b=cx+d”的一元一次方程;
3、能够抓住实际问题中的数量关系列一元一次方程解决实际问题;
温故知新
1.含有相同的_____,并且相同字母的_____也相同的项,叫做同类项;
2.合并同类项时,把各同类项的_____相加减,字母和字母的指数_____.
字母
指数
系数
不变
用合并同类项进行化简:
(1)3x-5x=________; (2)-3x+7x=________;
(3)y+5y-2y=________; (4) _______.
-2x
4x
4y
-y
讲授新课
知识点一 移项的定义
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本.这个班有多少学生?
解:设这个班有x名学生,
每人分4本,共分出4x本,减去缺的25本这批书共有___________本;
(4x-25)
(3x+20)
每人分3本,共分出3x本,加上剩余20本,这批书共有______________本;
列方程得_______________
3x+20=4x-25
讲授新课
问题1:把一些图书分给某班学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本.这个班有多少学生?
设这个班有x名学生,
每人分4本,共分出4x本,减去缺的25本,这批书共有___________本;
每人分3本,共分出3x本,加上剩余20本,这批书共有___________本;
列方程得__________________
3x + 20 = 4x - 25
(3x+20)
(4x-25)
这批书的总数是一个定值,表示它的两个式子英相等,
根据这一相等关系
想一想:怎样使得这个方程转化为ax = b的形式?
3x+20=4x-25
等号两边减去4x
3x-4x+20=-25
等号两边减去20
3x-4x=-25-20
合并同类项,化系数为1
x=45
观察 3x - 4x = - 25 - 20的变形,相当于把原方程左边的20变为-20移到右边,
把右边的4x变为-4x移到左边。
定义:一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
讲授新课
注意:把方程转换成左边各项都含有未知数,右边各项都不含未知数的形式从而达到把方程转化为ax = b的形式,其中a,b是常数.
讲授新课
一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
移项的定义
注意:移项一定要变号
移项的依据及注意事项
移项实际上是利用等式的性质1.
讲授新课
典例精析
【例1】解下列方程:
(1) 2x+5=1; (2) 8-x=3x+2.
解:(1)移项,得2x=1-5,
即 2x= -4,
两边同除以2,得 x= -2;
5 +2x =1
2x=1- 5
(2)移项,得 –x-3x =2 -8,
合并同类项,得 -4x = -6,
两边同除以 –4,得 x = .
(2)8 -x =3x +2
-x-3x=2 - 8
讲授新课
练一练
1、解方程:
(1)x+3=2x-1; (2)3x+7=32-2x .
解: (1)移项,得x-2x=-1-3,
合并同类项,得-x=-4,
两边同除以-1,得x=4;
(2)移项,得3x+2x=32-7,
合并同类项得5x=25,
系数化为1,得x=5.
讲授新课
2、下列方程中,移项正确的是 ( )
A.由x-3=4,得x=4-3
B.由2=3+x,得2-3=x
C.由3-2x=5+6,得2x-3=5+6
D.由-4x+7=5x+2,得5x-4x=7+2
B
讲授新课
把方程中的项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
移项时,通常把含有未知数的项移到等号的左边,把常数项移到等号的右边.
移项的依据是什么?
移项的依据是等式的基本性质1.
移项时,应注意什么?
移项应注意:移项要变号.
讲授新课
知识点二 解决实际问题
【例2】七年级(2)班全班同学去郊游,需要一定费用,如果每位同学付5元,那么还差5.6元;如果每位同学付5.5元,那么就多出10.4元.这个班有多少名同学 总费用是多少元
讲授新课
解:设这个班有x名同学.
根据题意,得5x+5.6=5.5x-10.4.
移项,得5x-5.5x=-10.4-5.6.
合并同类项,得-0.5x=-16.
系数化为1 ,得x=32.
所以5x+5.6=165.6.答:这个班有32名同学,总费用为165.6元.
讲授新课
练一练
1.甲仓库有200t煤,乙仓库有80t煤,若甲仓库每天运出15t煤,乙仓库每天运进25t煤,则_____天后两仓库存煤量相等.
2.《九章算术》中有一个“盈不足术”的问题,其大意是:若干人共同出资买羊,每人出5钱,则差45钱;每人出7钱,则差3钱.问:人数和羊价各是多少
3
解:设人数为x.根据题意,有5x+45=7x+3.
移项,得5x-7x=3-45.
合并同类项,得-2x=-42.
系数化为1, 得x=21.所以5x+45=150.答:人数为21,羊价为150钱.
讲授新课
2.一个两位数,个位上的数是十位上的数的2倍,如果把十位上的数与个位上的数交换位置,所得的新两位数比原两位数大27,求原两位数的大小.
分析:设原两位数十位,上的数为x.
相等关系:新两位数=原两位数+27.
讲授新课
解:设原两位数十位上的数为x,则个位上的数为2x.
根据题意,得10×2x+x=10x+2x+27.
移项,得20x+x-10x-2x=27.
合并同类项,得9x=27.
系数化为1,得x=3.
所以2x=6.
答:原两位数为36.
当堂检测
1.解下列方程,并口算检验.
⑴
⑵
⑶
⑷
解:
解:
解:
解:
当堂检测
2. 通过移项将下列方程变形,正确的是 ( )
A. 由5x-7=2,得5x=2-7
B. 由6x-3=x+4,得3-6x=4+x
C. 由8-x=x-5,得-x-x=-5-8
D. 由x+9=3x-1,得3x-x=-1+9
C
当堂检测
5. 当x =_____时,式子 2x-1 的值比式子 5x+6 的值小1.
3. 已知 2m-3=3n+1,则 2m-3n =______.
4. 如果 与 互为相反数,则m的值为 .
4
-2
当堂检测
6. 小明和小刚每天早晨坚持跑步,小明每秒跑4 米,小刚每秒跑6米. 若小明站在百米起点处,小刚站在他前面10米处,两人同时同向起跑,几秒后小明追上小刚?
4x
10
6x
可得方程: 4x+10=6x.
移项,得 4x-6x=-10.
合并同类项,得 -2x=-10.
系数化为1,得 x=5.
答:小明5秒后追上小刚.
解:设小明x秒后追上小刚,
当堂检测
7. 某同学在解关于x的方程3a=2x+15时,在移项过程中2x没有改变符号,得到的方程的解为x=3.求a的值及原方程的解.
解:根据题意知,x=3是关于x的方程2x=15-3a的解,
所以2×3=15-3a,解得a=3.
把a=3代入原方程,得3×3=2x+15.
所以2x=-6,即x=-3.
所以,a的值是3,
原方程的解是x=-3.
当堂检测
8.某工厂负责生产一批零件,如果该工厂每天生产44个,就比任务量少生产20个,如果每天生产50个,则超额生产10个.求计划生产的天数.
答:计划加工5天.
解:设计划加工x天,则
44x+20 = 50x-10,
解得 x = 5.
当堂检测
9.下面是两种移动电话计费方式:
方式一 方式二
月租费 50元/月 10元/月
本地通话费 0.30元/分 0.5元/分
问:一个月内,通话时间是多少分钟时,两种移动电话计费方式的费用一样?
当堂检测
解:设通话时间t分钟,则按方式一要收费(50+0.3t)元, 按方式二要收费(10+0.4t). 如果两种移动电话计费方式的费用一样,
则 50+0.3t= 10+0.4t.
移项,得 0.3t- 0.4t =10-50.
合并同类项,得 -0.1t =-40.
系数化为1,得 t =400.
答:一个月内通话400分钟时,两种计费方式的费用一样.
课堂小结
解一元一次方程
利用合并同类项解一元一次方程
列方程解决“总量=各部分量之和”问题
转化为ax = b的形式
利用移项解一元一次方程
利用不同的式子表示同一个量来列方程解决问题
转化为ax = b的形式
谢 谢~
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
