第七章 一次函数复习

课件38张PPT。www.1230.org 初中数学资源网第七章 一次函数复习数与形，相倚依，焉能分作两边飞？
数缺形时少直观，形少数时难入微，
数形结合百般好，隔裂分家万事非，
切莫忘，几何代数统一体，
永远联系、切莫分离！
——我国著名的数学家华罗庚一、知识要点： 1、一次函数的概念：函数y=_______(k、b为常数，k______)叫做一次函数。当b_____时，函数y=____(k____)叫做正比例函数。kx ＋b≠０ = ０≠０kx★理解一次函数概念应注意下面两点：
　　⑴、解析式中自变量x的次数是___次，
⑵、比例系数_____。1K≠0 2、正比例函数y=kx(k≠0)的图象是过点（____），(_____)的_________。
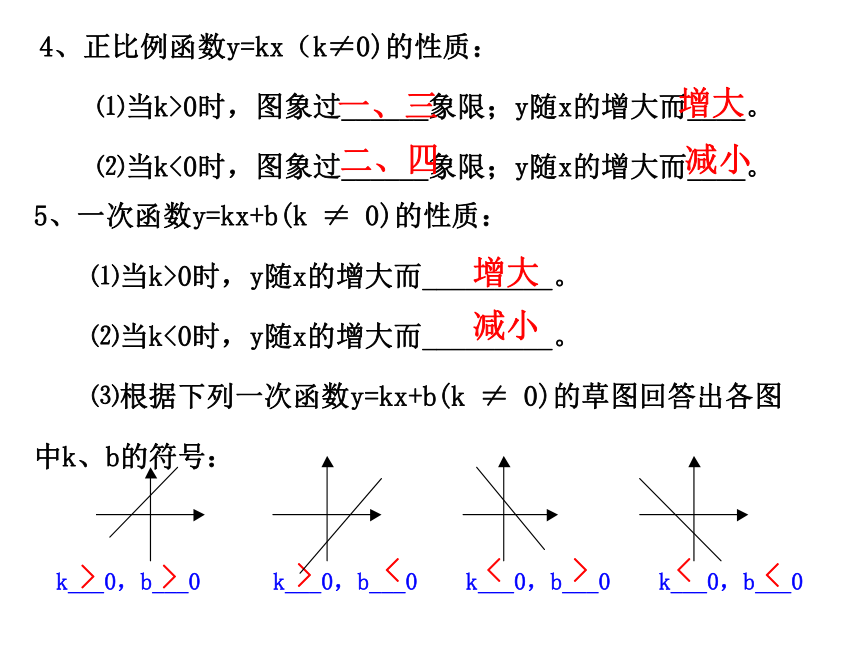
　3、一次函数y=kx+b(k≠0)的图象是过点（0，___),（____，0)的__________。0，01，k 一条直线b一条直线4、正比例函数y=kx（k≠0)的性质：
　　⑴当k>0时，图象过______象限；y随x的增大而____。
　　⑵当k<0时，图象过______象限；y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质：
　　⑴当k>0时，y随x的增大而_________。
　　⑵当k<0时，y随x的增大而_________。
　　⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号：增大减小k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0<<><<>>>解:m+1≠0,得m≠-1.m2-1=0若y是x的一次函数,则有若y是x的正比例函数,则有m+1≠0∴ m=1.故当m≠-1时, y是x的一次函数;当m=1时, y是x的正比例函数.y=kx+b
是正比例函数,
则有k≠0,b=0②①、②、③④③ (2) 如果一次函数y=kx-3k+6的图象经过原点，那么
k的值为________。
(3) 已知y-1与x成正比例，且x=－2时，y=4，那么y与
x之间的函数关系式为_________________。k=22、某函数具有下列两条性质
（1）它的图像是经过原点（0，0）的一条直线；
（2）y的值随x值的增大而增大。
请你举出一个满足上述条件的函数（用关系式表示）（-6，0）（0，4）6、若函数y＝kx+b的图像经过点（－3，－2）和（1，6）
求k、b及函数关系式。7、已知一次函数 y=（6+3m）x+n-4，求:
（1）m为何值时，y随x的增大而减小？
（2）n为何值时，函数图象与y轴交点在x轴的下方？
（3）m, n 分别为何值时，函数图象经过 (0，0).减小减小18、在直角坐标系中，一次函数y＝kx＋b的图像经过三
点A（2，0）、B（0，2）、C（m，3），求这个函数
的关系式，并求m的值。12、如果y+3与x+2成正比例，且x＝3时，y＝7
（1）写出y与x之间的函数关系式；
（2）求当x＝－1时，y的值；
（3）求当y＝0时，x的值。13、已知：y+b与x+a（a，b是常数）成正比例。
求证：y是x的一次函数。你能比较快速画出下列一次函数的图象么？
y= 2x-4, y=-x+2当x=0时y=-4，即（0，-4），
当y=0时2x-4=0，则x=2，即（0，2）画一画请画出以上两个函数的图象解：一次函数当x=1时，y=5。且它的图象与x轴交点是（６，０）。由题意得解得∴一次函数的解析式为　y= - x+6。 用待定系数法求一次函数y=kx+b的解析式，可由已知条件给出的两对x、y的值，列出关于k、b的二元一次方程组。由此求出k、b的值，就可以得到所求的一次函数的解析式。例3、已知一次函数y=kx+b(k≠0)在x=1时，y=5，且它的图象与x轴交点的横坐标是６，求这个一次函数的解析式。例4. 如图，l1反映了某公司产品的销售收入与销售量的关系，l2反映了该公司产品的销售成本与销售量的关系，根据图意填空：（1）当销售量为2吨时，销售收入＝　　　　元，销售成本＝　　　　元；20003000（2）当销售量为6吨时，销售收入＝　　　　元，销售成本＝　　　　元；60005000（3）当销售量为　　时，销售收入等于销售成本；4吨4）当销售量　　　　时，该公司赢利（收入大于成本）；
　当销售量　　　　时，该公司亏损（收入小于成本）；大于4吨小于4吨（5） l1对应的函数表达式是　　　　　　　　，
　　 l2对应的函数表达式是　　　　　　　　。y=1000xy=500x+2000做一做1、已知一次函数图象过点（1，2），求这个一次函数解析式；2、某公司营销人员的个人
收入与每月的销售业绩满足
一次函数关系，图象如图所
示，由图中的信息可知：
营销人员没有销售业绩时
的收入是______元。300×√×A温馨提示：
仔细观察图象，
捕捉有效信息！你还有什么想法？4、已知直线y= -2x+4,它与x轴的交点为A,与y轴的交点为B.
(1).求A, B两点的坐标.
(2).求?AOB的面积. (O为坐标原点)6、已知y是关于x的一次 函数，这个函数的图象经过 A（0，-8），B（1，2）两点，求当1（1）折线CAB表示某个实际问题的函数图象，请你编写一道符合该图象意义的应用题；
（2）根据你所给出的应用题分别指出x轴、y轴所表示的意义，并写出C、A、B的坐标；
（3）求图象AB的函数解析式，注明自变量x取值范围。8、由于经济和社会发展迅速，用电矛盾越来越突出，为缓
解用电紧张，电力公司制定了新的用电收费标准，每月用
电量x（度）与应付电费y（元）的关系如图所示。
⑴请你根据图像所描述的信息，分别求0≤x≤50和x>50时，
y与x函数关系式。
⑵根据你的分析：
当每月用电量不超过50度时，
收费标准是________;
当每月的用电量超过50度时，
收费标准是______________
_______________________
____________. y=0.5x (0≤x≤50) ；
y=0.9x-20 (x>50).0.5元/度 不超过50度部分按0.5元/度计算，超过部分按0.9元/度计算 　例5、柴油机在工作时油箱中的余油量Q(千克）与工作时间t（小时）成一次函数关系，当工作开始时油箱中有油40千克，工作3.5小时后，油箱中余油22.5千克
（1）写出余油量Q与时间t的函数关系式；
（2）画出这个函数的图象。解：（１）设Ｑ＝kt＋b。把t=0，Q=40；t=3.5，Q=22.5
分别代入上式，得解得解析式为：Q＝－５t+40　　(0≤t≤8)（２）取t=0，得Q=40；取t=８，得Q=０。描出点Ａ（０，40），B（8，0）。然后连成线段AB即是所求的图形。（1）求出函数关系式时，必须找出自变量的取值范围。（2）画函数图象时，应根据函数自变量的取值范围来确定图象的范围。20图象是包括
两端点的线段..AB温馨提示：1、火车站托运行李费用与托运行李的重量关系如图所示（1）当x=30时，y=_______; 当x=_______,y=30。（2）你能确定该关系所在直线的函数解析式吗？（3）当货物少于 千克，可免费托运。204010y=x+10看图回答是哪个队获胜了？ 2、10千米龙舟比赛中，红队由于某些原因，晚出发了。出发时蓝队已经划出了 500米，如图所示，?和m分别表示蓝队和红队的行驶路程y（千米）和时间x（分）之间的关系。看图回答3、某单位急需用车，准备和个体车主或租车公司签订月租车合同，设汽车每月行驶x千米，付个体车主的月费用y1元，出租公司的月租费是y2元，图象如图，观察图象回答：
1）每月行驶的路程在
什么范围内时，租公司
的车合算？
2）每月行驶的路程
等于多少时，租两家
的费用相同？
3）如果这个单位估
计每月行驶的路程为
2300千米，那么租哪
一家的车合算？4、某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后。
（1）服药后______时，血液中含药量最高，
达到每毫升_______毫克，接着逐步衰弱。
（2）服药5时，血液中含药量为每毫升____毫克。
（3）当x≤2时y与x之间的函数关系式是_____。
（4）当x≥2时y与x之间的函数关系式是____。
（5）如果每毫升血液中含药量3毫克或3毫克以上
时，治疗疾病最有效，那么这个有效时间范围是___时。.5、我国很多城市水资源缺乏，为了加强居民的节水意识，雉城镇制定了每月用水4吨以内（包括4吨）和用水4吨以上两种收费标准（收费标准：指每吨水的价格），用户每月应交水费y（元）是用水量x（吨）的函数，其函数图象如图所示。（1）观察图象，求出函数在不同范围内的解析式；并说出自来水公司在这两个用水范围内的收费标准；（2）若一用户5月份交水费12.8元，求他用了多少吨水？ 刘强的爸爸带回一张电信营业厅的资费表，上面有A、B、C三种新的手机计费标准（打电话收费，接电话不收费）（1）刘强爸爸办公室陈、秦、赵三位叔叔每月打电话约40分钟，75分钟，200分钟请算算哪种卡便宜？探究与提高（2）若有更多人需选卡，但他们打电话的时间各不相同，你能否借助一次函数图象，通过观察得出时间在什么范围内，选购哪种卡费用最省 有这样一道题目：已知，一次函数的图象y=kx+b经过点A（0,a）,B（-1，2） 则△ ABO的面积为2，请说明理由。题目中横线部分是一段被墨水污染了的无法辨认的文字。（1）根据现有信息，你能否求出题目中的一次函数的解析式？若能，请写出合适条件的一次函数解析式；（2）请根据你的理解，在横线上添加适当的条件把原题补充完整。试一试（2，0）（0，1）k=2巩固练习：2、已知y-1与x成正比例，且x=－2时，y=4，求y与x之间的函数关系式。①当k取何值时，y随x的增大而增大？
②当k取何值时，函数图象经过坐标系原点？
③当k取何值时，函数图象不经过第四象限？4、已知一次函数y＝（1－2k）x＋（2k＋1）解:① 令1-2k>0, 则k<1/2② 令2k+1=0, 则k=-1/2③ 令1-2k>0, 且2k+1>05、已知一次函数y＝(1-2m)x＋m-1，若函数y随x的增大而减小，并且函数的图象经过二、三、四象限,求m的取值范围. 7.已知一次函数的图象经过点（- 4，9）和（6，3）。
（1）求这个一次函数的关系式。
（2）试判断点（1，6）是否在这个函数的图象上。8.已知函数y=(2m+1)x+m -3
(1)若函数图象经过原点,求m的值
(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.9.已知一次函数y = kx + b的图象如图所示。
（1）求k、b的值；
（2）在直角坐标系内画出
函数y = bx + k的图象； （1）图象经过点（1，－2）的正比例函数的解析式；求满足下列条件的函数解析式：(4)已知直线y=kx+b的图象经过点（2，0），（4，3），（m，6），求m的值。(3)经过点（0，2）和（1，1）的直线的解析式(2)与直线y=－2x平行且经过点(1, -1)的直线的解析式； 1、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( ) ACBDD选一选2、一次函数y=ax-a的图象是( ). D选一选（1）（2）（3）（7）（5）（6）（4）（8）(1) (3) (4) (5) (6) (8)(3) (5)(1)(3)(6)(4)(5)(8)(1)(3)(6)(1)(8)选一选再见