第2章特殊三角形专题-- 勾股定理中的四类最短路径模型(含解析)
文档属性
| 名称 | 第2章特殊三角形专题-- 勾股定理中的四类最短路径模型(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题 勾股定理中的四类最短路径模型
勾股定理中的最短路线问题通常是以“两点之间,线段最短”为基本原理推出的。人们在生产、生活实践中,常常遇到带有某种限制条件的最近路线即最短路线问题。对于数学中的最短路线问题可以分为两大类:第一类为在同一平面内;第二类为空间几何体中的最短路线问题,对于平面内的最短路线问题可先画出方案图,然后确定最短距离及路径图。对于几何题内问题的关键是将立体图形转化为平面问题求解,然后构造直角三角形,利用勾股定理求解。
模型1.圆柱中的最短路径模型
【模型解读】圆柱体中最短路径基本模型如下:
计算跟圆柱有关的最短路径问题时,要注意圆柱的侧面展开图为矩形,利用两点之间线段最短结合勾股定理进行求解,注意展开后两个端点的位置,有时候需要用底面圆的周长进行计算,有时候需要用底面圆周长的一半进行计算。
注意:1)运用勾股定理计算最短路径时,按照展开—定点—连线—勾股定理的步骤进行计算;
2)缠绕类题型可以求出一圈的最短长度后乘以圈数。
【最值原理】两点之间线段最短。
例1.(2023·广东·八年级期中)如图,一个底面圆周长为24cm,高为9cm的圆柱体,一只蚂蚁从距离上边缘4cm的点A沿侧面爬行到相对的底面上的点B所经过的最短路线长为( )
A. B.15cm C.14cm D.13cm
例2.(2023·重庆·八年级期末)如图,圆柱形玻璃杯高,底面周长为,在外侧距下底处有一只蜘蛛,与蜘蛛相对的圆柱形容器的上端距开口处的外侧点处有一只苍蝇,蜘蛛捕到苍蝇的最短路线长是______.
例3.(2023春·山东济宁·八年级校考期中)春节期间,某广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为______米.
变式1.(2023·湖北十堰·统考一模)如图,这是一个供滑板爱好者使用的形池,该形池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是弧长为的半圆,其边缘(边缘的宽度忽略不计),点在上,一滑板爱好者从点滑到点,则他滑行的最短距离为( )
A. B. C. D.
变式2.(2023春·四川德阳·八年级校考期中)如图,圆柱底面半径为,高为,点A,B分别是圆柱两底面圆周上的点,且A,B在同一条竖直直线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为___________cm.
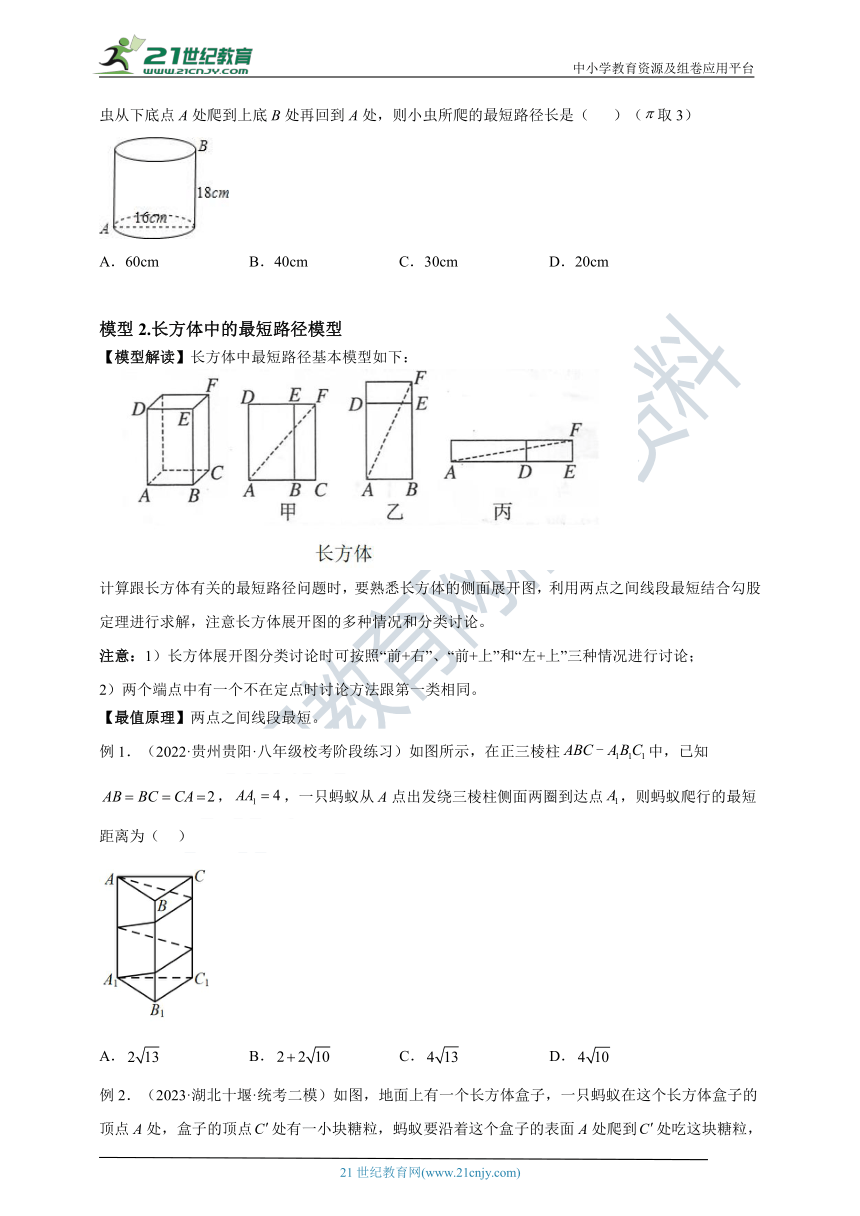
变式3.(2022·山东青岛·八年级期末)如图,一个圆桶,底面直径为16cm,高为18cm,则一只小虫从下底点A处爬到上底B处再回到A处,则小虫所爬的最短路径长是( )(取3)
A.60cm B.40cm C.30cm D.20cm
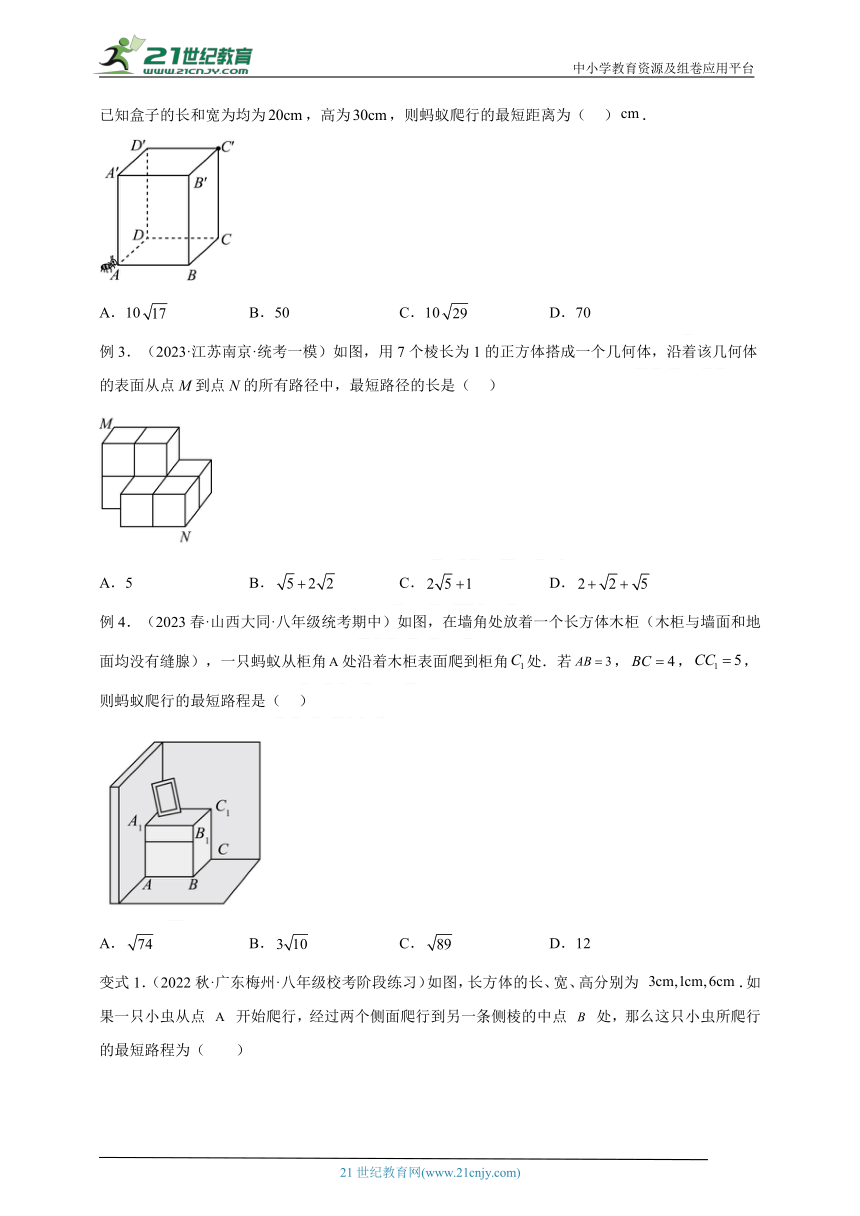
模型2.长方体中的最短路径模型
【模型解读】长方体中最短路径基本模型如下:
计算跟长方体有关的最短路径问题时,要熟悉长方体的侧面展开图,利用两点之间线段最短结合勾股定理进行求解,注意长方体展开图的多种情况和分类讨论。
注意:1)长方体展开图分类讨论时可按照“前+右”、“前+上”和“左+上”三种情况进行讨论;
2)两个端点中有一个不在定点时讨论方法跟第一类相同。
【最值原理】两点之间线段最短。
例1.(2022·贵州贵阳·八年级校考阶段练习)如图所示,在正三棱柱中,已知,,一只蚂蚁从A点出发绕三棱柱侧面两圈到达点,则蚂蚁爬行的最短距离为( )
A. B. C. D.
例2.(2023·湖北十堰·统考二模)如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到处吃这块糖粒,已知盒子的长和宽为均为,高为,则蚂蚁爬行的最短距离为( ).
A.10 B.50 C.10 D.70
例3.(2023·江苏南京·统考一模)如图,用7个棱长为1的正方体搭成一个几何体,沿着该几何体的表面从点M到点N的所有路径中,最短路径的长是( )
A.5 B. C. D.
例4.(2023春·山西大同·八年级统考期中)如图,在墙角处放着一个长方体木柜(木柜与墙面和地面均没有缝腺),一只蚂蚁从柜角处沿着木柜表面爬到柜角处.若,,,则蚂蚁爬行的最短路程是( )
A. B. C. D.12
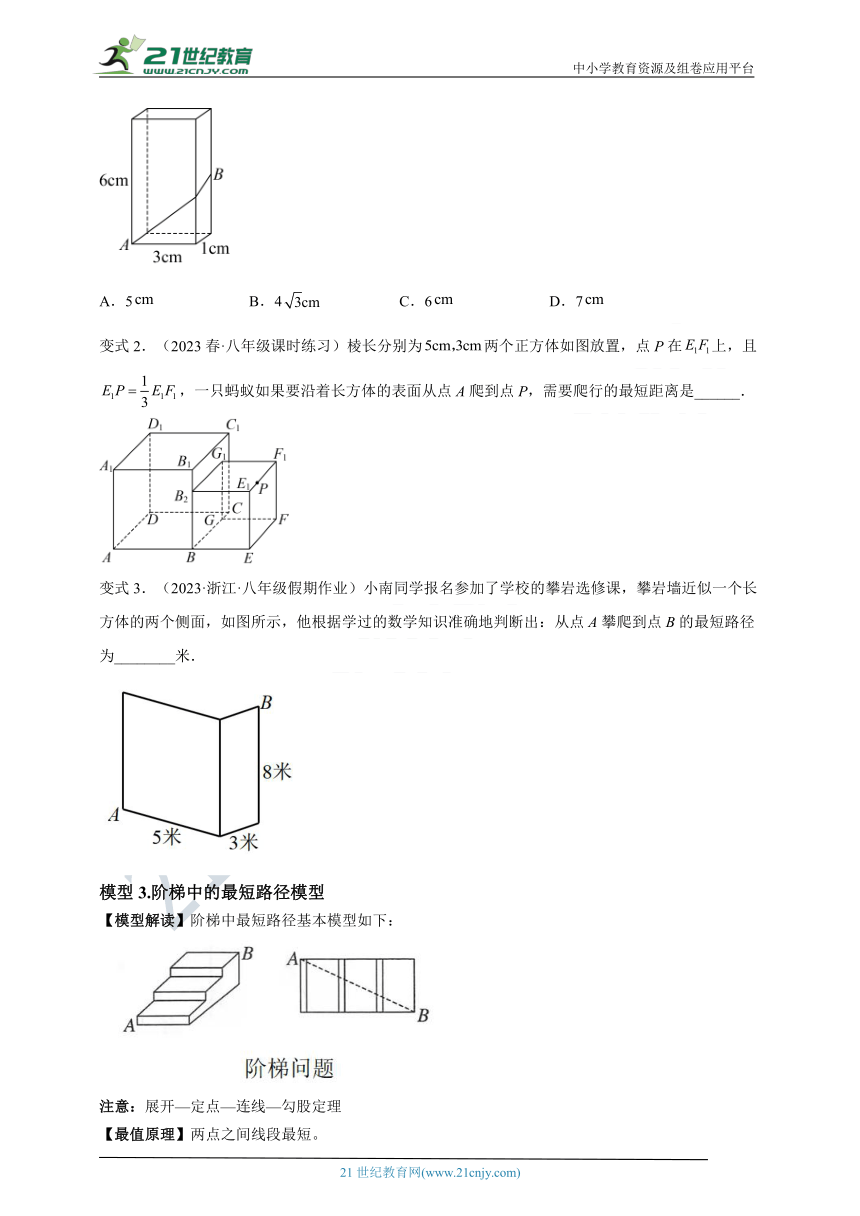
变式1.(2022秋·广东梅州·八年级校考阶段练习)如图,长方体的长、宽、高分别为 .如果一只小虫从点 开始爬行,经过两个侧面爬行到另一条侧棱的中点 处,那么这只小虫所爬行的最短路程为( )
A.5 B.4 C.6 D.7
变式2.(2023春·八年级课时练习)棱长分别为两个正方体如图放置,点P在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是______.
变式3.(2023·浙江·八年级假期作业)小南同学报名参加了学校的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为________米.
模型3.阶梯中的最短路径模型
【模型解读】阶梯中最短路径基本模型如下:
注意:展开—定点—连线—勾股定理
【最值原理】两点之间线段最短。
例1.(2023春·四川成都·九年级校考阶段练习)如图所示,是长方形地面,长,宽.中间竖有一堵砖墙高.一只蚂蚱从点爬到点,它必须翻过中间那堵墙,则它要走的路程s取值范围是________.
例2.(2023春·重庆八年级课时练习)在一个长为 米, 宽为 米的长方形草地 上, 如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽,木块的主视图是边长为 米的正三角形, 一只蚂蚁从 点处到处需要走的最短路程是______米.
变式1.(2023·陕西渭南·八年级统考期中)如图是一个二级台阶,每一级台阶的长、宽、高分别为、、.和是这个台阶两个相对的端点,在点有一只蚂蚁,想到点去受食,那么它爬行的最短路程是______.
变式2.(2023秋·四川宜宾·八年级统考期末)如图是一个三级台阶,它的每一级的长、宽、高分别是4米、0.7米、0.3米,A、B是这个台阶上两个相对的顶点,A点处有一只蚂蚁,它想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是________米.
模型4.将军饮马与最短路径模型
【模型解读】将军饮马与最短路径基本模型如下:
解决线段之和最小值问题:对称+连线,根据两点之间线段最短解决。
注意:立体图形中从外侧到内侧最短路径问题需要先作对称,再运用两点之间线段最短的原理结合勾股定理求解。
【最值原理】两点之间线段最短。
例1.(2023·四川广安·统考中考真题)如图,圆柱形玻璃杯的杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为___________.(杯壁厚度不计)
例2.(2022·陕西·八年级期中)有一个如图所示的长方体透明玻璃水缸,高,水深,在水面线上紧贴内壁处有一粒食物,且,一只小虫想从水缸外的处沿水缸壁爬到水缸内的处吃掉食物.(1)你认为小虫应该沿怎样的路线爬行才能使爬行的路线最短,请你画出它爬行的最短路线,并用箭头标注.(2)求小虫爬行的最短路线长(不计缸壁厚度).
例3.(2023春·河北保定·八年级统考期中)如图,高速公路的同一侧有A,B两城镇,它们到高速公路所在直线的距离分别为,,.要在高速公路上C,D之间建一个出口P,使A,B两城镇到P的距离之和最小,则这个最短距离为( )
A. B. C. D.
变式1.(2023春·湖北武汉·八年级校考阶段练习)如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿且与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( ).(杯壁厚度不计)
A.20 B.25 C.30 D.40
变式2.(2022·山东菏泽·八年级阶段练习)如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为的半圆,其边缘.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )m.(取3)
A.30 B.28 C.25 D.22
变式3.(2023春·广东八年级课时练习)如图,A,B两个村庄在河CD的同侧,两村庄的距离为a千米,,它们到河CD的距离分别是1千米和3千米.为了解决这两个村庄的饮水问题,乡政府决定在河CD边上修建一水厂向A,B两村输送水.(1)在图上作出向A,B两村铺设水管所用材料最省时的水厂位置M.(只需作图,不需要证明)。(2)经预算,修建水厂需20万元,铺设水管的所有费用平均每千米为3万元,其他费用需5万元,求完成这项工程乡政府投入的资金至少为多少万元.
课后专项训练
1.(2022·浙江金华初三月考)如图,圆柱底面半径为cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cm B.30cm C.2cm D.4cm
2.(2022·重庆八年级期中)如图,长方体的底面边长是1cm和3cm,高是6cm,如果用一根细线从点开始经过个侧面缠绕一圈到达,那么用细线最短需要( )
A.12cm B.10cm C.13cm D.11cm
3.(2022·山西八年级期末)如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
4.(2022·重庆初二月考)圆柱形杯子的高为18cm,底面周长为24cm,已知蚂蚁在外壁A处(距杯子上沿2cm)发现一滴蜂蜜在杯子内(距杯子下沿4cm),则蚂蚁从A处爬到B处的最短距离为( )
A. B.28 C.20 D.
5.(2023·广东惠州·八年级阶段练习)如图,是一块长、宽、高分别是、和的长方体木块,一只蚂蚁要从顶点出发,沿长方体的表面爬到和相对的顶点处吃食物,则它需要爬行的最短路线长是( ).
A. B.6 C. D.
6.(2023春·安徽·八年级期中)如图,圆柱形容器高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
A. B. C. D.
7.(2023秋·河南郑州·八年级校考期末)如图,一大楼的外墙面与地面垂直,点P在墙面上,若米,点P到的距离是8米,有一只蚂蚁要从点P爬到点B,它的最短行程是( )米.
A. B. C. D.
8.(2022秋·广东茂名·八年级校考期中)固定在地面上的一个正方体木块(如图①),其棱长为,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点A爬行到点B的最短路程为( )
A. B. C. D.
9.(2023·全国·八年级假期作业)如图是一个长方体盒子,其长、宽、高分别为4,2,9,用一根细线绕侧面绑在点A,B处,不计线头,细线的最短长度为( )
A.12 B.15 C.18 D.21
10.(2023春·成都市八年级课时练习)如图,在长方体盒子中,已知,长为的细直木棒恰好从小孔G处插入,木棒的一端I与底面接触,当木棒的端点I在长方形内及边界运动时,长度的最小值为( )
A. B. C. D.
11.(2022·陕西八年级期末)如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点处吃食物,那么它爬行的最短路程是___________.
12.(2021·重庆八年级期末)如图,三级台阶,每一级的长、宽、高分别为8dm、3dm、,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为______dm.
13.(2022·吉林长春·八年级期末)如图,有一个圆柱,底面圆的直径AB=cm,高BC=10cm,在BC的中点P处有一块蜂蜜,聪明的蚂蚁能够找到距离食物的最短路径,则蚂蚁从点A爬到点P的最短路程为 _____cm.
14.(2023春·安徽合肥·八年级校考期中)如图,正方体盒子的棱长为,O为的中点,现有一只蚂蚁位于点C处,它想沿正方体的表面爬行到点O处获取食物,则蚂蚁需爬行的最短路程为_______.
15.(2023春·安徽合肥·八年级合肥寿春中学校考期中)如图,一个圆柱形食品盒,它的高为,底面圆的周长为(1)点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物,则蚂蚁需要爬行的最短路程是______;
(2)将左图改为一个无盖的圆柱形食品盒,点C距离下底面,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如右图),则蚂蚁爬行的最短路程是___.
16.(2023秋·四川成都·八年级统考期末)小强家因装修准备用电梯搬运一些木条上楼,如图,已知电梯的长、宽、高分别是,,,那么电梯内能放入这些木条的最大长度是 ______
17.(2023·湖南永州·八年级校考阶段练习)如图是长、宽、高的长方体容器.(1)求底面矩形的对角线的长;(2)长方体容器内可完全放入的棍子最长是多少?
(3)一只蚂蚁从D点爬到E点最短路径是多少?
18.(2022秋·广东佛山·八年级统考期末)初中几何的学习始于空间的“实物和具体模型”,聚焦平面的“几何图形的特征和运用”,形成了空间几何问题要转化为平面几何问题的解题策略.
问题提出:如图所示是放在桌面上的一个圆柱体,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,如何求最短路程呢?(1)问题分析:蚂蚁从点出发沿着圆柱体的表面爬行到点,可以有几条路径?在图中画出来;(2)问题探究:①若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;②若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;③若圆柱体的底面圆的半径为,高为,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程.
19.(2022秋·广东深圳·八年级统考期末)如图,一个无盖长方体的小杯子放置在桌面上,,;(1)一只蚂蚁从点出发,沿小杯子外表面爬到点,求蚂蚁怎样走最短,最短路程是多少?
(2)为了怕杯子落入灰尘又方便使用,现在需要给杯子盖上盖子,并把一双筷子放进杯子里,请问,筷子的最大长度是多少?
20.(2023春·全国·八年级专题练习)我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点处缠绕而上.
(1)若绕五周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
(2)若绕周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
专题 勾股定理中的四类最短路径模型
勾股定理中的最短路线问题通常是以“两点之间,线段最短”为基本原理推出的。人们在生产、生活实践中,常常遇到带有某种限制条件的最近路线即最短路线问题。对于数学中的最短路线问题可以分为两大类:第一类为在同一平面内;第二类为空间几何体中的最短路线问题,对于平面内的最短路线问题可先画出方案图,然后确定最短距离及路径图。对于几何题内问题的关键是将立体图形转化为平面问题求解,然后构造直角三角形,利用勾股定理求解。
模型1.圆柱中的最短路径模型
【模型解读】圆柱体中最短路径基本模型如下:
计算跟圆柱有关的最短路径问题时,要注意圆柱的侧面展开图为矩形,利用两点之间线段最短结合勾股定理进行求解,注意展开后两个端点的位置,有时候需要用底面圆的周长进行计算,有时候需要用底面圆周长的一半进行计算。
注意:1)运用勾股定理计算最短路径时,按照展开—定点—连线—勾股定理的步骤进行计算;
2)缠绕类题型可以求出一圈的最短长度后乘以圈数。
【最值原理】两点之间线段最短。
例1.(2023·广东·八年级期中)如图,一个底面圆周长为24cm,高为9cm的圆柱体,一只蚂蚁从距离上边缘4cm的点A沿侧面爬行到相对的底面上的点B所经过的最短路线长为( )
A. B.15cm C.14cm D.13cm
【答案】D
【分析】将圆柱体展开,利用勾股定理进行求解即可.
【详解】解:将圆柱体的侧面展开,连接,如图所示:由于圆柱体的底面周长为24cm,
则, 又因为cm,所以(cm),
即蚂蚁沿表面从点A到点B所经过的最短路线长为13cm.故选:D.
【点睛】本题考查勾股定理的应用—最短路径问题.解题的关键是将立体图形展开为平面图形,利用勾股定理进行求解.
例2.(2023·重庆·八年级期末)如图,圆柱形玻璃杯高,底面周长为,在外侧距下底处有一只蜘蛛,与蜘蛛相对的圆柱形容器的上端距开口处的外侧点处有一只苍蝇,蜘蛛捕到苍蝇的最短路线长是______.
【答案】15
【分析】展开后连接,求出的长就是捕获苍蝇的蜘蛛所走的最短路径,过S作于E,求出、,根据勾股定理求出SF即可.
【详解】解:如图展开后连接,求出的长就是捕获苍蝇的蜘蛛所走的最短路径,
过S作于E,则(),(),
在中,由勾股定理得:(),故答案为15.
【点睛】本题考查勾股定理、平面展开-最短路线问题,关键是构造直角三角形,题目比较典型,难度适中.
例3.(2023春·山东济宁·八年级校考期中)春节期间,某广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为______米.
【答案】5
【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.
【详解】解:将圆柱表面切开展开呈长方形,则彩灯带长为2个长方形的对角线长,
圆柱高3米,底面周长2米,,,
每根柱子所用彩灯带的最短长度为.故答案为5.
【点睛】本题考查了平面展开最短路线问题,勾股定理的应用.圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
变式1.(2023·湖北十堰·统考一模)如图,这是一个供滑板爱好者使用的形池,该形池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是弧长为的半圆,其边缘(边缘的宽度忽略不计),点在上,一滑板爱好者从点滑到点,则他滑行的最短距离为( )
A. B. C. D.
【答案】C
【分析】滑行的距离最短,即是沿着的线段滑行,我们可将半圆展开为矩形来研究,展开后,、、三点构成直角三角形,为斜边,和为直角边,写出和的长,根据题意,由勾股定理即可得出的距离.
【详解】解:将半圆面展开可得:
米,米,
在中,(米).即滑行的最短距离为米.故选:C.
【点睛】本题考查了平面展开最短路径问题,型池的侧面展开图是一个矩形,此矩形的宽是半圆的弧长,矩形的长等于本题就是把型池的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
变式2.(2023春·四川德阳·八年级校考期中)如图,圆柱底面半径为,高为,点A,B分别是圆柱两底面圆周上的点,且A,B在同一条竖直直线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为___________cm.
【答案】15
【分析】要求圆柱体中两点之间的最短路径,最直接的作法,就是将圆柱体展开,然后利用两点之间线段最短解答.
【详解】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:;
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;∵圆柱底面半径为∴长方形的宽即是圆柱体的底面周长: ;
又∵圆柱高为,∴小长方形的一条边长是;
根据勾股定理求得;∴;故答案为:15.
【点睛】本题主要考查了平面展开--路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.
变式3.(2022·山东青岛·八年级期末)如图,一个圆桶,底面直径为16cm,高为18cm,则一只小虫从下底点A处爬到上底B处再回到A处,则小虫所爬的最短路径长是( )(取3)
A.60cm B.40cm C.30cm D.20cm
【答案】A
【分析】先将圆柱的侧面展开为一矩形,而矩形的长就是底面周长的一半,高就是圆柱的高,再根据勾股定理就可以求出其值.
【详解】解:展开圆柱的侧面如图,
根据两点之间线段最短就可以得知AB最短. 由题意,得AC=3×16÷2=24,
在Rt△ABC中,由勾股定理,得cm.
∵一只小虫从下底点A处爬到上底B处再回到A处,∴最短路径长为60cm.故选:A.
【点睛】本题考查了圆柱侧面展开图的运用,两点之间线段最短的运用,勾股定理的运用.在解答时将圆柱的侧面展开是关键.
模型2.长方体中的最短路径模型
【模型解读】长方体中最短路径基本模型如下:
计算跟长方体有关的最短路径问题时,要熟悉长方体的侧面展开图,利用两点之间线段最短结合勾股定理进行求解,注意长方体展开图的多种情况和分类讨论。
注意:1)长方体展开图分类讨论时可按照“前+右”、“前+上”和“左+上”三种情况进行讨论;
2)两个端点中有一个不在定点时讨论方法跟第一类相同。
【最值原理】两点之间线段最短。
例1.(2022·贵州贵阳·八年级校考阶段练习)如图所示,在正三棱柱中,已知,,一只蚂蚁从A点出发绕三棱柱侧面两圈到达点,则蚂蚁爬行的最短距离为( )
A. B. C. D.
【答案】D
【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将正三棱柱展开,然后利用两点之间线段最短解答.
【详解】∵一只蚂蚁从A点出发绕三棱柱侧面两圈到达点,
∴如图所示,将正三棱柱展开2次,∴,
∵正三棱柱的高∴.故选:D.
【点睛】此题考查了最短路径问题.解决本题的关键是熟练掌握用勾股定理的应用,要注意数形结合思想的应用.
例2.(2023·湖北十堰·统考二模)如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到处吃这块糖粒,已知盒子的长和宽为均为,高为,则蚂蚁爬行的最短距离为( ).
A.10 B.50 C.10 D.70
【答案】B
【分析】根据图形可知长方体的四个侧面都相等,所以分两种情况进行解答即可.
【详解】解:分两种情况:(其它情况与之重复)
①当蚂蚁从前面和右面爬过去时,如图1,连接,
在中,,,
根据勾股定理得:;
②当蚂蚁从前面和上面爬过去时,如图2,连接,
在中,,,
根据勾股定理得:;
蚂蚁爬行的最短距离为50.故选:B.
【点睛】本题考查了勾股定理的实际应用-求最短距离,读懂题意,熟悉立体图形的侧面展开图是解本题的关键.
例3.(2023·江苏南京·统考一模)如图,用7个棱长为1的正方体搭成一个几何体,沿着该几何体的表面从点M到点N的所有路径中,最短路径的长是( )
A.5 B. C. D.
【答案】A
【分析】先画出侧面展开图,根据两点之间践段最短,利用勾股定理求出线段的长即可.
【详解】将第一层小正方体的顶面和正面,以及第二层小正方体的顶面和正面展开,如下图,
连接,则最短路径,故选A
【点睛】本题主要考查了两点之间线段最短,以及勾股定理,正确画出侧面展开图,确定两点之间线段最短是解题的关键.
例4.(2023春·山西大同·八年级统考期中)如图,在墙角处放着一个长方体木柜(木柜与墙面和地面均没有缝腺),一只蚂蚁从柜角处沿着木柜表面爬到柜角处.若,,,则蚂蚁爬行的最短路程是( )
A. B. C. D.12
【答案】A
【分析】求出蚂蚁沿着木柜表面经线段到,以及蚂蚁沿着木柜表面经线段到的距离,再进行比较即可.
【详解】解:蚂蚁沿着木柜表面经线段到,爬过的路径的长是,
蚂蚁沿着木柜表面经线段到,爬过的路径的长是.
,最短路径的长是.故选A.
【点睛】此题主要考查了长方体展开图的对角线长度求法,这种题型经常在中考中出现,也是易错题型,希望能引起同学们的注意.
变式1.(2022秋·广东梅州·八年级校考阶段练习)如图,长方体的长、宽、高分别为 .如果一只小虫从点 开始爬行,经过两个侧面爬行到另一条侧棱的中点 处,那么这只小虫所爬行的最短路程为( )
A.5 B.4 C.6 D.7
【答案】A
【分析】根据题意把图形展开,连接,得出的长就是从处爬到处的最短路程,分为三种情况展开,根据勾股定理求出的长,再比较即可.
【详解】如图将正面与右面展开在同一平面,连接,由勾股定理得:,
如图将下底面与后面展开在同一平面,连接,由勾股定理得:,
如图将下底面与右面展开在同一平面,连接,由勾股定理得:,
∴从处爬到处的最短路程是,故选:.
【点睛】此题考查了立方体侧面展开图最短路径问题,解题关键是画出图形知道求出哪一条线段的长,题目具有一定的代表性,是一道比较好的题目,注意要进行分类讨论.
变式2.(2023春·八年级课时练习)棱长分别为两个正方体如图放置,点P在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是______.
【答案】cm.
【分析】求出两种展开图的值,比较即可判断;
【详解】解:如图,有两种展开方法:
方法一∶,方法二∶.
故需要爬行的最短距离是cm.故答案为:cm.
【点睛】本题考查平面展开-最短问题,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
变式3.(2023·浙江·八年级假期作业)小南同学报名参加了学校的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为________米.
【答案】
【分析】利用立体图形路径最小值为展开平面图的两点间距离,再根据勾股定理求解即可.
【详解】解:平面展开图为:
(米),故答案为.
【点睛】本题考查立体图形中两点间最短路径问题,通用办法是展开为平面图形,两点间最短路径为两点线段长度,利用水平距离和竖直距离得到直角三角形,勾股定理求出两点线段长度.熟悉立体图形中两点间最短路径问题的计算方法是解题的关键.
模型3.阶梯中的最短路径模型
【模型解读】阶梯中最短路径基本模型如下:
注意:展开—定点—连线—勾股定理
【最值原理】两点之间线段最短。
例1.(2023春·四川成都·九年级校考阶段练习)如图所示,是长方形地面,长,宽.中间竖有一堵砖墙高.一只蚂蚱从点爬到点,它必须翻过中间那堵墙,则它要走的路程s取值范围是________.
【答案】
【分析】连接,利用勾股定理求出的长,再把中间的墙平面展开,使原来的长方形长度增加而宽度不变,求出新长方形的对角线长即可得到范围.
【详解】解:如图所示,将图展开,图形长度增加,
原图长度增加,则,连接,
四边形是长方形,,宽,,
蚂蚱从点爬到点,它要走的路程.故答案为:.
【点睛】本题考查的是平面展开最短路线问题及勾股定理,根据题意画出图形是解答此题的关键.
例2.(2023春·重庆八年级课时练习)在一个长为 米, 宽为 米的长方形草地 上, 如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽,木块的主视图是边长为 米的正三角形, 一只蚂蚁从 点处到处需要走的最短路程是______米.
【答案】
【分析】如图,将木块展开,相当于长方形草地的长多了正三角形的一个边长,长方形的长为米,因为长方形的宽为3米,一只蚂蚁从点处到处需要走的最短路程是对角线,利用勾股定理求解即可.
【详解】解:如图,将木块展开,相当于长方形草地的长多了正三角形的一个边长,
长方形的长为米,
长方形的宽为3米,一只蚂蚁从点处到处需要走的最短路程是对角线,
米,故答案为.
【点睛】本题主要考查勾股定理的应用,根据题意将木块展开,再利用两点之间线段最短是解题关键.
变式1.(2023·陕西渭南·八年级统考期中)如图是一个二级台阶,每一级台阶的长、宽、高分别为、、.和是这个台阶两个相对的端点,在点有一只蚂蚁,想到点去受食,那么它爬行的最短路程是______.
【答案】
【分析】将台阶展开,得到一直角边长为,另一直角边为的直角三角形,求其斜边即可.
【详解】将台阶展开,得到一直角边长为,另一直角边为的直角三角形,
所以最短距离为,故答案为:.
【点睛】本题考查了几何体的展开图,勾股定理,熟练掌握展开图,勾股定理是解题的关键.
变式2.(2023秋·四川宜宾·八年级统考期末)如图是一个三级台阶,它的每一级的长、宽、高分别是4米、0.7米、0.3米,A、B是这个台阶上两个相对的顶点,A点处有一只蚂蚁,它想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是________米.
【答案】5
【分析】先将台阶展开,再根据勾股定理求解即可.
【详解】将三级台阶展开,如图所示.可知(米),(米),
根据两点之间线段最短,可知为最短路径,根据勾股定理得(米).
故答案为:5.
【点睛】本题考查了根据两点之间线段最短求最短路径,勾股定理等,勾股定理是求线段长的常用方法.
模型4.将军饮马与最短路径模型
【模型解读】将军饮马与最短路径基本模型如下:
解决线段之和最小值问题:对称+连线,根据两点之间线段最短解决。
注意:立体图形中从外侧到内侧最短路径问题需要先作对称,再运用两点之间线段最短的原理结合勾股定理求解。
【最值原理】两点之间线段最短。
例1.(2023·四川广安·统考中考真题)如图,圆柱形玻璃杯的杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为___________.(杯壁厚度不计)
【答案】10
【分析】如图(见解析),将玻璃杯侧面展开,作关于的对称点,根据两点之间线段最短可知的长度即为所求,利用勾股定理求解即可得.
【详解】解:如图,将玻璃杯侧面展开,作关于的对称点,作,交延长线于点,连接,
由题意得:,,
∵底面周长为,,,
由两点之间线段最短可知,蚂蚁从外壁处到内壁处所走的最短路程为,故答案为:10.
【点睛】本题考查了平面展开——最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
例2.(2022·陕西·八年级期中)有一个如图所示的长方体透明玻璃水缸,高,水深,在水面线上紧贴内壁处有一粒食物,且,一只小虫想从水缸外的处沿水缸壁爬到水缸内的处吃掉食物.(1)你认为小虫应该沿怎样的路线爬行才能使爬行的路线最短,请你画出它爬行的最短路线,并用箭头标注.(2)求小虫爬行的最短路线长(不计缸壁厚度).
【答案】(1)见解析;(2)100cm
【分析】(1)做出A关于BC的对称点A’,连接A’G,与BC交于点Q,由两点之间线段最短,此时A’G最短,即AQ+QG最短;(2)A’G为直角△A’EG的斜边,根据勾股定理求解即可.
【详解】解:(1)如下图所示,
作点A关于BC所在直线的对称点,连接,与交于点,
由两点之间线段最短,此时A’G最短,则为最短路线.
(2)∵,∴,∴.
在中,,,∴.
由对称性可知,∴.故小虫爬行的最短路线长为100cm.
【点睛】本题考查的是利用勾股定理求最短路径问题,本题的关键是根据对称性作出A的对称点A’,再根据两点之间线段最短,从而可找到路径求出解.
例3.(2023春·河北保定·八年级统考期中)如图,高速公路的同一侧有A,B两城镇,它们到高速公路所在直线的距离分别为,,.要在高速公路上C,D之间建一个出口P,使A,B两城镇到P的距离之和最小,则这个最短距离为( )
A. B. C. D.
【答案】B
【分析】根据题意画出图形,再利用轴对称求最短路径的方法得出点位置,进而结合勾股定理得出即可.
【详解】解:如图所示:作点关于直线的对称点,再连接,交直线于点
则此时最小,过点作延长线于点,
,,,,则,
在中,,则的最小值为:.故选:B.
【点睛】此题主要考查了应用与设计作图,两点之间线段最短、勾股定理等知识,解题的关键是学会利用对称解决最短问题.
变式1.(2023春·湖北武汉·八年级校考阶段练习)如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿且与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( ).(杯壁厚度不计)
A.20 B.25 C.30 D.40
【答案】B
【分析】化曲为直,利用勾股定理解决.
【详解】把玻璃杯的侧面展开,如图,把点A向上平移6cm到点C,连接,过点B作于D,由已知得:,,,
在中,由勾股定理得:,
则蚂蚁从外壁A处到内壁B处的最短距离为.故选:B
【点睛】本题考查了勾股定理的应用,根据题意把圆柱展开,化曲为直是解决问题的关键.
变式2.(2022·山东菏泽·八年级阶段练习)如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为的半圆,其边缘.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )m.(取3)
A.30 B.28 C.25 D.22
【答案】C
【分析】根据题意画出侧面展开图,作点C关于AB的对称点F,连接DF,根据半圆的周长求得,根据对称求得,在Rt△CDF中,勾股定理求得.
【详解】其侧面展开图如图:作点C关于AB的对称点F,连接DF,
∵中间可供滑行的部分的截面是半径为2.5cm的半圆,
∴BC=πR=2.5π=7.5cm,AB=CD=20cm,∴CF=2BC=15cm,
在Rt△CDF中,DF=cm,故他滑行的最短距离约为cm.故选C.
【点睛】本题考查了勾股定理最短路径问题,作出侧面展开图是解题的关键.
变式3.(2023春·广东八年级课时练习)如图,A,B两个村庄在河CD的同侧,两村庄的距离为a千米,,它们到河CD的距离分别是1千米和3千米.为了解决这两个村庄的饮水问题,乡政府决定在河CD边上修建一水厂向A,B两村输送水.(1)在图上作出向A,B两村铺设水管所用材料最省时的水厂位置M.(只需作图,不需要证明)。(2)经预算,修建水厂需20万元,铺设水管的所有费用平均每千米为3万元,其他费用需5万元,求完成这项工程乡政府投入的资金至少为多少万元.
【答案】(1)见解析;(2)50万元.
【分析】(1)作点A关于直线的对称点,连接,交于M点,即M为所求;
(2)连接交于H点,过点B作,根据勾股定理求出,即可得出答案.
【详解】(1)解:如图,作点A关于直线的对称点,连接,交于M点,即M为所求.
(2)解:如图,连接交于H点,过点B作,
由题意可知:,,,
∴,
∴在中,,
∴在中,,
由对称性质可知:,水管长,
完成这项工程乡政府投入的资金至少为(万元)
【点睛】本题考查了轴对称最短路线问题,勾股定理,题目比较典型,是一道比较好的题目,考查了学生的动手操作能力和计算能力.
课后专项训练
1.(2022·浙江金华初三月考)如图,圆柱底面半径为cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cm B.30cm C.2cm D.4cm
【答案】B
【分析】要求圆柱体中两点之间的最短路径,最直接的作法,就是将圆柱体展开,然后利用两点之间线段最短解答.
【解析】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;∵圆柱底面半径为cm,∴长方形的宽即是圆柱体的底面周长:2π×=8cm;
又∵圆柱高为18cm,∴小长方形的一条边长是6cm;
根据勾股定理求得AC=CD=DB=10cm;∴AC+CD+DB=30cm;故选:B.
【点睛】本题主要考查了圆柱的计算、平面展开 路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.
2.(2022·重庆八年级期中)如图,长方体的底面边长是1cm和3cm,高是6cm,如果用一根细线从点开始经过个侧面缠绕一圈到达,那么用细线最短需要( )
A.12cm B.10cm C.13cm D.11cm
【答案】B
【分析】要求所用细线的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”,利用勾股定理求出所需结果.
【详解】解:如图,将长方体展开,连接A、B′,则AA′=1+3+1+3=8(cm), A′B′=6cm,
根据两点之间线段最短,由勾股定理得:AB′2=AA′2+A′B′2=82+62=102cm,所以AB′=10 cm.故选:B.
【点睛】本题考查了平面展开 最短路径问题,本题的关键是把长方体的侧面展开“化立体为平面”,构造直角三角形运用勾股定理解决.
3.(2022·山西八年级期末)如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
【答案】D
【分析】将题中图案展开后,连接AC,利用勾股定理可得AC长,将中间的墙展开在平面上,则原矩形长度增加宽度不变,求出新矩形的对角线长即为所求.
【详解】解:展开如图得新矩形,连接AC,则其长度至少增加2MN,宽度不变,
由此可得:,
根据勾股定理有:故选D.
【点睛】本题考查平面展开图形最短路线问题以及勾股定理得应用;解题关键在于根据题意画出正确的平面展开图.
4.(2022·重庆初二月考)圆柱形杯子的高为18cm,底面周长为24cm,已知蚂蚁在外壁A处(距杯子上沿2cm)发现一滴蜂蜜在杯子内(距杯子下沿4cm),则蚂蚁从A处爬到B处的最短距离为( )
A. B.28 C.20 D.
【答案】C
分析:将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
【解析】如图所示,将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B= (cm)故选C.
点睛:本题考查了勾股定理、最短路径等知识.将圆柱侧面展开,化曲面为平面并作出A关于EF的对称点A′是解题的关键.
5.(2023·广东惠州·八年级阶段练习)如图,是一块长、宽、高分别是、和的长方体木块,一只蚂蚁要从顶点出发,沿长方体的表面爬到和相对的顶点处吃食物,则它需要爬行的最短路线长是( ).
A. B.6 C. D.
【答案】A
【分析】根据长方体的侧面展开计算:沿前表面和上表面所构成矩形的对角线爬行距离,沿前表面和右表面所构成矩形的对角线爬行距离,沿左表面和上表面所构成矩形的对角线爬行距离,沿左表面和后表面所构成矩形的对角线爬行距离,再比较大小即可;
【详解】解:如图1,当蚂蚁由点经前表面和上表面所构成矩形的对角线到达点时,
由勾股定理可得,
如图2,当蚂蚁由点经前表面和右表面所构成矩形的对角线到达点时,
由勾股定理可得,
如图3,当蚂蚁由点经左表面和上表面所构成矩形的对角线到达点时,
由勾股定理可得,
如图4,当蚂蚁由点经左表面和后表面所构成矩形的对角线到达点时,
由勾股定理可得,∵,故选: A.
【点睛】本题考查了长方体的侧面展开,两点间的最短距离,勾股定理;根据长方体的侧面展开分类讨论是解题关键.
6.(2023春·安徽·八年级期中)如图,圆柱形容器高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
A. B. C. D.
【答案】C
【分析】将圆柱侧面展开,如图所示,作出A点关于的对称点,连接,根据两点之间线段最短,可知即为最短距离,然后根据勾股定理求解.
【详解】解:将圆柱侧面展开,如图所示,作出A点关于的对称点,过点B作于点C,
∵形容器高为,点A处离杯上沿,点B处离杯底,
∴,,∴,
∵底面周长为,∴,
根据勾股定理可得:,故选:C.
【点睛】本题考查平面展开,最短路径问题,将图形展开,利用轴对称的性质找出最短路径是解题的关键.
7.(2023秋·河南郑州·八年级校考期末)如图,一大楼的外墙面与地面垂直,点P在墙面上,若米,点P到的距离是8米,有一只蚂蚁要从点P爬到点B,它的最短行程是( )米.
A. B. C. D.
【答案】D
【分析】可将教室的墙面与地面展开,连接,根据两点之间线段最短,利用勾股定理求解即可.
【详解】解:如图,过P作于G,连接,
(米),(米),(米),
(米),(米)
这只蚂蚁的最短行程应该是米,故选:D.
【点睛】本题主要考查了平面展开-最短路径问题,解题关键是立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决.
8.(2022秋·广东茂名·八年级校考期中)固定在地面上的一个正方体木块(如图①),其棱长为,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点A爬行到点B的最短路程为( )
A. B. C. D.
【答案】A
【分析】根据两点之间线段最短,将图②展开,利用勾股定理进行求解即可.
【详解】解:如图,正方体上表面的对角线为,将图②展开,连接交于点,线段的长度即为蚂蚁爬行的最短路程,
由题意可知:为等边三角形,为等腰直角三角形,
∵,∴,∴,∴,
∵正方体的棱长为,∴,,
在中,,在中,,
∴;故选A.
【点睛】本题考查勾股定理的应用.解题关键是将立体图像展开,根据两点之间线段最短,确定最短路径.
9.(2023·全国·八年级假期作业)如图是一个长方体盒子,其长、宽、高分别为4,2,9,用一根细线绕侧面绑在点A,B处,不计线头,细线的最短长度为( )
A.12 B.15 C.18 D.21
【答案】B
【分析】把长方体沿边剪开,再根据勾股定理计算即可.
【详解】如图所示,连接,则即为所求的最短长度,,
在中,故选:B.
【点睛】本题主要考查了勾股定理的应用,把长方体沿边剪开得到矩形是解题的关键.
10.(2023春·成都市八年级课时练习)如图,在长方体盒子中,已知,长为的细直木棒恰好从小孔G处插入,木棒的一端I与底面接触,当木棒的端点I在长方形内及边界运动时,长度的最小值为( )
A. B. C. D.
【答案】A
【分析】当最大时,最小,当I运动到点A时,最大,根据勾股定理求解即可.
【详解】解:当最大时,最小,当I运动到点A时,最大,
此时,而,
∴,∴长度的最小值为.故选:A.
【点睛】本题考查了勾股定理的应用,根据勾股定理求出的最大值是解题的关键.
11.(2022·陕西八年级期末)如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点处吃食物,那么它爬行的最短路程是___________.
【答案】5
【分析】利用平面展开图有3种情况,画出图形利用勾股定理求出MN的长即可.
【详解】解:分三种情况:如图1,,
如图2,,∴AP=5, 如图3,,
, 它爬行的最短路程为5,故答案为:5.
,
【点睛】此题考查平面展开图最短路径问题和勾股定理应用,利用展开图有3种情况分析得出是解题关键.
12.(2021·重庆八年级期末)如图,三级台阶,每一级的长、宽、高分别为8dm、3dm、,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为______dm.
【答案】17
【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.
【详解】解:三级台阶平面展开图为长方形,长为8dm,宽为,
则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.可设蚂蚁沿台阶面爬行到B点最短路程为xdm,
由勾股定理得:,解得.故答案为:17.
【点睛】本题考查了平面展开最短路径问题,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.
13.(2022·吉林长春·八年级期末)如图,有一个圆柱,底面圆的直径AB=cm,高BC=10cm,在BC的中点P处有一块蜂蜜,聪明的蚂蚁能够找到距离食物的最短路径,则蚂蚁从点A爬到点P的最短路程为 _____cm.
【答案】13
【分析】化“曲”为“平”,在平面内,得到两点的位置,再根据两点之间线段最短和勾股定理求解即可.
【详解】将圆柱体的侧面展开,如图所示:
AB=底面周长=××=12(cm),BP=BC=5(cm),所以AP=(cm),
故蚂蚁从A点爬到P点的最短距离为13cm,故答案为:13.
【点睛】本题考查最短距离问题,化“曲”为“平”,在平面内,利用两点之间线段最短和勾股定理是常用求解方法.
14.(2023春·安徽合肥·八年级校考期中)如图,正方体盒子的棱长为,O为的中点,现有一只蚂蚁位于点C处,它想沿正方体的表面爬行到点O处获取食物,则蚂蚁需爬行的最短路程为_______.
【答案】
【分析】根据两点之间线段最短,用勾股定理求解.
【详解】解:如图,连接,则线段的长就是蚂蚁需爬行的最短路程,
∵正方体的棱长为,O为的中点,∴,,,
由勾股定理得,
答:蚂蚁需爬行的最短路程为,故答案为:.
【点睛】本题考查两点之间线段最短,灵活运用所学知识是关键.
15.(2023春·安徽合肥·八年级合肥寿春中学校考期中)如图,一个圆柱形食品盒,它的高为,底面圆的周长为
(1)点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物,则蚂蚁需要爬行的最短路程是______;
(2)将左图改为一个无盖的圆柱形食品盒,点C距离下底面,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如右图),则蚂蚁爬行的最短路程是___.
【答案】
【分析】(1)把圆柱侧面展开,在中,利用勾股定理求解即可.
(2)将圆柱侧面展开,得到矩形,作点关于的对称点,构造,根据勾股定理求出即可解决问题.
【详解】(1)如图,把圆柱侧面展开,在中,
∵,∴ ,故答案为:.
(2)如图所示,点与点关于对称,可得,,
则最短路程为故答案为:.
【点睛】本题考查了勾股定理求线段最短距离,轴对称的性质,熟练掌握勾股定理是解题的关键.
16.(2023秋·四川成都·八年级统考期末)小强家因装修准备用电梯搬运一些木条上楼,如图,已知电梯的长、宽、高分别是,,,那么电梯内能放入这些木条的最大长度是 ______
【答案】
【分析】由勾股定理求出,再由勾股定理求出即可.
【详解】如图所示:
由勾股定理知:,,
即电梯内能放入这些木条的最大长度是.故答案为:.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理,并能进行推理计算是解决问题的关键.
17.(2023·湖南永州·八年级校考阶段练习)如图是长、宽、高的长方体容器.
(1)求底面矩形的对角线的长;(2)长方体容器内可完全放入的棍子最长是多少?
(3)一只蚂蚁从D点爬到E点最短路径是多少?
【答案】(1)底面矩形的对角线的长为(2)长方体容器内可完全放入的棍子最长是
(3)蚂蚁从D点爬到E点最短路径
【分析】(1)根据题意运用勾股定理即可得出结果;(2)根据题意连接、,两次运用勾股定理即可得出结果;(3)分别求出三种情况下蚂蚁爬行的最短距离,然后进行比较,得出蚂蚁爬行的最短距离即可.
【详解】(1)解:∵、,,∴对角线的长为:;
答:底面矩形的对角线的长为.
(2)解:连接、,如图所示:
在中,∵、,,∴,
在中, .答:这个盒子最长能放的棍子.
(3)解:将前面的面和右边的面展开,如图所示:
此时蚂蚁从D点爬到E点最短路径为:;
将前面的面和上边的面展开,如图所示:
此时蚂蚁从D点爬到E点最短路径为:;
将左边的面和上边的面展开,如图所示:
此时蚂蚁从D点爬到E点最短路径为:;
∵,∴蚂蚁从D点爬到E点最短路径.
【点睛】本题考查的是勾股定理的应用,根据题意,作出辅助线、构造出直角三角形是解答此题的关键.
18.(2022秋·广东佛山·八年级统考期末)初中几何的学习始于空间的“实物和具体模型”,聚焦平面的“几何图形的特征和运用”,形成了空间几何问题要转化为平面几何问题的解题策略.
问题提出:如图所示是放在桌面上的一个圆柱体,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,如何求最短路程呢?(1)问题分析:蚂蚁从点出发沿着圆柱体的表面爬行到点,可以有几条路径?在图中画出来;(2)问题探究:①若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;②若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;③若圆柱体的底面圆的半径为,高为,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程.
【答案】(1)3条,图形见解析 (2)①;②;③
【分析】(1)共有3条路径,第一条先沿圆柱体的高爬行,再从上底面边缘爬行;第二条先沿圆柱体的高爬行,再从上底面直径爬行;第三条沿圆柱体侧面爬行,即可;
(2)①连接,利用两点之间,线段最短,在中,根据勾股定理,求出的长,即可求解;②利用两点之间,线段最短,在中,根据勾股定理,求出的长,即可求解;③利用两点之间,线段最短,在中,根据勾股定理,求出的长,即可求解.
【详解】(1)解:共有3条路径,如下图:
(2)解:①如图,连接,根据题意得:,,∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为;
②如图,连接, 根据题意得:,,∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为;
③如图,连接, 根据题意得:,,∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为.
【点睛】本题主要考查了勾股定理的实际应用,熟练掌握勾股定理是解题的关键.
19.(2022秋·广东深圳·八年级统考期末)如图,一个无盖长方体的小杯子放置在桌面上,,;
(1)一只蚂蚁从点出发,沿小杯子外表面爬到点,求蚂蚁怎样走最短,最短路程是多少?
(2)为了怕杯子落入灰尘又方便使用,现在需要给杯子盖上盖子,并把一双筷子放进杯子里,请问,筷子的最大长度是多少?
【答案】(1)如方法一的路线最短,最短路线为(2)筷子的最大长度是
【分析】(1)分别讨论将面和面展开,将面和上底面展开两种情况,再利用勾股定理计算,进而比较即可求解;
(2)当筷子沿倾斜放的时候,能够放的最长,利用勾股定理计算即可.
【详解】(1)方法一:将面和面展开,如图,
∵,,∴,
由勾股定理得;
方法二:将面和上底面展开,如图,
∵,,∴,
由勾股定理得;
所以,如方法一的路线最短,最短路线为;
(2)如图,当筷子沿倾斜放的时候,能够放的最长,
∵,,∴由勾股定理得,
∴,所以,筷子的最大长度是.
【点睛】本题考查了勾股定理的应用,准确理解题意,熟练掌握勾股定理是解题的关键.
20.(2023春·全国·八年级专题练习)我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点处缠绕而上.
(1)若绕五周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
(2)若绕周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
【答案】(1)25(2)
【分析】(1)根据题意画出图形,在Rt中,再根据勾股定理求解即可;
(2)在Rt中根据勾股定理求解即可.
【详解】(1)解:如图所示,
在Rt中,,,(尺)
答:葛藤长为25尺.故答案为:25;
(2)解:在Rt中,,,
(尺),
答:葛藤长为尺.故答案为:.
【点睛】本题考查的是平面展开—最短路径问题,能够根据题意画出图形,构造出直角三角形是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题 勾股定理中的四类最短路径模型
勾股定理中的最短路线问题通常是以“两点之间,线段最短”为基本原理推出的。人们在生产、生活实践中,常常遇到带有某种限制条件的最近路线即最短路线问题。对于数学中的最短路线问题可以分为两大类:第一类为在同一平面内;第二类为空间几何体中的最短路线问题,对于平面内的最短路线问题可先画出方案图,然后确定最短距离及路径图。对于几何题内问题的关键是将立体图形转化为平面问题求解,然后构造直角三角形,利用勾股定理求解。
模型1.圆柱中的最短路径模型
【模型解读】圆柱体中最短路径基本模型如下:
计算跟圆柱有关的最短路径问题时,要注意圆柱的侧面展开图为矩形,利用两点之间线段最短结合勾股定理进行求解,注意展开后两个端点的位置,有时候需要用底面圆的周长进行计算,有时候需要用底面圆周长的一半进行计算。
注意:1)运用勾股定理计算最短路径时,按照展开—定点—连线—勾股定理的步骤进行计算;
2)缠绕类题型可以求出一圈的最短长度后乘以圈数。
【最值原理】两点之间线段最短。
例1.(2023·广东·八年级期中)如图,一个底面圆周长为24cm,高为9cm的圆柱体,一只蚂蚁从距离上边缘4cm的点A沿侧面爬行到相对的底面上的点B所经过的最短路线长为( )
A. B.15cm C.14cm D.13cm
例2.(2023·重庆·八年级期末)如图,圆柱形玻璃杯高,底面周长为,在外侧距下底处有一只蜘蛛,与蜘蛛相对的圆柱形容器的上端距开口处的外侧点处有一只苍蝇,蜘蛛捕到苍蝇的最短路线长是______.
例3.(2023春·山东济宁·八年级校考期中)春节期间,某广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为______米.
变式1.(2023·湖北十堰·统考一模)如图,这是一个供滑板爱好者使用的形池,该形池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是弧长为的半圆,其边缘(边缘的宽度忽略不计),点在上,一滑板爱好者从点滑到点,则他滑行的最短距离为( )
A. B. C. D.
变式2.(2023春·四川德阳·八年级校考期中)如图,圆柱底面半径为,高为,点A,B分别是圆柱两底面圆周上的点,且A,B在同一条竖直直线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为___________cm.
变式3.(2022·山东青岛·八年级期末)如图,一个圆桶,底面直径为16cm,高为18cm,则一只小虫从下底点A处爬到上底B处再回到A处,则小虫所爬的最短路径长是( )(取3)
A.60cm B.40cm C.30cm D.20cm
模型2.长方体中的最短路径模型
【模型解读】长方体中最短路径基本模型如下:
计算跟长方体有关的最短路径问题时,要熟悉长方体的侧面展开图,利用两点之间线段最短结合勾股定理进行求解,注意长方体展开图的多种情况和分类讨论。
注意:1)长方体展开图分类讨论时可按照“前+右”、“前+上”和“左+上”三种情况进行讨论;
2)两个端点中有一个不在定点时讨论方法跟第一类相同。
【最值原理】两点之间线段最短。
例1.(2022·贵州贵阳·八年级校考阶段练习)如图所示,在正三棱柱中,已知,,一只蚂蚁从A点出发绕三棱柱侧面两圈到达点,则蚂蚁爬行的最短距离为( )
A. B. C. D.
例2.(2023·湖北十堰·统考二模)如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到处吃这块糖粒,已知盒子的长和宽为均为,高为,则蚂蚁爬行的最短距离为( ).
A.10 B.50 C.10 D.70
例3.(2023·江苏南京·统考一模)如图,用7个棱长为1的正方体搭成一个几何体,沿着该几何体的表面从点M到点N的所有路径中,最短路径的长是( )
A.5 B. C. D.
例4.(2023春·山西大同·八年级统考期中)如图,在墙角处放着一个长方体木柜(木柜与墙面和地面均没有缝腺),一只蚂蚁从柜角处沿着木柜表面爬到柜角处.若,,,则蚂蚁爬行的最短路程是( )
A. B. C. D.12
变式1.(2022秋·广东梅州·八年级校考阶段练习)如图,长方体的长、宽、高分别为 .如果一只小虫从点 开始爬行,经过两个侧面爬行到另一条侧棱的中点 处,那么这只小虫所爬行的最短路程为( )
A.5 B.4 C.6 D.7
变式2.(2023春·八年级课时练习)棱长分别为两个正方体如图放置,点P在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是______.
变式3.(2023·浙江·八年级假期作业)小南同学报名参加了学校的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为________米.
模型3.阶梯中的最短路径模型
【模型解读】阶梯中最短路径基本模型如下:
注意:展开—定点—连线—勾股定理
【最值原理】两点之间线段最短。
例1.(2023春·四川成都·九年级校考阶段练习)如图所示,是长方形地面,长,宽.中间竖有一堵砖墙高.一只蚂蚱从点爬到点,它必须翻过中间那堵墙,则它要走的路程s取值范围是________.
例2.(2023春·重庆八年级课时练习)在一个长为 米, 宽为 米的长方形草地 上, 如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽,木块的主视图是边长为 米的正三角形, 一只蚂蚁从 点处到处需要走的最短路程是______米.
变式1.(2023·陕西渭南·八年级统考期中)如图是一个二级台阶,每一级台阶的长、宽、高分别为、、.和是这个台阶两个相对的端点,在点有一只蚂蚁,想到点去受食,那么它爬行的最短路程是______.
变式2.(2023秋·四川宜宾·八年级统考期末)如图是一个三级台阶,它的每一级的长、宽、高分别是4米、0.7米、0.3米,A、B是这个台阶上两个相对的顶点,A点处有一只蚂蚁,它想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是________米.
模型4.将军饮马与最短路径模型
【模型解读】将军饮马与最短路径基本模型如下:
解决线段之和最小值问题:对称+连线,根据两点之间线段最短解决。
注意:立体图形中从外侧到内侧最短路径问题需要先作对称,再运用两点之间线段最短的原理结合勾股定理求解。
【最值原理】两点之间线段最短。
例1.(2023·四川广安·统考中考真题)如图,圆柱形玻璃杯的杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为___________.(杯壁厚度不计)
例2.(2022·陕西·八年级期中)有一个如图所示的长方体透明玻璃水缸,高,水深,在水面线上紧贴内壁处有一粒食物,且,一只小虫想从水缸外的处沿水缸壁爬到水缸内的处吃掉食物.(1)你认为小虫应该沿怎样的路线爬行才能使爬行的路线最短,请你画出它爬行的最短路线,并用箭头标注.(2)求小虫爬行的最短路线长(不计缸壁厚度).
例3.(2023春·河北保定·八年级统考期中)如图,高速公路的同一侧有A,B两城镇,它们到高速公路所在直线的距离分别为,,.要在高速公路上C,D之间建一个出口P,使A,B两城镇到P的距离之和最小,则这个最短距离为( )
A. B. C. D.
变式1.(2023春·湖北武汉·八年级校考阶段练习)如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿且与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( ).(杯壁厚度不计)
A.20 B.25 C.30 D.40
变式2.(2022·山东菏泽·八年级阶段练习)如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为的半圆,其边缘.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )m.(取3)
A.30 B.28 C.25 D.22
变式3.(2023春·广东八年级课时练习)如图,A,B两个村庄在河CD的同侧,两村庄的距离为a千米,,它们到河CD的距离分别是1千米和3千米.为了解决这两个村庄的饮水问题,乡政府决定在河CD边上修建一水厂向A,B两村输送水.(1)在图上作出向A,B两村铺设水管所用材料最省时的水厂位置M.(只需作图,不需要证明)。(2)经预算,修建水厂需20万元,铺设水管的所有费用平均每千米为3万元,其他费用需5万元,求完成这项工程乡政府投入的资金至少为多少万元.
课后专项训练
1.(2022·浙江金华初三月考)如图,圆柱底面半径为cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cm B.30cm C.2cm D.4cm
2.(2022·重庆八年级期中)如图,长方体的底面边长是1cm和3cm,高是6cm,如果用一根细线从点开始经过个侧面缠绕一圈到达,那么用细线最短需要( )
A.12cm B.10cm C.13cm D.11cm
3.(2022·山西八年级期末)如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
4.(2022·重庆初二月考)圆柱形杯子的高为18cm,底面周长为24cm,已知蚂蚁在外壁A处(距杯子上沿2cm)发现一滴蜂蜜在杯子内(距杯子下沿4cm),则蚂蚁从A处爬到B处的最短距离为( )
A. B.28 C.20 D.
5.(2023·广东惠州·八年级阶段练习)如图,是一块长、宽、高分别是、和的长方体木块,一只蚂蚁要从顶点出发,沿长方体的表面爬到和相对的顶点处吃食物,则它需要爬行的最短路线长是( ).
A. B.6 C. D.
6.(2023春·安徽·八年级期中)如图,圆柱形容器高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
A. B. C. D.
7.(2023秋·河南郑州·八年级校考期末)如图,一大楼的外墙面与地面垂直,点P在墙面上,若米,点P到的距离是8米,有一只蚂蚁要从点P爬到点B,它的最短行程是( )米.
A. B. C. D.
8.(2022秋·广东茂名·八年级校考期中)固定在地面上的一个正方体木块(如图①),其棱长为,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点A爬行到点B的最短路程为( )
A. B. C. D.
9.(2023·全国·八年级假期作业)如图是一个长方体盒子,其长、宽、高分别为4,2,9,用一根细线绕侧面绑在点A,B处,不计线头,细线的最短长度为( )
A.12 B.15 C.18 D.21
10.(2023春·成都市八年级课时练习)如图,在长方体盒子中,已知,长为的细直木棒恰好从小孔G处插入,木棒的一端I与底面接触,当木棒的端点I在长方形内及边界运动时,长度的最小值为( )
A. B. C. D.
11.(2022·陕西八年级期末)如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点处吃食物,那么它爬行的最短路程是___________.
12.(2021·重庆八年级期末)如图,三级台阶,每一级的长、宽、高分别为8dm、3dm、,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为______dm.
13.(2022·吉林长春·八年级期末)如图,有一个圆柱,底面圆的直径AB=cm,高BC=10cm,在BC的中点P处有一块蜂蜜,聪明的蚂蚁能够找到距离食物的最短路径,则蚂蚁从点A爬到点P的最短路程为 _____cm.
14.(2023春·安徽合肥·八年级校考期中)如图,正方体盒子的棱长为,O为的中点,现有一只蚂蚁位于点C处,它想沿正方体的表面爬行到点O处获取食物,则蚂蚁需爬行的最短路程为_______.
15.(2023春·安徽合肥·八年级合肥寿春中学校考期中)如图,一个圆柱形食品盒,它的高为,底面圆的周长为(1)点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物,则蚂蚁需要爬行的最短路程是______;
(2)将左图改为一个无盖的圆柱形食品盒,点C距离下底面,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如右图),则蚂蚁爬行的最短路程是___.
16.(2023秋·四川成都·八年级统考期末)小强家因装修准备用电梯搬运一些木条上楼,如图,已知电梯的长、宽、高分别是,,,那么电梯内能放入这些木条的最大长度是 ______
17.(2023·湖南永州·八年级校考阶段练习)如图是长、宽、高的长方体容器.(1)求底面矩形的对角线的长;(2)长方体容器内可完全放入的棍子最长是多少?
(3)一只蚂蚁从D点爬到E点最短路径是多少?
18.(2022秋·广东佛山·八年级统考期末)初中几何的学习始于空间的“实物和具体模型”,聚焦平面的“几何图形的特征和运用”,形成了空间几何问题要转化为平面几何问题的解题策略.
问题提出:如图所示是放在桌面上的一个圆柱体,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,如何求最短路程呢?(1)问题分析:蚂蚁从点出发沿着圆柱体的表面爬行到点,可以有几条路径?在图中画出来;(2)问题探究:①若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;②若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;③若圆柱体的底面圆的半径为,高为,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程.
19.(2022秋·广东深圳·八年级统考期末)如图,一个无盖长方体的小杯子放置在桌面上,,;(1)一只蚂蚁从点出发,沿小杯子外表面爬到点,求蚂蚁怎样走最短,最短路程是多少?
(2)为了怕杯子落入灰尘又方便使用,现在需要给杯子盖上盖子,并把一双筷子放进杯子里,请问,筷子的最大长度是多少?
20.(2023春·全国·八年级专题练习)我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点处缠绕而上.
(1)若绕五周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
(2)若绕周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
专题 勾股定理中的四类最短路径模型
勾股定理中的最短路线问题通常是以“两点之间,线段最短”为基本原理推出的。人们在生产、生活实践中,常常遇到带有某种限制条件的最近路线即最短路线问题。对于数学中的最短路线问题可以分为两大类:第一类为在同一平面内;第二类为空间几何体中的最短路线问题,对于平面内的最短路线问题可先画出方案图,然后确定最短距离及路径图。对于几何题内问题的关键是将立体图形转化为平面问题求解,然后构造直角三角形,利用勾股定理求解。
模型1.圆柱中的最短路径模型
【模型解读】圆柱体中最短路径基本模型如下:
计算跟圆柱有关的最短路径问题时,要注意圆柱的侧面展开图为矩形,利用两点之间线段最短结合勾股定理进行求解,注意展开后两个端点的位置,有时候需要用底面圆的周长进行计算,有时候需要用底面圆周长的一半进行计算。
注意:1)运用勾股定理计算最短路径时,按照展开—定点—连线—勾股定理的步骤进行计算;
2)缠绕类题型可以求出一圈的最短长度后乘以圈数。
【最值原理】两点之间线段最短。
例1.(2023·广东·八年级期中)如图,一个底面圆周长为24cm,高为9cm的圆柱体,一只蚂蚁从距离上边缘4cm的点A沿侧面爬行到相对的底面上的点B所经过的最短路线长为( )
A. B.15cm C.14cm D.13cm
【答案】D
【分析】将圆柱体展开,利用勾股定理进行求解即可.
【详解】解:将圆柱体的侧面展开,连接,如图所示:由于圆柱体的底面周长为24cm,
则, 又因为cm,所以(cm),
即蚂蚁沿表面从点A到点B所经过的最短路线长为13cm.故选:D.
【点睛】本题考查勾股定理的应用—最短路径问题.解题的关键是将立体图形展开为平面图形,利用勾股定理进行求解.
例2.(2023·重庆·八年级期末)如图,圆柱形玻璃杯高,底面周长为,在外侧距下底处有一只蜘蛛,与蜘蛛相对的圆柱形容器的上端距开口处的外侧点处有一只苍蝇,蜘蛛捕到苍蝇的最短路线长是______.
【答案】15
【分析】展开后连接,求出的长就是捕获苍蝇的蜘蛛所走的最短路径,过S作于E,求出、,根据勾股定理求出SF即可.
【详解】解:如图展开后连接,求出的长就是捕获苍蝇的蜘蛛所走的最短路径,
过S作于E,则(),(),
在中,由勾股定理得:(),故答案为15.
【点睛】本题考查勾股定理、平面展开-最短路线问题,关键是构造直角三角形,题目比较典型,难度适中.
例3.(2023春·山东济宁·八年级校考期中)春节期间,某广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为______米.
【答案】5
【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.
【详解】解:将圆柱表面切开展开呈长方形,则彩灯带长为2个长方形的对角线长,
圆柱高3米,底面周长2米,,,
每根柱子所用彩灯带的最短长度为.故答案为5.
【点睛】本题考查了平面展开最短路线问题,勾股定理的应用.圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
变式1.(2023·湖北十堰·统考一模)如图,这是一个供滑板爱好者使用的形池,该形池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是弧长为的半圆,其边缘(边缘的宽度忽略不计),点在上,一滑板爱好者从点滑到点,则他滑行的最短距离为( )
A. B. C. D.
【答案】C
【分析】滑行的距离最短,即是沿着的线段滑行,我们可将半圆展开为矩形来研究,展开后,、、三点构成直角三角形,为斜边,和为直角边,写出和的长,根据题意,由勾股定理即可得出的距离.
【详解】解:将半圆面展开可得:
米,米,
在中,(米).即滑行的最短距离为米.故选:C.
【点睛】本题考查了平面展开最短路径问题,型池的侧面展开图是一个矩形,此矩形的宽是半圆的弧长,矩形的长等于本题就是把型池的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
变式2.(2023春·四川德阳·八年级校考期中)如图,圆柱底面半径为,高为,点A,B分别是圆柱两底面圆周上的点,且A,B在同一条竖直直线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为___________cm.
【答案】15
【分析】要求圆柱体中两点之间的最短路径,最直接的作法,就是将圆柱体展开,然后利用两点之间线段最短解答.
【详解】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:;
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;∵圆柱底面半径为∴长方形的宽即是圆柱体的底面周长: ;
又∵圆柱高为,∴小长方形的一条边长是;
根据勾股定理求得;∴;故答案为:15.
【点睛】本题主要考查了平面展开--路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.
变式3.(2022·山东青岛·八年级期末)如图,一个圆桶,底面直径为16cm,高为18cm,则一只小虫从下底点A处爬到上底B处再回到A处,则小虫所爬的最短路径长是( )(取3)
A.60cm B.40cm C.30cm D.20cm
【答案】A
【分析】先将圆柱的侧面展开为一矩形,而矩形的长就是底面周长的一半,高就是圆柱的高,再根据勾股定理就可以求出其值.
【详解】解:展开圆柱的侧面如图,
根据两点之间线段最短就可以得知AB最短. 由题意,得AC=3×16÷2=24,
在Rt△ABC中,由勾股定理,得cm.
∵一只小虫从下底点A处爬到上底B处再回到A处,∴最短路径长为60cm.故选:A.
【点睛】本题考查了圆柱侧面展开图的运用,两点之间线段最短的运用,勾股定理的运用.在解答时将圆柱的侧面展开是关键.
模型2.长方体中的最短路径模型
【模型解读】长方体中最短路径基本模型如下:
计算跟长方体有关的最短路径问题时,要熟悉长方体的侧面展开图,利用两点之间线段最短结合勾股定理进行求解,注意长方体展开图的多种情况和分类讨论。
注意:1)长方体展开图分类讨论时可按照“前+右”、“前+上”和“左+上”三种情况进行讨论;
2)两个端点中有一个不在定点时讨论方法跟第一类相同。
【最值原理】两点之间线段最短。
例1.(2022·贵州贵阳·八年级校考阶段练习)如图所示,在正三棱柱中,已知,,一只蚂蚁从A点出发绕三棱柱侧面两圈到达点,则蚂蚁爬行的最短距离为( )
A. B. C. D.
【答案】D
【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将正三棱柱展开,然后利用两点之间线段最短解答.
【详解】∵一只蚂蚁从A点出发绕三棱柱侧面两圈到达点,
∴如图所示,将正三棱柱展开2次,∴,
∵正三棱柱的高∴.故选:D.
【点睛】此题考查了最短路径问题.解决本题的关键是熟练掌握用勾股定理的应用,要注意数形结合思想的应用.
例2.(2023·湖北十堰·统考二模)如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到处吃这块糖粒,已知盒子的长和宽为均为,高为,则蚂蚁爬行的最短距离为( ).
A.10 B.50 C.10 D.70
【答案】B
【分析】根据图形可知长方体的四个侧面都相等,所以分两种情况进行解答即可.
【详解】解:分两种情况:(其它情况与之重复)
①当蚂蚁从前面和右面爬过去时,如图1,连接,
在中,,,
根据勾股定理得:;
②当蚂蚁从前面和上面爬过去时,如图2,连接,
在中,,,
根据勾股定理得:;
蚂蚁爬行的最短距离为50.故选:B.
【点睛】本题考查了勾股定理的实际应用-求最短距离,读懂题意,熟悉立体图形的侧面展开图是解本题的关键.
例3.(2023·江苏南京·统考一模)如图,用7个棱长为1的正方体搭成一个几何体,沿着该几何体的表面从点M到点N的所有路径中,最短路径的长是( )
A.5 B. C. D.
【答案】A
【分析】先画出侧面展开图,根据两点之间践段最短,利用勾股定理求出线段的长即可.
【详解】将第一层小正方体的顶面和正面,以及第二层小正方体的顶面和正面展开,如下图,
连接,则最短路径,故选A
【点睛】本题主要考查了两点之间线段最短,以及勾股定理,正确画出侧面展开图,确定两点之间线段最短是解题的关键.
例4.(2023春·山西大同·八年级统考期中)如图,在墙角处放着一个长方体木柜(木柜与墙面和地面均没有缝腺),一只蚂蚁从柜角处沿着木柜表面爬到柜角处.若,,,则蚂蚁爬行的最短路程是( )
A. B. C. D.12
【答案】A
【分析】求出蚂蚁沿着木柜表面经线段到,以及蚂蚁沿着木柜表面经线段到的距离,再进行比较即可.
【详解】解:蚂蚁沿着木柜表面经线段到,爬过的路径的长是,
蚂蚁沿着木柜表面经线段到,爬过的路径的长是.
,最短路径的长是.故选A.
【点睛】此题主要考查了长方体展开图的对角线长度求法,这种题型经常在中考中出现,也是易错题型,希望能引起同学们的注意.
变式1.(2022秋·广东梅州·八年级校考阶段练习)如图,长方体的长、宽、高分别为 .如果一只小虫从点 开始爬行,经过两个侧面爬行到另一条侧棱的中点 处,那么这只小虫所爬行的最短路程为( )
A.5 B.4 C.6 D.7
【答案】A
【分析】根据题意把图形展开,连接,得出的长就是从处爬到处的最短路程,分为三种情况展开,根据勾股定理求出的长,再比较即可.
【详解】如图将正面与右面展开在同一平面,连接,由勾股定理得:,
如图将下底面与后面展开在同一平面,连接,由勾股定理得:,
如图将下底面与右面展开在同一平面,连接,由勾股定理得:,
∴从处爬到处的最短路程是,故选:.
【点睛】此题考查了立方体侧面展开图最短路径问题,解题关键是画出图形知道求出哪一条线段的长,题目具有一定的代表性,是一道比较好的题目,注意要进行分类讨论.
变式2.(2023春·八年级课时练习)棱长分别为两个正方体如图放置,点P在上,且,一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是______.
【答案】cm.
【分析】求出两种展开图的值,比较即可判断;
【详解】解:如图,有两种展开方法:
方法一∶,方法二∶.
故需要爬行的最短距离是cm.故答案为:cm.
【点睛】本题考查平面展开-最短问题,解题的关键是学会用转化的思想思考问题,属于中考常考题型.
变式3.(2023·浙江·八年级假期作业)小南同学报名参加了学校的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为________米.
【答案】
【分析】利用立体图形路径最小值为展开平面图的两点间距离,再根据勾股定理求解即可.
【详解】解:平面展开图为:
(米),故答案为.
【点睛】本题考查立体图形中两点间最短路径问题,通用办法是展开为平面图形,两点间最短路径为两点线段长度,利用水平距离和竖直距离得到直角三角形,勾股定理求出两点线段长度.熟悉立体图形中两点间最短路径问题的计算方法是解题的关键.
模型3.阶梯中的最短路径模型
【模型解读】阶梯中最短路径基本模型如下:
注意:展开—定点—连线—勾股定理
【最值原理】两点之间线段最短。
例1.(2023春·四川成都·九年级校考阶段练习)如图所示,是长方形地面,长,宽.中间竖有一堵砖墙高.一只蚂蚱从点爬到点,它必须翻过中间那堵墙,则它要走的路程s取值范围是________.
【答案】
【分析】连接,利用勾股定理求出的长,再把中间的墙平面展开,使原来的长方形长度增加而宽度不变,求出新长方形的对角线长即可得到范围.
【详解】解:如图所示,将图展开,图形长度增加,
原图长度增加,则,连接,
四边形是长方形,,宽,,
蚂蚱从点爬到点,它要走的路程.故答案为:.
【点睛】本题考查的是平面展开最短路线问题及勾股定理,根据题意画出图形是解答此题的关键.
例2.(2023春·重庆八年级课时练习)在一个长为 米, 宽为 米的长方形草地 上, 如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽,木块的主视图是边长为 米的正三角形, 一只蚂蚁从 点处到处需要走的最短路程是______米.
【答案】
【分析】如图,将木块展开,相当于长方形草地的长多了正三角形的一个边长,长方形的长为米,因为长方形的宽为3米,一只蚂蚁从点处到处需要走的最短路程是对角线,利用勾股定理求解即可.
【详解】解:如图,将木块展开,相当于长方形草地的长多了正三角形的一个边长,
长方形的长为米,
长方形的宽为3米,一只蚂蚁从点处到处需要走的最短路程是对角线,
米,故答案为.
【点睛】本题主要考查勾股定理的应用,根据题意将木块展开,再利用两点之间线段最短是解题关键.
变式1.(2023·陕西渭南·八年级统考期中)如图是一个二级台阶,每一级台阶的长、宽、高分别为、、.和是这个台阶两个相对的端点,在点有一只蚂蚁,想到点去受食,那么它爬行的最短路程是______.
【答案】
【分析】将台阶展开,得到一直角边长为,另一直角边为的直角三角形,求其斜边即可.
【详解】将台阶展开,得到一直角边长为,另一直角边为的直角三角形,
所以最短距离为,故答案为:.
【点睛】本题考查了几何体的展开图,勾股定理,熟练掌握展开图,勾股定理是解题的关键.
变式2.(2023秋·四川宜宾·八年级统考期末)如图是一个三级台阶,它的每一级的长、宽、高分别是4米、0.7米、0.3米,A、B是这个台阶上两个相对的顶点,A点处有一只蚂蚁,它想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是________米.
【答案】5
【分析】先将台阶展开,再根据勾股定理求解即可.
【详解】将三级台阶展开,如图所示.可知(米),(米),
根据两点之间线段最短,可知为最短路径,根据勾股定理得(米).
故答案为:5.
【点睛】本题考查了根据两点之间线段最短求最短路径,勾股定理等,勾股定理是求线段长的常用方法.
模型4.将军饮马与最短路径模型
【模型解读】将军饮马与最短路径基本模型如下:
解决线段之和最小值问题:对称+连线,根据两点之间线段最短解决。
注意:立体图形中从外侧到内侧最短路径问题需要先作对称,再运用两点之间线段最短的原理结合勾股定理求解。
【最值原理】两点之间线段最短。
例1.(2023·四川广安·统考中考真题)如图,圆柱形玻璃杯的杯高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿,且与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处所走的最短路程为___________.(杯壁厚度不计)
【答案】10
【分析】如图(见解析),将玻璃杯侧面展开,作关于的对称点,根据两点之间线段最短可知的长度即为所求,利用勾股定理求解即可得.
【详解】解:如图,将玻璃杯侧面展开,作关于的对称点,作,交延长线于点,连接,
由题意得:,,
∵底面周长为,,,
由两点之间线段最短可知,蚂蚁从外壁处到内壁处所走的最短路程为,故答案为:10.
【点睛】本题考查了平面展开——最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
例2.(2022·陕西·八年级期中)有一个如图所示的长方体透明玻璃水缸,高,水深,在水面线上紧贴内壁处有一粒食物,且,一只小虫想从水缸外的处沿水缸壁爬到水缸内的处吃掉食物.(1)你认为小虫应该沿怎样的路线爬行才能使爬行的路线最短,请你画出它爬行的最短路线,并用箭头标注.(2)求小虫爬行的最短路线长(不计缸壁厚度).
【答案】(1)见解析;(2)100cm
【分析】(1)做出A关于BC的对称点A’,连接A’G,与BC交于点Q,由两点之间线段最短,此时A’G最短,即AQ+QG最短;(2)A’G为直角△A’EG的斜边,根据勾股定理求解即可.
【详解】解:(1)如下图所示,
作点A关于BC所在直线的对称点,连接,与交于点,
由两点之间线段最短,此时A’G最短,则为最短路线.
(2)∵,∴,∴.
在中,,,∴.
由对称性可知,∴.故小虫爬行的最短路线长为100cm.
【点睛】本题考查的是利用勾股定理求最短路径问题,本题的关键是根据对称性作出A的对称点A’,再根据两点之间线段最短,从而可找到路径求出解.
例3.(2023春·河北保定·八年级统考期中)如图,高速公路的同一侧有A,B两城镇,它们到高速公路所在直线的距离分别为,,.要在高速公路上C,D之间建一个出口P,使A,B两城镇到P的距离之和最小,则这个最短距离为( )
A. B. C. D.
【答案】B
【分析】根据题意画出图形,再利用轴对称求最短路径的方法得出点位置,进而结合勾股定理得出即可.
【详解】解:如图所示:作点关于直线的对称点,再连接,交直线于点
则此时最小,过点作延长线于点,
,,,,则,
在中,,则的最小值为:.故选:B.
【点睛】此题主要考查了应用与设计作图,两点之间线段最短、勾股定理等知识,解题的关键是学会利用对称解决最短问题.
变式1.(2023春·湖北武汉·八年级校考阶段练习)如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿且与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为( ).(杯壁厚度不计)
A.20 B.25 C.30 D.40
【答案】B
【分析】化曲为直,利用勾股定理解决.
【详解】把玻璃杯的侧面展开,如图,把点A向上平移6cm到点C,连接,过点B作于D,由已知得:,,,
在中,由勾股定理得:,
则蚂蚁从外壁A处到内壁B处的最短距离为.故选:B
【点睛】本题考查了勾股定理的应用,根据题意把圆柱展开,化曲为直是解决问题的关键.
变式2.(2022·山东菏泽·八年级阶段练习)如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为的半圆,其边缘.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )m.(取3)
A.30 B.28 C.25 D.22
【答案】C
【分析】根据题意画出侧面展开图,作点C关于AB的对称点F,连接DF,根据半圆的周长求得,根据对称求得,在Rt△CDF中,勾股定理求得.
【详解】其侧面展开图如图:作点C关于AB的对称点F,连接DF,
∵中间可供滑行的部分的截面是半径为2.5cm的半圆,
∴BC=πR=2.5π=7.5cm,AB=CD=20cm,∴CF=2BC=15cm,
在Rt△CDF中,DF=cm,故他滑行的最短距离约为cm.故选C.
【点睛】本题考查了勾股定理最短路径问题,作出侧面展开图是解题的关键.
变式3.(2023春·广东八年级课时练习)如图,A,B两个村庄在河CD的同侧,两村庄的距离为a千米,,它们到河CD的距离分别是1千米和3千米.为了解决这两个村庄的饮水问题,乡政府决定在河CD边上修建一水厂向A,B两村输送水.(1)在图上作出向A,B两村铺设水管所用材料最省时的水厂位置M.(只需作图,不需要证明)。(2)经预算,修建水厂需20万元,铺设水管的所有费用平均每千米为3万元,其他费用需5万元,求完成这项工程乡政府投入的资金至少为多少万元.
【答案】(1)见解析;(2)50万元.
【分析】(1)作点A关于直线的对称点,连接,交于M点,即M为所求;
(2)连接交于H点,过点B作,根据勾股定理求出,即可得出答案.
【详解】(1)解:如图,作点A关于直线的对称点,连接,交于M点,即M为所求.
(2)解:如图,连接交于H点,过点B作,
由题意可知:,,,
∴,
∴在中,,
∴在中,,
由对称性质可知:,水管长,
完成这项工程乡政府投入的资金至少为(万元)
【点睛】本题考查了轴对称最短路线问题,勾股定理,题目比较典型,是一道比较好的题目,考查了学生的动手操作能力和计算能力.
课后专项训练
1.(2022·浙江金华初三月考)如图,圆柱底面半径为cm,高为18cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A.24cm B.30cm C.2cm D.4cm
【答案】B
【分析】要求圆柱体中两点之间的最短路径,最直接的作法,就是将圆柱体展开,然后利用两点之间线段最短解答.
【解析】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;∵圆柱底面半径为cm,∴长方形的宽即是圆柱体的底面周长:2π×=8cm;
又∵圆柱高为18cm,∴小长方形的一条边长是6cm;
根据勾股定理求得AC=CD=DB=10cm;∴AC+CD+DB=30cm;故选:B.
【点睛】本题主要考查了圆柱的计算、平面展开 路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.
2.(2022·重庆八年级期中)如图,长方体的底面边长是1cm和3cm,高是6cm,如果用一根细线从点开始经过个侧面缠绕一圈到达,那么用细线最短需要( )
A.12cm B.10cm C.13cm D.11cm
【答案】B
【分析】要求所用细线的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”,利用勾股定理求出所需结果.
【详解】解:如图,将长方体展开,连接A、B′,则AA′=1+3+1+3=8(cm), A′B′=6cm,
根据两点之间线段最短,由勾股定理得:AB′2=AA′2+A′B′2=82+62=102cm,所以AB′=10 cm.故选:B.
【点睛】本题考查了平面展开 最短路径问题,本题的关键是把长方体的侧面展开“化立体为平面”,构造直角三角形运用勾股定理解决.
3.(2022·山西八年级期末)如图所示,是长方形地面,长,宽,中间整有一堵砖墙高,一只蚂蚁从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A.20 B.24 C.25 D.26
【答案】D
【分析】将题中图案展开后,连接AC,利用勾股定理可得AC长,将中间的墙展开在平面上,则原矩形长度增加宽度不变,求出新矩形的对角线长即为所求.
【详解】解:展开如图得新矩形,连接AC,则其长度至少增加2MN,宽度不变,
由此可得:,
根据勾股定理有:故选D.
【点睛】本题考查平面展开图形最短路线问题以及勾股定理得应用;解题关键在于根据题意画出正确的平面展开图.
4.(2022·重庆初二月考)圆柱形杯子的高为18cm,底面周长为24cm,已知蚂蚁在外壁A处(距杯子上沿2cm)发现一滴蜂蜜在杯子内(距杯子下沿4cm),则蚂蚁从A处爬到B处的最短距离为( )
A. B.28 C.20 D.
【答案】C
分析:将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
【解析】如图所示,将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B= (cm)故选C.
点睛:本题考查了勾股定理、最短路径等知识.将圆柱侧面展开,化曲面为平面并作出A关于EF的对称点A′是解题的关键.
5.(2023·广东惠州·八年级阶段练习)如图,是一块长、宽、高分别是、和的长方体木块,一只蚂蚁要从顶点出发,沿长方体的表面爬到和相对的顶点处吃食物,则它需要爬行的最短路线长是( ).
A. B.6 C. D.
【答案】A
【分析】根据长方体的侧面展开计算:沿前表面和上表面所构成矩形的对角线爬行距离,沿前表面和右表面所构成矩形的对角线爬行距离,沿左表面和上表面所构成矩形的对角线爬行距离,沿左表面和后表面所构成矩形的对角线爬行距离,再比较大小即可;
【详解】解:如图1,当蚂蚁由点经前表面和上表面所构成矩形的对角线到达点时,
由勾股定理可得,
如图2,当蚂蚁由点经前表面和右表面所构成矩形的对角线到达点时,
由勾股定理可得,
如图3,当蚂蚁由点经左表面和上表面所构成矩形的对角线到达点时,
由勾股定理可得,
如图4,当蚂蚁由点经左表面和后表面所构成矩形的对角线到达点时,
由勾股定理可得,∵,故选: A.
【点睛】本题考查了长方体的侧面展开,两点间的最短距离,勾股定理;根据长方体的侧面展开分类讨论是解题关键.
6.(2023春·安徽·八年级期中)如图,圆柱形容器高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( )
A. B. C. D.
【答案】C
【分析】将圆柱侧面展开,如图所示,作出A点关于的对称点,连接,根据两点之间线段最短,可知即为最短距离,然后根据勾股定理求解.
【详解】解:将圆柱侧面展开,如图所示,作出A点关于的对称点,过点B作于点C,
∵形容器高为,点A处离杯上沿,点B处离杯底,
∴,,∴,
∵底面周长为,∴,
根据勾股定理可得:,故选:C.
【点睛】本题考查平面展开,最短路径问题,将图形展开,利用轴对称的性质找出最短路径是解题的关键.
7.(2023秋·河南郑州·八年级校考期末)如图,一大楼的外墙面与地面垂直,点P在墙面上,若米,点P到的距离是8米,有一只蚂蚁要从点P爬到点B,它的最短行程是( )米.
A. B. C. D.
【答案】D
【分析】可将教室的墙面与地面展开,连接,根据两点之间线段最短,利用勾股定理求解即可.
【详解】解:如图,过P作于G,连接,
(米),(米),(米),
(米),(米)
这只蚂蚁的最短行程应该是米,故选:D.
【点睛】本题主要考查了平面展开-最短路径问题,解题关键是立体图形中的最短距离,通常要转换为平面图形的两点间的线段长来进行解决.
8.(2022秋·广东茂名·八年级校考期中)固定在地面上的一个正方体木块(如图①),其棱长为,沿其相邻三个面的对角线(图中虚线)去掉一角,得到如图②所示的几何体木块,一只蚂蚁沿着该木块的表面从点A爬行到点B的最短路程为( )
A. B. C. D.
【答案】A
【分析】根据两点之间线段最短,将图②展开,利用勾股定理进行求解即可.
【详解】解:如图,正方体上表面的对角线为,将图②展开,连接交于点,线段的长度即为蚂蚁爬行的最短路程,
由题意可知:为等边三角形,为等腰直角三角形,
∵,∴,∴,∴,
∵正方体的棱长为,∴,,
在中,,在中,,
∴;故选A.
【点睛】本题考查勾股定理的应用.解题关键是将立体图像展开,根据两点之间线段最短,确定最短路径.
9.(2023·全国·八年级假期作业)如图是一个长方体盒子,其长、宽、高分别为4,2,9,用一根细线绕侧面绑在点A,B处,不计线头,细线的最短长度为( )
A.12 B.15 C.18 D.21
【答案】B
【分析】把长方体沿边剪开,再根据勾股定理计算即可.
【详解】如图所示,连接,则即为所求的最短长度,,
在中,故选:B.
【点睛】本题主要考查了勾股定理的应用,把长方体沿边剪开得到矩形是解题的关键.
10.(2023春·成都市八年级课时练习)如图,在长方体盒子中,已知,长为的细直木棒恰好从小孔G处插入,木棒的一端I与底面接触,当木棒的端点I在长方形内及边界运动时,长度的最小值为( )
A. B. C. D.
【答案】A
【分析】当最大时,最小,当I运动到点A时,最大,根据勾股定理求解即可.
【详解】解:当最大时,最小,当I运动到点A时,最大,
此时,而,
∴,∴长度的最小值为.故选:A.
【点睛】本题考查了勾股定理的应用,根据勾股定理求出的最大值是解题的关键.
11.(2022·陕西八年级期末)如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点处吃食物,那么它爬行的最短路程是___________.
【答案】5
【分析】利用平面展开图有3种情况,画出图形利用勾股定理求出MN的长即可.
【详解】解:分三种情况:如图1,,
如图2,,∴AP=5, 如图3,,
, 它爬行的最短路程为5,故答案为:5.
,
【点睛】此题考查平面展开图最短路径问题和勾股定理应用,利用展开图有3种情况分析得出是解题关键.
12.(2021·重庆八年级期末)如图,三级台阶,每一级的长、宽、高分别为8dm、3dm、,A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为______dm.
【答案】17
【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.
【详解】解:三级台阶平面展开图为长方形,长为8dm,宽为,
则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.可设蚂蚁沿台阶面爬行到B点最短路程为xdm,
由勾股定理得:,解得.故答案为:17.
【点睛】本题考查了平面展开最短路径问题,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.
13.(2022·吉林长春·八年级期末)如图,有一个圆柱,底面圆的直径AB=cm,高BC=10cm,在BC的中点P处有一块蜂蜜,聪明的蚂蚁能够找到距离食物的最短路径,则蚂蚁从点A爬到点P的最短路程为 _____cm.
【答案】13
【分析】化“曲”为“平”,在平面内,得到两点的位置,再根据两点之间线段最短和勾股定理求解即可.
【详解】将圆柱体的侧面展开,如图所示:
AB=底面周长=××=12(cm),BP=BC=5(cm),所以AP=(cm),
故蚂蚁从A点爬到P点的最短距离为13cm,故答案为:13.
【点睛】本题考查最短距离问题,化“曲”为“平”,在平面内,利用两点之间线段最短和勾股定理是常用求解方法.
14.(2023春·安徽合肥·八年级校考期中)如图,正方体盒子的棱长为,O为的中点,现有一只蚂蚁位于点C处,它想沿正方体的表面爬行到点O处获取食物,则蚂蚁需爬行的最短路程为_______.
【答案】
【分析】根据两点之间线段最短,用勾股定理求解.
【详解】解:如图,连接,则线段的长就是蚂蚁需爬行的最短路程,
∵正方体的棱长为,O为的中点,∴,,,
由勾股定理得,
答:蚂蚁需爬行的最短路程为,故答案为:.
【点睛】本题考查两点之间线段最短,灵活运用所学知识是关键.
15.(2023春·安徽合肥·八年级合肥寿春中学校考期中)如图,一个圆柱形食品盒,它的高为,底面圆的周长为
(1)点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物,则蚂蚁需要爬行的最短路程是______;
(2)将左图改为一个无盖的圆柱形食品盒,点C距离下底面,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如右图),则蚂蚁爬行的最短路程是___.
【答案】
【分析】(1)把圆柱侧面展开,在中,利用勾股定理求解即可.
(2)将圆柱侧面展开,得到矩形,作点关于的对称点,构造,根据勾股定理求出即可解决问题.
【详解】(1)如图,把圆柱侧面展开,在中,
∵,∴ ,故答案为:.
(2)如图所示,点与点关于对称,可得,,
则最短路程为故答案为:.
【点睛】本题考查了勾股定理求线段最短距离,轴对称的性质,熟练掌握勾股定理是解题的关键.
16.(2023秋·四川成都·八年级统考期末)小强家因装修准备用电梯搬运一些木条上楼,如图,已知电梯的长、宽、高分别是,,,那么电梯内能放入这些木条的最大长度是 ______
【答案】
【分析】由勾股定理求出,再由勾股定理求出即可.
【详解】如图所示:
由勾股定理知:,,
即电梯内能放入这些木条的最大长度是.故答案为:.
【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理,并能进行推理计算是解决问题的关键.
17.(2023·湖南永州·八年级校考阶段练习)如图是长、宽、高的长方体容器.
(1)求底面矩形的对角线的长;(2)长方体容器内可完全放入的棍子最长是多少?
(3)一只蚂蚁从D点爬到E点最短路径是多少?
【答案】(1)底面矩形的对角线的长为(2)长方体容器内可完全放入的棍子最长是
(3)蚂蚁从D点爬到E点最短路径
【分析】(1)根据题意运用勾股定理即可得出结果;(2)根据题意连接、,两次运用勾股定理即可得出结果;(3)分别求出三种情况下蚂蚁爬行的最短距离,然后进行比较,得出蚂蚁爬行的最短距离即可.
【详解】(1)解:∵、,,∴对角线的长为:;
答:底面矩形的对角线的长为.
(2)解:连接、,如图所示:
在中,∵、,,∴,
在中, .答:这个盒子最长能放的棍子.
(3)解:将前面的面和右边的面展开,如图所示:
此时蚂蚁从D点爬到E点最短路径为:;
将前面的面和上边的面展开,如图所示:
此时蚂蚁从D点爬到E点最短路径为:;
将左边的面和上边的面展开,如图所示:
此时蚂蚁从D点爬到E点最短路径为:;
∵,∴蚂蚁从D点爬到E点最短路径.
【点睛】本题考查的是勾股定理的应用,根据题意,作出辅助线、构造出直角三角形是解答此题的关键.
18.(2022秋·广东佛山·八年级统考期末)初中几何的学习始于空间的“实物和具体模型”,聚焦平面的“几何图形的特征和运用”,形成了空间几何问题要转化为平面几何问题的解题策略.
问题提出:如图所示是放在桌面上的一个圆柱体,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,如何求最短路程呢?(1)问题分析:蚂蚁从点出发沿着圆柱体的表面爬行到点,可以有几条路径?在图中画出来;(2)问题探究:①若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;②若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;③若圆柱体的底面圆的半径为,高为,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程.
【答案】(1)3条,图形见解析 (2)①;②;③
【分析】(1)共有3条路径,第一条先沿圆柱体的高爬行,再从上底面边缘爬行;第二条先沿圆柱体的高爬行,再从上底面直径爬行;第三条沿圆柱体侧面爬行,即可;
(2)①连接,利用两点之间,线段最短,在中,根据勾股定理,求出的长,即可求解;②利用两点之间,线段最短,在中,根据勾股定理,求出的长,即可求解;③利用两点之间,线段最短,在中,根据勾股定理,求出的长,即可求解.
【详解】(1)解:共有3条路径,如下图:
(2)解:①如图,连接,根据题意得:,,∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为;
②如图,连接, 根据题意得:,,∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为;
③如图,连接, 根据题意得:,,∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为.
【点睛】本题主要考查了勾股定理的实际应用,熟练掌握勾股定理是解题的关键.
19.(2022秋·广东深圳·八年级统考期末)如图,一个无盖长方体的小杯子放置在桌面上,,;
(1)一只蚂蚁从点出发,沿小杯子外表面爬到点,求蚂蚁怎样走最短,最短路程是多少?
(2)为了怕杯子落入灰尘又方便使用,现在需要给杯子盖上盖子,并把一双筷子放进杯子里,请问,筷子的最大长度是多少?
【答案】(1)如方法一的路线最短,最短路线为(2)筷子的最大长度是
【分析】(1)分别讨论将面和面展开,将面和上底面展开两种情况,再利用勾股定理计算,进而比较即可求解;
(2)当筷子沿倾斜放的时候,能够放的最长,利用勾股定理计算即可.
【详解】(1)方法一:将面和面展开,如图,
∵,,∴,
由勾股定理得;
方法二:将面和上底面展开,如图,
∵,,∴,
由勾股定理得;
所以,如方法一的路线最短,最短路线为;
(2)如图,当筷子沿倾斜放的时候,能够放的最长,
∵,,∴由勾股定理得,
∴,所以,筷子的最大长度是.
【点睛】本题考查了勾股定理的应用,准确理解题意,熟练掌握勾股定理是解题的关键.
20.(2023春·全国·八年级专题练习)我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点处缠绕而上.
(1)若绕五周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
(2)若绕周后其末端恰好到达点处,则问题中葛藤的最短长度是________尺.
【答案】(1)25(2)
【分析】(1)根据题意画出图形,在Rt中,再根据勾股定理求解即可;
(2)在Rt中根据勾股定理求解即可.
【详解】(1)解:如图所示,
在Rt中,,,(尺)
答:葛藤长为25尺.故答案为:25;
(2)解:在Rt中,,,
(尺),
答:葛藤长为尺.故答案为:.
【点睛】本题考查的是平面展开—最短路径问题,能够根据题意画出图形,构造出直角三角形是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
