1.2 锐角三角函数的计算 (1) 课件(共15张PPT)
文档属性
| 名称 | 1.2 锐角三角函数的计算 (1) 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-11 21:19:27 | ||
图片预览




文档简介
(共15张PPT)
浙教版九年级下册
1.2 锐角三角函数的计算 (1)
第一章 解直角三角形
.
.
.
.
.
.
.
1
.
.
.
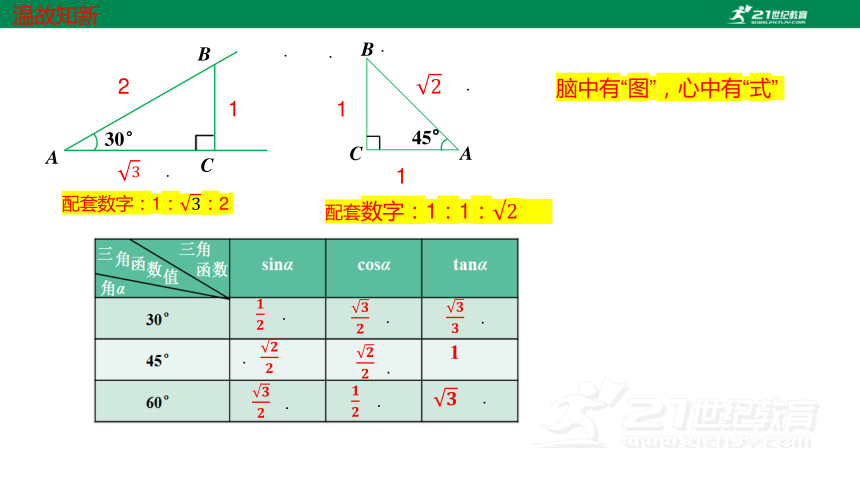
A
B
C
30°
配套数字:1::2
1
.
2
45°
A
B
C
配套数字:1:1:
1
1
.
.
脑中有“图”,心中有“式”
温故知新
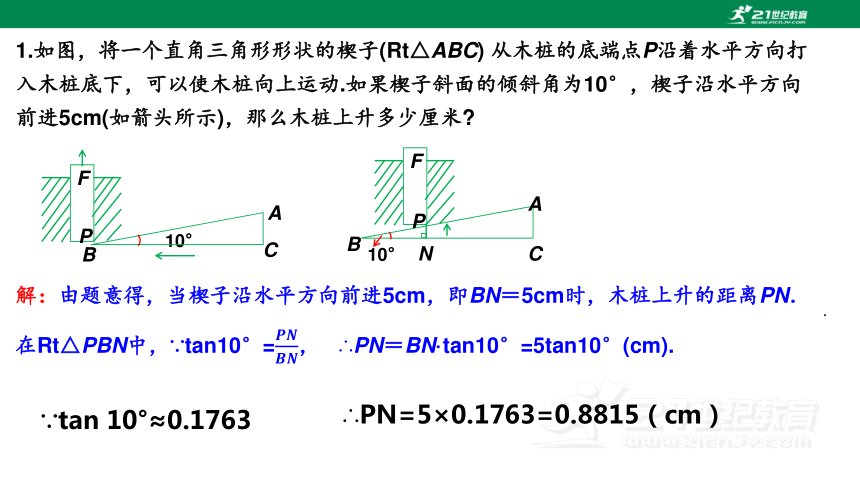
1.如图,将一个直角三角形形状的楔子(Rt△ABC) 从木桩的底端点P沿着水平方向打入木桩底下,可以使木桩向上运动.如果楔子斜面的倾斜角为10°,楔子沿水平方向前进5cm(如箭头所示),那么木桩上升多少厘米
10°
F
P
A
B
C
10°
F
P
A
B
C
N
解:由题意得,当楔子沿水平方向前进5cm,即BN=5cm时,木桩上升的距离PN.
在Rt△PBN中,∵tan10°=, ∴PN=BN·tan10°=5tan10°(cm).
.
∵tan 10°≈0.1763
∴PN=5×0.1763=0.8815(cm)
2.求下列三角函数值(精确到0.0001):
cos 70°,sin 29.12°,
cos 37°42'6", tan 18°31'.
解: cos 70°=0.3420,
sin 29.12°=0.4866,
cos 37°42'6"=0.7912,
tan 18°31'=0.3349.
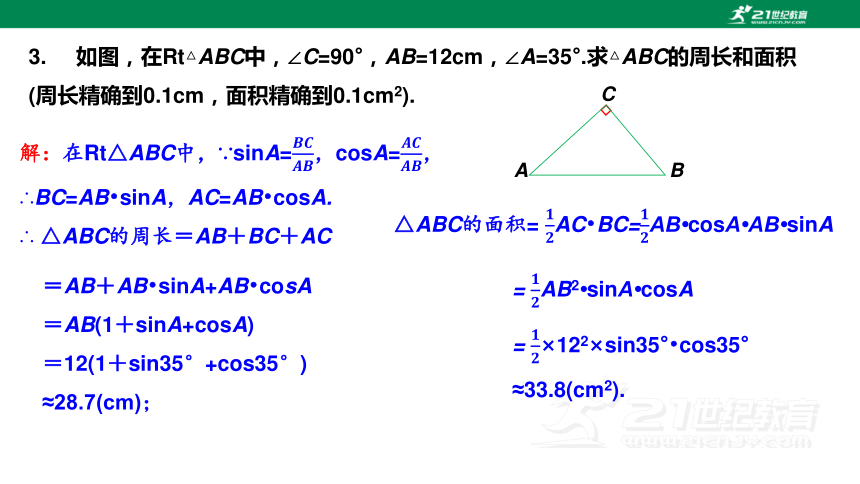
3. 如图,在Rt△ABC中,∠C=90°,AB=12cm,∠A=35°.求△ABC的周长和面积(周长精确到0.1cm,面积精确到0.1cm2).
解:在Rt△ABC中,∵sinA=,cosA=,
∴BC=AB sinA,AC=AB cosA.
∴ △ABC的周长=AB+BC+AC
C
A
B
=AB+AB sinA+AB cosA
=AB(1+sinA+cosA)
=12(1+sin35°+cos35°)
≈28.7(cm);
△ABC的面积= AC BC=AB cosA AB sinA
= AB2 sinA cosA
= ×122×sin35° cos35°
≈33.8(cm2).
1、用计算器求:sin30°= ;sin40°= ;
sin60°= ;sin80°= ;
由此,可用不等号连接:
sin30° sin40° sin60° sin80°.
夯实基础,稳扎稳打
0.5000
0.6428
0.8660
0.9848
<
<
<
当锐角α逐渐增大时,它的正弦值逐渐增大.
由此,可用不等号连接:
cos15° cos30° cos60° cos75°.
2、用计算器求:cos15°= ;cos30°= ;cos60°= ;cos75°= ;
0.9659
0.866
0.5000
0.2588
>
当锐角α逐渐增大时,它的余弦值逐渐减小.
>
>
6.如图,河两岸AB、CD互相平行,小明和小慧要测量河的宽度,小明在A点测得
对岸河边的树G正好在他的正北方向,小慧站在小明正东方向的B点,测得∠ABG=700,
A、B两点之间的距离是5m.根据上述测量数据,你能求出河的宽度吗?
有弦用弦,无弦用切
5tan700
700
5m
∟
4.如图所示,小芳在中心广场放风筝,已知风筝拉线长50米(假设拉线是直的),且拉线与水平地面的夹角为50°,若小芳的身高忽略不计,则风筝离水平地面的高度是多少米?(结果精确到0.1).
解:如图,作AC⊥OB于点C,
∵AO=50米,∠AOC=50°,
∴AC=OA·sin50°=50×0.766=38.3(米).
50m
∟
50sin500
有弦用弦,无弦用切
5.锐角的正弦值随着锐角的确定而确定,变化而变化,请画图直观表示变化规律
x
y
0
半径为1的圆
当锐角α逐渐增大时,它的正弦值逐渐增大.
当 00<α<β<900时,0思维拓展,更上一层
6.锐角的余弦值随着锐角的确定而确定,变化而变化,请画图直观表示变化规律
x
y
0
半径为1的圆
当锐角α逐渐增大时,它的余弦值逐渐减小.
7.锐角的正弦值随着锐角的确定而确定,变化而变化,请画图直观表示变化规律
x
y
0
半径为1的圆
当锐角α逐渐增大时,它的正切值逐渐增大.
半径为1的圆
8.探索下列关系式是否成立(00<α<900)
(1) sinα+cosα
x
y
0
(2) sin2α=2sinα
x
y
0
×
×
cosα
sinα
1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级下册
1.2 锐角三角函数的计算 (1)
第一章 解直角三角形
.
.
.
.
.
.
.
1
.
.
.
A
B
C
30°
配套数字:1::2
1
.
2
45°
A
B
C
配套数字:1:1:
1
1
.
.
脑中有“图”,心中有“式”
温故知新
1.如图,将一个直角三角形形状的楔子(Rt△ABC) 从木桩的底端点P沿着水平方向打入木桩底下,可以使木桩向上运动.如果楔子斜面的倾斜角为10°,楔子沿水平方向前进5cm(如箭头所示),那么木桩上升多少厘米
10°
F
P
A
B
C
10°
F
P
A
B
C
N
解:由题意得,当楔子沿水平方向前进5cm,即BN=5cm时,木桩上升的距离PN.
在Rt△PBN中,∵tan10°=, ∴PN=BN·tan10°=5tan10°(cm).
.
∵tan 10°≈0.1763
∴PN=5×0.1763=0.8815(cm)
2.求下列三角函数值(精确到0.0001):
cos 70°,sin 29.12°,
cos 37°42'6", tan 18°31'.
解: cos 70°=0.3420,
sin 29.12°=0.4866,
cos 37°42'6"=0.7912,
tan 18°31'=0.3349.
3. 如图,在Rt△ABC中,∠C=90°,AB=12cm,∠A=35°.求△ABC的周长和面积(周长精确到0.1cm,面积精确到0.1cm2).
解:在Rt△ABC中,∵sinA=,cosA=,
∴BC=AB sinA,AC=AB cosA.
∴ △ABC的周长=AB+BC+AC
C
A
B
=AB+AB sinA+AB cosA
=AB(1+sinA+cosA)
=12(1+sin35°+cos35°)
≈28.7(cm);
△ABC的面积= AC BC=AB cosA AB sinA
= AB2 sinA cosA
= ×122×sin35° cos35°
≈33.8(cm2).
1、用计算器求:sin30°= ;sin40°= ;
sin60°= ;sin80°= ;
由此,可用不等号连接:
sin30° sin40° sin60° sin80°.
夯实基础,稳扎稳打
0.5000
0.6428
0.8660
0.9848
<
<
<
当锐角α逐渐增大时,它的正弦值逐渐增大.
由此,可用不等号连接:
cos15° cos30° cos60° cos75°.
2、用计算器求:cos15°= ;cos30°= ;cos60°= ;cos75°= ;
0.9659
0.866
0.5000
0.2588
>
当锐角α逐渐增大时,它的余弦值逐渐减小.
>
>
6.如图,河两岸AB、CD互相平行,小明和小慧要测量河的宽度,小明在A点测得
对岸河边的树G正好在他的正北方向,小慧站在小明正东方向的B点,测得∠ABG=700,
A、B两点之间的距离是5m.根据上述测量数据,你能求出河的宽度吗?
有弦用弦,无弦用切
5tan700
700
5m
∟
4.如图所示,小芳在中心广场放风筝,已知风筝拉线长50米(假设拉线是直的),且拉线与水平地面的夹角为50°,若小芳的身高忽略不计,则风筝离水平地面的高度是多少米?(结果精确到0.1).
解:如图,作AC⊥OB于点C,
∵AO=50米,∠AOC=50°,
∴AC=OA·sin50°=50×0.766=38.3(米).
50m
∟
50sin500
有弦用弦,无弦用切
5.锐角的正弦值随着锐角的确定而确定,变化而变化,请画图直观表示变化规律
x
y
0
半径为1的圆
当锐角α逐渐增大时,它的正弦值逐渐增大.
当 00<α<β<900时,0
6.锐角的余弦值随着锐角的确定而确定,变化而变化,请画图直观表示变化规律
x
y
0
半径为1的圆
当锐角α逐渐增大时,它的余弦值逐渐减小.
7.锐角的正弦值随着锐角的确定而确定,变化而变化,请画图直观表示变化规律
x
y
0
半径为1的圆
当锐角α逐渐增大时,它的正切值逐渐增大.
半径为1的圆
8.探索下列关系式是否成立(00<α<900)
(1) sinα+cosα
x
y
0
(2) sin2α=2sinα
x
y
0
×
×
cosα
sinα
1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
