6.1 矩形（第一课时）

(共14张PPT)
横山中学
方永鑫
矩 形
创设情境，引出课题
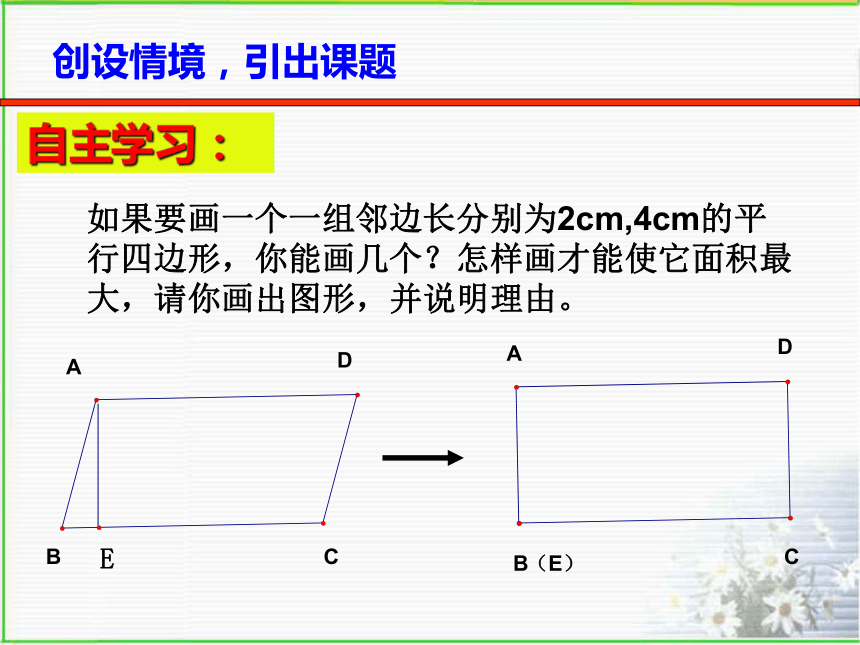
如果要画一个一组邻边长分别为2cm,4cm的平
行四边形，你能画几个？怎样画才能使它面积最大，请你画出图形，并说明理由。
自主学习：
A
B
C
D
E
A
B
C
D
（E）
矩形：
有一个角是直角的平行四边形
特殊性
小学里学过的长方形、正方形都是矩形
矩形：
想一想：你能举出在人们的日常生活和
生产实践中，有哪些东西是矩形的？
探索性质，尝试证明
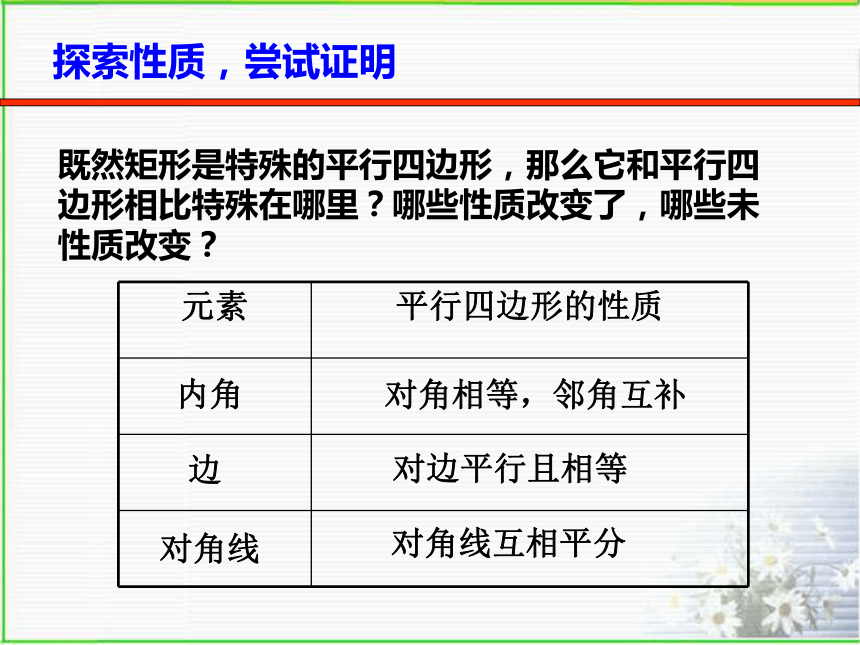
既然矩形是特殊的平行四边形，那么它和平行四
边形相比特殊在哪里？哪些性质改变了，哪些未
性质改变？
元素 平行四边形的性质
内角
边
对角线
对角相等，邻角互补
对边平行且相等
对角线互相平分
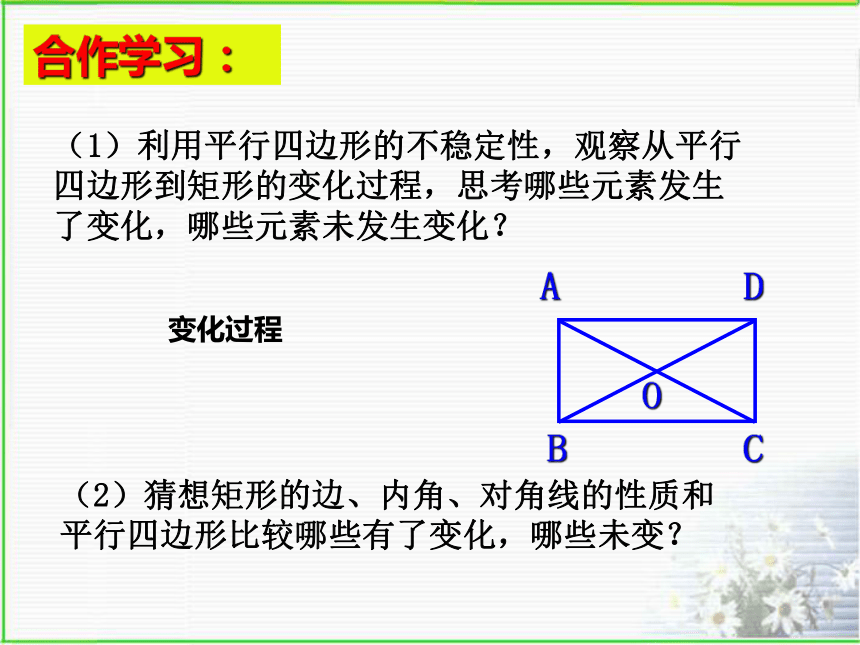
合作学习：
（1）利用平行四边形的不稳定性，观察从平行
四边形到矩形的变化过程，思考哪些元素发生
了变化，哪些元素未发生变化？
O
A
B
C
D
（2）猜想矩形的边、内角、对角线的性质和
平行四边形比较哪些有了变化，哪些未变？
变化过程
元素 平行四边形的性质 矩形的性质
内角 对角相等，邻角互补
边 对边平行且相等
对角线 对角线互相平分
四个角都是直
角
对边平行且相
等
对角线互相平
分且相等
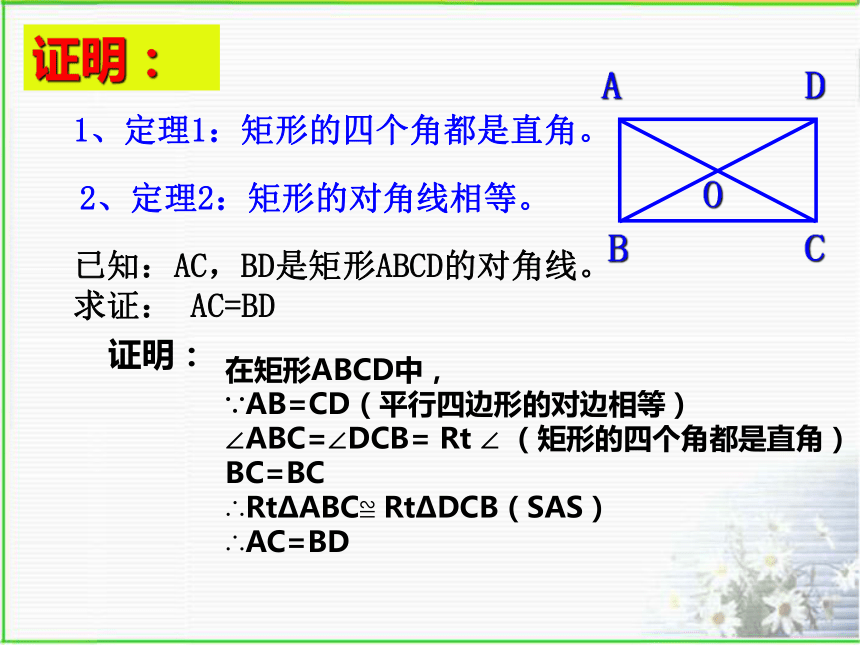
证明：
1、定理1：矩形的四个角都是直角。
2、定理2：矩形的对角线相等。
已知：AC，BD是矩形ABCD的对角线。
求证： AC=BD
O
A
B
C
D
证明：
在矩形ABCD中，
∵AB=CD（平行四边形的对边相等）
∠ABC=∠DCB= Rt ∠ （矩形的四个角都是直角）
BC=BC
∴RtΔABC≌ RtΔDCB（SAS）
∴AC=BD
运用性质，提高能力
问题1：（1）根据矩形的上述性质，
你能发现OA、OB、OC、OD有什么
关系？
（2）由OA=OB=OC=OD可知图中有几
个等腰三角形？这些三角形全等吗
面积相等吗？
O
A
B
C
D
（3）若已知BC=8，O到BC的距离为3，求矩形的
面积，周长，对角线的长度。
（3）若∠AOD=120度，AB=4厘米，求矩形的对
角线长，周长，面积。
问题2：如图，矩形ABCD的两条对
角线相交于点O
O
A
B
C
D
（1）若∠AOD=120度，试判断
ΔAOB的形状。
（2）若要得到ΔAOB是等边Δ，你可以添加一
个什么条件？
矩形的对称性：
任意画一个矩形，请探求它的对称性，如果是中心
对称图形，找出它的对称中心，如果是轴对称图形
找出它的对称轴。
O
举例：是轴对称图形的有哪些，是中心对称图形的有哪
些，既是轴对称图形又是中心对称图形的有哪些？
既是轴对称图形又是中心对称图形
中心对称
收获
练习：
1、已知矩形的周长是14cm,相邻两边的差
是1cm, 那么这个矩形的面积是多少？
2、如图，在矩形ABCD中，对角线AC，BD相交
于点O，已知AB=2cm,AC=6cm,则BC= ？cm,
ΔBOC 的周长=？ cm.
O
A
B
C
D
收获
收获：
通过本节课的学习，
你有哪些收获拿出来
和大家分享吧！
送给大家的祝福:
忧愁是可减的！
快乐是可加的！
在未来趋于正无穷大的日子里，
幸福是连续的！
对你的祝福是正数的绝对值，
它一定是大于零的！
祝你每天的快乐和幸福是连续
上升的折线统计图
欢迎您来横山中学指导交流！
谢谢！
2007.4.13
作业：
3、如图，在矩形ABCD中，M为BC的中点
求证：AM=DM
M
A
B
C
D