2023浙教版数学八年级下册第五章综合素质评价(含答案)
文档属性
| 名称 | 2023浙教版数学八年级下册第五章综合素质评价(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 889.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 16:51:08 | ||
图片预览



文档简介
第五章综合素质评价
一、选择题(本题有10小题,每小题3分,共30分)
1. [2023·台州临海市期中]如图,在矩形ABCD中,对角线AC,BD交于点O,如果∠ADB=32°,那么∠AOB的度数为( )
A. 32° B. 48° C. 64° D. 96°
INCLUDEPICTURE"卷8ZJ+37.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+37.EPS" \* MERGEFORMATINET (第1题) INCLUDEPICTURE"卷8ZJ+38.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+38.EPS" \* MERGEFORMATINET (第3题)
2. 菱形、矩形、正方形都具有的性质是( )
A. 四条边相等,四个角相等 B. 对角线相等
C. 对角线互相垂直 D. 对角线互相平分
3. 如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB的度数是( )
A. 20° B. 30° C. 50° D. 22. 5°
4. 如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A. 当AB=BC时,它是正方形 B. 当AC⊥BD时,它是菱形
C. 当AC=BD时,它是矩形
D. 当∠ABC=90°时,它是矩形
INCLUDEPICTURE"卷8ZJ+39.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+39.EPS" \* MERGEFORMATINET (第4题) INCLUDEPICTURE"卷8ZJ+40.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+40.EPS" \* MERGEFORMATINET (第5题)
5. [数学文化]中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴. 小陶家有一个菱形中国结装饰,其示意图如图,测得BD=12 cm,AC=16 cm,直线EF⊥AB,分别交AB,CD于点E,F,则EF的长为( )
A. 8 cm B. 10 cm C. cm D. cm
6. [2023·INCLUDEPICTURE"学科素养创新意识.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\学科素养创新意识.EPS" \* MERGEFORMATINET 十堰]如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是( )
A. 四边形ABCD由矩形变为平行四边形
B. B,D两点间的距离减少
C. 四边形ABCD的面积不变
D. 四边形ABCD的周长不变
INCLUDEPICTURE"卷8ZJ+41.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+41.EPS" \* MERGEFORMATINET (第6题) INCLUDEPICTURE"卷8ZJ+42.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+42.EPS" \* MERGEFORMATINET (第7题)
7. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连结OE,若OB=4,S菱形ABCD=16,则OE的长为( )
A. 2 B. 4 C. 2 D.
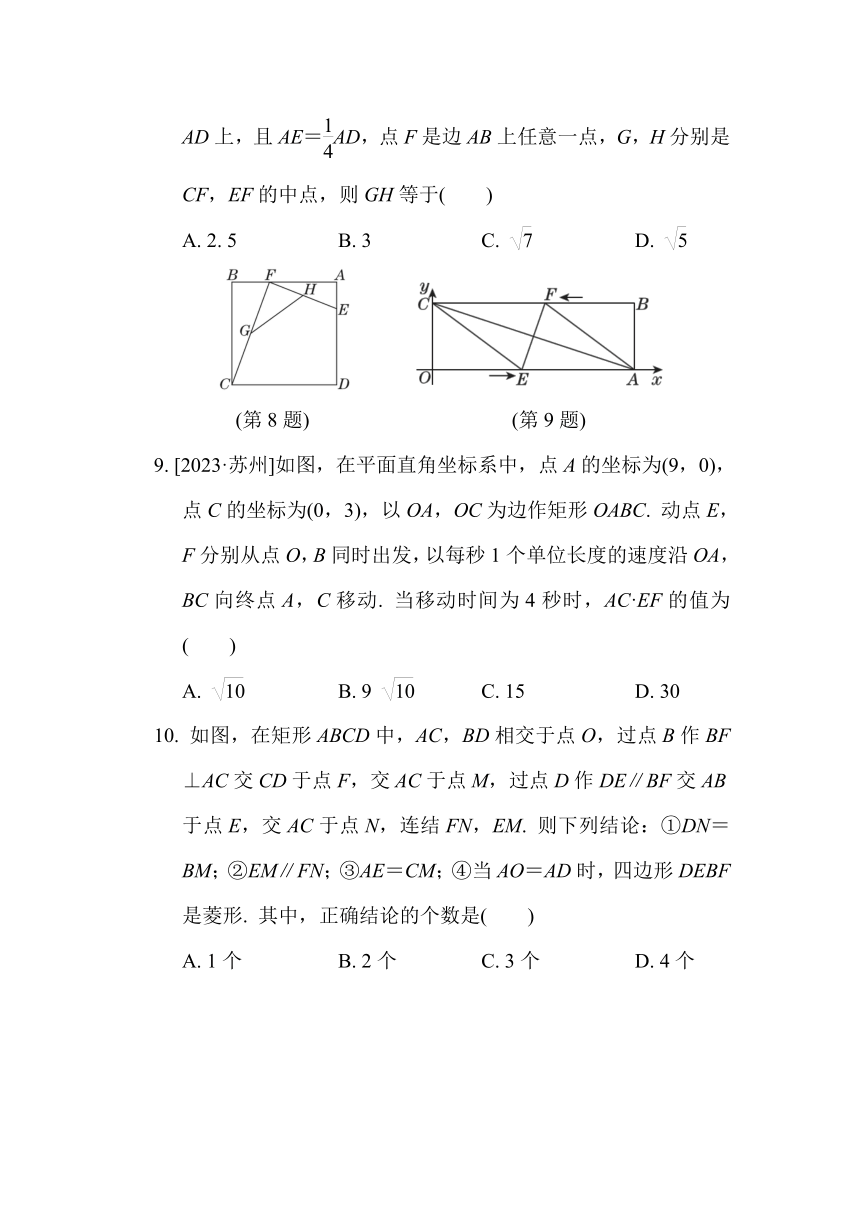
8. [2023·台州二模]如图,在正方形ABCD中,AB=4,点E在边AD上,且AE=AD,点F是边AB上任意一点,G,H分别是CF,EF的中点,则GH等于( )
A. 2. 5 B. 3 C. D.
INCLUDEPICTURE"卷8ZJ+43.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+43.EPS" \* MERGEFORMATINET (第8题) INCLUDEPICTURE"卷8ZJ+44.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+44.EPS" \* MERGEFORMATINET (第9题)
9. [2023·苏州]如图,在平面直角坐标系中,点A的坐标为(9,0),点C的坐标为(0,3),以OA,OC为边作矩形OABC. 动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动. 当移动时间为4秒时,AC·EF的值为( )
A. B. 9 C. 15 D. 30
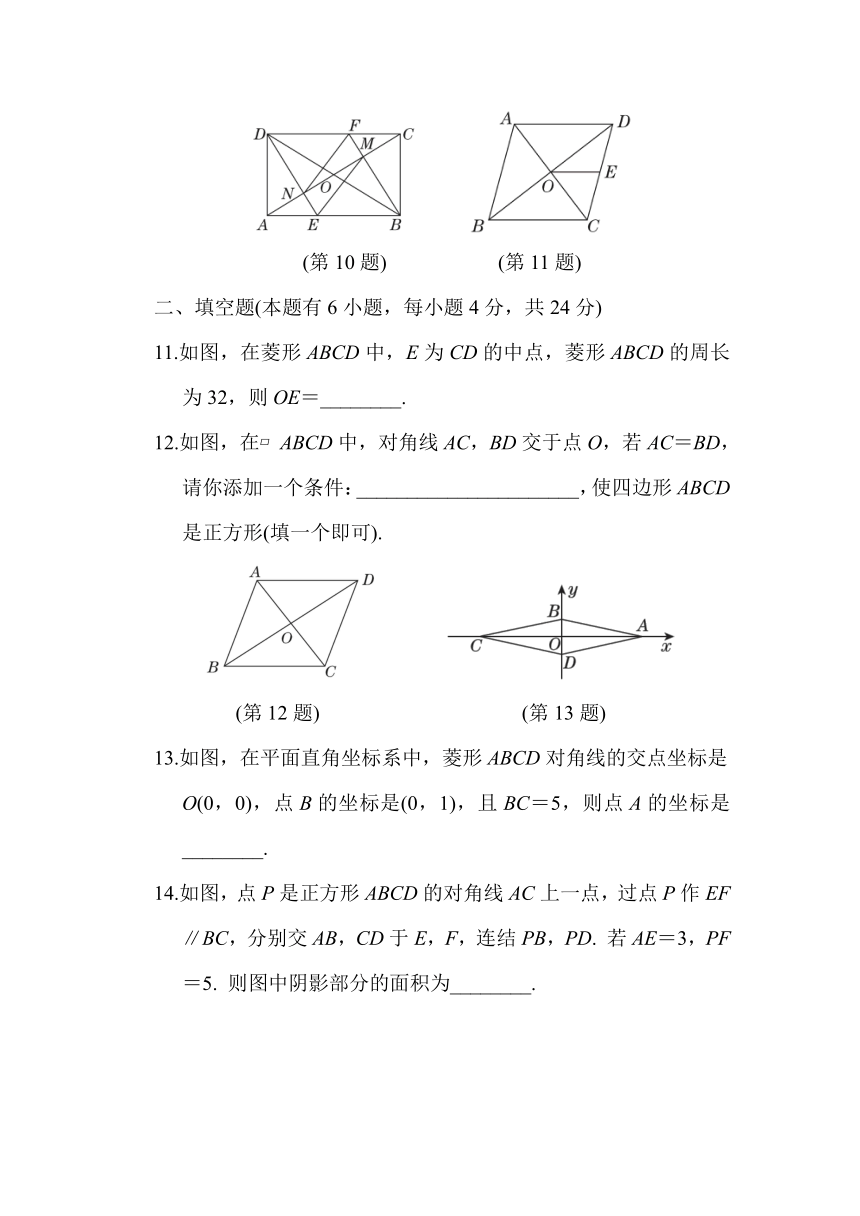
10. 如图,在矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连结FN,EM. 则下列结论:①DN=BM;②EM∥FN;③AE=CM;④当AO=AD时,四边形DEBF是菱形. 其中,正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
INCLUDEPICTURE"卷8ZJ+45.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+45.EPS" \* MERGEFORMATINET (第10题) INCLUDEPICTURE"卷8ZJ+46.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+46.EPS" \* MERGEFORMATINET (第11题)
二、填空题(本题有6小题,每小题4分,共24分)
11.如图,在菱形ABCD中,E为CD的中点,菱形ABCD的周长为32,则OE=________.
12.如图,在 ABCD中,对角线AC,BD交于点O,若AC=BD,请你添加一个条件:______________________,使四边形ABCD是正方形(填一个即可).
INCLUDEPICTURE"卷8ZJ+47.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+47.EPS" \* MERGEFORMATINET (第12题) INCLUDEPICTURE"卷8ZJ+48.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+48.EPS" \* MERGEFORMATINET (第13题)
13.如图,在平面直角坐标系中,菱形ABCD对角线的交点坐标是O(0,0),点B的坐标是(0,1),且BC=5,则点A的坐标是________.
14.如图,点P是正方形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连结PB,PD. 若AE=3,PF=5. 则图中阴影部分的面积为________.
INCLUDEPICTURE"卷8ZJ+49.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+49.EPS" \* MERGEFORMATINET (第14题) INCLUDEPICTURE"卷8ZJ+50.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+50.EPS" \* MERGEFORMATINET (第15题) INCLUDEPICTURE"卷8ZJ+51.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+51.EPS" \* MERGEFORMATINET (第16题)
15.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(点 P不与点A,B 重合),过点P作PE⊥AC于点E,PF⊥BC于点F,连结EF,则EF的最小值是________.
16.[2023·绍兴]如图,在菱形ABCD中,∠DAB=40°,连结AC,以点A为圆心,AC长为半径作弧,交直线AD于点E,连结CE,则∠AEC的度数是________.
三、解答题(本题有8小题,共66分)
17. (6分)如图,菱形ABCD的对角线BD,AC相交于点O,BD=4 cm,AC=6 cm,求菱形ABCD的周长.
INCLUDEPICTURE"一改J1.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\一改J1.EPS" \* MERGEFORMATINET
18. (6 分)如图,在矩形ABCD中,点E是BC边上一点,且DE=AD. 过点A作AF⊥DE于点F,连结AE. 求证:AB=AF.
INCLUDEPICTURE"j-55.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\j-55.EPS" \* MERGEFORMATINET
19. (6 分)[2022·邵阳]如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA. 求证:四边形AECF是正方形.
INCLUDEPICTURE"j-56.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\j-56.EPS" \* MERGEFORMATINET
20. (8 分)[2023·岳阳]如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中:①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是________(填序号);
(2)添加条件后,请证明 ABCD为矩形.
INCLUDEPICTURE"卷8ZJ+56.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+56.EPS" \* MERGEFORMATINET
21. (8 分)[2023·十堰]如图, ABCD的对角线AC,BD交于点O,分别以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P,连结BP,CP.
(1)试判断四边形BPCO的形状,并说明理由;
(2)请说明当 ABCD的对角线满足什么条件时,四边形BPCO是正方形?
INCLUDEPICTURE"卷8ZJ+57.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+57.EPS" \* MERGEFORMATINET
22. (10 分)如图,在△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连结CF.
(1)求证:四边形ADCF是菱形;
(2)若AC=8,菱形ADCF的面积为40,求AB的长.
INCLUDEPICTURE"卷8ZJ+58.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+58.EPS" \* MERGEFORMATINET
23. (10 分)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:△EAB≌△GAD;
(2)求证:BE⊥DG;
(3)若AB=3,AG=3,
求EB的长.
24. (12分) [2023·杭州期中]如图,已知四边形ABCD是菱形,∠B=∠MAN=60°. ∠MAN绕顶点A逆时针旋转,边AM与射线BC相交于点E(点E与点B不重合),边AN与射线CD相交于点F.
(1)当点E在线段BC上时,求证:BE=CF;
(2)连结EF,判断△AEF的形状并说明理由.
INCLUDEPICTURE"卷8ZJ+60.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+60.EPS" \* MERGEFORMATINET
答案
一、1. C 2. D 3. D 4. A 5. C
6. C 【点拨】向左扭动矩形框架ABCD,矩形变成平行四边形,B,D两点间的距离减小,BC边上的高减小,故面积变小,四边形的四条边不变,故周长不变.
7. C 【点拨】∵四边形ABCD是菱形,
∴OA=OC,OB=OD=BD.
∵OB=4,∴BD=2OB=8.
又∵S菱形ABCD=AC·BD=16,∴AC=4.
∵AE⊥BC,∴∠AEC=90°,∴OE=AC=2.
8. A 【点拨】连结CE,∵四边形ABCD是正方形,AB=4,
∴CD=AD=AB=4,∠D=90°.
∵AE=AD,∴AE=1,∴ED=AD-AE=4-1=3,
∴CE===5.
∵G,H分别是CF,EF的中点,
∴GH是△FCE的中位线,∴GH=CE=2. 5.
9. D 【点拨】∵点A的坐标为(9,0),∴OA=9.
∵点C的坐标为(0,3),∴OC=3.
∵∠AOC=90°,
∴AC===3.
∵四边形OABC为矩形,∴AB=OC=3,BC=OA=9,
∴B(9,3). 由题意得OE=BF=4,
∴E(4,0),F(5,3). ∴EF==,
∴AC·EF=3×=30.
10. C 【点拨】∵四边形ABCD是矩形,∴AB=CD,
AB∥CD,AD=BC,AD∥BC,∠DAE=∠BCF=90°,OD=OB=OA=OC,∴∠DAN=∠BCM.
∵BF⊥AC,DE∥BF,∴DE⊥AC,∠BMC=90°.
∴∠DNA=90°=∠BMC. ∴△DNA≌△BMC(AAS),∴DN=BM,∠ADE=∠CBF,故①正确;
∴△ADE≌△CBF(ASA),∴AE=FC,DE=BF.
∵CF>CM,∴AE>CM,故③错误;
∵DE=BF,DN=BM,
∴DE-DN=BF-BM,即NE=MF.
又∵DE∥BF,∴四边形NEMF是平行四边形,
∴EM∥FN,故②正确;
∵AB=CD,AE=CF,∴BE=DF.
又∵BE∥DF,∴四边形DEBF是平行四边形.
当AO=AD时,∵AO=OD,∴AO=AD=OD,
∴△AOD是等边三角形,∴∠ADO=60°,
∴∠ABD=90°-∠ADO=30°.
∵DE⊥AC,∴∠ODN=∠ADO=30°,
∴∠ODN=∠ABD,∴DE=BE,∴ DEBF是菱形,故④正确;∴正确结论的个数是3个.
二、11. 4 12. AC⊥BD(答案不唯一) 13. (2,0)
14. 15 【点拨】如图,过点P作PM⊥AD于点M,MP的延长线交BC于点N. 易得四边形AEFD,
INCLUDEPICTURE"答案8ZJ+27.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\答案8ZJ+27.EPS" \* MERGEFORMATINET
四边形DFPM,四边形BEPN都是矩形,PM=PE,PN=PF,
∴PE=PM=DF=AE=3,
BE=PN=PF=5,
∴S△DFP=S△PBE=×3×5=,
∴S阴影=+=15.
15. 2. 4 【点拨】连结CP. ∵∠ACB=90°,AC=4,BC=3,
∴AB===5.
∵PE⊥AC,PF⊥BC,∴∠PEC=∠PFC=90°.
又∵∠ACB=90°,
∴四边形CFPE是矩形,
∴EF=CP. 易知当CP⊥AB时,CP的值最小,即EF的值最小,当CP⊥AB时,由S△ABC=BC·AC=AB·CP,得×4×3=×5·CP,
∴CP=2. 4. ∴EF的最小值为2. 4.
16. 10°或80°
【点拨】如图,
在菱形ABCD中,
∠DAC=∠BAC,
∵∠DAB=40°,
∴∠DAC=20°.
∵AC=AE,∴∠AEC=×(180°-20°)=80°.
∵AE′=AC,∴∠AE′C=∠ACE′.
又∵∠EAC=∠AE′C+∠ACE′=20°,∴∠AE′C=10°.
综上所述,∠AEC的度数是10°或80°.
三、17. 【解】∵四边形ABCD是菱形,
∴OB=BD,OA=AC,
∠AOB=90°,AB=BC=CD=DA.
又∵BD=4 cm,AC=6 cm,
∴OA=3 cm,OB=2 cm,
∴AB===(cm),
∴菱形ABCD的周长为4AB=4 cm.
18. 【证明】∵AD=DE,∴∠DAE=∠AED.
∵四边形ABCD为矩形,∴AD∥BC,AB⊥BC,
∴∠DAE=∠AEB,∴∠AED=∠AEB,
∴EA平分∠BEF.
∵AF⊥DE,AB⊥BC,∴AB=AF.
19. 【证明】∵ 四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
又∵ BE=DF,∴OB-BE=OD-DF,即OE=OF,
∴四边形AECF是菱形.
∵OE=OA,∴OA=OC=OE=OF,
∴AC=EF. ∴四边形AECF是正方形.
20. (1)①
(2)【证明】∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,∴∠A+∠D=180°.
在△ABM和△DCM中,
∴△ABM≌△DCM(SAS),∴∠A=∠D=90°,
∴ ABCD为矩形.
【点拨】答案不唯一.
21. 【解】(1)四边形BPCO为平行四边形.
理由:∵四边形ABCD为平行四边形,
∴OC=OA=AC,OB=OD=BD.
∵以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P,∴OB=CP,BP=OC,
∴四边形BPCO为平行四边形.
(2)当AC⊥BD,AC=BD时,四边形BPCO为正方形.
由(1)知四边形BPCO为平行四边形.
∵AC⊥BD,∴∠BOC=90°. ∴四边形BPCO为矩形.
∵AC=BD,OB=BD,OC=AC,
∴OB=OC,∴矩形BPCO为正方形.
22. (1)【证明】∵AF∥BC,∴∠AFE=∠DBE.
∵E是AD的中点,∴AE=DE.
在△AFE和△DBE中,∠AFE=∠DBE,∠AEF=∠DEB,AE=DE,
∴△AFE≌△DBE(AAS) ,∴AF=BD.
∵D是BC的中点,∴BD=CD=BC,∴AF=CD.
又∵AF∥BC,∴四边形ADCF是平行四边形.
∵∠BAC=90°,D是BC的中点,
∴AD=BC=CD,∴四边形ADCF是菱形.
(2)【解】连结DF,
∵S菱形ADCF=AC·DF=40,AC=8,∴DF=10.
∵AF∥BC,AF=BD,
∴四边形ABDF是平行四边形,∴AB=DF=10.
23. (1)【证明】∵四边形ABCD、四边形AGFE是正方形,∴AB=AD,AE=AG,∠DAB=∠EAG=90°,
∴∠EAB=∠GAD. ∴△EAB≌△GAD(SAS).
(2)【证明】∵△EAB≌△GAD,∴∠AEB=∠AGD.
∵∠AMG=∠HME,
∴∠HEM+∠HME=∠AGM+∠AMG=180°-∠GAM=90°,∴∠MHE=90°,∴BE⊥DG.
(3)【解】∵△EAB≌△GAD,∴EB=GD.
∵四边形ABCD是正方形,AB=3,
∴BD⊥AC,AC=BD=AB=6,OA=AC, OD=BD,∴∠DOG=90°,OA=OD=3.
∵AG=3,∴OG=OA+AG=6,
∴GD===3,∴EB=3.
24. (1)【证明】连结AC. ∵四边形ABCD是菱形,
∴AB=BC,AB∥CD,∴∠BAC=∠ACD.
∵∠B=60°,∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠ACD=∠BAC=60°=∠B,
∠BAE+∠MAC=60°.
又∵∠MAN=∠CAF+∠MAC=60°,
∴∠BAE=∠CAF.
在△ABE和△ACF中,
∴△ABE≌△ACF(ASA),∴BE=CF.
(2)【解】△AEF是等边三角形,理由如下:
当点E在线段BC上时,
由(1)知△ABE≌△ACF,∴AE=AF.
∵∠MAN=60°,∴△AEF是等边三角形;
当点E在线段BC的延长线上时,连结AC,如图,
INCLUDEPICTURE"答案8ZJ+29.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\答案8ZJ+29.EPS" \* MERGEFORMATINET
∵四边形ABCD是菱形,∠B=60°,
∴AD∥BC,∠ADC=∠B=60°,AB=AD,
∴∠DAC=∠ACB,∠ADF=120°.
由(1)知△ABC是等边三角形,∴∠ACB=60°,
∴∠DAC=60°,∠ACE=120°,∴∠ACE=∠ADF.
由(1)知AB=AC,∴AC=AD.
∵∠DAC=60°,∴∠DAE+∠MAC=60°.
又∵∠MAN=∠DAE+∠NAD=60°,
∴∠MAC=∠NAD.
在△ACE和△ADF中,
∴△ACE≌△ADF(ASA). ∴AE=AF.
又∵∠MAN=60°,∴△AEF是等边三角形.
一、选择题(本题有10小题,每小题3分,共30分)
1. [2023·台州临海市期中]如图,在矩形ABCD中,对角线AC,BD交于点O,如果∠ADB=32°,那么∠AOB的度数为( )
A. 32° B. 48° C. 64° D. 96°
INCLUDEPICTURE"卷8ZJ+37.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+37.EPS" \* MERGEFORMATINET (第1题) INCLUDEPICTURE"卷8ZJ+38.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+38.EPS" \* MERGEFORMATINET (第3题)
2. 菱形、矩形、正方形都具有的性质是( )
A. 四条边相等,四个角相等 B. 对角线相等
C. 对角线互相垂直 D. 对角线互相平分
3. 如图,以正方形ABCD的对角线AC为一边作菱形AEFC,则∠FAB的度数是( )
A. 20° B. 30° C. 50° D. 22. 5°
4. 如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A. 当AB=BC时,它是正方形 B. 当AC⊥BD时,它是菱形
C. 当AC=BD时,它是矩形
D. 当∠ABC=90°时,它是矩形
INCLUDEPICTURE"卷8ZJ+39.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+39.EPS" \* MERGEFORMATINET (第4题) INCLUDEPICTURE"卷8ZJ+40.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+40.EPS" \* MERGEFORMATINET (第5题)
5. [数学文化]中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴. 小陶家有一个菱形中国结装饰,其示意图如图,测得BD=12 cm,AC=16 cm,直线EF⊥AB,分别交AB,CD于点E,F,则EF的长为( )
A. 8 cm B. 10 cm C. cm D. cm
6. [2023·INCLUDEPICTURE"学科素养创新意识.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\学科素养创新意识.EPS" \* MERGEFORMATINET 十堰]如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是( )
A. 四边形ABCD由矩形变为平行四边形
B. B,D两点间的距离减少
C. 四边形ABCD的面积不变
D. 四边形ABCD的周长不变
INCLUDEPICTURE"卷8ZJ+41.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+41.EPS" \* MERGEFORMATINET (第6题) INCLUDEPICTURE"卷8ZJ+42.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+42.EPS" \* MERGEFORMATINET (第7题)
7. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连结OE,若OB=4,S菱形ABCD=16,则OE的长为( )
A. 2 B. 4 C. 2 D.
8. [2023·台州二模]如图,在正方形ABCD中,AB=4,点E在边AD上,且AE=AD,点F是边AB上任意一点,G,H分别是CF,EF的中点,则GH等于( )
A. 2. 5 B. 3 C. D.
INCLUDEPICTURE"卷8ZJ+43.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+43.EPS" \* MERGEFORMATINET (第8题) INCLUDEPICTURE"卷8ZJ+44.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+44.EPS" \* MERGEFORMATINET (第9题)
9. [2023·苏州]如图,在平面直角坐标系中,点A的坐标为(9,0),点C的坐标为(0,3),以OA,OC为边作矩形OABC. 动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动. 当移动时间为4秒时,AC·EF的值为( )
A. B. 9 C. 15 D. 30
10. 如图,在矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连结FN,EM. 则下列结论:①DN=BM;②EM∥FN;③AE=CM;④当AO=AD时,四边形DEBF是菱形. 其中,正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
INCLUDEPICTURE"卷8ZJ+45.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+45.EPS" \* MERGEFORMATINET (第10题) INCLUDEPICTURE"卷8ZJ+46.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+46.EPS" \* MERGEFORMATINET (第11题)
二、填空题(本题有6小题,每小题4分,共24分)
11.如图,在菱形ABCD中,E为CD的中点,菱形ABCD的周长为32,则OE=________.
12.如图,在 ABCD中,对角线AC,BD交于点O,若AC=BD,请你添加一个条件:______________________,使四边形ABCD是正方形(填一个即可).
INCLUDEPICTURE"卷8ZJ+47.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+47.EPS" \* MERGEFORMATINET (第12题) INCLUDEPICTURE"卷8ZJ+48.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+48.EPS" \* MERGEFORMATINET (第13题)
13.如图,在平面直角坐标系中,菱形ABCD对角线的交点坐标是O(0,0),点B的坐标是(0,1),且BC=5,则点A的坐标是________.
14.如图,点P是正方形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连结PB,PD. 若AE=3,PF=5. 则图中阴影部分的面积为________.
INCLUDEPICTURE"卷8ZJ+49.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+49.EPS" \* MERGEFORMATINET (第14题) INCLUDEPICTURE"卷8ZJ+50.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+50.EPS" \* MERGEFORMATINET (第15题) INCLUDEPICTURE"卷8ZJ+51.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+51.EPS" \* MERGEFORMATINET (第16题)
15.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(点 P不与点A,B 重合),过点P作PE⊥AC于点E,PF⊥BC于点F,连结EF,则EF的最小值是________.
16.[2023·绍兴]如图,在菱形ABCD中,∠DAB=40°,连结AC,以点A为圆心,AC长为半径作弧,交直线AD于点E,连结CE,则∠AEC的度数是________.
三、解答题(本题有8小题,共66分)
17. (6分)如图,菱形ABCD的对角线BD,AC相交于点O,BD=4 cm,AC=6 cm,求菱形ABCD的周长.
INCLUDEPICTURE"一改J1.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\一改J1.EPS" \* MERGEFORMATINET
18. (6 分)如图,在矩形ABCD中,点E是BC边上一点,且DE=AD. 过点A作AF⊥DE于点F,连结AE. 求证:AB=AF.
INCLUDEPICTURE"j-55.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\j-55.EPS" \* MERGEFORMATINET
19. (6 分)[2022·邵阳]如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA. 求证:四边形AECF是正方形.
INCLUDEPICTURE"j-56.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\j-56.EPS" \* MERGEFORMATINET
20. (8 分)[2023·岳阳]如图,点M在 ABCD的边AD上,BM=CM,请从以下三个选项中:①∠1=∠2;②AM=DM;③∠3=∠4,选择一个合适的选项作为已知条件,使 ABCD为矩形.
(1)你添加的条件是________(填序号);
(2)添加条件后,请证明 ABCD为矩形.
INCLUDEPICTURE"卷8ZJ+56.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+56.EPS" \* MERGEFORMATINET
21. (8 分)[2023·十堰]如图, ABCD的对角线AC,BD交于点O,分别以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P,连结BP,CP.
(1)试判断四边形BPCO的形状,并说明理由;
(2)请说明当 ABCD的对角线满足什么条件时,四边形BPCO是正方形?
INCLUDEPICTURE"卷8ZJ+57.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+57.EPS" \* MERGEFORMATINET
22. (10 分)如图,在△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连结CF.
(1)求证:四边形ADCF是菱形;
(2)若AC=8,菱形ADCF的面积为40,求AB的长.
INCLUDEPICTURE"卷8ZJ+58.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+58.EPS" \* MERGEFORMATINET
23. (10 分)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:△EAB≌△GAD;
(2)求证:BE⊥DG;
(3)若AB=3,AG=3,
求EB的长.
24. (12分) [2023·杭州期中]如图,已知四边形ABCD是菱形,∠B=∠MAN=60°. ∠MAN绕顶点A逆时针旋转,边AM与射线BC相交于点E(点E与点B不重合),边AN与射线CD相交于点F.
(1)当点E在线段BC上时,求证:BE=CF;
(2)连结EF,判断△AEF的形状并说明理由.
INCLUDEPICTURE"卷8ZJ+60.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\卷8ZJ+60.EPS" \* MERGEFORMATINET
答案
一、1. C 2. D 3. D 4. A 5. C
6. C 【点拨】向左扭动矩形框架ABCD,矩形变成平行四边形,B,D两点间的距离减小,BC边上的高减小,故面积变小,四边形的四条边不变,故周长不变.
7. C 【点拨】∵四边形ABCD是菱形,
∴OA=OC,OB=OD=BD.
∵OB=4,∴BD=2OB=8.
又∵S菱形ABCD=AC·BD=16,∴AC=4.
∵AE⊥BC,∴∠AEC=90°,∴OE=AC=2.
8. A 【点拨】连结CE,∵四边形ABCD是正方形,AB=4,
∴CD=AD=AB=4,∠D=90°.
∵AE=AD,∴AE=1,∴ED=AD-AE=4-1=3,
∴CE===5.
∵G,H分别是CF,EF的中点,
∴GH是△FCE的中位线,∴GH=CE=2. 5.
9. D 【点拨】∵点A的坐标为(9,0),∴OA=9.
∵点C的坐标为(0,3),∴OC=3.
∵∠AOC=90°,
∴AC===3.
∵四边形OABC为矩形,∴AB=OC=3,BC=OA=9,
∴B(9,3). 由题意得OE=BF=4,
∴E(4,0),F(5,3). ∴EF==,
∴AC·EF=3×=30.
10. C 【点拨】∵四边形ABCD是矩形,∴AB=CD,
AB∥CD,AD=BC,AD∥BC,∠DAE=∠BCF=90°,OD=OB=OA=OC,∴∠DAN=∠BCM.
∵BF⊥AC,DE∥BF,∴DE⊥AC,∠BMC=90°.
∴∠DNA=90°=∠BMC. ∴△DNA≌△BMC(AAS),∴DN=BM,∠ADE=∠CBF,故①正确;
∴△ADE≌△CBF(ASA),∴AE=FC,DE=BF.
∵CF>CM,∴AE>CM,故③错误;
∵DE=BF,DN=BM,
∴DE-DN=BF-BM,即NE=MF.
又∵DE∥BF,∴四边形NEMF是平行四边形,
∴EM∥FN,故②正确;
∵AB=CD,AE=CF,∴BE=DF.
又∵BE∥DF,∴四边形DEBF是平行四边形.
当AO=AD时,∵AO=OD,∴AO=AD=OD,
∴△AOD是等边三角形,∴∠ADO=60°,
∴∠ABD=90°-∠ADO=30°.
∵DE⊥AC,∴∠ODN=∠ADO=30°,
∴∠ODN=∠ABD,∴DE=BE,∴ DEBF是菱形,故④正确;∴正确结论的个数是3个.
二、11. 4 12. AC⊥BD(答案不唯一) 13. (2,0)
14. 15 【点拨】如图,过点P作PM⊥AD于点M,MP的延长线交BC于点N. 易得四边形AEFD,
INCLUDEPICTURE"答案8ZJ+27.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\答案8ZJ+27.EPS" \* MERGEFORMATINET
四边形DFPM,四边形BEPN都是矩形,PM=PE,PN=PF,
∴PE=PM=DF=AE=3,
BE=PN=PF=5,
∴S△DFP=S△PBE=×3×5=,
∴S阴影=+=15.
15. 2. 4 【点拨】连结CP. ∵∠ACB=90°,AC=4,BC=3,
∴AB===5.
∵PE⊥AC,PF⊥BC,∴∠PEC=∠PFC=90°.
又∵∠ACB=90°,
∴四边形CFPE是矩形,
∴EF=CP. 易知当CP⊥AB时,CP的值最小,即EF的值最小,当CP⊥AB时,由S△ABC=BC·AC=AB·CP,得×4×3=×5·CP,
∴CP=2. 4. ∴EF的最小值为2. 4.
16. 10°或80°
【点拨】如图,
在菱形ABCD中,
∠DAC=∠BAC,
∵∠DAB=40°,
∴∠DAC=20°.
∵AC=AE,∴∠AEC=×(180°-20°)=80°.
∵AE′=AC,∴∠AE′C=∠ACE′.
又∵∠EAC=∠AE′C+∠ACE′=20°,∴∠AE′C=10°.
综上所述,∠AEC的度数是10°或80°.
三、17. 【解】∵四边形ABCD是菱形,
∴OB=BD,OA=AC,
∠AOB=90°,AB=BC=CD=DA.
又∵BD=4 cm,AC=6 cm,
∴OA=3 cm,OB=2 cm,
∴AB===(cm),
∴菱形ABCD的周长为4AB=4 cm.
18. 【证明】∵AD=DE,∴∠DAE=∠AED.
∵四边形ABCD为矩形,∴AD∥BC,AB⊥BC,
∴∠DAE=∠AEB,∴∠AED=∠AEB,
∴EA平分∠BEF.
∵AF⊥DE,AB⊥BC,∴AB=AF.
19. 【证明】∵ 四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
又∵ BE=DF,∴OB-BE=OD-DF,即OE=OF,
∴四边形AECF是菱形.
∵OE=OA,∴OA=OC=OE=OF,
∴AC=EF. ∴四边形AECF是正方形.
20. (1)①
(2)【证明】∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,∴∠A+∠D=180°.
在△ABM和△DCM中,
∴△ABM≌△DCM(SAS),∴∠A=∠D=90°,
∴ ABCD为矩形.
【点拨】答案不唯一.
21. 【解】(1)四边形BPCO为平行四边形.
理由:∵四边形ABCD为平行四边形,
∴OC=OA=AC,OB=OD=BD.
∵以点B,C为圆心,AC,BD长为半径画弧,两弧交于点P,∴OB=CP,BP=OC,
∴四边形BPCO为平行四边形.
(2)当AC⊥BD,AC=BD时,四边形BPCO为正方形.
由(1)知四边形BPCO为平行四边形.
∵AC⊥BD,∴∠BOC=90°. ∴四边形BPCO为矩形.
∵AC=BD,OB=BD,OC=AC,
∴OB=OC,∴矩形BPCO为正方形.
22. (1)【证明】∵AF∥BC,∴∠AFE=∠DBE.
∵E是AD的中点,∴AE=DE.
在△AFE和△DBE中,∠AFE=∠DBE,∠AEF=∠DEB,AE=DE,
∴△AFE≌△DBE(AAS) ,∴AF=BD.
∵D是BC的中点,∴BD=CD=BC,∴AF=CD.
又∵AF∥BC,∴四边形ADCF是平行四边形.
∵∠BAC=90°,D是BC的中点,
∴AD=BC=CD,∴四边形ADCF是菱形.
(2)【解】连结DF,
∵S菱形ADCF=AC·DF=40,AC=8,∴DF=10.
∵AF∥BC,AF=BD,
∴四边形ABDF是平行四边形,∴AB=DF=10.
23. (1)【证明】∵四边形ABCD、四边形AGFE是正方形,∴AB=AD,AE=AG,∠DAB=∠EAG=90°,
∴∠EAB=∠GAD. ∴△EAB≌△GAD(SAS).
(2)【证明】∵△EAB≌△GAD,∴∠AEB=∠AGD.
∵∠AMG=∠HME,
∴∠HEM+∠HME=∠AGM+∠AMG=180°-∠GAM=90°,∴∠MHE=90°,∴BE⊥DG.
(3)【解】∵△EAB≌△GAD,∴EB=GD.
∵四边形ABCD是正方形,AB=3,
∴BD⊥AC,AC=BD=AB=6,OA=AC, OD=BD,∴∠DOG=90°,OA=OD=3.
∵AG=3,∴OG=OA+AG=6,
∴GD===3,∴EB=3.
24. (1)【证明】连结AC. ∵四边形ABCD是菱形,
∴AB=BC,AB∥CD,∴∠BAC=∠ACD.
∵∠B=60°,∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠ACD=∠BAC=60°=∠B,
∠BAE+∠MAC=60°.
又∵∠MAN=∠CAF+∠MAC=60°,
∴∠BAE=∠CAF.
在△ABE和△ACF中,
∴△ABE≌△ACF(ASA),∴BE=CF.
(2)【解】△AEF是等边三角形,理由如下:
当点E在线段BC上时,
由(1)知△ABE≌△ACF,∴AE=AF.
∵∠MAN=60°,∴△AEF是等边三角形;
当点E在线段BC的延长线上时,连结AC,如图,
INCLUDEPICTURE"答案8ZJ+29.EPS" INCLUDEPICTURE \d "D:\\24春\\24春 典中点 8 数学 ZJ(做测试卷\\答案8ZJ+29.EPS" \* MERGEFORMATINET
∵四边形ABCD是菱形,∠B=60°,
∴AD∥BC,∠ADC=∠B=60°,AB=AD,
∴∠DAC=∠ACB,∠ADF=120°.
由(1)知△ABC是等边三角形,∴∠ACB=60°,
∴∠DAC=60°,∠ACE=120°,∴∠ACE=∠ADF.
由(1)知AB=AC,∴AC=AD.
∵∠DAC=60°,∴∠DAE+∠MAC=60°.
又∵∠MAN=∠DAE+∠NAD=60°,
∴∠MAC=∠NAD.
在△ACE和△ADF中,
∴△ACE≌△ADF(ASA). ∴AE=AF.
又∵∠MAN=60°,∴△AEF是等边三角形.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
