5.1多边形(1)(浙江省宁波市江东区)
文档属性
| 名称 | 5.1多边形(1)(浙江省宁波市江东区) |  | |
| 格式 | rar | ||
| 文件大小 | 398.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-28 19:00:00 | ||
图片预览





文档简介
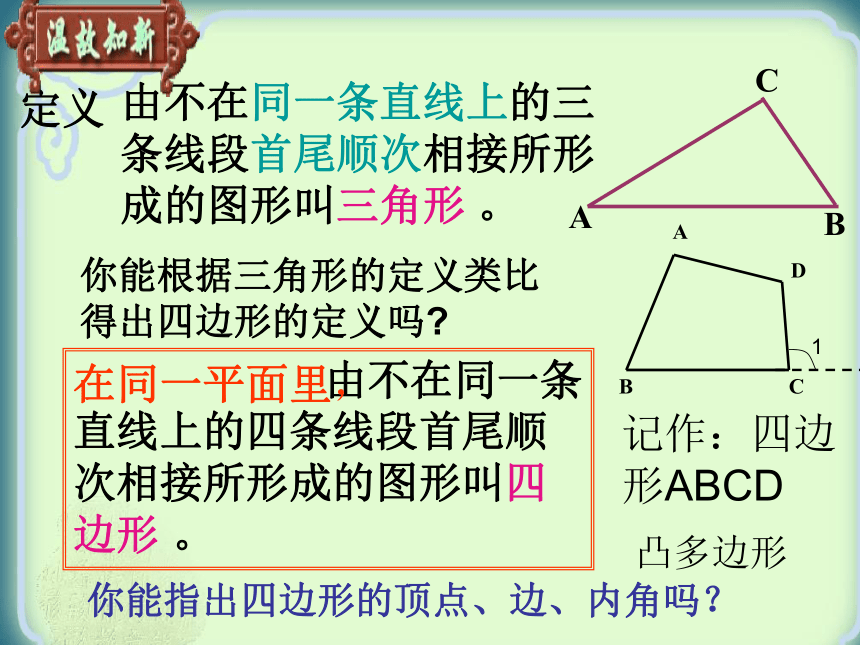
课件18张PPT。5.1 多边形第一课 四边形小明家有一间木材加工场,发现有很多各种形状的余料,你能从图中找出你所熟悉的几何图形吗?定义 由不在同一条直线上的三条线段首尾顺次相接所形成的图形叫三角形 。ABC 由不在同一条直线上的四条线段首尾顺次相接所形成的图形叫四边形 。 你能根据三角形的定义类比得出四边形的定义吗?在同一平面里, 你能指出四边形的顶点、边、内角吗?记作:四边形ABCD凸多边形 本着节约资源和保护环境的想法,小明想将其中的一些四边形余料(规格一样)拼成无缝隙的地板,但试了一段时间没成功?那么是不是这些四边形材料就不能拼成无缝隙的地板呢?实验并猜想:方案二:利用手中的四边形,量出四个内角的度数,并标记在角上,算出这个四边形内角和.方案一:利用手中的四边形,挑选其中一个将
四个角标为∠1 ∠2 ∠3 ∠4,把这四个角剪下
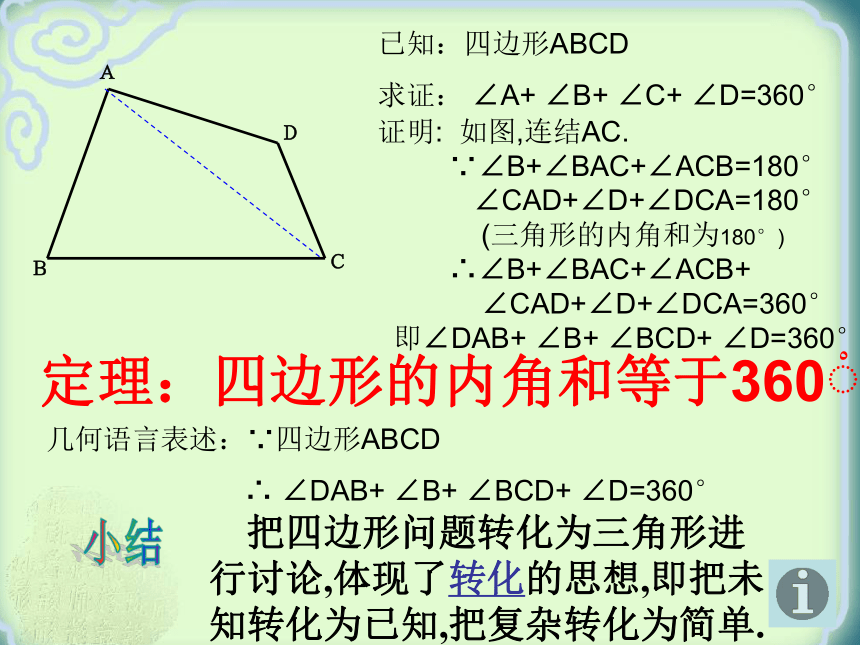
后拼在一起(四个角的顶点重合),你发现什么?前后两桌四个同学为一组,拿出放在信封里的四边形,通过下列方案探索四边形的内角和: 你能否利用以前学过的几何知识来证明四边形的内角和为360度呢?实验不等于证明!证明: 如图,连结AC.
∵∠B+∠BAC+∠ACB=180°
∠CAD+∠D+∠DCA=180°
(三角形的内角和为180°)
∴∠B+∠BAC+∠ACB+
∠CAD+∠D+∠DCA=360°
即∠DAB+ ∠B+ ∠BCD+ ∠D=360° 把四边形问题转化为三角形进行讨论,体现了转化的思想,即把未知转化为已知,把复杂转化为简单.小结定理:四边形的内角和等于360?已知:四边形ABCD
求证: ∠A+ ∠B+ ∠C+ ∠D=360°几何语言表述:∵四边形ABCD
∴ ∠DAB+ ∠B+ ∠BCD+ ∠D=360° 在每个顶点处取这个四边形的一个外角,它们的和叫做这个四边形的外角和。推论:(能够由一个定理直接推理得到的真命题叫做这个定理的推论)
四边形的外角和等于360?想一想:利用四边形的内角和定理能推理得到四边形的外角和多少?几何语言表述:∵四边形ABCD
∴ ∠1+ ∠2+ ∠3+ ∠4=360°例:如图,四边形风筝的四个内角分别为∠ A,∠B ,∠C ,∠D(3) 若∠ A,∠B ,∠C ,∠D的度数之比为1: 1: 0.6: 1求它的四个内角的度数。(1)若其中三个内角分别为55。、94。、105。,求第四个内角?(2)若∠A和∠C互补, ∠B=85。
求∠D?头脑风暴 (1)四边形中有二个内角分别为72?、89?、第三个内角的外角为115?、求第四个内角的度数.
(2) 一个四边形的四个内角之比 1:2:3:4.求四个内角的度数.
(3)已知四边形ABCD中, ∠A与∠C互补.∠B比∠D大15?, 求∠D的度数.巩固练习数学学习者数学爱好者小数学天才小小数学家荣誉级别晋升规则:
从低级到高级逐步提高已知:如图,直线OB⊥AB,垂足为B,直线OC⊥AC,垂足为C. (1)∠1与 ∠ A之间有什么关系;
(2) 图中有与∠ A相等的角吗?若有请指出 并说明.1AC数学学习者试题清晨,小明沿着一个四边形广场周围的小路,按逆时针方向跑步.(1)小明每从一条小路转到下一条小路时,身体转过的角是哪个角?(2)他每跑完一圈,
身体转过的角度之和
是多少?数学爱好者试题 现在你能利用手中规格一样的四边形余料,拼成无缝隙的地板吗?如果能的话,这是利用了四边形的什么性质呢?四边形的内角和=360°小数学天才试题在刚才的四边形内角和定理
证明中,除了书上的证法外,
你还能想出其他至少三种以
上的方法么?小小数学家试题1.本课学习的哪些数学知识三角形的概念 四边形的概念
四边形问题 三角形问题类比转化(已知)(未知)(未知)(已知)2.本课学习的哪些数学思想这节课你有何收获?再见引伸拓展在证明四边形内角和的基础上,你能探求五边形、六边形和一般的n边形的内角和性质吗?请课后思考,并作为课外活动小组活动的内容。
四个角标为∠1 ∠2 ∠3 ∠4,把这四个角剪下
后拼在一起(四个角的顶点重合),你发现什么?前后两桌四个同学为一组,拿出放在信封里的四边形,通过下列方案探索四边形的内角和: 你能否利用以前学过的几何知识来证明四边形的内角和为360度呢?实验不等于证明!证明: 如图,连结AC.
∵∠B+∠BAC+∠ACB=180°
∠CAD+∠D+∠DCA=180°
(三角形的内角和为180°)
∴∠B+∠BAC+∠ACB+
∠CAD+∠D+∠DCA=360°
即∠DAB+ ∠B+ ∠BCD+ ∠D=360° 把四边形问题转化为三角形进行讨论,体现了转化的思想,即把未知转化为已知,把复杂转化为简单.小结定理:四边形的内角和等于360?已知:四边形ABCD
求证: ∠A+ ∠B+ ∠C+ ∠D=360°几何语言表述:∵四边形ABCD
∴ ∠DAB+ ∠B+ ∠BCD+ ∠D=360° 在每个顶点处取这个四边形的一个外角,它们的和叫做这个四边形的外角和。推论:(能够由一个定理直接推理得到的真命题叫做这个定理的推论)
四边形的外角和等于360?想一想:利用四边形的内角和定理能推理得到四边形的外角和多少?几何语言表述:∵四边形ABCD
∴ ∠1+ ∠2+ ∠3+ ∠4=360°例:如图,四边形风筝的四个内角分别为∠ A,∠B ,∠C ,∠D(3) 若∠ A,∠B ,∠C ,∠D的度数之比为1: 1: 0.6: 1求它的四个内角的度数。(1)若其中三个内角分别为55。、94。、105。,求第四个内角?(2)若∠A和∠C互补, ∠B=85。
求∠D?头脑风暴 (1)四边形中有二个内角分别为72?、89?、第三个内角的外角为115?、求第四个内角的度数.
(2) 一个四边形的四个内角之比 1:2:3:4.求四个内角的度数.
(3)已知四边形ABCD中, ∠A与∠C互补.∠B比∠D大15?, 求∠D的度数.巩固练习数学学习者数学爱好者小数学天才小小数学家荣誉级别晋升规则:
从低级到高级逐步提高已知:如图,直线OB⊥AB,垂足为B,直线OC⊥AC,垂足为C. (1)∠1与 ∠ A之间有什么关系;
(2) 图中有与∠ A相等的角吗?若有请指出 并说明.1AC数学学习者试题清晨,小明沿着一个四边形广场周围的小路,按逆时针方向跑步.(1)小明每从一条小路转到下一条小路时,身体转过的角是哪个角?(2)他每跑完一圈,
身体转过的角度之和
是多少?数学爱好者试题 现在你能利用手中规格一样的四边形余料,拼成无缝隙的地板吗?如果能的话,这是利用了四边形的什么性质呢?四边形的内角和=360°小数学天才试题在刚才的四边形内角和定理
证明中,除了书上的证法外,
你还能想出其他至少三种以
上的方法么?小小数学家试题1.本课学习的哪些数学知识三角形的概念 四边形的概念
四边形问题 三角形问题类比转化(已知)(未知)(未知)(已知)2.本课学习的哪些数学思想这节课你有何收获?再见引伸拓展在证明四边形内角和的基础上,你能探求五边形、六边形和一般的n边形的内角和性质吗?请课后思考,并作为课外活动小组活动的内容。
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
