2023届浙教版八年级上册第四章《4.2.2平面直角坐标系》课时练习(含答案)
文档属性
| 名称 | 2023届浙教版八年级上册第四章《4.2.2平面直角坐标系》课时练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-18 10:13:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.2.2平面直角坐标系
一、夯实基础
1.已知点M(1,-2),N(-3,-2),则直线MN与x轴,y轴的位置关系分别为( )
A.相交,相交 B.平行,垂直相交 C.垂直相交,平行 D.平行,平行
2.已知A(-2,4),B(2,4),那么线段AB的长度是( )
A.4 B.6 C.8 D.无法确定
3.若点P(2,-4),Q(x,-4)之间的距离是3,则x的值为( )
A.3 B.5 C.-1 D.5或-1
4.在方格纸上有A,B两点,若以点B为原点建立直角坐标系,则点A的坐标为(2,5),若以点A为原点建立直角坐标系,则点B的坐标为( )
A.(-2,-5) B.(-2,5) C.(2,-5) D.(2,5)
5.如图所示,将长为3cm的长方形ABCD放在平面直角坐标系中,若点D
的坐标为(6,3),则点A的坐标为( )
A.(5,3) B.(4,3) C.(4,2) D.(3,3)
6.下列说法中,错误的是( )
A.平行于x轴的直线上的所有点的纵坐标相同
B.平行于y轴的直线上的所有点的横坐标相同
C.若点P(a,b)在x轴上,则a=0
D.(-3,4)与(4,-3)表示两个不同的点
在直角坐标系中,点A的坐标为(4,3),点B的坐标为(4,2),O为坐标原点,则△AOB
的面积为 .
“健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的
活动场地定在奥林匹克公园.所走路线如图所示:森林公园—玲珑
塔—国家体育场—水立方.若在奥林匹克公园设计图上玲珑塔的坐
标为(-1,0),森林公园的坐标为(-2,2),那么地图线不变时, 水
立方的坐标为 .
如图,已知一个长方形的长为8,宽为4,请建立适当的直角坐标
系,并求出A,B,C,D四点的坐标.
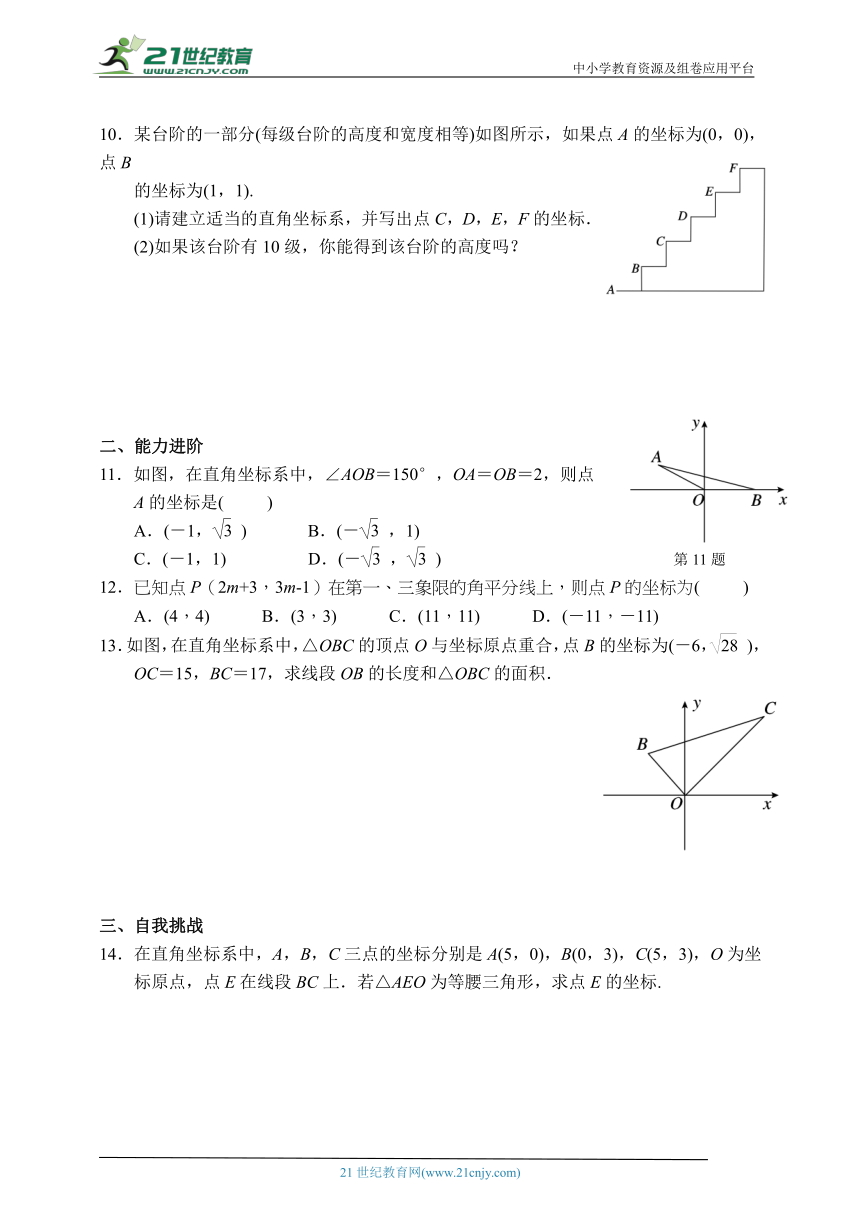
某台阶的一部分(每级台阶的高度和宽度相等)如图所示,如果点A的坐标为(0,0),点B
的坐标为(1,1).
(1)请建立适当的直角坐标系,并写出点C,D,E,F的坐标.
(2)如果该台阶有10级,你能得到该台阶的高度吗?
二、能力进阶
11.如图,在直角坐标系中,∠AOB=150°,OA=OB=2,则点
A的坐标是( )
A.(-1,) B.(-,1)
C.(-1,1) D.(-,)
12.已知点P(2m+3,3m-1)在第一、三象限的角平分线上,则点P的坐标为( )
A.(4,4) B.(3,3) C.(11,11) D.(-11,-11)
13.如图,在直角坐标系中,△OBC的顶点O与坐标原点重合,点B的坐标为(-6,),OC=15,BC=17,求线段OB的长度和△OBC的面积.
三、自我挑战
14.在直角坐标系中,A,B,C三点的坐标分别是A(5,0),B(0,3),C(5,3),O为坐标原点,点E在线段BC上.若△AEO为等腰三角形,求点E的坐标.
【参考答案】
1.B
2.A
3.D
4.A
5.D
6.C
7.2 .
8. (-2,-4)
9.解:如图,以C为原点,直线CB为x轴,直线CD为y轴建立直角坐标系.则A(8,4),B(8,0),C(0,0),D(0,4).(答案不唯一)
第9题答图
10.解:(1)如图,以点A为原点,水平方向为x轴,竖直方向为y轴建立直角坐标系.
∴点C,D,E,F的坐标分别为C(2,2),D(3,3),E(4,4),F(5,5).
(2)∵每级台阶高为1,∴10级台阶的高度是10.
B
C
13.解:如图,过点B作BM⊥x轴于点M.
∵点B的坐标为(-6,),
∴OM=6,BM=.
由勾股定理得
OB2=OM2+BM2=62+()2=64,
∴OB=8.
又∵OC=15,BC=17,
∴OB2+OC2=BC2,
∴△OBC是直角三角形,且∠BOC=90°,
∴S△OBC=×8×15=60.
14.解:如图所示.
若A为顶角顶点,则AE1=AO,故点E1(1,3);
若E为顶角顶点,则E2O=E2A,故点E2(2.5,3);
若O为顶角顶点,则OE3=OA,故点E3(4,3).
综上所述,点E的坐标为(1,3)或(2.5,3)或(4,3).
第5题
第8题
第11题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.2.2平面直角坐标系
一、夯实基础
1.已知点M(1,-2),N(-3,-2),则直线MN与x轴,y轴的位置关系分别为( )
A.相交,相交 B.平行,垂直相交 C.垂直相交,平行 D.平行,平行
2.已知A(-2,4),B(2,4),那么线段AB的长度是( )
A.4 B.6 C.8 D.无法确定
3.若点P(2,-4),Q(x,-4)之间的距离是3,则x的值为( )
A.3 B.5 C.-1 D.5或-1
4.在方格纸上有A,B两点,若以点B为原点建立直角坐标系,则点A的坐标为(2,5),若以点A为原点建立直角坐标系,则点B的坐标为( )
A.(-2,-5) B.(-2,5) C.(2,-5) D.(2,5)
5.如图所示,将长为3cm的长方形ABCD放在平面直角坐标系中,若点D
的坐标为(6,3),则点A的坐标为( )
A.(5,3) B.(4,3) C.(4,2) D.(3,3)
6.下列说法中,错误的是( )
A.平行于x轴的直线上的所有点的纵坐标相同
B.平行于y轴的直线上的所有点的横坐标相同
C.若点P(a,b)在x轴上,则a=0
D.(-3,4)与(4,-3)表示两个不同的点
在直角坐标系中,点A的坐标为(4,3),点B的坐标为(4,2),O为坐标原点,则△AOB
的面积为 .
“健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的
活动场地定在奥林匹克公园.所走路线如图所示:森林公园—玲珑
塔—国家体育场—水立方.若在奥林匹克公园设计图上玲珑塔的坐
标为(-1,0),森林公园的坐标为(-2,2),那么地图线不变时, 水
立方的坐标为 .
如图,已知一个长方形的长为8,宽为4,请建立适当的直角坐标
系,并求出A,B,C,D四点的坐标.
某台阶的一部分(每级台阶的高度和宽度相等)如图所示,如果点A的坐标为(0,0),点B
的坐标为(1,1).
(1)请建立适当的直角坐标系,并写出点C,D,E,F的坐标.
(2)如果该台阶有10级,你能得到该台阶的高度吗?
二、能力进阶
11.如图,在直角坐标系中,∠AOB=150°,OA=OB=2,则点
A的坐标是( )
A.(-1,) B.(-,1)
C.(-1,1) D.(-,)
12.已知点P(2m+3,3m-1)在第一、三象限的角平分线上,则点P的坐标为( )
A.(4,4) B.(3,3) C.(11,11) D.(-11,-11)
13.如图,在直角坐标系中,△OBC的顶点O与坐标原点重合,点B的坐标为(-6,),OC=15,BC=17,求线段OB的长度和△OBC的面积.
三、自我挑战
14.在直角坐标系中,A,B,C三点的坐标分别是A(5,0),B(0,3),C(5,3),O为坐标原点,点E在线段BC上.若△AEO为等腰三角形,求点E的坐标.
【参考答案】
1.B
2.A
3.D
4.A
5.D
6.C
7.2 .
8. (-2,-4)
9.解:如图,以C为原点,直线CB为x轴,直线CD为y轴建立直角坐标系.则A(8,4),B(8,0),C(0,0),D(0,4).(答案不唯一)
第9题答图
10.解:(1)如图,以点A为原点,水平方向为x轴,竖直方向为y轴建立直角坐标系.
∴点C,D,E,F的坐标分别为C(2,2),D(3,3),E(4,4),F(5,5).
(2)∵每级台阶高为1,∴10级台阶的高度是10.
B
C
13.解:如图,过点B作BM⊥x轴于点M.
∵点B的坐标为(-6,),
∴OM=6,BM=.
由勾股定理得
OB2=OM2+BM2=62+()2=64,
∴OB=8.
又∵OC=15,BC=17,
∴OB2+OC2=BC2,
∴△OBC是直角三角形,且∠BOC=90°,
∴S△OBC=×8×15=60.
14.解:如图所示.
若A为顶角顶点,则AE1=AO,故点E1(1,3);
若E为顶角顶点,则E2O=E2A,故点E2(2.5,3);
若O为顶角顶点,则OE3=OA,故点E3(4,3).
综上所述,点E的坐标为(1,3)或(2.5,3)或(4,3).
第5题
第8题
第11题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
