【浙教版】九年级下:1.3解直角三角形课件
文档属性
| 名称 | 【浙教版】九年级下:1.3解直角三角形课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-05 00:00:00 | ||
图片预览




文档简介
课件18张PPT。1.3 解直角三角形
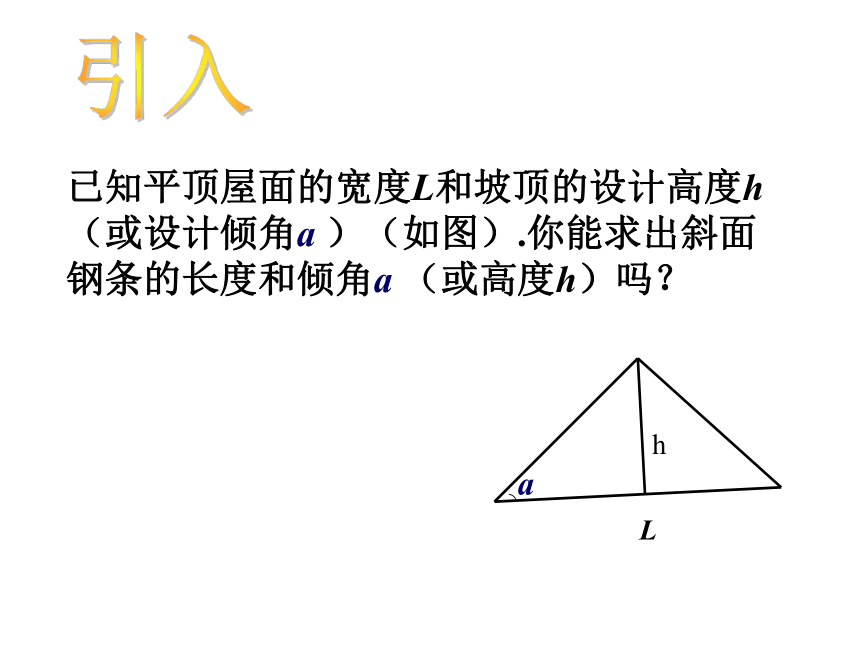
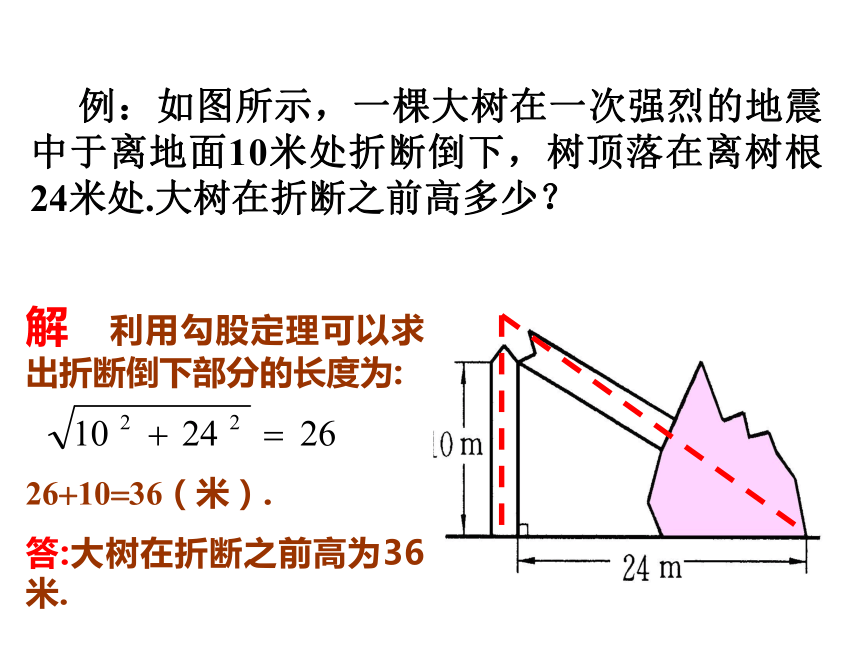
浙教版九年级(下册)已知平顶屋面的宽度L和坡顶的设计高度h(或设计倾角a )(如图).你能求出斜面钢条的长度和倾角a (或高度h)吗?引入hLa 例:如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.在例题中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样:
********************************
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系A+B=90°a2+b2=c2例1:如图1-16,在Rt△ABC中,∠C=90°,∠A=50 °,AB=3.
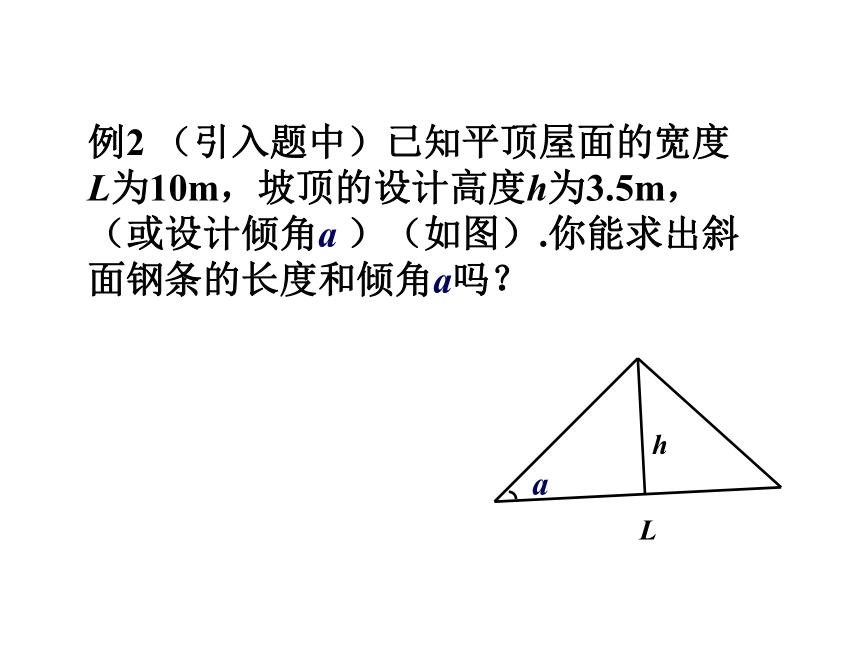
求∠B和a,b(边长保留2个有效数字)3ABCab例2 (引入题中)已知平顶屋面的宽度L为10m,坡顶的设计高度h为3.5m,(或设计倾角a )(如图).你能求出斜面钢条的长度和倾角a吗?hLa练习 如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)解:在Rt△ABC中,因为
∠CAB=90゜-∠DAC=50゜, =tan∠CAB,
所以BC=AB?tan∠CAB=2000×tan50゜
≈2384(米).
又因为
所以
AC=
答:敌舰与A、B两炮台的距离
分别约为3111米和2384米. 在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外, 边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
?
灯塔上发现在它的南偏东30°,距离500m的A处有一艘船,该船向正西方向航行,经过3分钟到达灯塔西北方向的B处,求这船的航速是每时多少千米( 取1.7) 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30°,求飞机A到控制点B距离 .
A1200米BC 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30°,求飞机A到控制点B距离 .仰角俯角铅垂线水平线仰角:在视线与水平线所形成的角中,视线在水平线上方的角.俯角:在视线与水平线所形成的角中,视线在水平线下方的角. 两大楼的水平距离为30米,从高楼的顶部A点测得低楼的顶部D点的俯角为45°,测得低楼的底部C点的俯角为60°,求两楼的高度.ADBC30米45°60°探索研究 大家都动起来 某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°,求铁塔AB高.(精确到0. 1米)330米ABCDEα︶探索研究 如图,在△ABC中, ∠ A为锐角,sin A= ,AB+AC=6cm,设AC=xcm, △ABC的面积为ycm2.
(1)求y关于x的函数关系式和自变量x的取值范围;
(2)何时△ABC的面积最大,最大面积为多少?当三角形变成平行四边形时,平行四边形的两邻边分别为a、b,这组邻边所夹的锐角为r时,则它的面积能否用这三个已知量来表示呢?S= ab sin A小结你会了吗? 1.弄清俯角、仰角、方位角等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题
2.认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题.
3.选择合适的边角关系式,使计算尽可能简单,且不易出错.
4.按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位.
ABC45°60°1002米D问题:一人在塔底A处测得塔顶C的仰角为45°,此人向塔前100米到B处,又测得塔顶的仰角为60°,已知测角器的高度为2米,求塔高.
浙教版九年级(下册)已知平顶屋面的宽度L和坡顶的设计高度h(或设计倾角a )(如图).你能求出斜面钢条的长度和倾角a (或高度h)吗?引入hLa 例:如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?解 利用勾股定理可以求出折断倒下部分的长度为:
26+10=36(米).
答:大树在折断之前高为36米.在例题中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角.像这样:
********************************
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
解直角三角形1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系A+B=90°a2+b2=c2例1:如图1-16,在Rt△ABC中,∠C=90°,∠A=50 °,AB=3.
求∠B和a,b(边长保留2个有效数字)3ABCab例2 (引入题中)已知平顶屋面的宽度L为10m,坡顶的设计高度h为3.5m,(或设计倾角a )(如图).你能求出斜面钢条的长度和倾角a吗?hLa练习 如图东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)解:在Rt△ABC中,因为
∠CAB=90゜-∠DAC=50゜, =tan∠CAB,
所以BC=AB?tan∠CAB=2000×tan50゜
≈2384(米).
又因为
所以
AC=
答:敌舰与A、B两炮台的距离
分别约为3111米和2384米. 在解直角三角形的过程中,常会遇到近似计算,本书除特别说明外, 边长保留四个有效数字,角度精确到1′.
解直角三角形,只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
?
灯塔上发现在它的南偏东30°,距离500m的A处有一艘船,该船向正西方向航行,经过3分钟到达灯塔西北方向的B处,求这船的航速是每时多少千米( 取1.7) 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30°,求飞机A到控制点B距离 .
A1200米BC 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=30°,求飞机A到控制点B距离 .仰角俯角铅垂线水平线仰角:在视线与水平线所形成的角中,视线在水平线上方的角.俯角:在视线与水平线所形成的角中,视线在水平线下方的角. 两大楼的水平距离为30米,从高楼的顶部A点测得低楼的顶部D点的俯角为45°,测得低楼的底部C点的俯角为60°,求两楼的高度.ADBC30米45°60°探索研究 大家都动起来 某高为5.48米的建筑物CD与一铁塔AB的水平距离BC为330米,一测绘员在建筑物顶点D测得塔顶A的仰角a为30°,求铁塔AB高.(精确到0. 1米)330米ABCDEα︶探索研究 如图,在△ABC中, ∠ A为锐角,sin A= ,AB+AC=6cm,设AC=xcm, △ABC的面积为ycm2.
(1)求y关于x的函数关系式和自变量x的取值范围;
(2)何时△ABC的面积最大,最大面积为多少?当三角形变成平行四边形时,平行四边形的两邻边分别为a、b,这组邻边所夹的锐角为r时,则它的面积能否用这三个已知量来表示呢?S= ab sin A小结你会了吗? 1.弄清俯角、仰角、方位角等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题
2.认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题.
3.选择合适的边角关系式,使计算尽可能简单,且不易出错.
4.按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位.
ABC45°60°1002米D问题:一人在塔底A处测得塔顶C的仰角为45°,此人向塔前100米到B处,又测得塔顶的仰角为60°,已知测角器的高度为2米,求塔高.
