6.4 线段的和差 教学课件(25张ppt)
文档属性
| 名称 | 6.4 线段的和差 教学课件(25张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 00:00:00 | ||
图片预览






文档简介
6.4 线段的和差
数学(浙教版)
七年级 上册
第6章 图形的初步认识
学习目标
1、理解线段中点和等分点的意义;
2、能够运用线段的和、差、倍、分关系求线段的长度;
3、学会利用分类讨论的思想方法求线段的长度;
温故知新
1、比较线段长短的方法:度量法和叠合法
2、用尺规作线段等于已知线段
3、基本实事:两点之间线段最短
4、两点之间的距离是连接两点的线段的长度
导入新课
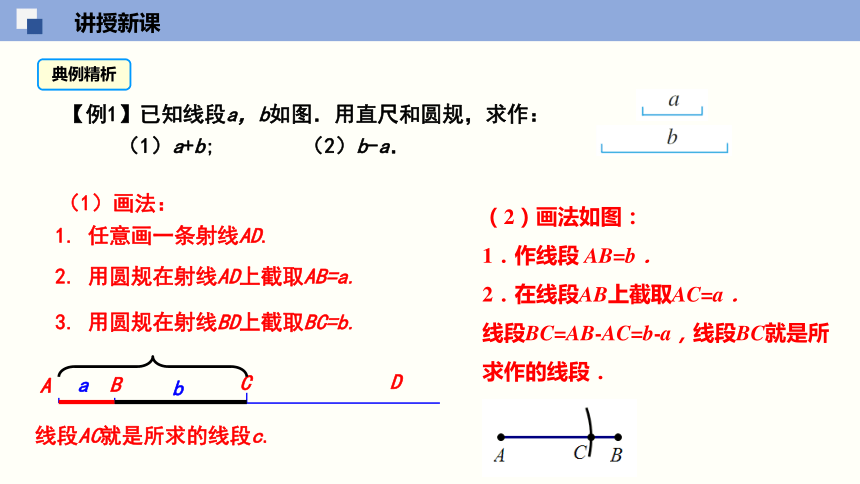
如图,从宾馆A出 发去景点B有A→C →B, A →D →B两条道路.你有哪些方法判别哪条路更近些?如果工具只有没有刻度的直尺和圆规呢?
讲授新课
知识点一 线段的和差
如图,已知线段a=1.5 cm,b=2.5 cm,c=4 cm.
请议一议,a,b,c三条线段的长度之间有怎样的关系?
a+b=1.5+2.5=4,所以a+b=c.
c-a=4-1.5=2.5,所以c-a=b.
c-b=4-2.5=1.5,所以c-b=a.
讲授新课
如果一条线段的长度是另两条线段的长度的和,那么这条线段就叫做另两条线段的和;如果一条线段的长度是另两条线段的长度的差,那么这条线段就叫做另两条线段的差.
两条线段的和或差仍是一条线段.
线段c是线段a与b的和,记做c=a+b;线段a是线段c与b的差,记做a=c-b.
概念归纳
讲授新课
典例精析
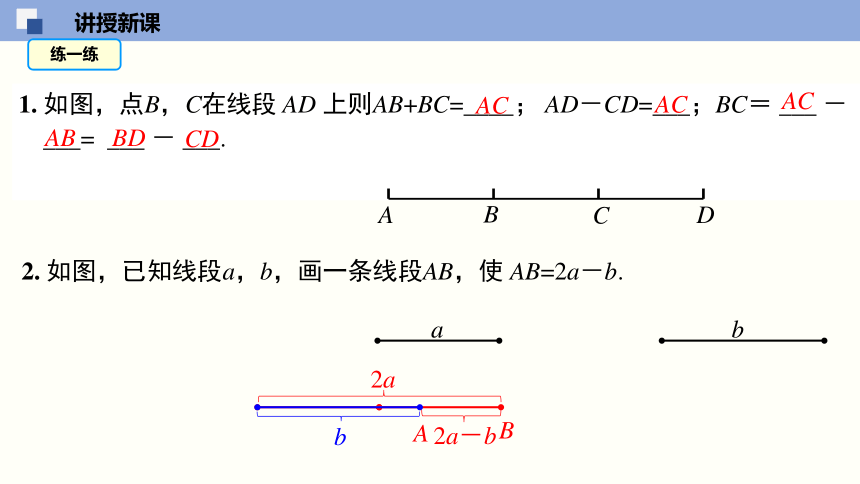
【例1】已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
b
(1)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC就是所求的线段c.
(2)画法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,线段BC就是所求作的线段.
讲授新课
【例2】如图,已知线段a,b,c,用直尺和圆规画线段,使得:
(1)AB=a-b;(2)OF=a-2b+c.
【解】 (1)画法:①画射线AM;
②在射线AM上截取AB=a,在线段AB的反方向截取BC=b;
线段AC就是所求的线段a-b.如解图①.
(2)画法:①画射线ON;
②在射线ON上依次截取OD=a,DE=c;
③在线段OE的反方向截取EF=2b.
线段OF就是所求的线段a-2b+c.如解图②.
讲授新课
练一练
1. 如图,点B,C在线段 AD 上则AB+BC=____; AD-CD=___;BC= ___ -___= ___ - ___.
A
B
C
D
AC
AC
AC
AB
BD
CD
2. 如图,已知线段a,b,画一条线段AB,使 AB=2a-b.
a
b
A
B
2a-b
2a
b
讲授新课
知识点二 线段的中点
利用尺规作图,我们可以作一条线段等于另一条线段的两倍,如图:AB=2AM.
A
B
M
根据作图可知:AM=MB,此时点M把线段AB分成了两条相等的线段.
把一条线段分成相等线段的点,叫做线段的中点.
A
B
M
如图,点M就是线段AB的中点.
讲授新课
思考:如图,若线段AB的中点是点M,你能得到哪些线段间的数量关系?
A
B
M
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
讲授新课
点 M , N 是线段 AB 的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
讲授新课
典例精析
【例3】如图,在直线上有A,B,C三点,AB= 4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:∵AB=4 cm,BC=3 cm,
∴ AC=AB+ BC=3+4=7 cm.
∵点O是线段AC的中点,
∴ OC= AC= 7 × =3.5 cm.
∴ OB=OC-BC=3.5-3=0.5(cm).
讲授新课
(1) 逐段计算:求线段的长度,主要围绕线段的和、差、倍、分关系展开.若每一条线段的长度均已确定,所求问题可迎刃而解.
计算线段长度的一般方法:
归纳总结
(2) 整体转化:巧妙转化是解题关键.首先将线段转化为两条线段的和,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.
讲授新课
练一练
1、若 AB = 6cm,点 C 是线段 AB 的中点,点 D是线段 CB 的中点,求:线段 AD 的长是多少?
解:∵ C 是线段 AB 的中点,
∵ D 是线段 CB 的中点,
∴ AC = CB = AB = ×6= 3 (cm).
∴ CD = CB = ×3=1.5 (cm).
∴ AD =AC + CD = 3 + 1.5 = 4.5 (cm).
A C B
D
讲授新课
解:∵点P是线段AB的中点,
∴AP=BP= AB.
∵点C,D把线段AB三等分,
∴AC=CD=DB= AB.
∴ AB- AB=CP,即CP = AB .
∴AB=6CP=6×1.5=9(cm) .
答:线段AB的长为9 cm.
2、如图,P是线段AB的中点,点C,D把线段AB三等分.已知线段CP的长为1.5 cm,求线段AB的长.
当堂检测
1.下列说法不正确的是( )
A.若点C在线段BA的延长线上,则BA=AC-BC
B.若点C在线段AB上,则AB=AC+BC
C.若AC+BC>AB,则点C一定在线段AB外
D.若A,B,C三点不在同一条直线上,则AB2.如果线段AB=13 cm,MA+MB=17 cm,那么下列说法正确的是( )
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可以在直线AB上,也可以在直线AB外
A
D
当堂检测
3、 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
【分析】分以下两种情况进行讨论:?当点C在AB之间上,故AC=AB-BC=1cm;?当点C在AB的延长线上时,AC=AB+BC=9cm.
C
【点睛】无图时求线段的长,应注意分类讨论,一般分以下两种情况:1.点在某一线段上;2.点在该线段的延长线.
当堂检测
4.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的 是( )
A.两点确定一条直线
B.两点之间,直线最短
C.两点之间,线段最短
D.两点之间,射线最短
C
当堂检测
5.如图,C,D,E是线段AB上的三个点,下面关于线段CE的表示:
①CE=CD+DE; ②CE=BC﹣EB;
③CE=CD+BD﹣AC; ④CE=AE+BC﹣AB.
其中正确的是 (填序号).
①②④
当堂检测
6.如图,B,C两点把线段AD分成2∶4∶3三部分,M是AD的中点,CD=6,求线段MC的长.
解:AB=6÷3×2=4,BC=6÷3×4=8,AD=AB+BC+CD=18,因为M是AD的中点,所以MD= AD=9,MC=MD-CD=3
当堂检测
7.如图,已知线段AB和CD的公共部分BD= AB= CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
F
E
B
D
C
A
【分析】根据已知条件,不妨设BD=xcm,则AB=3xcm,CD=4xcm,易得AC=
6xcm.在由线段中点的定义及线段的和差关系,用含x的代数式表示EF的长,从而得到一个一元一次方程,求解即可.
当堂检测
解:设BD=xcm,则AB=3xcm,CD=4xcm,AC =6xcm,
因为E、F分别是AB、CD的中点,
所以
所以EF=AC-AE-CF=
所以AB=3xcm=12cm,CD=4xcm=16cm.
F
E
B
D
C
A
因为EF=10,所以 x=10,解得x=4.
课堂小结
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
谢 谢~
数学(浙教版)
七年级 上册
第6章 图形的初步认识
学习目标
1、理解线段中点和等分点的意义;
2、能够运用线段的和、差、倍、分关系求线段的长度;
3、学会利用分类讨论的思想方法求线段的长度;
温故知新
1、比较线段长短的方法:度量法和叠合法
2、用尺规作线段等于已知线段
3、基本实事:两点之间线段最短
4、两点之间的距离是连接两点的线段的长度
导入新课
如图,从宾馆A出 发去景点B有A→C →B, A →D →B两条道路.你有哪些方法判别哪条路更近些?如果工具只有没有刻度的直尺和圆规呢?
讲授新课
知识点一 线段的和差
如图,已知线段a=1.5 cm,b=2.5 cm,c=4 cm.
请议一议,a,b,c三条线段的长度之间有怎样的关系?
a+b=1.5+2.5=4,所以a+b=c.
c-a=4-1.5=2.5,所以c-a=b.
c-b=4-2.5=1.5,所以c-b=a.
讲授新课
如果一条线段的长度是另两条线段的长度的和,那么这条线段就叫做另两条线段的和;如果一条线段的长度是另两条线段的长度的差,那么这条线段就叫做另两条线段的差.
两条线段的和或差仍是一条线段.
线段c是线段a与b的和,记做c=a+b;线段a是线段c与b的差,记做a=c-b.
概念归纳
讲授新课
典例精析
【例1】已知线段a,b如图.用直尺和圆规,求作:
(1)a+b; (2)b-a.
b
(1)画法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC就是所求的线段c.
(2)画法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,线段BC就是所求作的线段.
讲授新课
【例2】如图,已知线段a,b,c,用直尺和圆规画线段,使得:
(1)AB=a-b;(2)OF=a-2b+c.
【解】 (1)画法:①画射线AM;
②在射线AM上截取AB=a,在线段AB的反方向截取BC=b;
线段AC就是所求的线段a-b.如解图①.
(2)画法:①画射线ON;
②在射线ON上依次截取OD=a,DE=c;
③在线段OE的反方向截取EF=2b.
线段OF就是所求的线段a-2b+c.如解图②.
讲授新课
练一练
1. 如图,点B,C在线段 AD 上则AB+BC=____; AD-CD=___;BC= ___ -___= ___ - ___.
A
B
C
D
AC
AC
AC
AB
BD
CD
2. 如图,已知线段a,b,画一条线段AB,使 AB=2a-b.
a
b
A
B
2a-b
2a
b
讲授新课
知识点二 线段的中点
利用尺规作图,我们可以作一条线段等于另一条线段的两倍,如图:AB=2AM.
A
B
M
根据作图可知:AM=MB,此时点M把线段AB分成了两条相等的线段.
把一条线段分成相等线段的点,叫做线段的中点.
A
B
M
如图,点M就是线段AB的中点.
讲授新课
思考:如图,若线段AB的中点是点M,你能得到哪些线段间的数量关系?
A
B
M
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
讲授新课
点 M , N 是线段 AB 的三等分点:
AM = MN = NB = ___ AB
(或 AB = ___AM = ___ MN = ___NB)
3
3
3
N
M
B
A
讲授新课
典例精析
【例3】如图,在直线上有A,B,C三点,AB= 4 cm,BC=3 cm,如果O是线段AC的中点,求线段OB的长度.
解:∵AB=4 cm,BC=3 cm,
∴ AC=AB+ BC=3+4=7 cm.
∵点O是线段AC的中点,
∴ OC= AC= 7 × =3.5 cm.
∴ OB=OC-BC=3.5-3=0.5(cm).
讲授新课
(1) 逐段计算:求线段的长度,主要围绕线段的和、差、倍、分关系展开.若每一条线段的长度均已确定,所求问题可迎刃而解.
计算线段长度的一般方法:
归纳总结
(2) 整体转化:巧妙转化是解题关键.首先将线段转化为两条线段的和,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.
讲授新课
练一练
1、若 AB = 6cm,点 C 是线段 AB 的中点,点 D是线段 CB 的中点,求:线段 AD 的长是多少?
解:∵ C 是线段 AB 的中点,
∵ D 是线段 CB 的中点,
∴ AC = CB = AB = ×6= 3 (cm).
∴ CD = CB = ×3=1.5 (cm).
∴ AD =AC + CD = 3 + 1.5 = 4.5 (cm).
A C B
D
讲授新课
解:∵点P是线段AB的中点,
∴AP=BP= AB.
∵点C,D把线段AB三等分,
∴AC=CD=DB= AB.
∴ AB- AB=CP,即CP = AB .
∴AB=6CP=6×1.5=9(cm) .
答:线段AB的长为9 cm.
2、如图,P是线段AB的中点,点C,D把线段AB三等分.已知线段CP的长为1.5 cm,求线段AB的长.
当堂检测
1.下列说法不正确的是( )
A.若点C在线段BA的延长线上,则BA=AC-BC
B.若点C在线段AB上,则AB=AC+BC
C.若AC+BC>AB,则点C一定在线段AB外
D.若A,B,C三点不在同一条直线上,则AB
A.点M在线段AB上
B.点M在直线AB上
C.点M在直线AB外
D.点M可以在直线AB上,也可以在直线AB外
A
D
当堂检测
3、 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
【分析】分以下两种情况进行讨论:?当点C在AB之间上,故AC=AB-BC=1cm;?当点C在AB的延长线上时,AC=AB+BC=9cm.
C
【点睛】无图时求线段的长,应注意分类讨论,一般分以下两种情况:1.点在某一线段上;2.点在该线段的延长线.
当堂检测
4.把一条弯曲的公路改成直道,可以缩短路程,用几何知识解释其道理正确的 是( )
A.两点确定一条直线
B.两点之间,直线最短
C.两点之间,线段最短
D.两点之间,射线最短
C
当堂检测
5.如图,C,D,E是线段AB上的三个点,下面关于线段CE的表示:
①CE=CD+DE; ②CE=BC﹣EB;
③CE=CD+BD﹣AC; ④CE=AE+BC﹣AB.
其中正确的是 (填序号).
①②④
当堂检测
6.如图,B,C两点把线段AD分成2∶4∶3三部分,M是AD的中点,CD=6,求线段MC的长.
解:AB=6÷3×2=4,BC=6÷3×4=8,AD=AB+BC+CD=18,因为M是AD的中点,所以MD= AD=9,MC=MD-CD=3
当堂检测
7.如图,已知线段AB和CD的公共部分BD= AB= CD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
F
E
B
D
C
A
【分析】根据已知条件,不妨设BD=xcm,则AB=3xcm,CD=4xcm,易得AC=
6xcm.在由线段中点的定义及线段的和差关系,用含x的代数式表示EF的长,从而得到一个一元一次方程,求解即可.
当堂检测
解:设BD=xcm,则AB=3xcm,CD=4xcm,AC =6xcm,
因为E、F分别是AB、CD的中点,
所以
所以EF=AC-AE-CF=
所以AB=3xcm=12cm,CD=4xcm=16cm.
F
E
B
D
C
A
因为EF=10,所以 x=10,解得x=4.
课堂小结
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 AB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
谢 谢~
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
