6.8 余角和补角 课件 33张ppt

6.8 余角和补角
数学（浙教版）
七年级 上册
第6章 图形的初步认识
学习目标
1、了解余角、补角的概念，掌握余角和补角的性质；
2、能利用余角、补角的知识解决相关问题；
3、了解方位角的概念，并能用方位角知识解决一些简单的实际问题；
　
温故知新
1、角的和差及表示方法．
2、用量角器画一个角等于已知角．
3、角平分线：从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线．
4、与角平分线有关的角的计算．
O
B
A
C
　
导入新课
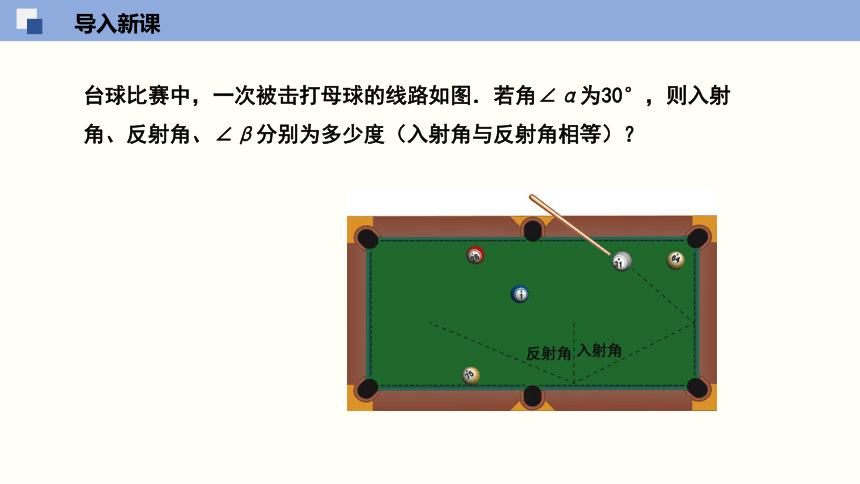
台球比赛中，一次被击打母球的线路如图．若角∠α为30°，则入射角、反射角、∠β分别为多少度（入射角与反射角相等）？
讲授新课
知识点一 认识余角和补角
在一副三角尺中，每块都有一个角是90o，而其他两个角的和是多少呢？
1
2
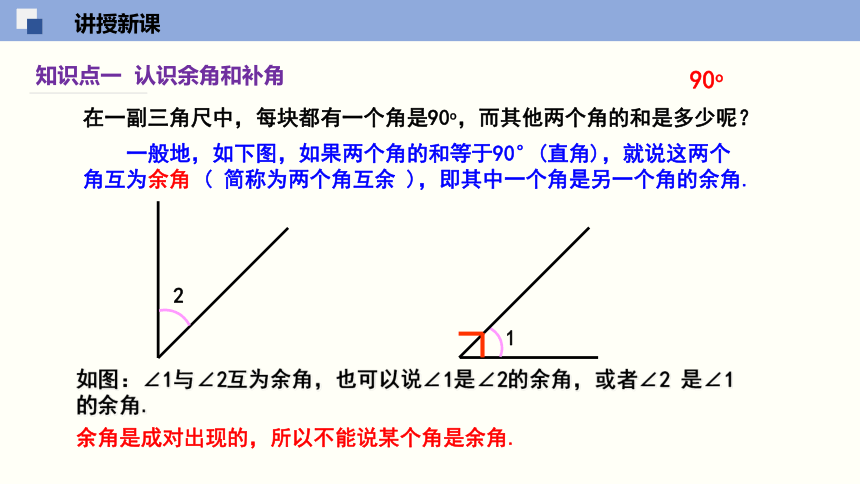
如图：∠1与∠2互为余角，也可以说∠1是∠2的余角，或者∠2 是∠1的余角.
余角是成对出现的，所以不能说某个角是余角.
一般地，如下图，如果两个角的和等于90°(直角)，就说这两个角互为余角 ( 简称为两个角互余 )，即其中一个角是另一个角的余角.
90o
讲授新课
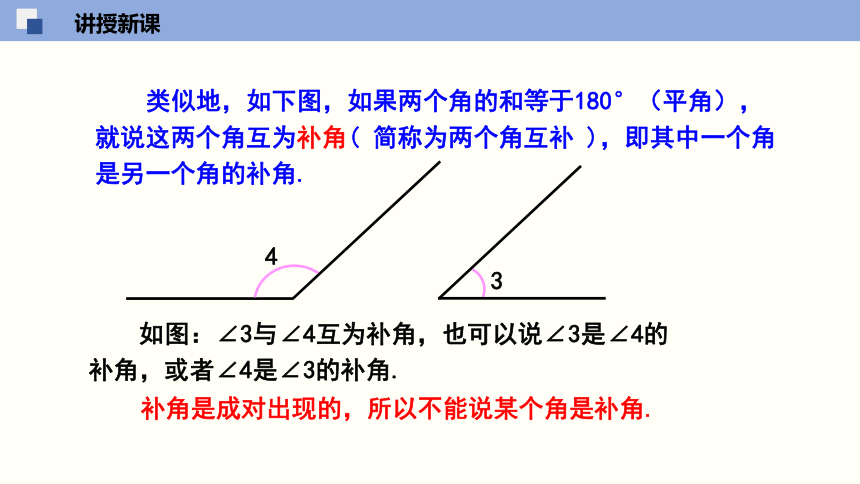
类似地，如下图，如果两个角的和等于180°（平角），就说这两个角互为补角( 简称为两个角互补 )，即其中一个角是另一个角的补角.
补角是成对出现的，所以不能说某个角是补角.
如图：∠3与∠4互为补角，也可以说∠3是∠4的补角，或者∠4是∠3的补角.
4
3
讲授新课
概念总结
余角的概念
1
如果两个角的和等于90°( 直角 )，就说这两个角互为余角 ( 简称为两个角互余 ).
如图，可以说 ∠1 是 ∠2 的余角，或 ∠2 是∠1的余角，或 ∠1和 ∠2互余.
2
讲授新课
概念总结
补角的概念
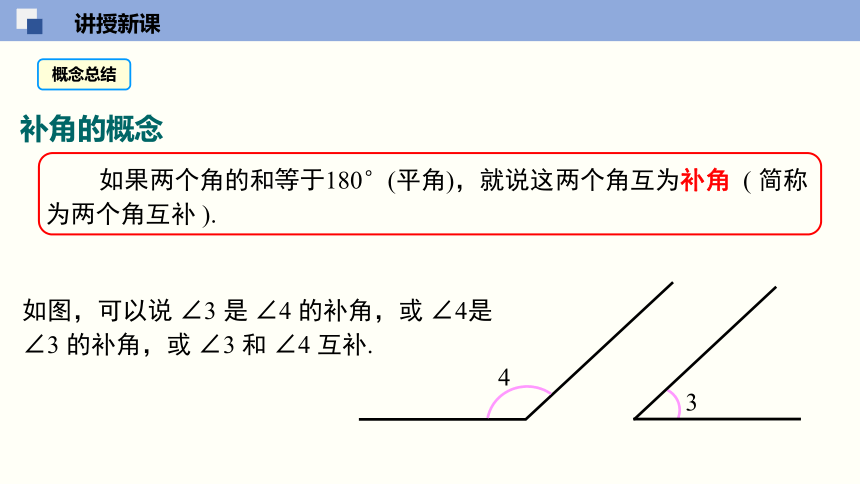
如果两个角的和等于180°(平角)，就说这两个角互为补角 ( 简称为两个角互补 ).
如图，可以说 ∠3 是 ∠4 的补角，或 ∠4是 ∠3 的补角，或 ∠3 和 ∠4 互补.
4
3
讲授新课
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}概念
定义
数量关系
共同点
互为余角
（互余）
互为补交
（互补）
如果两个锐角的和是一个直角，我们就说这两个角互为余角，也可以说其中一个角是另一个角的余角.
如果两个角的和是一个平角，我们就说这两个角互为补角，也可以说其中一个角是另一个角的补角.
①互余、互补是两个角的关系；
②互余、互补只跟角的大小有关，与位置无关.
讲授新课
典例精析
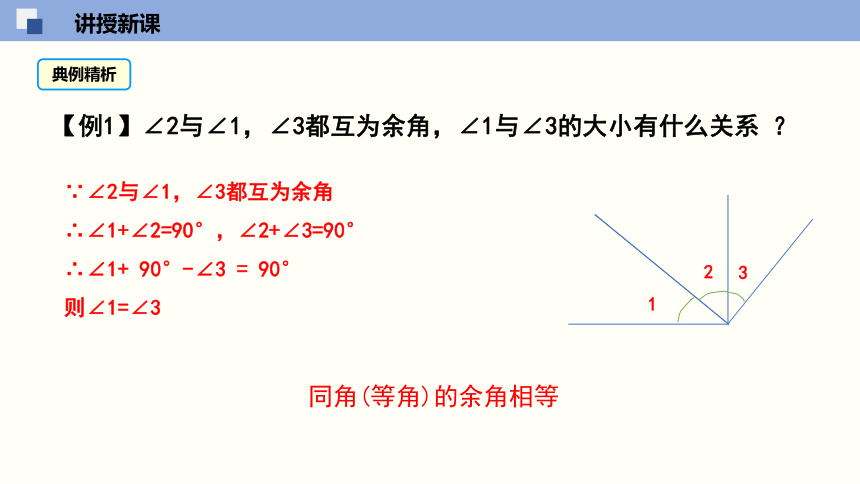
【例1】∠2与∠1，∠3都互为余角，∠1与∠3的大小有什么关系 ？
1
2
3
∵∠2与∠1，∠3都互为余角
∴∠1+∠2=90°，∠2+∠3=90°
∴∠1+ 90°-∠3 = 90°
则∠1=∠3
同角(等角)的余角相等
讲授新课
【例2】∠2与∠1，∠3都互为补角，∠1与∠3的大小有什么关系 ？
3
∵∠2与∠1，∠3都互为补角
∴∠1+∠2=180°,∠2+∠3=180°
∴∠1+180°-∠3=180°
则∠1=∠3
同角(等角)的补角相等
1
2
讲授新课
练一练
1.已知∠α是锐角，则∠α的余角可表示为__________，
∠α的补角可表示为 .
2.若∠α的余角是它的3倍，则∠α= .
3.若∠α的补角是它的4倍，则∠α= .
4.若∠α的补角是它的3倍，则 ∠α的余角为 .
90°-∠α
180°-∠α
22.5°
36°
45°
讲授新课
知识点二 余角、补角的性质
思考 ∠1 与∠2，∠3都互为补角，∠2 与∠3 的大小有什么关系？
1
2
同角 (等角) 的余角相等.
3
∠2=180°-∠1
∠3=180°-∠1
=
结论：
同角 (等角) 的补角相等.
类似地，可以得到：
讲授新课
同角 (等角) 的余角相等.
同角 (等角) 的补角相等.
几何语言：
∵∠1 +∠2=180°，∠1 +∠3=180°
∴∠2 =∠3
几何语言：
∵∠1 +∠2=90°，∠1 +∠3=90°
∴∠2 =∠3
讲授新课
典例精析
【例3】如图，点A，O，B在同一直线上，射线OD和射线OE 分别平分∠AOC 和∠BOC，图中哪些角互为余角？
O
A
B
C
D
E
解：因为点A，O，B在同一直线上，
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC 和∠BOC，
所以∠COD+∠COE= ∠AOC+ ∠BOC
= (∠AOC+∠BOC )= 90°.
所以∠COD和∠COE互为余角，
同理∠AOD和∠BOE，∠AOD和∠COE，∠COD和∠BOE也互为余角.
讲授新课
练一练
1．已知∠α与∠β互补，∠α=150°，则∠β的余角的度数是（ ）
A．30° B．60° C．45° D．90°
【详解】解：∵∠α与∠β互补，且∠α=150°，
∴∠β=180°-150°=30°，
∴∠β的余角=90??30?=60? 故选：B．
?
2．一个角的补角是这个角的余角的4倍，那么这个角的大小是（　　）
A．60° B．75° C．90° D．45°
【详解】解：设这个角为x，则补角为180°-x，余角为90°-x，
由题意得，180°-x=4（90°-x），
解得：x=60°．故选：A．
讲授新课
2、如图，O为直线AB上一点，OD平分∠AOC，∠DOE=90°．
（1）∠AOD的余角是______________，∠COD的余角是_______________;
（2 ）OE是∠BOC的平分线吗？请说明理由．
∠COE、∠BOE
O
A
B
C
D
E
∠COE、∠BOE
解：OE平分∠BOC
理由如下：∵∠DOE=90°，∴∠AOD+∠BOE=90°，
∴∠COD+∠COE=90°，
∴∠AOD+∠BOE=∠COD+∠COE，
∵OD平分∠AOC∴∠AOD=∠COD，
∴∠COE=∠BOE，∴OE平分∠BOC．
讲授新课
知识点三 方位角
东
西
北
南
O
正东：
正南：
正西：
正北：
西北方向：
西南方向：
东北方向：
东南方向：
射线 OA
A
B
C
D
45°
E
G
F
H
45°
八大方位
45°
45°
射线 OB
射线 OC
射线 OD
射线 OE
射线 OF
射线 OH
射线 OG
讲授新课
45°
如图，说出下列方位
(1) 射线 OA 表示的方向
为 .
(2) 射线 OB 表示的方向
为__________.
(3) 射线 OC 表示的方向
为 .
(4) 射线 OD 表示的方向
为 .
北
东
西
南
C
A
B
D
北偏东 40°
北偏西 65°
南偏西 45°(西南)
南偏东 20°
40°
65°
70°
O
20°
讲授新课
典例精析
【例4】如图，货轮O在航行过程中，发现灯塔A在它南偏东60°的方向上.同时，在它北偏东40°，南偏西10°，西北(即北偏西45°)方向上又分别发现了客轮B，货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B，货轮C和海岛D方向的射线.
东
南
西
北
60°
● B
40°
10°
45°
C ●
● A
● D
O
●
画法：1. 以点O为顶点，表示正北方的射线为角的一边，画40°的角，使它的另一边OB落在东与北之间. 射线OB的方向就是北偏东40°，即客轮B所在的方向.
2.同理画出射线OC、射线OD.
射线OC、射线OD即为所求.
讲授新课
练一练
1、如图,甲从点A出发向东偏南20°方向走50 m至点B,乙从A出发向南偏西15°方向走80 m至点C,则∠BAC的度数是( )
A.145°
B.85°
C.95°
D.75°
B
讲授新课
60°
30°
2. 垃圾打捞船 A 和 B 都停驻在湖边观测湖面，从A 船发现它的北偏东60°方向有白色漂浮物， 同时，从 B 船也发现该白色漂浮物在它的北偏西30°方向.
(1) 试在图中确定白色漂浮物C的位置；
A
B
北
北
C
讲授新课
60°
北
A. 南偏东30°
B. 南偏西30°
C. 南偏东60°
D. 南偏西60°
(2) 点 C 在点 A 的北偏东60°的方向上，那么点 A在点 C 的______方向上.
60°
30°
A
B
北
北
C
D
当堂检测
1．如果∠a=36°，那么∠a的余角等于（　　）
A．54° B．64° C．144° D．134°
解：∠a的余角=90°﹣∠α=90°﹣36°=54°．
故选A．
当堂检测
2．如图，AB、CD相交于点O，EO⊥AB，则∠1与∠2的关系是（　　）
A．相等 B．互余 C．互补 D．对顶角
解：∵EO⊥AB，
∴∠EOB=90°，
∵∠1+∠BOE+∠2=180°，
∴∠1+∠2=90°，
即∠1和∠2互余．故选B．
当堂检测
3．若∠A与∠B互为余角，则∠A+∠B=（　　）
A．180° B．120° C．90° D．60°
解：∵∠A与∠B互为余角，
∴∠A+∠B=90°，
故选：C．
当堂检测
4、已知一个角的补角是这个角的余角的4倍，求这个角的度数．
解:设这个角为x度，则这个角的余角是(90－x) 度，补角是(180－x)度，由题意得,
180－x=4(90－x)，
解得x=60，
答：这个角的度数为60°．
当堂检测
解：设∠2=x，则∠1=x+20，由题意得：∠1+∠2=x+20+x=180，
∴x=80°，
∴∠2=80°，∠1=x+20°=100°．
5.已知∠1与∠2互为补角，且∠1比∠2大20°，求∠1、∠2的度数．
当堂检测
6.如图，射线OA的方向是北偏东15°,射线OB的方向是北偏西40°，∠AOC=∠AOB ，射线OD 是OB 的反向延长线．
（1）射线OC的方向是__________；
（2）求∠AOD的度数；
（3）若射线OE平分∠COD,求∠AOE的度数．
解：（1）北偏东70°；
（2）∵∠AOB=55°，∠AOC=∠AOB，
∴∠BOC=110°.
又∵ 射线OD是OB的反向延长线，
∴∠BOD=180°.
∴∠COD=180°－110°=70°.
(3) ∵ ∠COD=70°， OE平分∠COD，
∴∠COE=35°.
∵∠AOC=55°.
∴∠AOE=90°
当堂检测
7. 如图，∠AOB＝160°，∠AOD与∠DOC互余，∠BOD＝90°，求∠COD的度数．
解：∵∠AOB＝160°，∠BOD＝90°，
∴∠AOD＝70°.
∵∠AOD与∠DOC互余，
∴∠AOD＋∠DOC＝90°.
∴∠COD＝90°－∠AOD＝90°－70°＝20°.
课堂小结
同角或等角的
补角相等
同角或等角的
余角相等
互余
互补
两角间的数量关系
对应图形
性质
课堂小结
方位角
物体运动的方向与正北、正南方向之间的夹角称为方位角，一般以正北、正南为基准，用向东或向西旋转的角度表示方向
定义
书写
通常要先写北或南，再写偏东或偏西
谢 谢~