2.1 直线与圆的位置关系(2) 课件(共20张PPT)
文档属性
| 名称 | 2.1 直线与圆的位置关系(2) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-21 11:17:02 | ||
图片预览





文档简介
(共20张PPT)
浙教版九年级下册
2.1 直线与圆的位置关系 (2)
第二章 直线与圆的位置关系
下雨天快速转动雨伞时飞出的水珠
在砂轮下打磨工件时飞出的火星
都是沿着圆的切线方向飞出的------
汽车轮胎与地面近似相切
∟
∟
∟
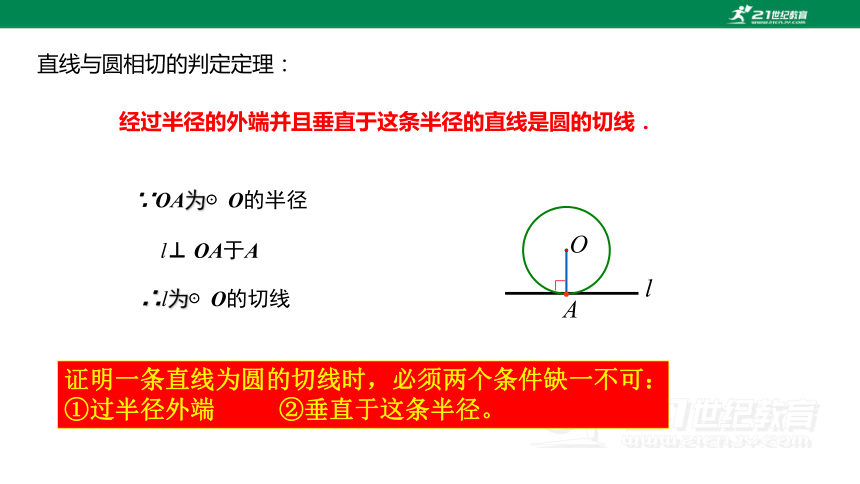
经过半径的外端并且垂直于这条半径的直线是圆的切线.
温故知新
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
什么是圆的切线?
如图,圆心O到直线l的距离OA等于圆O的半径,直线l是⊙O的切线
直线l的特征:(1)直线l经过半径OA的外端点A
(2)直线l垂直于半径OA 。
l
O
A
∟
经过半径的外端并且垂直于这条半径的直线是圆的切线.
∵OA为⊙O的半径
l⊥ OA于A
∴l为⊙O的切线
证明一条直线为圆的切线时,必须两个条件缺一不可: ①过半径外端 ②垂直于这条半径。
直线与圆相切的判定定理:
l
O
A
∟
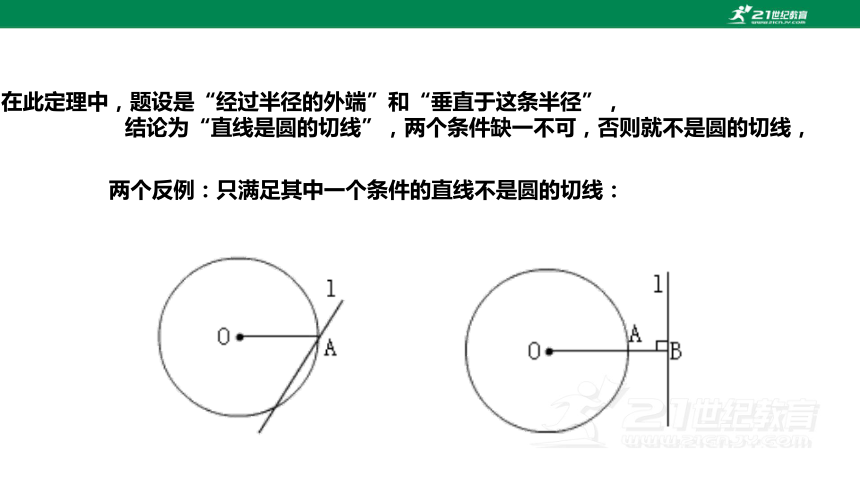
在此定理中,题设是“经过半径的外端”和“垂直于这条半径”,
结论为“直线是圆的切线”,两个条件缺一不可,否则就不是圆的切线,
两个反例:只满足其中一个条件的直线不是圆的切线:
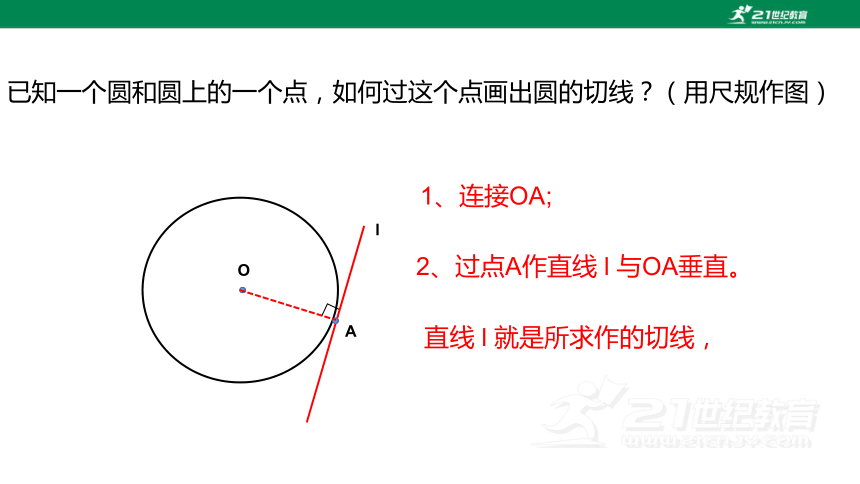
已知一个圆和圆上的一个点,如何过这个点画出圆的切线?(用尺规作图)
1、连接OA;
2、过点A作直线 l 与OA垂直。
直线 l 就是所求作的切线,
l
O
A
∟
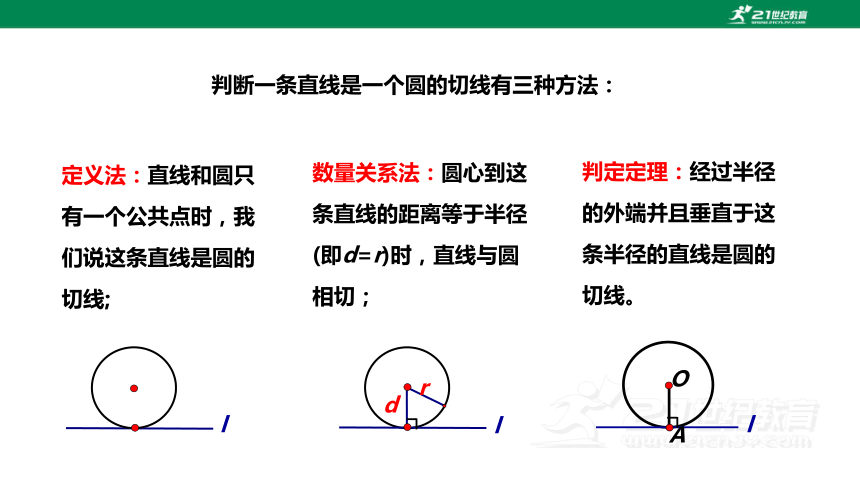
判断一条直线是一个圆的切线有三种方法:
定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
l
l
r
d
A
l
O
例3 已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,
点B在圆上,且AB=BC,∠A=30°.
求证:直线AB是⊙O的切线.
证明:连结OB.
∴∠OBC=∠C=∠A=30°,
∴∠AOB=∠C+∠OBC=60°.
∵∠ABO=180°-(∠AOB+∠A)=180°-(60°+30°)=90°,
∴AB⊥OB,
∴AB为⊙O的切线(经过半径的外端并且垂直这条半径的直线是圆的切线).
题目中“半径”已有,只需证“垂直”即可得直线与圆相切。
学以致用
例4:如图,台风中心P(100,200)沿北偏东30°方向移动,受台风影响区域的半径为200km.那么下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些受到这次台风的影响,哪些不受到这次台风的影响?
解:如图,在坐标系中画出以点P(100,200)为圆心,
以200为半径的⊙P,再在点P处画出北偏东30°
方向的方向线,作垂直于方向线的⊙P的直径HK,
分别过点H,K作⊙P的切线l1,l2,则l1∥l2.
因为台风圈在两条平行线l1,l2,之间移动,
点A,D落在切线l1,l2,之间,所以受到这次台风的影响;
而点B,C不在切线l1,l2,之间,
所以不受到这次台风的影响.
300
1.如图,将直角三角板的直角顶点B放在⊙O上,直角边AB经过圆心O,则另一直角边BC与⊙O的位置关系为( )
A.相交
B.相切
C.相离
D.无法确定
B
夯实基础,稳扎稳打
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
2.如图,AB是⊙O的直径 . 请分别过点A,B作⊙O的切线.
∟
∟
3.如图,点Q在⊙O上.分别根据下列条件,判定直线PQ与⊙O是否相切.
(1)OQ=6,OP=10,PQ=8.
解:∵OQ=6,OP=10,PQ=8,
∴OP2=OQ2+PQ2,∴∠OQP=90°.
∵点Q在⊙O上,∴OQ为⊙O的半径,∴PQ与⊙O相切.
(2)∠Q=67.3°,∠P=22°42 .
解:∵∠O=67.3°,∠P=22 ° 42 ,
∴∠Q+∠P=90°,∴∠OQP=90°.
∵Q在⊙O上,∴OQ为⊙O的半径.
∴OQ与⊙O相切.
4.如图,OP是⊙O的半径,∠POT=60°,OT交⊙O于点S.
(1)过点P作⊙O的切线.
(2)过点P的切线交OT于点Q,判断点S是不是线段OQ的中点,并说明理由.
.
解:(1)如图.
(2)点S是OQ的中点.
∵PQ为⊙O的切线,∴∠OPQ=90°.
∵∠POQ=60°,∴∠OQP=30°,
∴OQ=2PO.
∵PO=SO,∴OQ=2SO,
即点S是OQ的中点.
5.已知:如图,AB是⊙O的直径,BC⊥AB,弦AD∥OC.
求证:DC是⊙O的切线.
证明:如答图,连结OD.∵AD∥OC,
∴∠COB=∠A,∠ADO=∠DOC.
∵OA=OD,∴∠A=∠ADO,∴∠COB=∠DOC.
又∵OC=OC,OD=OB,
∴△CDO≌△CBO(SAS),
∴∠CDO=∠CBO=90°,
∴DC是⊙O的切线.
有交点,连半径,证垂直
连续递推,豁然开朗
6.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,3)
B.(2,4)
C.(1,4)
D.(6,2)
D
正方形+菱形+筝形-------
.
线段BC怎么称呼?
特殊四边形的对角线
7.如图,已知OA=OB=5,AB=8,⊙O的直径为6.
求证:AB与⊙O相切.
证明:过点O作OC⊥AB
∵OA=OB=5,AB=8
∴AC=BC=4
∴在Rt△AOC中,OC=3,
又∵⊙O的直径长为6,
∴OC=半径r
∴直线AB是⊙O的切线.
无交点,作垂直,证d=r
O
A
B
∟
C
8:当圆心到直线的距离等于圆的半径时,该直线是这个圆的切线
已知:⊙O的圆心O到直线l 的距 离等于⊙O的半径r。
A
求证:直线l 是⊙O的切线
证明:过点O作OA⊥l ,A为垂足。
∵OA=d=r
∴点A在⊙O上
∴OA是⊙O的半径
∴ l 是⊙O的切线
题目的条件中“垂直”和“距离等于半径”都没有明确显示出来,就必须先作出“垂直”,再证“距离等于半径”
9、如图⊙O的半径为8,弦AB= ,以O为圆心,4为半径作小圆,求证:AB与小圆O相切.
A
B
O
证明:过O作OC⊥AB于C,连结OA
∴AC=4 ,
.
∴点C在圆上
∵OC⊥AB
∴AB与小圆O相切
无交点,作垂直,证等于半径.
C
.
OC= =4
.
.
当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后证明直线与这条半径垂直,即可得出已知直线为圆的切线.
有交点,连半径,
证垂直;
当未提及直线与圆有公共点时,过圆心作直线的垂线,证明垂线段等于半径,即可得出已知直线为圆的切线.
无交点,作垂直,
证半径.
10.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E.弦BF交CD于点G,点P在CD延长线上,且PF=PG. 求证:PF为⊙O的切线.
证明:如图,连结OF.
∵PF=PG,∴∠PFG=∠PGF.
∵OB=OF,∴∠OBF=∠OFB.
∵CD⊥AB,∴∠GEB=90°.
∴∠ABF+∠EGB=90°.
∵∠EGB=∠PGF,∴∠OFB+∠PFG=90°.
∴∠PFO=90°,即OF⊥PF.∴PF为⊙O的切线.
浙教版九年级下册
2.1 直线与圆的位置关系 (2)
第二章 直线与圆的位置关系
下雨天快速转动雨伞时飞出的水珠
在砂轮下打磨工件时飞出的火星
都是沿着圆的切线方向飞出的------
汽车轮胎与地面近似相切
∟
∟
∟
经过半径的外端并且垂直于这条半径的直线是圆的切线.
温故知新
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
什么是圆的切线?
如图,圆心O到直线l的距离OA等于圆O的半径,直线l是⊙O的切线
直线l的特征:(1)直线l经过半径OA的外端点A
(2)直线l垂直于半径OA 。
l
O
A
∟
经过半径的外端并且垂直于这条半径的直线是圆的切线.
∵OA为⊙O的半径
l⊥ OA于A
∴l为⊙O的切线
证明一条直线为圆的切线时,必须两个条件缺一不可: ①过半径外端 ②垂直于这条半径。
直线与圆相切的判定定理:
l
O
A
∟
在此定理中,题设是“经过半径的外端”和“垂直于这条半径”,
结论为“直线是圆的切线”,两个条件缺一不可,否则就不是圆的切线,
两个反例:只满足其中一个条件的直线不是圆的切线:
已知一个圆和圆上的一个点,如何过这个点画出圆的切线?(用尺规作图)
1、连接OA;
2、过点A作直线 l 与OA垂直。
直线 l 就是所求作的切线,
l
O
A
∟
判断一条直线是一个圆的切线有三种方法:
定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
l
l
r
d
A
l
O
例3 已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,
点B在圆上,且AB=BC,∠A=30°.
求证:直线AB是⊙O的切线.
证明:连结OB.
∴∠OBC=∠C=∠A=30°,
∴∠AOB=∠C+∠OBC=60°.
∵∠ABO=180°-(∠AOB+∠A)=180°-(60°+30°)=90°,
∴AB⊥OB,
∴AB为⊙O的切线(经过半径的外端并且垂直这条半径的直线是圆的切线).
题目中“半径”已有,只需证“垂直”即可得直线与圆相切。
学以致用
例4:如图,台风中心P(100,200)沿北偏东30°方向移动,受台风影响区域的半径为200km.那么下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些受到这次台风的影响,哪些不受到这次台风的影响?
解:如图,在坐标系中画出以点P(100,200)为圆心,
以200为半径的⊙P,再在点P处画出北偏东30°
方向的方向线,作垂直于方向线的⊙P的直径HK,
分别过点H,K作⊙P的切线l1,l2,则l1∥l2.
因为台风圈在两条平行线l1,l2,之间移动,
点A,D落在切线l1,l2,之间,所以受到这次台风的影响;
而点B,C不在切线l1,l2,之间,
所以不受到这次台风的影响.
300
1.如图,将直角三角板的直角顶点B放在⊙O上,直角边AB经过圆心O,则另一直角边BC与⊙O的位置关系为( )
A.相交
B.相切
C.相离
D.无法确定
B
夯实基础,稳扎稳打
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
2.如图,AB是⊙O的直径 . 请分别过点A,B作⊙O的切线.
∟
∟
3.如图,点Q在⊙O上.分别根据下列条件,判定直线PQ与⊙O是否相切.
(1)OQ=6,OP=10,PQ=8.
解:∵OQ=6,OP=10,PQ=8,
∴OP2=OQ2+PQ2,∴∠OQP=90°.
∵点Q在⊙O上,∴OQ为⊙O的半径,∴PQ与⊙O相切.
(2)∠Q=67.3°,∠P=22°42 .
解:∵∠O=67.3°,∠P=22 ° 42 ,
∴∠Q+∠P=90°,∴∠OQP=90°.
∵Q在⊙O上,∴OQ为⊙O的半径.
∴OQ与⊙O相切.
4.如图,OP是⊙O的半径,∠POT=60°,OT交⊙O于点S.
(1)过点P作⊙O的切线.
(2)过点P的切线交OT于点Q,判断点S是不是线段OQ的中点,并说明理由.
.
解:(1)如图.
(2)点S是OQ的中点.
∵PQ为⊙O的切线,∴∠OPQ=90°.
∵∠POQ=60°,∴∠OQP=30°,
∴OQ=2PO.
∵PO=SO,∴OQ=2SO,
即点S是OQ的中点.
5.已知:如图,AB是⊙O的直径,BC⊥AB,弦AD∥OC.
求证:DC是⊙O的切线.
证明:如答图,连结OD.∵AD∥OC,
∴∠COB=∠A,∠ADO=∠DOC.
∵OA=OD,∴∠A=∠ADO,∴∠COB=∠DOC.
又∵OC=OC,OD=OB,
∴△CDO≌△CBO(SAS),
∴∠CDO=∠CBO=90°,
∴DC是⊙O的切线.
有交点,连半径,证垂直
连续递推,豁然开朗
6.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,3)
B.(2,4)
C.(1,4)
D.(6,2)
D
正方形+菱形+筝形-------
.
线段BC怎么称呼?
特殊四边形的对角线
7.如图,已知OA=OB=5,AB=8,⊙O的直径为6.
求证:AB与⊙O相切.
证明:过点O作OC⊥AB
∵OA=OB=5,AB=8
∴AC=BC=4
∴在Rt△AOC中,OC=3,
又∵⊙O的直径长为6,
∴OC=半径r
∴直线AB是⊙O的切线.
无交点,作垂直,证d=r
O
A
B
∟
C
8:当圆心到直线的距离等于圆的半径时,该直线是这个圆的切线
已知:⊙O的圆心O到直线l 的距 离等于⊙O的半径r。
A
求证:直线l 是⊙O的切线
证明:过点O作OA⊥l ,A为垂足。
∵OA=d=r
∴点A在⊙O上
∴OA是⊙O的半径
∴ l 是⊙O的切线
题目的条件中“垂直”和“距离等于半径”都没有明确显示出来,就必须先作出“垂直”,再证“距离等于半径”
9、如图⊙O的半径为8,弦AB= ,以O为圆心,4为半径作小圆,求证:AB与小圆O相切.
A
B
O
证明:过O作OC⊥AB于C,连结OA
∴AC=4 ,
.
∴点C在圆上
∵OC⊥AB
∴AB与小圆O相切
无交点,作垂直,证等于半径.
C
.
OC= =4
.
.
当已知直线过圆上的一点时,连接圆心和该点得到圆的半径,然后证明直线与这条半径垂直,即可得出已知直线为圆的切线.
有交点,连半径,
证垂直;
当未提及直线与圆有公共点时,过圆心作直线的垂线,证明垂线段等于半径,即可得出已知直线为圆的切线.
无交点,作垂直,
证半径.
10.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E.弦BF交CD于点G,点P在CD延长线上,且PF=PG. 求证:PF为⊙O的切线.
证明:如图,连结OF.
∵PF=PG,∴∠PFG=∠PGF.
∵OB=OF,∴∠OBF=∠OFB.
∵CD⊥AB,∴∠GEB=90°.
∴∠ABF+∠EGB=90°.
∵∠EGB=∠PGF,∴∠OFB+∠PFG=90°.
∴∠PFO=90°,即OF⊥PF.∴PF为⊙O的切线.
