6.1 矩形（1）

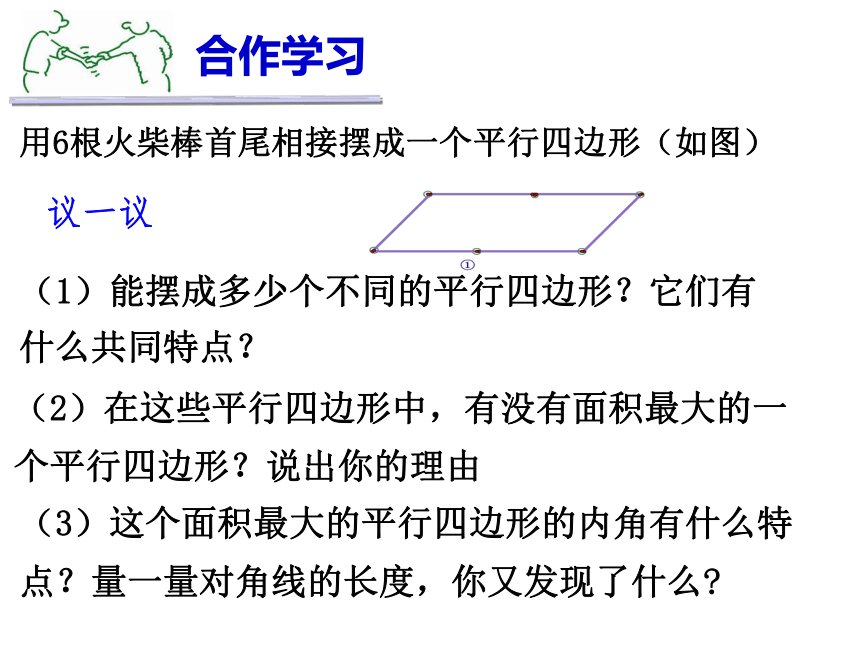
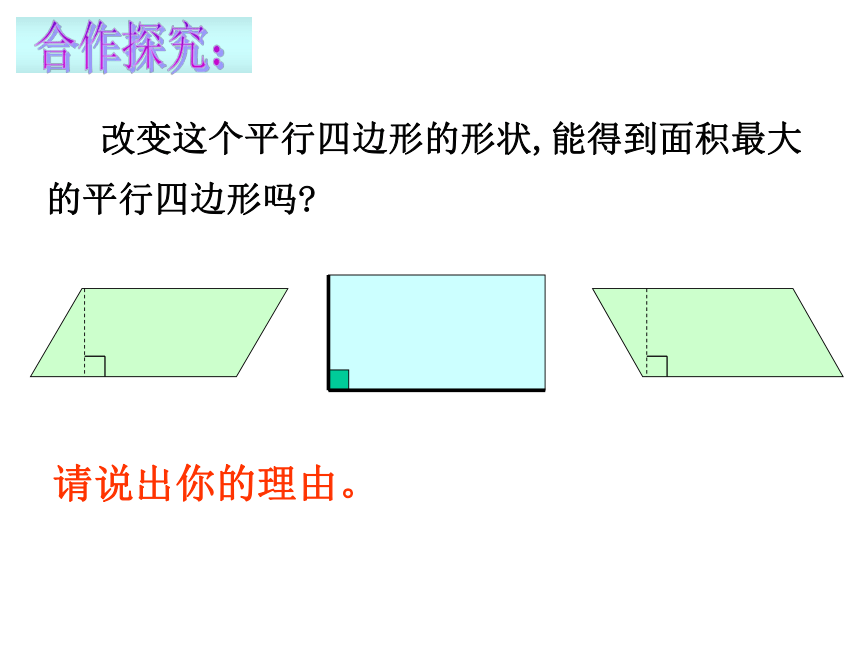
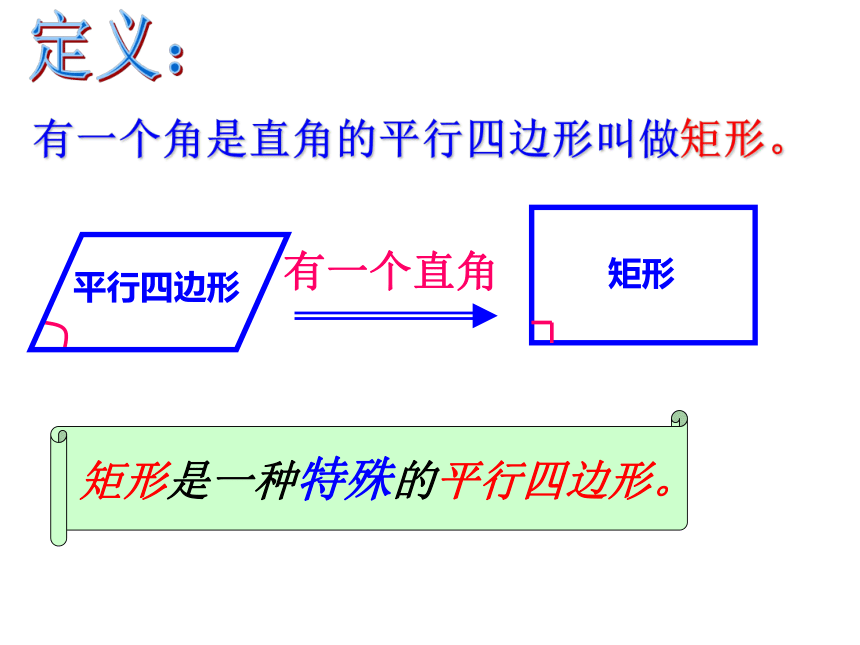
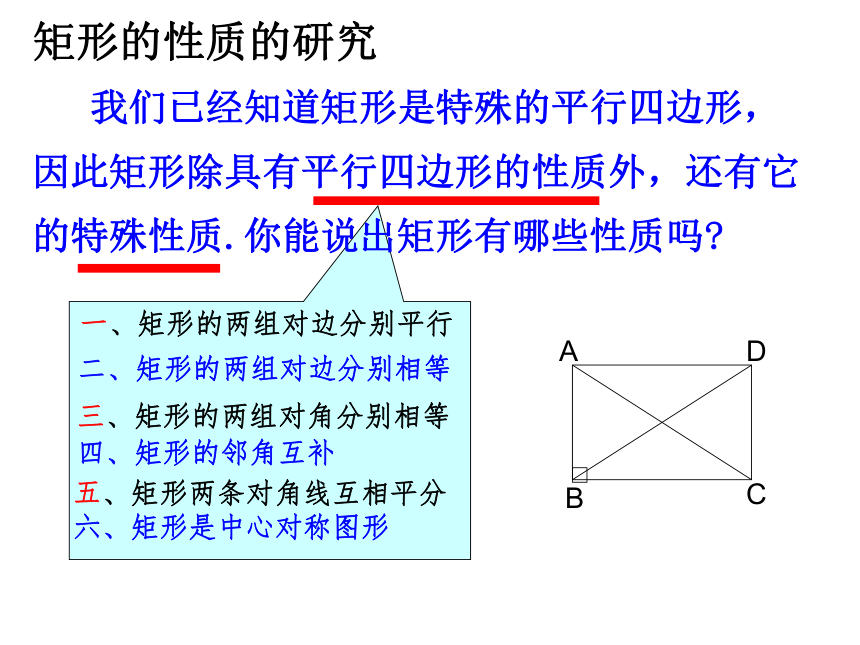
课件19张PPT。6.1矩形(1)温故知新平行四边形的性质（1）从边看（2）从角看（3）从对角线看（4）从对称看合作学习用6根火柴棒首尾相接摆成一个平行四边形（如图）（1）能摆成多少个不同的平行四边形？它们有什么共同特点？（2）在这些平行四边形中，有没有面积最大的一个平行四边形？说出你的理由（3）这个面积最大的平行四边形的内角有什么特点？量一量对角线的长度，你又发现了什么?议一议 改变这个平行四边形的形状,能得到面积最大的平行四边形吗? 合作探究：请说出你的理由。有一个角是直角的平行四边形叫做矩形。 定义：有一个直角矩形请看日常生活中的矩形矩形的性质的研究 我们已经知道矩形是特殊的平行四边形，因此矩形除具有平行四边形的性质外，还有它的特殊性质.你能说出矩形有哪些性质吗?五、矩形两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行四、矩形的邻角互补六、矩形是中心对称图形如图，四边形ABCD是矩形。O探索矩形特殊性质：(1)矩形的四个角的度数分别为多少？(2)对角线AC与BD间有什么关系？矩形的四个角都是直角。矩形的对角线相等如图：已知四边形ABCD是矩形,∠B=Rt∠。定理1 矩形的四个角都是直角。求证：∠A=∠B=∠C=∠D=Rt∠。矩形的特殊性质定理2 矩形的对角线相等已知：AC、BD是矩形ABCD的对角线。求证：AC=BD。证明：在矩形ABCD中，∵ AB=CD?CB=BC∴ Rt△ABC≌Rt△DCB(SAS)∴ AC=BD∠ABC=∠DCB=Rt∠（平行四边形的对边相等）（矩形的四个角都是直角）矩形的特殊性质定理1: 矩形的四个角都是直角∵矩形ABCD，
∴ ∠BAD＝∠CDA =∠BCD＝∠ABC ＝Rt∠定理2:矩形的对角线相等且互相平分． ∵ AC，BD是矩形ABCD的对角线
∴ AC＝BD,OA=OB=OC=OD.思考：对角线AC、BD相交于点O，图中有多少个等腰三角形？有多少对全等三角形？ABCDO矩形的对称性:矩形是中心对称图形,又是轴对称图形。矩形的对称中心在哪？矩形是对称轴有几条?例1、已知:矩形ABCD的两条对角线AC、BD相交于点0,
∠AOD=120°, AB = 4cm,
求（1）判断△AOB的形状；（2）矩形对角线的长.解:∵四边形ABCD是矩形
∴AC = BD( )矩形的对角线相等∴ OA= OB平行四边形的对角线互相平分∵∠AOD=120°
∴∠AOB=180°－∠AOD = 60°∴ △AOB 是等边三角形 ∴OA=OB=AB=4cm∴BD=AC = 2OA=8cm.你还能求出哪些量？1. 矩形具有而一般平行四边形不具有的性质是（ ）.A 对角线相等 B 对边相等 C 对角相等 D 对角线互相平分练一练C423.矩形ABCD中，已知AB=8㎝，AD=6㎝，则OB=____ ㎝，若已知∠CAB=40°，则 ∠OBA=____ ∠AOD=____540°80°4、如图，矩形ABCD的两条对角线相交于点O（1）△AOD是什么三角形？并说明理由.图中像这样的三角形共有几个，分别是？
（2）图中有多少对全等三角形？请把它们都写出来.练一练若要使∠AMD是直角，应增加什么条件？例2、求证：直角三角形斜边上的中线等于斜边的一半。已知：在△ABC中，∠ABC=Rt∠，OB是斜边的中线证明：延长BO到点D，使OD=OB，连结AD，CD∵ OA=OC，OD=OB∴四边形ABCD是平行四边形∵∠ABC=Rt∠∴四边形ABCD是矩形（有一个角是直角的平行四边形是矩形）推论：1、如图，在矩形ABCD中，E，F分别是AB，CD的中点.
求证：四边形AEFD是矩形做一做2.已知:如图,过矩形ABCD的顶点C作CE//BD，交AB的延长线于E。 求证：∠CAE=∠CEA1.一个定义：2.二个定理:3.二个结论:(1)矩形的两条对角线被交点分成的四条线段 相等(2)矩形既是轴对称图形，又是中心对称图形这节课你学到了什么? 还有什么困惑吗？再见!