第五章一次函数专题5.1 函数-重难点题型(含解析)
文档属性
| 名称 | 第五章一次函数专题5.1 函数-重难点题型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 16:22:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
函数6大题型
【知识点1 函数的概念】
一般地,在某一变化过程中有两个变量x与y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
注意:要判断一个关系式是不是函数,首先看这个变化过程中是否只有两个变量,其次看每一个x的值是否对应唯一确定的y值.
【知识点2 求函数的值】
(1)当已知函数解析式时,求函数值就是求代数式的值;函数值是唯一的,而对应的自变量可以是多个.(2)函数表达式中只有两个变量,给定一个变量的值,将其代入函数表达式即可求另一个变量的值,即给自变量的值可求函数值,给函数值可求自变量的值.
【题型1 常量与变量】
【例1】如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积ycm2与MA的长度xcm之间的关系式,并指出其中的常量与变量.
【变式1-1】.用同样大小的黑色棋子按如图所示的方式摆图形,按照这样的规律摆下去,则第n个图形的棋子数y= (用含n的代数式表示),其中变量是 .
【变式1-2】按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
【变式1-3】在烧开水时,水温达到100℃就会沸腾,下表是某同学做“观察水的沸腾”实验时记录的数据:
(1)上表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间推移2分钟,水的温度如何变化?
(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?
(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
【题型2 判断函数关系】
【例2】(2021春 海淀区期末)如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度h、水面的面积S及注水量V是三个变量.下列有四种说法:
①S是V的函数;②V是S的函数;③h是S的函数,④S是h的函数.
其中所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
【变式2-1】(2021春 开福区校级月考)下列式子中,y不是x的函数的是( )
A.y=x2 B.y=|x| C.y=2x+1 D.(x≥0)
【变式2-2】(2021春 邯郸期末)下列不能表示y是x的函数的是( )
A.
x 0 5 10 15
y 3 3.5 4 4.5
B.
C.
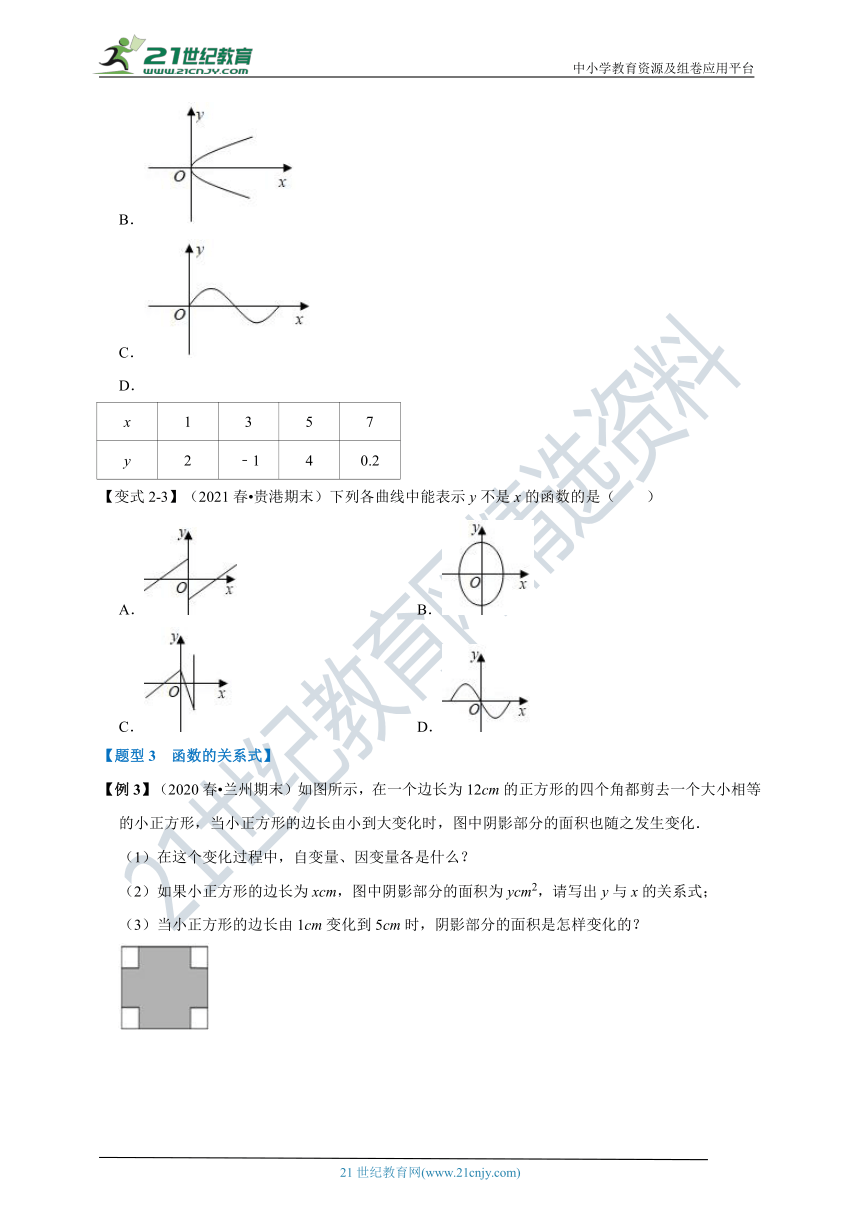
D.
x 1 3 5 7
y 2 ﹣1 4 0.2
【变式2-3】(2021春 贵港期末)下列各曲线中能表示y不是x的函数的是( )
A. B.
C. D.
【题型3 函数的关系式】
【例3】(2020春 兰州期末)如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果小正方形的边长为xcm,图中阴影部分的面积为ycm2,请写出y与x的关系式;
(3)当小正方形的边长由1cm变化到5cm时,阴影部分的面积是怎样变化的?
【变式3-1】(2021春 宁津县期末)如图,△ABC的边BC长12cm,乐乐观察到当顶点A沿着BC边上的高AD所在直线上运动时,三角形的面积发生变化.在这个变化过程中,如果三角形的高为x(cm),那么△ABC的面积y(cm2)与x(cm)的关系式是 .
【变式3-2】(2021春 垦利区期末)一辆汽车油箱内有油56升,从某地出发,每行驶1千米,耗油0.08升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化
(1)在上述变化过程中,自变量是 ;因变量是 .
(2)用表格表示汽车从出发地行驶100千米、200千米、300千米、400千米时的剩油量.
请将表格补充完整:
行驶路程x(千米) 100 200 300 400
油箱内剩油量y(升) 40 24
(3)试写出y与x的关系式 .
(4)这辆汽车行驶350千米时剩油多少升?汽车剩油8升时,行驶了多少千米?
【变式3-3】如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
链条节数(节) 2 3 4
链条长度(cm)
(2)如果x节链条的总长度是y,求y与x之间的关系式;
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?
【题型4 求函数的值】
【例4】(2020春 万州区期末)若定义f(x)=3x﹣2,如f(﹣2)=3×(﹣2)﹣2=﹣8.下列说法中:①当f(x)=1时,x=1;②对于正数x,f(x)>f(﹣x)均成立;③f(x﹣1)+f(1﹣x)=0;④当且仅当a=2时,f(a﹣x)=a﹣f(x).其中正确的是 .(填序号)
【变式4-1】(2021 碑林区校级模拟)变量x,y的一些对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 1 0 1 …
根据表格中的数据规律,当x=﹣5时,y的值是( )
A. B. C. D.
【变式4-2】(2021 达州)如图是一个运算程序示意图,若开始输入x的值为3,则输出y值为 .
【变式4-3】(2008 防城港)已知x为实数.y、z与x的关系如表格所示:根据上述表格中的数字变化规律,解答下列问题:
(1)当x为何值时,y=430?
(2)当x为何值时,y=z?
x y z
… … …
3 30×3+70 2×1×8
4 30×4+70 2×2×9
5 30×5+70 2×3×10
6 30×6+70 2×4×11
… … …
【知识点3 函数的图象】
把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做这个函数的图像,用图像表示的函数关系,更为直观和形象.
【题型5 函数的图象】
【例5】(2021 三元区校级开学)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【变式5-1】(2021春 番禺区校级期中)小新骑车去学校,骑了一会后车子出了故障,修了一会,然后继续骑车去学校.如果用横坐标表示时间t,纵坐标表示路程s,下列各图能较好地反映s与t之间函数关系的是( )
A. B.
C. D.
【变式5-2】(2021春 任城区期末)小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
【变式5-3】(2021 沙坪坝区校级开学)夏季是雷雨高发季节,为缓解暴雨带来的洪灾问题,某村在道路内侧新建了一个排水渠排水(横截面如图),某天突发暴雨,排水渠开始积水,水位上涨,暴雨停歇后,排水渠继续排水至积水全部排出,假设排水速度为5v,进水速度为7v,下列图象中,能反映以上过程排水渠中水位高度h与时间t的关系的大致图象是( )
A. B.
C. D.
【题型6 动点问题的函数图象】
【例6】(2021春 济南期中)如图1,在长方形ABCD中,点P从B点出发沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后又恢复为每秒m个单位匀速运动.在运动过程中,△ABP的面积S与运动时间t的函数关系如图2所示,则m、a、b的值分别是( )
A.m=1,a=5,b=11 B.m=1,a=4,b=12
C.m=1.5,a=5,b=12 D.m=1,a=4,b=11
【变式6-1】(2021春 怀安县期末)如图,平行四边形ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B﹣C﹣D﹣A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
A. B.
C. D.
【变式6-2】(2021春 平顶山期末)如图①,四边形ABCD是长方形,动点E从B出发,以1厘米/秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( )
A.AB=3厘米
B.长方形ABCD的周长为10厘米
C.当t=3秒时,S=3平方厘米
D.当S=1.5平方厘米时,t=6秒
【变式6-3】(2021春 南海区期末)如图,在正方形ABMF中剪去一个小正方形CDEM,动点P从点A出发,沿A→B→C→D→E→F的路线绕多边形的边匀速运动到点F时停止,则△APF的面积S随着时间t变化的图象大致是( )
A. B. C. D.
函数-重难点题型
【知识点1 函数的概念】
一般地,在某一变化过程中有两个变量x与y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
注意:要判断一个关系式是不是函数,首先看这个变化过程中是否只有两个变量,其次看每一个x的值是否对应唯一确定的y值.
【知识点2 求函数的值】
(1)当已知函数解析式时,求函数值就是求代数式的值;函数值是唯一的,而对应的自变量可以是多个.(2)函数表达式中只有两个变量,给定一个变量的值,将其代入函数表达式即可求另一个变量的值,即给自变量的值可求函数值,给函数值可求自变量的值.
【题型1 常量与变量】
【例1】如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积ycm2与MA的长度xcm之间的关系式,并指出其中的常量与变量.
【解题思路】根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系.再根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得答案.
【解答过程】解:由题意知,开始时A点与M点重合,让△ABC向右运动,两图形重合的长度为AM=x,
∵∠BAC=45°,
∴S阴影AM×hAM2,
则yx2,0<x≤10,
其中的常量为,变量为重叠部分的面积y与MA的长度x.
【变式1-1】.用同样大小的黑色棋子按如图所示的方式摆图形,按照这样的规律摆下去,则第n个图形的棋子数y= (用含n的代数式表示),其中变量是 .
【解题思路】解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.
【解答过程】解:第一个图需棋子4;
第二个图需棋子4+3=7;
第三个图需棋子4+3+3=10;
…
第n个图需棋子4+3(n﹣1)=(3n+1)枚.
其中变量是n,y.
故答案为:3n+1;y,n.
【变式1-2】按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
【解题思路】由图形可知,第一张餐桌上可以摆放6把椅子,进一步观察发现:多一张餐桌,多放4把椅子.x张餐桌共有6+4(x﹣1)=4x+2.
【解答过程】解:(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x﹣1)=4x+2个座位.
故可坐人数y=4x+2,
故答案为:有2个变量;
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
【变式1-3】在烧开水时,水温达到100℃就会沸腾,下表是某同学做“观察水的沸腾”实验时记录的数据:
(1)上表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间推移2分钟,水的温度如何变化?
(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?
(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
【解题思路】(1)在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中数据得出水的温度变化即可;
(3)根据表格中数据得出水的温度变化即可;
(4)根据表格中数据得出水的温度,进而可得出时间为9分钟时,水的温度;
(5)根据表格中数据得出水的温度变化规律即可;
(6)根据表格中数据得出答案即可.
【解答过程】解:(1)上表反映了水的温度与时间的关系,时间是自变量,水的温度是因变量;
(2)水的温度随着时间的增加而增加,到100℃时恒定;
(3)时间推移2分钟,水的温度增加14度,到10分钟时恒定;
(4)时间为8分钟,水的温度是86℃,时间为9分钟,水的温度是93℃;
(5)根据表格,时间为16分钟和18分钟时水的温度均为100℃;
(6)为了节约能源,应在10分钟后停止烧水.
【题型2 判断函数关系】
【例2】(2021春 海淀区期末)如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度h、水面的面积S及注水量V是三个变量.下列有四种说法:
①S是V的函数;②V是S的函数;③h是S的函数,④S是h的函数.
其中所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
【解题思路】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可判断函数.
【解答过程】解:因为这是球形容器,
①S是V的函数,故符合题意,
②V不是S的函数,故不符合题意,
③h不是S的函数,故不符合题意,
④S是h的函数.故符合题意.
故选:B.
【变式2-1】(2021春 开福区校级月考)下列式子中,y不是x的函数的是( )
A.y=x2 B.y=|x| C.y=2x+1 D.(x≥0)
【解题思路】利用函数的定义:给定一个自变量的值,都有唯一确定的函数值与其对应可得答案.
【解答过程】解:A、y=x2,y是x的函数,故此选项不合题意;
B、y=|x|,y是x的函数,故此选项不合题意;
C、y=2x+1,y是x的函数,故此选项不合题意;
D、y=±,y不是x的函数,故此选项符合题意;
故选:D.
【变式2-2】(2021春 邯郸期末)下列不能表示y是x的函数的是( )
A.
x 0 5 10 15
y 3 3.5 4 4.5
B.
C.
D.
x 1 3 5 7
y 2 ﹣1 4 0.2
【解题思路】根据函数的定义,一个x只能对应一个y,函数的表示方法有列表法,图像法,和解析式法,根据此定义判断即可.
【解答过程】解:A和D选项是用列表法表示的函数,一个x只对应了一个y,
∴y是x的函数,
∴A选项,D选项不合题意,
B选项从图象上看,一个x对应了两个y的值,不符合函数定义,
∴B选项符合题意,
C选项是用图象表示的函数关系,一个x只对应一个y,
∴y是x的函数,
∴C选项不合题意,
故选:B.
【变式2-3】(2021春 贵港期末)下列各曲线中能表示y不是x的函数的是( )
A. B.
C. D.
【解题思路】根据函数的定义判断.
【解答过程】解:根据函数的定义:在一个变化的过程中,如果有两个变量x与y,并且对于x的每一确定的值,y都有唯一确定的值与之对应,那么y是x的函数.
∴A、C、D选项y是x的函数,但B选项中,x的每一个确定的值,y有两个值与之对应,那么B选项y不是x的函数.
故选:B.
【题型3 函数的关系式】
【例3】(2020春 兰州期末)如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果小正方形的边长为xcm,图中阴影部分的面积为ycm2,请写出y与x的关系式;
(3)当小正方形的边长由1cm变化到5cm时,阴影部分的面积是怎样变化的?
【解题思路】(1)根据当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化,则小正方形的边长是自变量,阴影部分的面积为因变量;
(2)根据阴影部分的面积=大正方形的面积﹣4个小正方形的面积,即可解答;
(3)根据当小正方形的边长由1cm变化到5cm时,x增大,x2也随之增大,﹣4x2则随着x的增大而减小,所以y随着x的增大而减小.
【解答过程】解:(1)∵当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化,
∴小正方形的边长是自变量,阴影部分的面积为因变量;
(2)由题意可得:y=122﹣4x2=144﹣4x2.
(3)由(2)知:y=144﹣4x2,
当小正方形的边长由1cm变化到5cm时,x增大,x2也随之增大,﹣4x2则随着x的增大而减小,所以y随着x的增大而减小,
当x=1cm时,y有最大值,140(cm2).
当x=5cm时,y有最小值,y最小=144﹣4×52=44(cm2).
∴当小正方形的边长由1cm变化到5cm时,阴影部分的面积由140cm2变到44cm2
【变式3-1】(2021春 宁津县期末)如图,△ABC的边BC长12cm,乐乐观察到当顶点A沿着BC边上的高AD所在直线上运动时,三角形的面积发生变化.在这个变化过程中,如果三角形的高为x(cm),那么△ABC的面积y(cm2)与x(cm)的关系式是 .
【解题思路】利用三角形的面积公式即可得到关系式.
【解答过程】解:∵△ABC的面积BC x12 x=6x,
∴y与x的关系式为:y=6x.
故答案为:y=6x.
【变式3-2】(2021春 垦利区期末)一辆汽车油箱内有油56升,从某地出发,每行驶1千米,耗油0.08升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化
(1)在上述变化过程中,自变量是 ;因变量是 .
(2)用表格表示汽车从出发地行驶100千米、200千米、300千米、400千米时的剩油量.
请将表格补充完整:
行驶路程x(千米) 100 200 300 400
油箱内剩油量y(升) 40 24
(3)试写出y与x的关系式 .
(4)这辆汽车行驶350千米时剩油多少升?汽车剩油8升时,行驶了多少千米?
【解题思路】(1)根据已知得出即可;
(2)根据题意列出算式,即可求出答案;
(3)根据题意得出y=56﹣0.08x即可;
(4)把x=350和y=8分别代入,即可求出答案.
【解答过程】解:(1)在上述变化过程中,自变量是汽车行驶路程;因变量是邮箱内剩油量,
故答案为:汽车行驶路程,邮箱内剩油量;
(2)56﹣0.08×100=48,56﹣0.08×300=32,
(3)y与x的关系式是y=56﹣0.08x,
故答案为:y=56﹣0.08x;
(4)当x=350时,y=56﹣0.08×350=28,
所以汽车行驶350千米时剩油28升;
当y=8时,56﹣0.08x=8,
解得:x=600,
所以汽车行驶600千米时剩油8升.
【变式3-3】如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
链条节数(节) 2 3 4
链条长度(cm) 4.2 5.9 7.6
(2)如果x节链条的总长度是y,求y与x之间的关系式;
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?
【解题思路】(1)根据图形找出规律计算4节链条的长度即可;
(2)由(1)写出表示链条节数的一般式;
(3)根据(2)计算时,特别注意自行车上的链条为环形,在展直的基础上还要缩短0.8.
【解答过程】解:(1)根据图形可得出:
2节链条的长度为:2.5×2﹣0.8=4.2,
3节链条的长度为:2.5×3﹣0.8×2=5.9,
4节链条的长度为:2.5×4﹣0.8×3=7.6.
故答案为:4.2,5.9,7.6;
(2)由(1)可得x节链条长为:y=2.5x﹣0.8(x﹣1)=1.7x+0.8;
∴y与x之间的关系式为:y=1.7x+0.8;
(3)因为自行车上的链条为环形,在展直的基础上还要缩短0.8,故这辆自行车链条的总长为1.7×80=136厘米,
所以80节这样的链条总长度是136厘米.
【题型4 求函数的值】
【例4】(2020春 万州区期末)若定义f(x)=3x﹣2,如f(﹣2)=3×(﹣2)﹣2=﹣8.下列说法中:①当f(x)=1时,x=1;②对于正数x,f(x)>f(﹣x)均成立;③f(x﹣1)+f(1﹣x)=0;④当且仅当a=2时,f(a﹣x)=a﹣f(x).其中正确的是 ①②④ .(填序号)
【解题思路】根据函数的定义,计算即可判断;
【解答过程】解:∵f(x)=1,
∴3x﹣2=1,
∴x=1,故①正确,
f(x)﹣f(﹣x)=3x﹣2﹣(﹣3x﹣2)=6x,
∵x>0,
∴f(x)>f(﹣x),故②正确,
f(x﹣1)+f(1﹣x)=3(x﹣1)﹣2+3(1﹣x)﹣2=﹣4,
故③错误,
∵f(a﹣x)=3(a﹣x)﹣2=3a﹣3x﹣2,
a﹣f(x)=a﹣(3x﹣2),
∵a=2,
∴f(a﹣x)=a﹣f(x).
故答案为①②④.
【变式4-1】(2021 碑林区校级模拟)变量x,y的一些对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 1 0 1 …
根据表格中的数据规律,当x=﹣5时,y的值是( )
A. B. C. D.
【解题思路】据表格数据得到函数为y,把x=﹣5代入求得即可.
【解答过程】解:根据表格数据可知,当x=﹣1时,y=1;当x=1时,y=1;当x=﹣2时,y;当x=2时,y;
可得函数的解析式为y,
当x=﹣5时,y.
故选:B.
【变式4-2】(2021 达州)如图是一个运算程序示意图,若开始输入x的值为3,则输出y值为 2 .
【解题思路】将x=3代入y=|x|﹣1(x≤4)求解.
【解答过程】解:∵3<4,
∴把x=3代入y=|x|﹣1得y=3﹣1=2,
故答案为2.
【变式4-3】(2008 防城港)已知x为实数.y、z与x的关系如表格所示:根据上述表格中的数字变化规律,解答下列问题:
(1)当x为何值时,y=430?
(2)当x为何值时,y=z?
x y z
… … …
3 30×3+70 2×1×8
4 30×4+70 2×2×9
5 30×5+70 2×3×10
6 30×6+70 2×4×11
… … …
【解题思路】由图片中的信息可得出:当x为n(n≥3)时,y应该表示为30×n+70,z就应该表述为2×(n﹣2)(5+n);那么由此可得出(1)(2)中所求的值.
【解答过程】解:∵y=30×x+70,z=2×(x﹣2)(5+x)
(1)当x=12时,y=30×12+70=430;
(2)∵y=z,
即30×x+70=2×(x﹣2)(5+x),
解得:x=﹣3或15.
【知识点3 函数的图象】
把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做这个函数的图像,用图像表示的函数关系,更为直观和形象.
【题型5 函数的图象】
【例5】(2021 三元区校级开学)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【解题思路】根据函数的图象即可确定在BC段,所用的时间是5秒,路程是150米,则速度是30米/秒,进而即可确定其它答案.
【解答过程】解:火车的长度是150米,故①错误;
在BC段,所用的时间是5秒,路程是150米,则速度是30米/秒.故②正确;
整个火车都在隧道内的时间是:35﹣5﹣5=25(秒),故③正确;
隧道长是:35×30﹣150=1050﹣150=900(米),故④错误.
正确结论有②③共2个.
故选:B.
【变式5-1】(2021春 番禺区校级期中)小新骑车去学校,骑了一会后车子出了故障,修了一会,然后继续骑车去学校.如果用横坐标表示时间t,纵坐标表示路程s,下列各图能较好地反映s与t之间函数关系的是( )
A. B.
C. D.
【解题思路】通过小新先运动然后停止运动然后再运动对比图象求解.
【解答过程】解:小新开始骑车去学校,所以S随t增大而增大,
车子出故障后S不随时间变化而变化,
最后恢复运动,S继续随时间增大而增大,
观察图象,C满足题意.
故选:C.
【变式5-2】(2021春 任城区期末)小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
【解题思路】根据已知信息和函数图象的数据,一次解答每个选项
【解答过程】解:由图象可知,小华和小明的家离学校1200米,故A正确;
根据图象,小华乘公共汽车,从出发到到达学校共用了13﹣8=5(分钟),所以公共汽车的速度为1200÷5=240(米/分),故B正确;
小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是8+480÷240=10(分钟),即7:50相遇,故C正确;
小明从家到学校的时间为20分钟,所以小明的平均速度为1200÷20=60(米/分),故D错误.
故选:D.
【变式5-3】(2021 沙坪坝区校级开学)夏季是雷雨高发季节,为缓解暴雨带来的洪灾问题,某村在道路内侧新建了一个排水渠排水(横截面如图),某天突发暴雨,排水渠开始积水,水位上涨,暴雨停歇后,排水渠继续排水至积水全部排出,假设排水速度为5v,进水速度为7v,下列图象中,能反映以上过程排水渠中水位高度h与时间t的关系的大致图象是( )
A. B.
C. D.
【解题思路】根据题意可知在暴雨前水渠中水位高度h为0,在下暴雨过程中,由于进水速度大于排水速度,所以水渠中水位高度h逐渐增高,当暴雨停歇后,只排水,所以函数图形为先缓,后陡.据此判断即可.
【解答过程】解:在下暴雨过程中,由于进水速度大于排水速度,所以水渠中水位高度h逐渐增高,当暴雨停歇后,只排水,所以函数图形为先缓,后陡.
故选项B符合题意.
故选:B.
【题型6 动点问题的函数图象】
【例6】(2021春 济南期中)如图1,在长方形ABCD中,点P从B点出发沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后又恢复为每秒m个单位匀速运动.在运动过程中,△ABP的面积S与运动时间t的函数关系如图2所示,则m、a、b的值分别是( )
A.m=1,a=5,b=11 B.m=1,a=4,b=12
C.m=1.5,a=5,b=12 D.m=1,a=4,b=11
【解题思路】由图象可知,CD的长度,当t=6时,S△ABP=16,求出BC的长;当t=a时,S△ABP=8,则点P此时在BC的中点处,从而得出a和m的值,当t=b时,S△ABP=4,从而求得b的值;
【解答过程】解:从图象可知,当6≤t≤8时,△ABP面积不变,
即6≤t≤8时,点P从点C运动到点D,且这时速度为每秒2个单位,
∴CD=2×(8﹣6)=4,
∴AB=CD=4,
当t=6时(点P运动到点C),S△ABP=16,
∴AB BC=16,即16,
∴BC=8,
∴长方形的长为8,宽为4,
当t=a时,S△ABP=84×BP,
即点P此时在BC的中点处,
∴PCBC8=4,
∴2(6﹣a)=4,
∴a=4,
∵BP=PC=4,
∴m=BP÷a=4÷4=1,
当t=b时,S△ABPAB AP=4,
∴4×AP=4,AP=2,
∴b=13﹣2=11,
∴m=1,a=4,b=11,
故选:D.
【变式6-1】(2021春 怀安县期末)如图,平行四边形ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B﹣C﹣D﹣A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
A. B.
C. D.
【解题思路】当点E在BC上运动时,三角形的面积不断增大,当点E在DC上运动时,三角形的面积不变,当点E在AD上运动时三角形的面积不等减小,然后计算出三角形的最大面积即可得出答案.
【解答过程】解:当点E在BC上运动时,三角形的面积不断增大,最大面积34=3;
当点E在DC上运动时,三角形的面积为定值3.
当点E在AD上运动时三角形的面不断减小,当点E与点A重合时,面积为0.
故选:D.
【变式6-2】(2021春 平顶山期末)如图①,四边形ABCD是长方形,动点E从B出发,以1厘米/秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( )
A.AB=3厘米
B.长方形ABCD的周长为10厘米
C.当t=3秒时,S=3平方厘米
D.当S=1.5平方厘米时,t=6秒
【解题思路】通过图②发现:t=2、5、7时,△ABE的面积为S的变化趋势发生变化得到长方形的长和宽,从而判断出A、B选项正确;t=3秒时点E在DA上运动根据三角形面积公式可判断C正确;S=1.5平方厘米时,点E可能在BC上,也可能在DA上,求出此时的t值即可.
【解答过程】解:∵0≤t≤2时,△ABE的面积S越来越大,
∴0≤t≤2时,动点E在BC上运动,
∴BC=2×1=2(厘米).
∵2≤t≤5时,△ABE的面积S不变,
∴0≤t≤2时,动点E在CD上运动,
∴CD=AB=(5﹣2)×1=3(厘米).
∴A选项正确,不符合题意.
长方形ABCD的周长=(3+2)×2=10(厘米),
∴B选项正确,不符合题意.
∵2<3<5,
∴当t=3秒时,动点E在CD上运动,S=3×2÷2=3(平方厘米),
∴B选项正确,不符合题意.
∵S=1.5<3,
∴S=1.5平方厘米时,点E在BC或DA上,
当点E在DA上时,
t×31.5,
解得:t=1,
当点E在DA上时,
(t﹣3﹣2)1.5,
解得:t=6,
∴S=1.5平方厘米时,t=6或1.
∴D选项错误,符合题意.
故选:D.
【变式6-3】(2021春 南海区期末)如图,在正方形ABMF中剪去一个小正方形CDEM,动点P从点A出发,沿A→B→C→D→E→F的路线绕多边形的边匀速运动到点F时停止,则△APF的面积S随着时间t变化的图象大致是( )
A. B. C. D.
【解题思路】根据点P在AB、BC、CD、DE、EF上时,△APF的面积S与时间t的变化趋势确定函数图象.
【解答过程】解:当点P在AB上时,△APF的底AF不变,高增大,所以△APF的面积S随着时间t的增大而增大;
当点P在BC上时,△APF的底AF不变,高不变,所以△APF的面积S不变;
当点P在CD上时,△APF的底AF不变,高减小,所以△APF的面积S随着时间t的增大而减小;
当点P在DE上时,△APF的底AF不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△APF的底AF不变,高减小,所以△ABP的面积S随着时间t的增大而减小.
故选:C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
函数6大题型
【知识点1 函数的概念】
一般地,在某一变化过程中有两个变量x与y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
注意:要判断一个关系式是不是函数,首先看这个变化过程中是否只有两个变量,其次看每一个x的值是否对应唯一确定的y值.
【知识点2 求函数的值】
(1)当已知函数解析式时,求函数值就是求代数式的值;函数值是唯一的,而对应的自变量可以是多个.(2)函数表达式中只有两个变量,给定一个变量的值,将其代入函数表达式即可求另一个变量的值,即给自变量的值可求函数值,给函数值可求自变量的值.
【题型1 常量与变量】
【例1】如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积ycm2与MA的长度xcm之间的关系式,并指出其中的常量与变量.
【变式1-1】.用同样大小的黑色棋子按如图所示的方式摆图形,按照这样的规律摆下去,则第n个图形的棋子数y= (用含n的代数式表示),其中变量是 .
【变式1-2】按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
【变式1-3】在烧开水时,水温达到100℃就会沸腾,下表是某同学做“观察水的沸腾”实验时记录的数据:
(1)上表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间推移2分钟,水的温度如何变化?
(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?
(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
【题型2 判断函数关系】
【例2】(2021春 海淀区期末)如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度h、水面的面积S及注水量V是三个变量.下列有四种说法:
①S是V的函数;②V是S的函数;③h是S的函数,④S是h的函数.
其中所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
【变式2-1】(2021春 开福区校级月考)下列式子中,y不是x的函数的是( )
A.y=x2 B.y=|x| C.y=2x+1 D.(x≥0)
【变式2-2】(2021春 邯郸期末)下列不能表示y是x的函数的是( )
A.
x 0 5 10 15
y 3 3.5 4 4.5
B.
C.
D.
x 1 3 5 7
y 2 ﹣1 4 0.2
【变式2-3】(2021春 贵港期末)下列各曲线中能表示y不是x的函数的是( )
A. B.
C. D.
【题型3 函数的关系式】
【例3】(2020春 兰州期末)如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果小正方形的边长为xcm,图中阴影部分的面积为ycm2,请写出y与x的关系式;
(3)当小正方形的边长由1cm变化到5cm时,阴影部分的面积是怎样变化的?
【变式3-1】(2021春 宁津县期末)如图,△ABC的边BC长12cm,乐乐观察到当顶点A沿着BC边上的高AD所在直线上运动时,三角形的面积发生变化.在这个变化过程中,如果三角形的高为x(cm),那么△ABC的面积y(cm2)与x(cm)的关系式是 .
【变式3-2】(2021春 垦利区期末)一辆汽车油箱内有油56升,从某地出发,每行驶1千米,耗油0.08升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化
(1)在上述变化过程中,自变量是 ;因变量是 .
(2)用表格表示汽车从出发地行驶100千米、200千米、300千米、400千米时的剩油量.
请将表格补充完整:
行驶路程x(千米) 100 200 300 400
油箱内剩油量y(升) 40 24
(3)试写出y与x的关系式 .
(4)这辆汽车行驶350千米时剩油多少升?汽车剩油8升时,行驶了多少千米?
【变式3-3】如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
链条节数(节) 2 3 4
链条长度(cm)
(2)如果x节链条的总长度是y,求y与x之间的关系式;
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?
【题型4 求函数的值】
【例4】(2020春 万州区期末)若定义f(x)=3x﹣2,如f(﹣2)=3×(﹣2)﹣2=﹣8.下列说法中:①当f(x)=1时,x=1;②对于正数x,f(x)>f(﹣x)均成立;③f(x﹣1)+f(1﹣x)=0;④当且仅当a=2时,f(a﹣x)=a﹣f(x).其中正确的是 .(填序号)
【变式4-1】(2021 碑林区校级模拟)变量x,y的一些对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 1 0 1 …
根据表格中的数据规律,当x=﹣5时,y的值是( )
A. B. C. D.
【变式4-2】(2021 达州)如图是一个运算程序示意图,若开始输入x的值为3,则输出y值为 .
【变式4-3】(2008 防城港)已知x为实数.y、z与x的关系如表格所示:根据上述表格中的数字变化规律,解答下列问题:
(1)当x为何值时,y=430?
(2)当x为何值时,y=z?
x y z
… … …
3 30×3+70 2×1×8
4 30×4+70 2×2×9
5 30×5+70 2×3×10
6 30×6+70 2×4×11
… … …
【知识点3 函数的图象】
把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做这个函数的图像,用图像表示的函数关系,更为直观和形象.
【题型5 函数的图象】
【例5】(2021 三元区校级开学)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【变式5-1】(2021春 番禺区校级期中)小新骑车去学校,骑了一会后车子出了故障,修了一会,然后继续骑车去学校.如果用横坐标表示时间t,纵坐标表示路程s,下列各图能较好地反映s与t之间函数关系的是( )
A. B.
C. D.
【变式5-2】(2021春 任城区期末)小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
【变式5-3】(2021 沙坪坝区校级开学)夏季是雷雨高发季节,为缓解暴雨带来的洪灾问题,某村在道路内侧新建了一个排水渠排水(横截面如图),某天突发暴雨,排水渠开始积水,水位上涨,暴雨停歇后,排水渠继续排水至积水全部排出,假设排水速度为5v,进水速度为7v,下列图象中,能反映以上过程排水渠中水位高度h与时间t的关系的大致图象是( )
A. B.
C. D.
【题型6 动点问题的函数图象】
【例6】(2021春 济南期中)如图1,在长方形ABCD中,点P从B点出发沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后又恢复为每秒m个单位匀速运动.在运动过程中,△ABP的面积S与运动时间t的函数关系如图2所示,则m、a、b的值分别是( )
A.m=1,a=5,b=11 B.m=1,a=4,b=12
C.m=1.5,a=5,b=12 D.m=1,a=4,b=11
【变式6-1】(2021春 怀安县期末)如图,平行四边形ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B﹣C﹣D﹣A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
A. B.
C. D.
【变式6-2】(2021春 平顶山期末)如图①,四边形ABCD是长方形,动点E从B出发,以1厘米/秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( )
A.AB=3厘米
B.长方形ABCD的周长为10厘米
C.当t=3秒时,S=3平方厘米
D.当S=1.5平方厘米时,t=6秒
【变式6-3】(2021春 南海区期末)如图,在正方形ABMF中剪去一个小正方形CDEM,动点P从点A出发,沿A→B→C→D→E→F的路线绕多边形的边匀速运动到点F时停止,则△APF的面积S随着时间t变化的图象大致是( )
A. B. C. D.
函数-重难点题型
【知识点1 函数的概念】
一般地,在某一变化过程中有两个变量x与y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
注意:要判断一个关系式是不是函数,首先看这个变化过程中是否只有两个变量,其次看每一个x的值是否对应唯一确定的y值.
【知识点2 求函数的值】
(1)当已知函数解析式时,求函数值就是求代数式的值;函数值是唯一的,而对应的自变量可以是多个.(2)函数表达式中只有两个变量,给定一个变量的值,将其代入函数表达式即可求另一个变量的值,即给自变量的值可求函数值,给函数值可求自变量的值.
【题型1 常量与变量】
【例1】如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积ycm2与MA的长度xcm之间的关系式,并指出其中的常量与变量.
【解题思路】根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系.再根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得答案.
【解答过程】解:由题意知,开始时A点与M点重合,让△ABC向右运动,两图形重合的长度为AM=x,
∵∠BAC=45°,
∴S阴影AM×hAM2,
则yx2,0<x≤10,
其中的常量为,变量为重叠部分的面积y与MA的长度x.
【变式1-1】.用同样大小的黑色棋子按如图所示的方式摆图形,按照这样的规律摆下去,则第n个图形的棋子数y= (用含n的代数式表示),其中变量是 .
【解题思路】解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.
【解答过程】解:第一个图需棋子4;
第二个图需棋子4+3=7;
第三个图需棋子4+3+3=10;
…
第n个图需棋子4+3(n﹣1)=(3n+1)枚.
其中变量是n,y.
故答案为:3n+1;y,n.
【变式1-2】按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
(1)题中有几个变量?
(2)你能写出两个变量之间的关系吗?
【解题思路】由图形可知,第一张餐桌上可以摆放6把椅子,进一步观察发现:多一张餐桌,多放4把椅子.x张餐桌共有6+4(x﹣1)=4x+2.
【解答过程】解:(1)观察图形:x=1时,y=6,x=2时,y=10;x=3时,y=14;…
可见每增加一张桌子,便增加4个座位,
因此x张餐桌共有6+4(x﹣1)=4x+2个座位.
故可坐人数y=4x+2,
故答案为:有2个变量;
(2)能,由(1)分析可得:函数关系式可以为y=4x+2.
【变式1-3】在烧开水时,水温达到100℃就会沸腾,下表是某同学做“观察水的沸腾”实验时记录的数据:
(1)上表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间推移2分钟,水的温度如何变化?
(4)时间为8分钟,水的温度为多少?你能得出时间为9分钟时,水的温度吗?
(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
【解题思路】(1)在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中数据得出水的温度变化即可;
(3)根据表格中数据得出水的温度变化即可;
(4)根据表格中数据得出水的温度,进而可得出时间为9分钟时,水的温度;
(5)根据表格中数据得出水的温度变化规律即可;
(6)根据表格中数据得出答案即可.
【解答过程】解:(1)上表反映了水的温度与时间的关系,时间是自变量,水的温度是因变量;
(2)水的温度随着时间的增加而增加,到100℃时恒定;
(3)时间推移2分钟,水的温度增加14度,到10分钟时恒定;
(4)时间为8分钟,水的温度是86℃,时间为9分钟,水的温度是93℃;
(5)根据表格,时间为16分钟和18分钟时水的温度均为100℃;
(6)为了节约能源,应在10分钟后停止烧水.
【题型2 判断函数关系】
【例2】(2021春 海淀区期末)如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度h、水面的面积S及注水量V是三个变量.下列有四种说法:
①S是V的函数;②V是S的函数;③h是S的函数,④S是h的函数.
其中所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
【解题思路】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可判断函数.
【解答过程】解:因为这是球形容器,
①S是V的函数,故符合题意,
②V不是S的函数,故不符合题意,
③h不是S的函数,故不符合题意,
④S是h的函数.故符合题意.
故选:B.
【变式2-1】(2021春 开福区校级月考)下列式子中,y不是x的函数的是( )
A.y=x2 B.y=|x| C.y=2x+1 D.(x≥0)
【解题思路】利用函数的定义:给定一个自变量的值,都有唯一确定的函数值与其对应可得答案.
【解答过程】解:A、y=x2,y是x的函数,故此选项不合题意;
B、y=|x|,y是x的函数,故此选项不合题意;
C、y=2x+1,y是x的函数,故此选项不合题意;
D、y=±,y不是x的函数,故此选项符合题意;
故选:D.
【变式2-2】(2021春 邯郸期末)下列不能表示y是x的函数的是( )
A.
x 0 5 10 15
y 3 3.5 4 4.5
B.
C.
D.
x 1 3 5 7
y 2 ﹣1 4 0.2
【解题思路】根据函数的定义,一个x只能对应一个y,函数的表示方法有列表法,图像法,和解析式法,根据此定义判断即可.
【解答过程】解:A和D选项是用列表法表示的函数,一个x只对应了一个y,
∴y是x的函数,
∴A选项,D选项不合题意,
B选项从图象上看,一个x对应了两个y的值,不符合函数定义,
∴B选项符合题意,
C选项是用图象表示的函数关系,一个x只对应一个y,
∴y是x的函数,
∴C选项不合题意,
故选:B.
【变式2-3】(2021春 贵港期末)下列各曲线中能表示y不是x的函数的是( )
A. B.
C. D.
【解题思路】根据函数的定义判断.
【解答过程】解:根据函数的定义:在一个变化的过程中,如果有两个变量x与y,并且对于x的每一确定的值,y都有唯一确定的值与之对应,那么y是x的函数.
∴A、C、D选项y是x的函数,但B选项中,x的每一个确定的值,y有两个值与之对应,那么B选项y不是x的函数.
故选:B.
【题型3 函数的关系式】
【例3】(2020春 兰州期末)如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果小正方形的边长为xcm,图中阴影部分的面积为ycm2,请写出y与x的关系式;
(3)当小正方形的边长由1cm变化到5cm时,阴影部分的面积是怎样变化的?
【解题思路】(1)根据当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化,则小正方形的边长是自变量,阴影部分的面积为因变量;
(2)根据阴影部分的面积=大正方形的面积﹣4个小正方形的面积,即可解答;
(3)根据当小正方形的边长由1cm变化到5cm时,x增大,x2也随之增大,﹣4x2则随着x的增大而减小,所以y随着x的增大而减小.
【解答过程】解:(1)∵当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化,
∴小正方形的边长是自变量,阴影部分的面积为因变量;
(2)由题意可得:y=122﹣4x2=144﹣4x2.
(3)由(2)知:y=144﹣4x2,
当小正方形的边长由1cm变化到5cm时,x增大,x2也随之增大,﹣4x2则随着x的增大而减小,所以y随着x的增大而减小,
当x=1cm时,y有最大值,140(cm2).
当x=5cm时,y有最小值,y最小=144﹣4×52=44(cm2).
∴当小正方形的边长由1cm变化到5cm时,阴影部分的面积由140cm2变到44cm2
【变式3-1】(2021春 宁津县期末)如图,△ABC的边BC长12cm,乐乐观察到当顶点A沿着BC边上的高AD所在直线上运动时,三角形的面积发生变化.在这个变化过程中,如果三角形的高为x(cm),那么△ABC的面积y(cm2)与x(cm)的关系式是 .
【解题思路】利用三角形的面积公式即可得到关系式.
【解答过程】解:∵△ABC的面积BC x12 x=6x,
∴y与x的关系式为:y=6x.
故答案为:y=6x.
【变式3-2】(2021春 垦利区期末)一辆汽车油箱内有油56升,从某地出发,每行驶1千米,耗油0.08升,如果设油箱内剩油量为y(升),行驶路程为x(千米),则y随x的变化而变化
(1)在上述变化过程中,自变量是 ;因变量是 .
(2)用表格表示汽车从出发地行驶100千米、200千米、300千米、400千米时的剩油量.
请将表格补充完整:
行驶路程x(千米) 100 200 300 400
油箱内剩油量y(升) 40 24
(3)试写出y与x的关系式 .
(4)这辆汽车行驶350千米时剩油多少升?汽车剩油8升时,行驶了多少千米?
【解题思路】(1)根据已知得出即可;
(2)根据题意列出算式,即可求出答案;
(3)根据题意得出y=56﹣0.08x即可;
(4)把x=350和y=8分别代入,即可求出答案.
【解答过程】解:(1)在上述变化过程中,自变量是汽车行驶路程;因变量是邮箱内剩油量,
故答案为:汽车行驶路程,邮箱内剩油量;
(2)56﹣0.08×100=48,56﹣0.08×300=32,
(3)y与x的关系式是y=56﹣0.08x,
故答案为:y=56﹣0.08x;
(4)当x=350时,y=56﹣0.08×350=28,
所以汽车行驶350千米时剩油28升;
当y=8时,56﹣0.08x=8,
解得:x=600,
所以汽车行驶600千米时剩油8升.
【变式3-3】如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
链条节数(节) 2 3 4
链条长度(cm) 4.2 5.9 7.6
(2)如果x节链条的总长度是y,求y与x之间的关系式;
(3)如果一辆某种型号自行车的链条(安装前)由80节这样的链条组成,那么这根链条完成链接(安装到自行车上)后,总长度是多少cm?
【解题思路】(1)根据图形找出规律计算4节链条的长度即可;
(2)由(1)写出表示链条节数的一般式;
(3)根据(2)计算时,特别注意自行车上的链条为环形,在展直的基础上还要缩短0.8.
【解答过程】解:(1)根据图形可得出:
2节链条的长度为:2.5×2﹣0.8=4.2,
3节链条的长度为:2.5×3﹣0.8×2=5.9,
4节链条的长度为:2.5×4﹣0.8×3=7.6.
故答案为:4.2,5.9,7.6;
(2)由(1)可得x节链条长为:y=2.5x﹣0.8(x﹣1)=1.7x+0.8;
∴y与x之间的关系式为:y=1.7x+0.8;
(3)因为自行车上的链条为环形,在展直的基础上还要缩短0.8,故这辆自行车链条的总长为1.7×80=136厘米,
所以80节这样的链条总长度是136厘米.
【题型4 求函数的值】
【例4】(2020春 万州区期末)若定义f(x)=3x﹣2,如f(﹣2)=3×(﹣2)﹣2=﹣8.下列说法中:①当f(x)=1时,x=1;②对于正数x,f(x)>f(﹣x)均成立;③f(x﹣1)+f(1﹣x)=0;④当且仅当a=2时,f(a﹣x)=a﹣f(x).其中正确的是 ①②④ .(填序号)
【解题思路】根据函数的定义,计算即可判断;
【解答过程】解:∵f(x)=1,
∴3x﹣2=1,
∴x=1,故①正确,
f(x)﹣f(﹣x)=3x﹣2﹣(﹣3x﹣2)=6x,
∵x>0,
∴f(x)>f(﹣x),故②正确,
f(x﹣1)+f(1﹣x)=3(x﹣1)﹣2+3(1﹣x)﹣2=﹣4,
故③错误,
∵f(a﹣x)=3(a﹣x)﹣2=3a﹣3x﹣2,
a﹣f(x)=a﹣(3x﹣2),
∵a=2,
∴f(a﹣x)=a﹣f(x).
故答案为①②④.
【变式4-1】(2021 碑林区校级模拟)变量x,y的一些对应值如下表:
x … ﹣2 ﹣1 0 1 2 3 …
y … 1 0 1 …
根据表格中的数据规律,当x=﹣5时,y的值是( )
A. B. C. D.
【解题思路】据表格数据得到函数为y,把x=﹣5代入求得即可.
【解答过程】解:根据表格数据可知,当x=﹣1时,y=1;当x=1时,y=1;当x=﹣2时,y;当x=2时,y;
可得函数的解析式为y,
当x=﹣5时,y.
故选:B.
【变式4-2】(2021 达州)如图是一个运算程序示意图,若开始输入x的值为3,则输出y值为 2 .
【解题思路】将x=3代入y=|x|﹣1(x≤4)求解.
【解答过程】解:∵3<4,
∴把x=3代入y=|x|﹣1得y=3﹣1=2,
故答案为2.
【变式4-3】(2008 防城港)已知x为实数.y、z与x的关系如表格所示:根据上述表格中的数字变化规律,解答下列问题:
(1)当x为何值时,y=430?
(2)当x为何值时,y=z?
x y z
… … …
3 30×3+70 2×1×8
4 30×4+70 2×2×9
5 30×5+70 2×3×10
6 30×6+70 2×4×11
… … …
【解题思路】由图片中的信息可得出:当x为n(n≥3)时,y应该表示为30×n+70,z就应该表述为2×(n﹣2)(5+n);那么由此可得出(1)(2)中所求的值.
【解答过程】解:∵y=30×x+70,z=2×(x﹣2)(5+x)
(1)当x=12时,y=30×12+70=430;
(2)∵y=z,
即30×x+70=2×(x﹣2)(5+x),
解得:x=﹣3或15.
【知识点3 函数的图象】
把一个函数的自变量x的值与对应的函数y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做这个函数的图像,用图像表示的函数关系,更为直观和形象.
【题型5 函数的图象】
【例5】(2021 三元区校级开学)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【解题思路】根据函数的图象即可确定在BC段,所用的时间是5秒,路程是150米,则速度是30米/秒,进而即可确定其它答案.
【解答过程】解:火车的长度是150米,故①错误;
在BC段,所用的时间是5秒,路程是150米,则速度是30米/秒.故②正确;
整个火车都在隧道内的时间是:35﹣5﹣5=25(秒),故③正确;
隧道长是:35×30﹣150=1050﹣150=900(米),故④错误.
正确结论有②③共2个.
故选:B.
【变式5-1】(2021春 番禺区校级期中)小新骑车去学校,骑了一会后车子出了故障,修了一会,然后继续骑车去学校.如果用横坐标表示时间t,纵坐标表示路程s,下列各图能较好地反映s与t之间函数关系的是( )
A. B.
C. D.
【解题思路】通过小新先运动然后停止运动然后再运动对比图象求解.
【解答过程】解:小新开始骑车去学校,所以S随t增大而增大,
车子出故障后S不随时间变化而变化,
最后恢复运动,S继续随时间增大而增大,
观察图象,C满足题意.
故选:C.
【变式5-2】(2021春 任城区期末)小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程S(米)和所用时间t(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米
B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇
D.小明从家到学校的平均速度为80米/分
【解题思路】根据已知信息和函数图象的数据,一次解答每个选项
【解答过程】解:由图象可知,小华和小明的家离学校1200米,故A正确;
根据图象,小华乘公共汽车,从出发到到达学校共用了13﹣8=5(分钟),所以公共汽车的速度为1200÷5=240(米/分),故B正确;
小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是8+480÷240=10(分钟),即7:50相遇,故C正确;
小明从家到学校的时间为20分钟,所以小明的平均速度为1200÷20=60(米/分),故D错误.
故选:D.
【变式5-3】(2021 沙坪坝区校级开学)夏季是雷雨高发季节,为缓解暴雨带来的洪灾问题,某村在道路内侧新建了一个排水渠排水(横截面如图),某天突发暴雨,排水渠开始积水,水位上涨,暴雨停歇后,排水渠继续排水至积水全部排出,假设排水速度为5v,进水速度为7v,下列图象中,能反映以上过程排水渠中水位高度h与时间t的关系的大致图象是( )
A. B.
C. D.
【解题思路】根据题意可知在暴雨前水渠中水位高度h为0,在下暴雨过程中,由于进水速度大于排水速度,所以水渠中水位高度h逐渐增高,当暴雨停歇后,只排水,所以函数图形为先缓,后陡.据此判断即可.
【解答过程】解:在下暴雨过程中,由于进水速度大于排水速度,所以水渠中水位高度h逐渐增高,当暴雨停歇后,只排水,所以函数图形为先缓,后陡.
故选项B符合题意.
故选:B.
【题型6 动点问题的函数图象】
【例6】(2021春 济南期中)如图1,在长方形ABCD中,点P从B点出发沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后又恢复为每秒m个单位匀速运动.在运动过程中,△ABP的面积S与运动时间t的函数关系如图2所示,则m、a、b的值分别是( )
A.m=1,a=5,b=11 B.m=1,a=4,b=12
C.m=1.5,a=5,b=12 D.m=1,a=4,b=11
【解题思路】由图象可知,CD的长度,当t=6时,S△ABP=16,求出BC的长;当t=a时,S△ABP=8,则点P此时在BC的中点处,从而得出a和m的值,当t=b时,S△ABP=4,从而求得b的值;
【解答过程】解:从图象可知,当6≤t≤8时,△ABP面积不变,
即6≤t≤8时,点P从点C运动到点D,且这时速度为每秒2个单位,
∴CD=2×(8﹣6)=4,
∴AB=CD=4,
当t=6时(点P运动到点C),S△ABP=16,
∴AB BC=16,即16,
∴BC=8,
∴长方形的长为8,宽为4,
当t=a时,S△ABP=84×BP,
即点P此时在BC的中点处,
∴PCBC8=4,
∴2(6﹣a)=4,
∴a=4,
∵BP=PC=4,
∴m=BP÷a=4÷4=1,
当t=b时,S△ABPAB AP=4,
∴4×AP=4,AP=2,
∴b=13﹣2=11,
∴m=1,a=4,b=11,
故选:D.
【变式6-1】(2021春 怀安县期末)如图,平行四边形ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B﹣C﹣D﹣A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
A. B.
C. D.
【解题思路】当点E在BC上运动时,三角形的面积不断增大,当点E在DC上运动时,三角形的面积不变,当点E在AD上运动时三角形的面积不等减小,然后计算出三角形的最大面积即可得出答案.
【解答过程】解:当点E在BC上运动时,三角形的面积不断增大,最大面积34=3;
当点E在DC上运动时,三角形的面积为定值3.
当点E在AD上运动时三角形的面不断减小,当点E与点A重合时,面积为0.
故选:D.
【变式6-2】(2021春 平顶山期末)如图①,四边形ABCD是长方形,动点E从B出发,以1厘米/秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( )
A.AB=3厘米
B.长方形ABCD的周长为10厘米
C.当t=3秒时,S=3平方厘米
D.当S=1.5平方厘米时,t=6秒
【解题思路】通过图②发现:t=2、5、7时,△ABE的面积为S的变化趋势发生变化得到长方形的长和宽,从而判断出A、B选项正确;t=3秒时点E在DA上运动根据三角形面积公式可判断C正确;S=1.5平方厘米时,点E可能在BC上,也可能在DA上,求出此时的t值即可.
【解答过程】解:∵0≤t≤2时,△ABE的面积S越来越大,
∴0≤t≤2时,动点E在BC上运动,
∴BC=2×1=2(厘米).
∵2≤t≤5时,△ABE的面积S不变,
∴0≤t≤2时,动点E在CD上运动,
∴CD=AB=(5﹣2)×1=3(厘米).
∴A选项正确,不符合题意.
长方形ABCD的周长=(3+2)×2=10(厘米),
∴B选项正确,不符合题意.
∵2<3<5,
∴当t=3秒时,动点E在CD上运动,S=3×2÷2=3(平方厘米),
∴B选项正确,不符合题意.
∵S=1.5<3,
∴S=1.5平方厘米时,点E在BC或DA上,
当点E在DA上时,
t×31.5,
解得:t=1,
当点E在DA上时,
(t﹣3﹣2)1.5,
解得:t=6,
∴S=1.5平方厘米时,t=6或1.
∴D选项错误,符合题意.
故选:D.
【变式6-3】(2021春 南海区期末)如图,在正方形ABMF中剪去一个小正方形CDEM,动点P从点A出发,沿A→B→C→D→E→F的路线绕多边形的边匀速运动到点F时停止,则△APF的面积S随着时间t变化的图象大致是( )
A. B. C. D.
【解题思路】根据点P在AB、BC、CD、DE、EF上时,△APF的面积S与时间t的变化趋势确定函数图象.
【解答过程】解:当点P在AB上时,△APF的底AF不变,高增大,所以△APF的面积S随着时间t的增大而增大;
当点P在BC上时,△APF的底AF不变,高不变,所以△APF的面积S不变;
当点P在CD上时,△APF的底AF不变,高减小,所以△APF的面积S随着时间t的增大而减小;
当点P在DE上时,△APF的底AF不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△APF的底AF不变,高减小,所以△ABP的面积S随着时间t的增大而减小.
故选:C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
