第五章一次函数专题5.3 一次函数的图象与性质-重难点题型(含解析)
文档属性
| 名称 | 第五章一次函数专题5.3 一次函数的图象与性质-重难点题型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 16:25:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
一次函数的图象与性质6大题型
【知识点1 一次函数与正比例函数的图象】
1、一次函数的图像: 所有一次函数的图像都是一条直线
2、一次函数、正比例函数图像的主要特征:
k的符号 b的符号 函数图像 图像特征
k>0 b>0 图像经过一、二、三象限,y随x的增大而增大。
b<0 图像经过一、三、四象限,y随x的增大而增大。
k<0 b>0 图像经过一、二、四象限,y随x的增大而减小
b<0 图像经过二、三、四象限,y随x的增大而减小。
注:当b=0时,一次函数变为正比例函数,正比例函数是一次函数的特例。
【题型1 一次函数的图象】
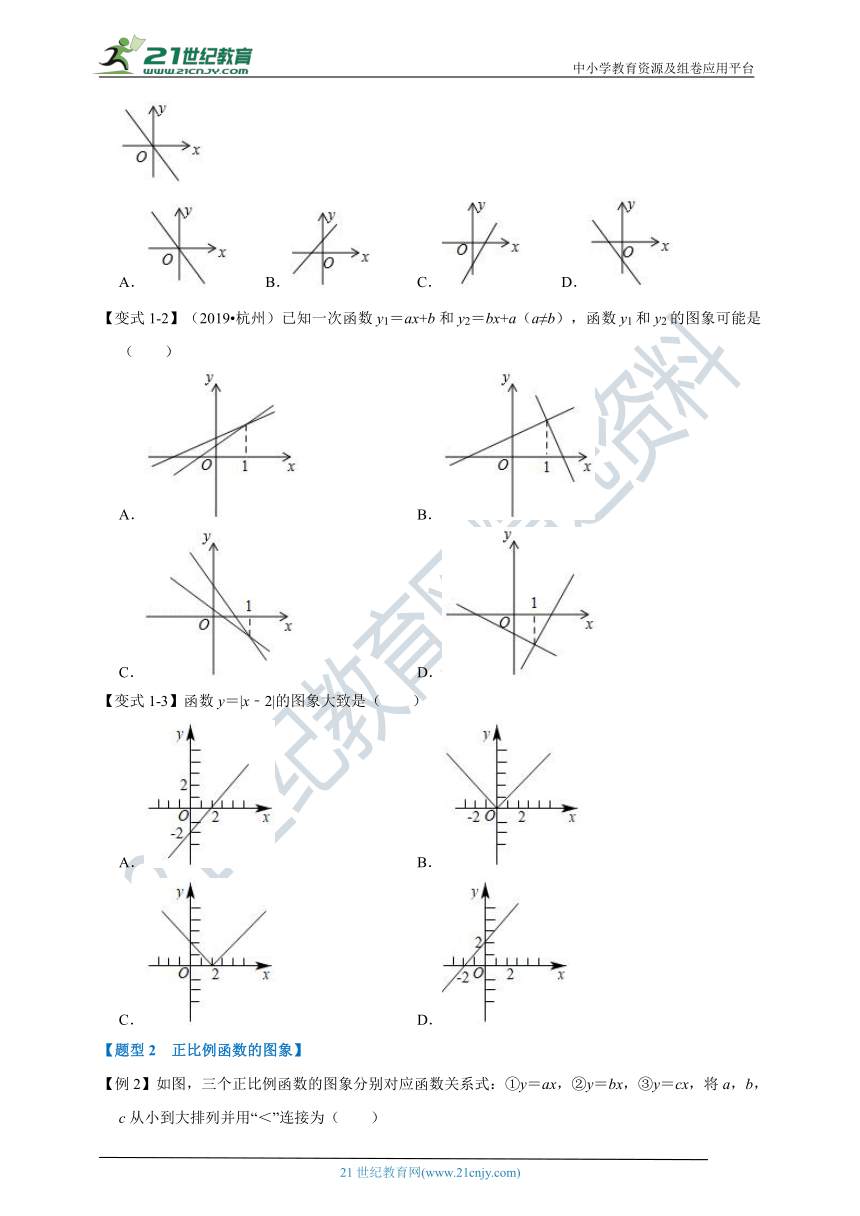
【例1】(2021 萧山区模拟)若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=﹣cx﹣a的图象可能是( )
A. B.
C. D.
【变式1-1】函数y=ax+b﹣2的图象如图所示,则函数y=﹣ax﹣b的大致图象是( )
A. B. C. D.
【变式1-2】(2019 杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )
A. B.
C. D.
【变式1-3】函数y=|x﹣2|的图象大致是( )
A. B.
C. D.
【题型2 正比例函数的图象】
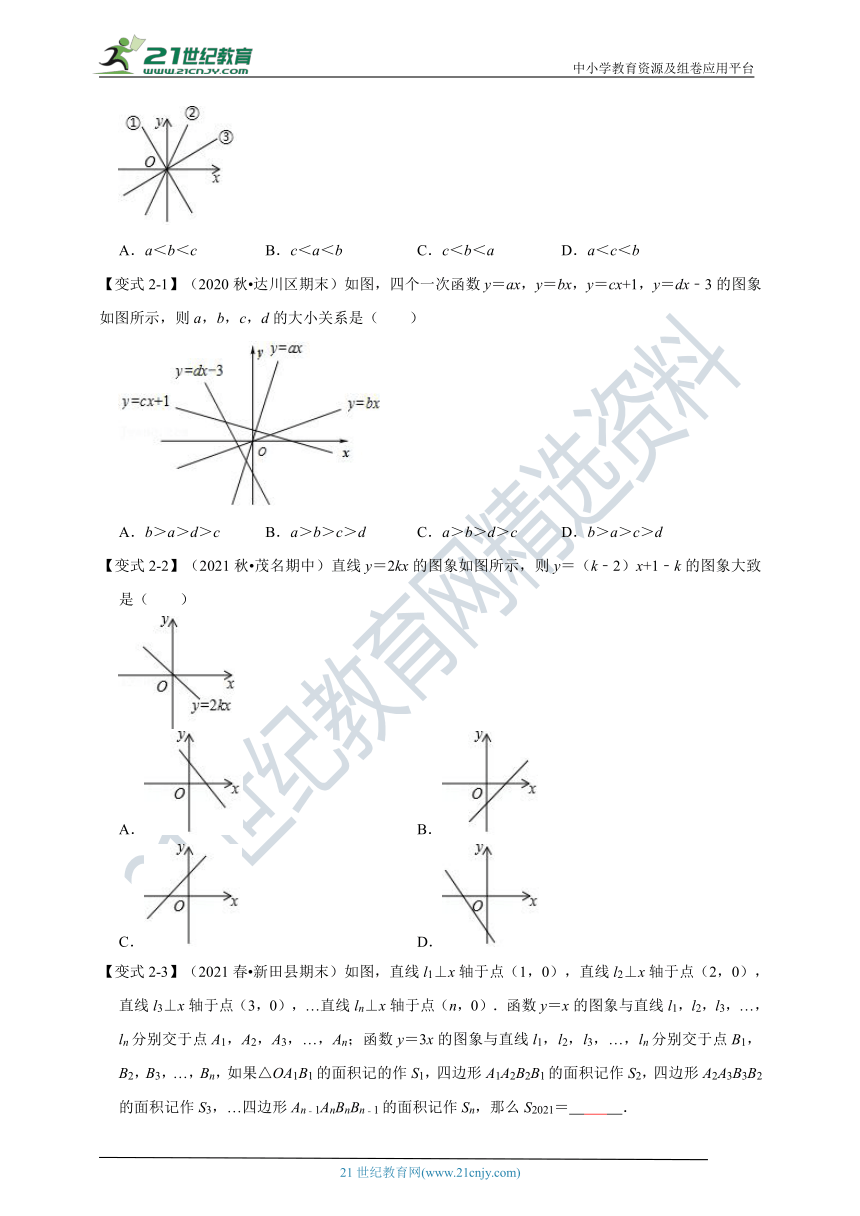
【例2】如图,三个正比例函数的图象分别对应函数关系式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为( )
A.a<b<c B.c<a<b C.c<b<a D.a<c<b
【变式2-1】(2020秋 达川区期末)如图,四个一次函数y=ax,y=bx,y=cx+1,y=dx﹣3的图象如图所示,则a,b,c,d的大小关系是( )
A.b>a>d>c B.a>b>c>d C.a>b>d>c D.b>a>c>d
【变式2-2】(2021秋 茂名期中)直线y=2kx的图象如图所示,则y=(k﹣2)x+1﹣k的图象大致是( )
A. B.
C. D.
【变式2-3】(2021春 新田县期末)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=3x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn,如果△OA1B1的面积记的作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2021= .
.
【知识点2 一次函数与正比例函数的性质】
1.一般地,正比例函数有下列性质:
(1)当k>0时,图像经过第一、三象限,y随x的增大而增大;
(2)当k<0时,图像经过第二、四象限,y随x的增大而减小。
2.一般地,一次函数有下列性质:
(1)当k>0时,y随x的增大而增大
(2)当k<0时,y随x的增大而减小
【题型3 一次函数的性质】
【例3】(2021 萧山区一模)已知y﹣3与x+5成正比例,且当x=﹣2时,y<0,则y关于x的函数图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
【变式3-1】(2021 黄州区校级自主招生)已知过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,设s=a﹣2b,则s的取值范围是( )
A. B.﹣3<s≤3 C.﹣6<s D.
【变式3-2】(2021春 忠县期末)已知一次函数y=(5﹣a)x+a+1的图象不经过第四象限,且关于x的分式方程有整数解,则满足条件的所有整数a的和为( )
A.6 B.7 C.8 D.9
【变式3-3】(2021 渝中区模拟)若关于x的一元一次不等式组恰有3个整数解,且一次函数y=(a﹣2)x+a+1不经过第三象限,则所有满足条件的整数a的值之和是( )
A.﹣2 B.﹣1 C.0 D.1
【题型4 一次函数图象与系数的关系】
【例4】(2021春 鄢陵县期末)已知A(x1,y1)、B(x2,y2)是一次函数y=(2﹣m)x+3图象上两点,且(x1﹣x2)(y1﹣y2)<0,则m的取值范围为 .
【变式4-1】如图,平面直角坐标系中,若点A(3,0)、B(4,1)到一次函数y=kx+4(k≠0)图象的距离相等,则k的值为 .
【变式4-2】(2020 成都模拟)在平面直角坐标系xOy中,直线l:y=kx﹣1(k≠0)与直线x=﹣k,y=﹣k分别交于点A,B.直线x=﹣k与y=﹣k交于点C.记线段AB,BC,AC围成的区域(不含边界)为W;横,纵坐标都是整数的点叫做整点.
(1)当k=﹣2时,区域W内的整点个数为 ;
(2)若区域W内没有整点,则k的取值范围是 .
【变式4-3】已知一次函数y=(6+3m)x+(n﹣2).求
(1)当m,n为何值时,y值随x的增大而减小,且与y轴交点在x轴下方?
(2)当m,n为何值时,此一次函数也是正比例函数?
(3)当m=﹣1,n=﹣2时,设此一次函数与x轴交于点A,与y轴交于点B,并求出△AOB的面积(O为坐标原点)
【题型5 一次函数图象上点的坐标特征】
【例5】已知一次函数y=(6+3m)x+(n﹣2).求
(1)当m,n为何值时,y值随x的增大而减小,且与y轴交点在x轴下方?
(2)当m,n为何值时,此一次函数也是正比例函数?
(3)当m=﹣1,n=﹣2时,设此一次函数与x轴交于点A,与y轴交于点B,并求出△AOB的面积(O为坐标原点)
【变式5-1】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BP与x轴相交于P,△ABP的面积是,求点P的坐标.
【变式5-2】如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标(8,0),点A的坐标为(6,0).点P(x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).
(1)求k的值;
(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式.
(3)若△OPA的面积为,求此时点P的坐标.
【变式5-3】(2021春 青县期末)如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.
【题型6 一次函数图象与几何变换】
【例6】已知一次函数y=kx+b的图象过点A(﹣4,﹣2)和点B(2,4)
(1)求直线AB的解析式;
(2)将直线AB平移,使其经过原点O,则线段AB扫过的面积为 .
【变式6-1】若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为( )
A.k=2、b=﹣3 B.k=﹣2、b=﹣3 C.k=﹣2、b=1 D.k=﹣2、b=﹣1
【变式6-2】(2018春 沙坪坝区校级期末)如图:一次函数yx+2交y轴于A,交y=3x﹣6于B,y=3x﹣6交x轴于C,直线BC顺时针旋转45°得到直线CD.
(1)求点B的坐标;
(2)求四边形ABCO的面积;
(3)求直线CD的解析式.
【变式6-3】(2018 沙坪坝区模拟)如图,正比例函数y=kx(k≠0)的图象过点A(2,﹣3).直线y=x+b沿y轴平行移动,与x轴、y轴分别交于点B、C,与直线OA交于点D.
(1)若点D在线段OA上(含端点),求b的取值范围;
(2)当点A关于直线BC的对称点A'恰好落在y轴上时,求△OBD的面积.
一次函数的图象与性质-重难点题型
【知识点1 一次函数与正比例函数的图象】
1、一次函数的图像: 所有一次函数的图像都是一条直线
2、一次函数、正比例函数图像的主要特征:
k的符号 b的符号 函数图像 图像特征
k>0 b>0 图像经过一、二、三象限,y随x的增大而增大。
b<0 图像经过一、三、四象限,y随x的增大而增大。
k<0 b>0 图像经过一、二、四象限,y随x的增大而减小
b<0 图像经过二、三、四象限,y随x的增大而减小。
注:当b=0时,一次函数变为正比例函数,正比例函数是一次函数的特例。
【题型1 一次函数的图象】
【例1】(2021 萧山区模拟)若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=﹣cx﹣a的图象可能是( )
A. B.
C. D.
【解题思路】先判断出a是负数,c是正数,然后根据一次函数图象与系数的关系确定图象经过的象限以及与y轴的交点的位置即可得解.
【解答过程】解:∵a+b+c=0,且a<b<c,
∴a<0,c>0,(b的正负情况不能确定),
∴﹣a>0,﹣c<0,
∴函数y=﹣cx﹣a的图象经过二、一、四象限.
故选:B.
【变式1-1】函数y=ax+b﹣2的图象如图所示,则函数y=﹣ax﹣b的大致图象是( )
A. B. C. D.
【解题思路】根据一次函数的图象的性质确定a和b的符号,进而解答即可.
【解答过程】解:由函数y=ax+b﹣2的图象可得:a<0,b﹣2=0,
∴a<0,b=2>0,
所以函数y=﹣ax﹣b的大致图象经过第一、四、三象限,
故选:C.
【变式1-2】(2019 杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )
A. B.
C. D.
【解题思路】根据直线判断出a、b的符号,然后根据a、b的符号判断出直线经过的象限即可,做出判断.
【解答过程】解:A、由图可知:直线y1=ax+b,a>0,b>0.
∴直线y2=bx+a经过一、二、三象限,故A正确;
B、由图可知:直线y1=ax+b,a<0,b>0.
∴直线y2=bx+a经过一、四、三象限,故B错误;
C、由图可知:直线y1=ax+b,a<0,b>0.
∴直线y2=bx+a经过一、二、四象限,交点不对,故C错误;
D、由图可知:直线y1=ax+b,a<0,b<0,
∴直线y2=bx+a经过二、三、四象限,故D错误.
故选:A.
【变式1-3】函数y=|x﹣2|的图象大致是( )
A. B.
C. D.
【解题思路】由绝对值的性质知,该图象的函数值y≥0,且函数图象经过点(2,0),由此得到正确的函数图象.
【解答过程】解:∵y=|x﹣2|≥0.
∴选项A、D错误.
又∵函数图象经过点(2,0),
∴选项B错误,选项C正确.
故选:C.
【题型2 正比例函数的图象】
【例2】如图,三个正比例函数的图象分别对应函数关系式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为( )
A.a<b<c B.c<a<b C.c<b<a D.a<c<b
【解题思路】根据直线所过象限可得a<0,b>0,c>0,再根据直线陡的情况可判断出b>c,进而得到答案.
【解答过程】解:根据三个函数图象所在象限可得a<0,b>0,c>0,
再根据直线越陡,|k|越大,则b>c.
则b>c>a,
即a<c<b.
故选:D.
【变式2-1】(2020秋 达川区期末)如图,四个一次函数y=ax,y=bx,y=cx+1,y=dx﹣3的图象如图所示,则a,b,c,d的大小关系是( )
A.b>a>d>c B.a>b>c>d C.a>b>d>c D.b>a>c>d
【解题思路】根据一次函数图象的性质分析.
【解答过程】解:由图象可得:a>0,b>0,c<0,d<0,
且a>b,c>d,
故选:B.
【变式2-2】(2021秋 茂名期中)直线y=2kx的图象如图所示,则y=(k﹣2)x+1﹣k的图象大致是( )
A. B.
C. D.
【解题思路】根据正比例函数t=2kx的图象可以判断k的正负,从而可以判断k﹣2与1﹣k的正负,从而可以得到y=(k﹣2)x+1﹣k图象经过哪几个象限,从而可以解答本题.
【解答过程】解:由题意知2k<0,即k<0,
则k﹣2<0,1﹣k>0,
∴y=(k﹣2)x+1﹣k的图象经过第一,二,四象限,
故选:A.
【变式2-3】(2021春 新田县期末)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=3x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn,如果△OA1B1的面积记的作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2021= 4041 .
【解题思路】四边形An﹣1AnBnBn﹣1是梯形,算出梯形的下底AnBn,上底An﹣1Bn﹣1,高是1,取n=2021,用梯形的面积公式即可.
【解答过程】解:由题意得:An(n,n),Bn(n,3n),
∴AnBn=3n﹣n=2n,
同理:An﹣1Bn﹣1=2(n﹣1),
∴,
∴S2021=2×2021﹣1=4041,
故答案为4041.
【知识点2 一次函数与正比例函数的性质】
1.一般地,正比例函数有下列性质:
(1)当k>0时,图像经过第一、三象限,y随x的增大而增大;
(2)当k<0时,图像经过第二、四象限,y随x的增大而减小。
2.一般地,一次函数有下列性质:
(1)当k>0时,y随x的增大而增大
(2)当k<0时,y随x的增大而减小
【题型3 一次函数的性质】
【例3】(2021 萧山区一模)已知y﹣3与x+5成正比例,且当x=﹣2时,y<0,则y关于x的函数图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
【解题思路】由y﹣3与x+5成正比例,可设y﹣3=k(x+5),整理得:y=kx+5k+3.把x=﹣2代入得不等式,可解得k<﹣1,再判断5k+3的符号即可.
【解答过程】解:∵y﹣3与x+5成正比例,
∴设y﹣3=k(x+5),整理得:y=kx+5k+3.
当x=﹣2时,y<0,
即﹣2k+5k+3<0,整理得3k+3<0,
解得:k<﹣1.
∵k<﹣1,
∴5k+3<﹣2,
∴y=kx+5k+3的图象经过第二、三、四象限.
故选:D.
【变式3-1】(2021 黄州区校级自主招生)已知过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,设s=a﹣2b,则s的取值范围是( )
A. B.﹣3<s≤3 C.﹣6<s D.
【解题思路】根据题意得出a>0,b≥0,即可推出得,从而求得s的取值范围.
【解答过程】解:∵过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,
∴a>0,b≥0,
将(2,3)代入直线y=ax+b,
3=2a+b,
b=3﹣2a
∴,
解得,
s=a﹣2b=a﹣2×(3﹣2a)=5a﹣6,
a=0时,s=﹣6,
a,s,
故﹣6<s.
故选:C.
【变式3-2】(2021春 忠县期末)已知一次函数y=(5﹣a)x+a+1的图象不经过第四象限,且关于x的分式方程有整数解,则满足条件的所有整数a的和为( )
A.6 B.7 C.8 D.9
【解题思路】由一次函数y=(5﹣a)x+a+1的图象不经过第四象限求出a的取值范围,把分式方程解出,再根据式方程有整数解,a的取值范围确定a的值,最后算出结果.
【解答过程】解:∵y=(5﹣a)x+a+1的图象不经过第四象限,
∴,
∴﹣1≤a<5.
,
整理得,2,
10=2(2﹣x)+ax,
(2﹣a)x=﹣6,
x,
∵分式方程有整数解,﹣1≤a<5,
∴a=﹣1、0、1、3、4,
∴(﹣1)+0+1+3+4=7.
故选:B.
【变式3-3】(2021 渝中区模拟)若关于x的一元一次不等式组恰有3个整数解,且一次函数y=(a﹣2)x+a+1不经过第三象限,则所有满足条件的整数a的值之和是( )
A.﹣2 B.﹣1 C.0 D.1
【解题思路】根据关于x的一元一次不等式组恰有3个整数解,可以求得a的取值范围,再根据一次函数y=(a﹣2)x+a+1不经过第三象限,可以得到a的取值范围,结合不等式组和一次函数可以得到最后a的取值范围,从而可以写出满足条件的a的整数值,然后相加即可.
【解答过程】解:由不等式组,得x<3,
∵关于x的一元一次不等式组恰有3个整数解,
∴﹣10,
解得﹣3<a≤1,
∵一次函数y=(a﹣2)x+a+1不经过第三象限,
∴a﹣2<0且a+1≥0,
∴﹣1≤a<2,
又∵﹣3<a≤1,
∴﹣1≤a≤1,
∴整数a的值是﹣1,0,1,
∴所有满足条件的整数a的值之和是:﹣1+0+1=0,
故选:C.
【题型4 一次函数图象与系数的关系】
【例4】(2021春 鄢陵县期末)已知A(x1,y1)、B(x2,y2)是一次函数y=(2﹣m)x+3图象上两点,且(x1﹣x2)(y1﹣y2)<0,则m的取值范围为 m>2 .
【解题思路】根据(x1﹣x2)(y1﹣y2)<0,得出y随x的增大而减小,再根据2﹣m<0,求出其取值范围即可.
【解答过程】解:(x1﹣x2)(y1﹣y2)<0,
即:或,
也就是,y随x的增大而减小,
因此,2﹣m<0,解得,m>2,
故答案为:m>2.
【变式4-1】如图,平面直角坐标系中,若点A(3,0)、B(4,1)到一次函数y=kx+4(k≠0)图象的距离相等,则k的值为 k=±1 .
【解题思路】根据一次函数y=kx+4(k≠0)图象一定过点(0,4),点A(3,0)、B(4,1)到一次函数y=kx+4(k≠0)图象的距离相等,可分为两种情况进行解答,即,
①当直线y=kx+4(k≠0)与直线AB平行时,②当直线y=kx+4(k≠0)与直线AB不平行时分别进行解答即可.
【解答过程】解:一次函数y=kx+4(k≠0)图象一定过(0,4)点,
①当直线y=kx+4(k≠0)与直线AB平行时,如图1,
设直线AB的关系式为y=kx+b,
把A(3,0),B(4,1)代入得,
,解得,k=1,b=﹣3,
∴一次函数y=kx+4(k≠0)中的k=1,
②当直线y=kx+4(k≠0)与直线AB不平行时,如图2,
则:直线y=kx+4(k≠0)一定过点C,点C的坐标为(4,0),代入得,
4k+4=0,解得,k=﹣1,
因此,k=1或k=﹣1.
故答案为:k=±1.
【变式4-2】(2020 成都模拟)在平面直角坐标系xOy中,直线l:y=kx﹣1(k≠0)与直线x=﹣k,y=﹣k分别交于点A,B.直线x=﹣k与y=﹣k交于点C.记线段AB,BC,AC围成的区域(不含边界)为W;横,纵坐标都是整数的点叫做整点.
(1)当k=﹣2时,区域W内的整点个数为 6 ;
(2)若区域W内没有整点,则k的取值范围是 0<k≤1或k=2 .
【解题思路】(1)将k=﹣2代入解析式,求得A、B、C三点坐标,并作出图形,便可求得W区域内的整数点个数;
(2)分三种情况解答:当k<0时,区域内必含有坐标原点,故不符合题意;当0<k≤1时,W内点的横坐标在k到0之间,无整点,进而得0<k≤1时,W内无整点;当1<k≤2时,W内可能存在的整数点横坐标只能为﹣1,此时边界上两点坐标为(﹣1,﹣k)和(﹣1,﹣k﹣1),当k不为整数时,其上必有整点,但k=2时,只有两个边界点为整点,故W内无整点;当k>2时,横坐标为﹣2的边界点为(﹣2,﹣k)和(﹣2,﹣2k﹣1),线段长度为k+1>3,故必有整点.
【解答过程】解:(1)直线l:y=kx﹣1=﹣2x﹣1,直线x=﹣k=2,y=﹣k=2,
∴A(2,﹣5),B(,2),C(2,2),
在W区域内有6个整数点:(0,0),(0,1),(1,0),(1,1),(1,﹣1),(1,﹣2),
故答案为6;
(2)当k<0时,则x=﹣k>0,y=﹣k>0,
∴区域内必含有坐标原点,故不符合题意;
当0<k≤1时,W内点的横坐标在﹣1到0之间,不存在整点,故0<k≤1时W内无整点;
当1<k≤2时,W内可能存在的整数点横坐标只能为﹣1,此时边界上两点坐标为M(﹣1,﹣k)和N(﹣1,﹣k﹣1),MN=1,此时当k不为整数时,其上必有整点,但k=2时,只有两个边界点为整点,故W内无整点;
当k>2时,横坐标为﹣2的边界点为(﹣2,﹣k)和(﹣2,﹣2k﹣1),线段长度为k+1>3,故必有整点.
综上所述:0<k≤1或k=2时,W内没有整点.
故答案为:0<k≤1或k=2.
【变式4-3】已知一次函数y=(6+3m)x+(n﹣2).求
(1)当m,n为何值时,y值随x的增大而减小,且与y轴交点在x轴下方?
(2)当m,n为何值时,此一次函数也是正比例函数?
(3)当m=﹣1,n=﹣2时,设此一次函数与x轴交于点A,与y轴交于点B,并求出△AOB的面积(O为坐标原点)
【解题思路】(1)根据一次函数的性质结合一次函数单调递减,即可得出关于m、n的一元一次不等式,解不等式即可得出m、n的取值范围;
(2)由此一次函数也是正比例函数,可得出关于m、n的一元一次方程,解方程即可得出结论;
(3)代入m、n的值,再根据一次函数图象上点的坐标特征找出点A、B的坐标,利用三角形的面积公式即可得出结论.
【解答过程】解:(1)∵y值随x的增大而减小,且与y轴交点在x轴下方,
∴6+3m<0,解得m<﹣2,
n﹣2<0,解得n<2;
(2)∵此一次函数也是正比例函数,
∴n﹣2=0且6+3m≠0,
解得n=2且m≠﹣2;
(3)当m=﹣1,n=﹣2时,一次函数的解析式为y=3x﹣4,
当x=0时,y=﹣4,
∴点B的坐标为(0,﹣4);
当y=0时,x,
∴点A的坐标为(,0).
∴S△AOBOA OB4.
【题型5 一次函数图象上点的坐标特征】
【例5】已知一次函数y=(6+3m)x+(n﹣2).求
(1)当m,n为何值时,y值随x的增大而减小,且与y轴交点在x轴下方?
(2)当m,n为何值时,此一次函数也是正比例函数?
(3)当m=﹣1,n=﹣2时,设此一次函数与x轴交于点A,与y轴交于点B,并求出△AOB的面积(O为坐标原点)
【解题思路】(1)根据一次函数的性质结合一次函数单调递减,即可得出关于m、n的一元一次不等式,解不等式即可得出m、n的取值范围;
(2)由此一次函数也是正比例函数,可得出关于m、n的一元一次方程,解方程即可得出结论;
(3)代入m、n的值,再根据一次函数图象上点的坐标特征找出点A、B的坐标,利用三角形的面积公式即可得出结论.
【解答过程】解:(1)∵y值随x的增大而减小,且与y轴交点在x轴下方,
∴6+3m<0,解得m<﹣2,
n﹣2<0,解得n<2;
(2)∵此一次函数也是正比例函数,
∴n﹣2=0且6+3m≠0,
解得n=2且m≠﹣2;
(3)当m=﹣1,n=﹣2时,一次函数的解析式为y=3x﹣4,
当x=0时,y=﹣4,
∴点B的坐标为(0,﹣4);
当y=0时,x,
∴点A的坐标为(,0).
∴S△AOBOA OB4.
【变式5-1】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BP与x轴相交于P,△ABP的面积是,求点P的坐标.
【解题思路】(1)把x=0,y=0分别代入函数解析式,即可求得相应的y、x的值,则易得点OA、OB的值,然后根据三角形面积公式求得即可;
(2)由B、A的坐标易求:OB=3,OA.然后由三角形面积公式得到S△ABPAP OB,则AP=3,由此可以求得m的值
【解答过程】解:(1)由x=0得:y=3,即:B(0,3).
由y=0得:2x+3=0,解得:x,即:A(,0),
∴OA,OB=3,
∴△AOB的面积:3;
(2)由B(0,3)、A(,0)得:OB=3,OA,
∵S△ABPAP OB,
∴AP,
解得:AP=3.
∴P点坐标为(1.5,0)或(﹣4.5,0).
【变式5-2】如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标(8,0),点A的坐标为(6,0).点P(x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).
(1)求k的值;
(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式.
(3)若△OPA的面积为,求此时点P的坐标.
【解题思路】(1)直接把点E的坐标代入直线y=kx+6求出k的值即可;
(2)过点P作PD⊥OA于点D,用x表示出PD的长,根据三角形的面积公式即可得出结论;
(3)把△OPA的面积为代入(2)中关系式,求出x的值,把x的值代入直线yx+6即可得出结论.
【解答过程】解:(1)∵直线y=kx+6与x轴交于点E,且点E的坐标(8,0)
∴8k+6=0,
解得k,
∴yx+6;
(2)过点P作PD⊥OA于点D,
∵点P(x,y)是第一象限内的直线上的一个动点
∴PDx+6.
∵点A的坐标为(6,0)
∴S6×(x+6)
x+18;
(3)∵△OPA的面积为,
∴x+18,
解得x,
将x代入yx+6得y,
∴P(,).
【变式5-3】(2021春 青县期末)如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.
【解题思路】(1)根据三角形的面积公式S△OPAOA y,然后把y转换成x,即可求得△OPA的面积S与x的函数关系式;
(2)把s=10代入S=﹣4x+40,求得x的值,把x的值代入y=﹣x+10即可求得P的坐标.
【解答过程】解(1)∵A(8,0),
∴OA=8,
SOA |yP|8×(﹣x+10)=﹣4x+40,(0<x<10).
(2)当S=10时,则﹣4x+40=10,解得x,
当x时,y10,
∴当△OPA的面积为10时,点P的坐标为(,).
【题型6 一次函数图象与几何变换】
【例6】已知一次函数y=kx+b的图象过点A(﹣4,﹣2)和点B(2,4)
(1)求直线AB的解析式;
(2)将直线AB平移,使其经过原点O,则线段AB扫过的面积为 12 .
【解题思路】(1)将A、B两点的坐标代入y=kx+b,利用待定系数法即可求出直线AB的解析式;
(2)先利用平移规律求出直线AB平移后的解析式,进而求出线段AB扫过的面积.
【解答过程】解:(1)∵一次函数y=kx+b的图象过点A(﹣4,﹣2)和点B(2,4),
∴,解得,
∴直线AB的解析式为y=x+2;
(2)设直线AB平移后的解析式为y=x+n,
将原点(0,0)代入,得n=0,
∴直线AB平移后的解析式为y=x,
∴将直线AB向下平移2个单位得到直线A′B′,
如图,则A′(﹣4,﹣4),B′(2,2),
∴平行四边形AA′B′B的面积=2×(4+2)=12.
即线段AB扫过的面积为12.
故答案为12.
【变式6-1】若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为( )
A.k=2、b=﹣3 B.k=﹣2、b=﹣3 C.k=﹣2、b=1 D.k=﹣2、b=﹣1
【解题思路】先求出一次函数y=kx+3与y轴交点关于直线x=1的对称点,得到b的值,再求出一次函数y=2x+b与y轴交点关于直线x=1的对称点,代入一次函数y=kx+3,求出k的值即可.
【解答过程】解:∵一次函数y=kx+3与y轴交点为(0,3),
∴点(0,3)关于直线x=1的对称点为(2,3),
代入直线y=2x+b,可得
4+b=3,
解得b=﹣1,
一次函数y=2x﹣1与y轴交点为(0,﹣1),
(0,﹣1)关于直线x=1的对称点为(2,﹣1),
代入直线y=kx+3,可得
2k+3=﹣1,
解得k=﹣2.
故选:D.
【变式6-2】(2018春 沙坪坝区校级期末)如图:一次函数yx+2交y轴于A,交y=3x﹣6于B,y=3x﹣6交x轴于C,直线BC顺时针旋转45°得到直线CD.
(1)求点B的坐标;
(2)求四边形ABCO的面积;
(3)求直线CD的解析式.
【解题思路】(1)构建方程组即可解决问题;
(2)求出A、C两点坐标,根据S四边形ABCO=S△OCB+S△AOB计算即可;
(3)如图,将线段BC绕点B逆时针旋转90得到C′.由题意可知点C′在直线CD上,求出点C′坐标,利用待定系数法即可解决问题;
【解答过程】解:(1)由,解得,
∴B(3,3).
(2)由题意A(0,2),C(2,0),
∴S四边形ABCO=S△OCB+S△AOB2×32×3=6.
(3)如图,将线段BC绕点B逆时针旋转90得到C′.
∵△BCC′是等腰直角三角形,∠BCD=45°,
∴点C′在直线CD上,
由(2)可知,C(2,0).
∵B(3,3),
由旋转的性质可知,C′(6,2),
设直线CD的解析式为y=kx+b,则有,
解得,
∴直线CD的解析式为yx﹣1.
【变式6-3】(2018 沙坪坝区模拟)如图,正比例函数y=kx(k≠0)的图象过点A(2,﹣3).直线y=x+b沿y轴平行移动,与x轴、y轴分别交于点B、C,与直线OA交于点D.
(1)若点D在线段OA上(含端点),求b的取值范围;
(2)当点A关于直线BC的对称点A'恰好落在y轴上时,求△OBD的面积.
【解题思路】(1)将O点和A点的坐标分别代入y=x+b,即可求得b的值,从而求得b的取值范围;
(2)根据直线y=x+b易求得OB=OC,即可得出∠OCB=45°,根据轴对称的性质易求得∠ACD=45°.即可求得∠ACO=90°,从而求得C的纵坐标为﹣3,得出C的坐标为(0,﹣3),即可求得直线y=x﹣3,然后联立方程求得交点D的坐标,根据三角形面积公式即可求得△OBD的面积.
【解答过程】解:(1)当点D和点O重合时,
将点O(0,0)代入y=x+b中,得b=0,
当点D和点A重合时,
将点A(2,﹣3)代入y=x+b中,得﹣3=2+b,即b=﹣5,
∴b的取值范围是﹣5≤b≤0;
(2)将点A(2,﹣3)代入y=kx中,得﹣3=2k,即k,
∴直线OA的解析式为yx,
在y=x+b中,令y=0,则x=﹣b,
∴B(﹣b,0),即OB=|b|,
∴OB=OC,
又∵∠BOC=90°,
∴∠OCB=∠OBC=45°,
∵点A关于直线BC的对称点A'恰好落在y轴上,
∴CD垂直平分AA′,
∴CA=CA′,
∴∠ACD=∠OCB=45°,
∴∠ACO=90°,
∴OC=|yA|=3,
∴OB=OC=3,即C(0,﹣3),
将点C(0,﹣3)代入y=x+b中,得﹣3=0+b,
∴b=﹣3,
∴直线BC的解析式为y=x﹣3,
由得,
∴D(,),
∴S△OBDOB |yD|3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
一次函数的图象与性质6大题型
【知识点1 一次函数与正比例函数的图象】
1、一次函数的图像: 所有一次函数的图像都是一条直线
2、一次函数、正比例函数图像的主要特征:
k的符号 b的符号 函数图像 图像特征
k>0 b>0 图像经过一、二、三象限,y随x的增大而增大。
b<0 图像经过一、三、四象限,y随x的增大而增大。
k<0 b>0 图像经过一、二、四象限,y随x的增大而减小
b<0 图像经过二、三、四象限,y随x的增大而减小。
注:当b=0时,一次函数变为正比例函数,正比例函数是一次函数的特例。
【题型1 一次函数的图象】
【例1】(2021 萧山区模拟)若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=﹣cx﹣a的图象可能是( )
A. B.
C. D.
【变式1-1】函数y=ax+b﹣2的图象如图所示,则函数y=﹣ax﹣b的大致图象是( )
A. B. C. D.
【变式1-2】(2019 杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )
A. B.
C. D.
【变式1-3】函数y=|x﹣2|的图象大致是( )
A. B.
C. D.
【题型2 正比例函数的图象】
【例2】如图,三个正比例函数的图象分别对应函数关系式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为( )
A.a<b<c B.c<a<b C.c<b<a D.a<c<b
【变式2-1】(2020秋 达川区期末)如图,四个一次函数y=ax,y=bx,y=cx+1,y=dx﹣3的图象如图所示,则a,b,c,d的大小关系是( )
A.b>a>d>c B.a>b>c>d C.a>b>d>c D.b>a>c>d
【变式2-2】(2021秋 茂名期中)直线y=2kx的图象如图所示,则y=(k﹣2)x+1﹣k的图象大致是( )
A. B.
C. D.
【变式2-3】(2021春 新田县期末)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=3x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn,如果△OA1B1的面积记的作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2021= .
.
【知识点2 一次函数与正比例函数的性质】
1.一般地,正比例函数有下列性质:
(1)当k>0时,图像经过第一、三象限,y随x的增大而增大;
(2)当k<0时,图像经过第二、四象限,y随x的增大而减小。
2.一般地,一次函数有下列性质:
(1)当k>0时,y随x的增大而增大
(2)当k<0时,y随x的增大而减小
【题型3 一次函数的性质】
【例3】(2021 萧山区一模)已知y﹣3与x+5成正比例,且当x=﹣2时,y<0,则y关于x的函数图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
【变式3-1】(2021 黄州区校级自主招生)已知过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,设s=a﹣2b,则s的取值范围是( )
A. B.﹣3<s≤3 C.﹣6<s D.
【变式3-2】(2021春 忠县期末)已知一次函数y=(5﹣a)x+a+1的图象不经过第四象限,且关于x的分式方程有整数解,则满足条件的所有整数a的和为( )
A.6 B.7 C.8 D.9
【变式3-3】(2021 渝中区模拟)若关于x的一元一次不等式组恰有3个整数解,且一次函数y=(a﹣2)x+a+1不经过第三象限,则所有满足条件的整数a的值之和是( )
A.﹣2 B.﹣1 C.0 D.1
【题型4 一次函数图象与系数的关系】
【例4】(2021春 鄢陵县期末)已知A(x1,y1)、B(x2,y2)是一次函数y=(2﹣m)x+3图象上两点,且(x1﹣x2)(y1﹣y2)<0,则m的取值范围为 .
【变式4-1】如图,平面直角坐标系中,若点A(3,0)、B(4,1)到一次函数y=kx+4(k≠0)图象的距离相等,则k的值为 .
【变式4-2】(2020 成都模拟)在平面直角坐标系xOy中,直线l:y=kx﹣1(k≠0)与直线x=﹣k,y=﹣k分别交于点A,B.直线x=﹣k与y=﹣k交于点C.记线段AB,BC,AC围成的区域(不含边界)为W;横,纵坐标都是整数的点叫做整点.
(1)当k=﹣2时,区域W内的整点个数为 ;
(2)若区域W内没有整点,则k的取值范围是 .
【变式4-3】已知一次函数y=(6+3m)x+(n﹣2).求
(1)当m,n为何值时,y值随x的增大而减小,且与y轴交点在x轴下方?
(2)当m,n为何值时,此一次函数也是正比例函数?
(3)当m=﹣1,n=﹣2时,设此一次函数与x轴交于点A,与y轴交于点B,并求出△AOB的面积(O为坐标原点)
【题型5 一次函数图象上点的坐标特征】
【例5】已知一次函数y=(6+3m)x+(n﹣2).求
(1)当m,n为何值时,y值随x的增大而减小,且与y轴交点在x轴下方?
(2)当m,n为何值时,此一次函数也是正比例函数?
(3)当m=﹣1,n=﹣2时,设此一次函数与x轴交于点A,与y轴交于点B,并求出△AOB的面积(O为坐标原点)
【变式5-1】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BP与x轴相交于P,△ABP的面积是,求点P的坐标.
【变式5-2】如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标(8,0),点A的坐标为(6,0).点P(x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).
(1)求k的值;
(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式.
(3)若△OPA的面积为,求此时点P的坐标.
【变式5-3】(2021春 青县期末)如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.
【题型6 一次函数图象与几何变换】
【例6】已知一次函数y=kx+b的图象过点A(﹣4,﹣2)和点B(2,4)
(1)求直线AB的解析式;
(2)将直线AB平移,使其经过原点O,则线段AB扫过的面积为 .
【变式6-1】若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为( )
A.k=2、b=﹣3 B.k=﹣2、b=﹣3 C.k=﹣2、b=1 D.k=﹣2、b=﹣1
【变式6-2】(2018春 沙坪坝区校级期末)如图:一次函数yx+2交y轴于A,交y=3x﹣6于B,y=3x﹣6交x轴于C,直线BC顺时针旋转45°得到直线CD.
(1)求点B的坐标;
(2)求四边形ABCO的面积;
(3)求直线CD的解析式.
【变式6-3】(2018 沙坪坝区模拟)如图,正比例函数y=kx(k≠0)的图象过点A(2,﹣3).直线y=x+b沿y轴平行移动,与x轴、y轴分别交于点B、C,与直线OA交于点D.
(1)若点D在线段OA上(含端点),求b的取值范围;
(2)当点A关于直线BC的对称点A'恰好落在y轴上时,求△OBD的面积.
一次函数的图象与性质-重难点题型
【知识点1 一次函数与正比例函数的图象】
1、一次函数的图像: 所有一次函数的图像都是一条直线
2、一次函数、正比例函数图像的主要特征:
k的符号 b的符号 函数图像 图像特征
k>0 b>0 图像经过一、二、三象限,y随x的增大而增大。
b<0 图像经过一、三、四象限,y随x的增大而增大。
k<0 b>0 图像经过一、二、四象限,y随x的增大而减小
b<0 图像经过二、三、四象限,y随x的增大而减小。
注:当b=0时,一次函数变为正比例函数,正比例函数是一次函数的特例。
【题型1 一次函数的图象】
【例1】(2021 萧山区模拟)若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=﹣cx﹣a的图象可能是( )
A. B.
C. D.
【解题思路】先判断出a是负数,c是正数,然后根据一次函数图象与系数的关系确定图象经过的象限以及与y轴的交点的位置即可得解.
【解答过程】解:∵a+b+c=0,且a<b<c,
∴a<0,c>0,(b的正负情况不能确定),
∴﹣a>0,﹣c<0,
∴函数y=﹣cx﹣a的图象经过二、一、四象限.
故选:B.
【变式1-1】函数y=ax+b﹣2的图象如图所示,则函数y=﹣ax﹣b的大致图象是( )
A. B. C. D.
【解题思路】根据一次函数的图象的性质确定a和b的符号,进而解答即可.
【解答过程】解:由函数y=ax+b﹣2的图象可得:a<0,b﹣2=0,
∴a<0,b=2>0,
所以函数y=﹣ax﹣b的大致图象经过第一、四、三象限,
故选:C.
【变式1-2】(2019 杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )
A. B.
C. D.
【解题思路】根据直线判断出a、b的符号,然后根据a、b的符号判断出直线经过的象限即可,做出判断.
【解答过程】解:A、由图可知:直线y1=ax+b,a>0,b>0.
∴直线y2=bx+a经过一、二、三象限,故A正确;
B、由图可知:直线y1=ax+b,a<0,b>0.
∴直线y2=bx+a经过一、四、三象限,故B错误;
C、由图可知:直线y1=ax+b,a<0,b>0.
∴直线y2=bx+a经过一、二、四象限,交点不对,故C错误;
D、由图可知:直线y1=ax+b,a<0,b<0,
∴直线y2=bx+a经过二、三、四象限,故D错误.
故选:A.
【变式1-3】函数y=|x﹣2|的图象大致是( )
A. B.
C. D.
【解题思路】由绝对值的性质知,该图象的函数值y≥0,且函数图象经过点(2,0),由此得到正确的函数图象.
【解答过程】解:∵y=|x﹣2|≥0.
∴选项A、D错误.
又∵函数图象经过点(2,0),
∴选项B错误,选项C正确.
故选:C.
【题型2 正比例函数的图象】
【例2】如图,三个正比例函数的图象分别对应函数关系式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为( )
A.a<b<c B.c<a<b C.c<b<a D.a<c<b
【解题思路】根据直线所过象限可得a<0,b>0,c>0,再根据直线陡的情况可判断出b>c,进而得到答案.
【解答过程】解:根据三个函数图象所在象限可得a<0,b>0,c>0,
再根据直线越陡,|k|越大,则b>c.
则b>c>a,
即a<c<b.
故选:D.
【变式2-1】(2020秋 达川区期末)如图,四个一次函数y=ax,y=bx,y=cx+1,y=dx﹣3的图象如图所示,则a,b,c,d的大小关系是( )
A.b>a>d>c B.a>b>c>d C.a>b>d>c D.b>a>c>d
【解题思路】根据一次函数图象的性质分析.
【解答过程】解:由图象可得:a>0,b>0,c<0,d<0,
且a>b,c>d,
故选:B.
【变式2-2】(2021秋 茂名期中)直线y=2kx的图象如图所示,则y=(k﹣2)x+1﹣k的图象大致是( )
A. B.
C. D.
【解题思路】根据正比例函数t=2kx的图象可以判断k的正负,从而可以判断k﹣2与1﹣k的正负,从而可以得到y=(k﹣2)x+1﹣k图象经过哪几个象限,从而可以解答本题.
【解答过程】解:由题意知2k<0,即k<0,
则k﹣2<0,1﹣k>0,
∴y=(k﹣2)x+1﹣k的图象经过第一,二,四象限,
故选:A.
【变式2-3】(2021春 新田县期末)如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=3x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn,如果△OA1B1的面积记的作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2021= 4041 .
【解题思路】四边形An﹣1AnBnBn﹣1是梯形,算出梯形的下底AnBn,上底An﹣1Bn﹣1,高是1,取n=2021,用梯形的面积公式即可.
【解答过程】解:由题意得:An(n,n),Bn(n,3n),
∴AnBn=3n﹣n=2n,
同理:An﹣1Bn﹣1=2(n﹣1),
∴,
∴S2021=2×2021﹣1=4041,
故答案为4041.
【知识点2 一次函数与正比例函数的性质】
1.一般地,正比例函数有下列性质:
(1)当k>0时,图像经过第一、三象限,y随x的增大而增大;
(2)当k<0时,图像经过第二、四象限,y随x的增大而减小。
2.一般地,一次函数有下列性质:
(1)当k>0时,y随x的增大而增大
(2)当k<0时,y随x的增大而减小
【题型3 一次函数的性质】
【例3】(2021 萧山区一模)已知y﹣3与x+5成正比例,且当x=﹣2时,y<0,则y关于x的函数图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
【解题思路】由y﹣3与x+5成正比例,可设y﹣3=k(x+5),整理得:y=kx+5k+3.把x=﹣2代入得不等式,可解得k<﹣1,再判断5k+3的符号即可.
【解答过程】解:∵y﹣3与x+5成正比例,
∴设y﹣3=k(x+5),整理得:y=kx+5k+3.
当x=﹣2时,y<0,
即﹣2k+5k+3<0,整理得3k+3<0,
解得:k<﹣1.
∵k<﹣1,
∴5k+3<﹣2,
∴y=kx+5k+3的图象经过第二、三、四象限.
故选:D.
【变式3-1】(2021 黄州区校级自主招生)已知过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,设s=a﹣2b,则s的取值范围是( )
A. B.﹣3<s≤3 C.﹣6<s D.
【解题思路】根据题意得出a>0,b≥0,即可推出得,从而求得s的取值范围.
【解答过程】解:∵过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,
∴a>0,b≥0,
将(2,3)代入直线y=ax+b,
3=2a+b,
b=3﹣2a
∴,
解得,
s=a﹣2b=a﹣2×(3﹣2a)=5a﹣6,
a=0时,s=﹣6,
a,s,
故﹣6<s.
故选:C.
【变式3-2】(2021春 忠县期末)已知一次函数y=(5﹣a)x+a+1的图象不经过第四象限,且关于x的分式方程有整数解,则满足条件的所有整数a的和为( )
A.6 B.7 C.8 D.9
【解题思路】由一次函数y=(5﹣a)x+a+1的图象不经过第四象限求出a的取值范围,把分式方程解出,再根据式方程有整数解,a的取值范围确定a的值,最后算出结果.
【解答过程】解:∵y=(5﹣a)x+a+1的图象不经过第四象限,
∴,
∴﹣1≤a<5.
,
整理得,2,
10=2(2﹣x)+ax,
(2﹣a)x=﹣6,
x,
∵分式方程有整数解,﹣1≤a<5,
∴a=﹣1、0、1、3、4,
∴(﹣1)+0+1+3+4=7.
故选:B.
【变式3-3】(2021 渝中区模拟)若关于x的一元一次不等式组恰有3个整数解,且一次函数y=(a﹣2)x+a+1不经过第三象限,则所有满足条件的整数a的值之和是( )
A.﹣2 B.﹣1 C.0 D.1
【解题思路】根据关于x的一元一次不等式组恰有3个整数解,可以求得a的取值范围,再根据一次函数y=(a﹣2)x+a+1不经过第三象限,可以得到a的取值范围,结合不等式组和一次函数可以得到最后a的取值范围,从而可以写出满足条件的a的整数值,然后相加即可.
【解答过程】解:由不等式组,得x<3,
∵关于x的一元一次不等式组恰有3个整数解,
∴﹣10,
解得﹣3<a≤1,
∵一次函数y=(a﹣2)x+a+1不经过第三象限,
∴a﹣2<0且a+1≥0,
∴﹣1≤a<2,
又∵﹣3<a≤1,
∴﹣1≤a≤1,
∴整数a的值是﹣1,0,1,
∴所有满足条件的整数a的值之和是:﹣1+0+1=0,
故选:C.
【题型4 一次函数图象与系数的关系】
【例4】(2021春 鄢陵县期末)已知A(x1,y1)、B(x2,y2)是一次函数y=(2﹣m)x+3图象上两点,且(x1﹣x2)(y1﹣y2)<0,则m的取值范围为 m>2 .
【解题思路】根据(x1﹣x2)(y1﹣y2)<0,得出y随x的增大而减小,再根据2﹣m<0,求出其取值范围即可.
【解答过程】解:(x1﹣x2)(y1﹣y2)<0,
即:或,
也就是,y随x的增大而减小,
因此,2﹣m<0,解得,m>2,
故答案为:m>2.
【变式4-1】如图,平面直角坐标系中,若点A(3,0)、B(4,1)到一次函数y=kx+4(k≠0)图象的距离相等,则k的值为 k=±1 .
【解题思路】根据一次函数y=kx+4(k≠0)图象一定过点(0,4),点A(3,0)、B(4,1)到一次函数y=kx+4(k≠0)图象的距离相等,可分为两种情况进行解答,即,
①当直线y=kx+4(k≠0)与直线AB平行时,②当直线y=kx+4(k≠0)与直线AB不平行时分别进行解答即可.
【解答过程】解:一次函数y=kx+4(k≠0)图象一定过(0,4)点,
①当直线y=kx+4(k≠0)与直线AB平行时,如图1,
设直线AB的关系式为y=kx+b,
把A(3,0),B(4,1)代入得,
,解得,k=1,b=﹣3,
∴一次函数y=kx+4(k≠0)中的k=1,
②当直线y=kx+4(k≠0)与直线AB不平行时,如图2,
则:直线y=kx+4(k≠0)一定过点C,点C的坐标为(4,0),代入得,
4k+4=0,解得,k=﹣1,
因此,k=1或k=﹣1.
故答案为:k=±1.
【变式4-2】(2020 成都模拟)在平面直角坐标系xOy中,直线l:y=kx﹣1(k≠0)与直线x=﹣k,y=﹣k分别交于点A,B.直线x=﹣k与y=﹣k交于点C.记线段AB,BC,AC围成的区域(不含边界)为W;横,纵坐标都是整数的点叫做整点.
(1)当k=﹣2时,区域W内的整点个数为 6 ;
(2)若区域W内没有整点,则k的取值范围是 0<k≤1或k=2 .
【解题思路】(1)将k=﹣2代入解析式,求得A、B、C三点坐标,并作出图形,便可求得W区域内的整数点个数;
(2)分三种情况解答:当k<0时,区域内必含有坐标原点,故不符合题意;当0<k≤1时,W内点的横坐标在k到0之间,无整点,进而得0<k≤1时,W内无整点;当1<k≤2时,W内可能存在的整数点横坐标只能为﹣1,此时边界上两点坐标为(﹣1,﹣k)和(﹣1,﹣k﹣1),当k不为整数时,其上必有整点,但k=2时,只有两个边界点为整点,故W内无整点;当k>2时,横坐标为﹣2的边界点为(﹣2,﹣k)和(﹣2,﹣2k﹣1),线段长度为k+1>3,故必有整点.
【解答过程】解:(1)直线l:y=kx﹣1=﹣2x﹣1,直线x=﹣k=2,y=﹣k=2,
∴A(2,﹣5),B(,2),C(2,2),
在W区域内有6个整数点:(0,0),(0,1),(1,0),(1,1),(1,﹣1),(1,﹣2),
故答案为6;
(2)当k<0时,则x=﹣k>0,y=﹣k>0,
∴区域内必含有坐标原点,故不符合题意;
当0<k≤1时,W内点的横坐标在﹣1到0之间,不存在整点,故0<k≤1时W内无整点;
当1<k≤2时,W内可能存在的整数点横坐标只能为﹣1,此时边界上两点坐标为M(﹣1,﹣k)和N(﹣1,﹣k﹣1),MN=1,此时当k不为整数时,其上必有整点,但k=2时,只有两个边界点为整点,故W内无整点;
当k>2时,横坐标为﹣2的边界点为(﹣2,﹣k)和(﹣2,﹣2k﹣1),线段长度为k+1>3,故必有整点.
综上所述:0<k≤1或k=2时,W内没有整点.
故答案为:0<k≤1或k=2.
【变式4-3】已知一次函数y=(6+3m)x+(n﹣2).求
(1)当m,n为何值时,y值随x的增大而减小,且与y轴交点在x轴下方?
(2)当m,n为何值时,此一次函数也是正比例函数?
(3)当m=﹣1,n=﹣2时,设此一次函数与x轴交于点A,与y轴交于点B,并求出△AOB的面积(O为坐标原点)
【解题思路】(1)根据一次函数的性质结合一次函数单调递减,即可得出关于m、n的一元一次不等式,解不等式即可得出m、n的取值范围;
(2)由此一次函数也是正比例函数,可得出关于m、n的一元一次方程,解方程即可得出结论;
(3)代入m、n的值,再根据一次函数图象上点的坐标特征找出点A、B的坐标,利用三角形的面积公式即可得出结论.
【解答过程】解:(1)∵y值随x的增大而减小,且与y轴交点在x轴下方,
∴6+3m<0,解得m<﹣2,
n﹣2<0,解得n<2;
(2)∵此一次函数也是正比例函数,
∴n﹣2=0且6+3m≠0,
解得n=2且m≠﹣2;
(3)当m=﹣1,n=﹣2时,一次函数的解析式为y=3x﹣4,
当x=0时,y=﹣4,
∴点B的坐标为(0,﹣4);
当y=0时,x,
∴点A的坐标为(,0).
∴S△AOBOA OB4.
【题型5 一次函数图象上点的坐标特征】
【例5】已知一次函数y=(6+3m)x+(n﹣2).求
(1)当m,n为何值时,y值随x的增大而减小,且与y轴交点在x轴下方?
(2)当m,n为何值时,此一次函数也是正比例函数?
(3)当m=﹣1,n=﹣2时,设此一次函数与x轴交于点A,与y轴交于点B,并求出△AOB的面积(O为坐标原点)
【解题思路】(1)根据一次函数的性质结合一次函数单调递减,即可得出关于m、n的一元一次不等式,解不等式即可得出m、n的取值范围;
(2)由此一次函数也是正比例函数,可得出关于m、n的一元一次方程,解方程即可得出结论;
(3)代入m、n的值,再根据一次函数图象上点的坐标特征找出点A、B的坐标,利用三角形的面积公式即可得出结论.
【解答过程】解:(1)∵y值随x的增大而减小,且与y轴交点在x轴下方,
∴6+3m<0,解得m<﹣2,
n﹣2<0,解得n<2;
(2)∵此一次函数也是正比例函数,
∴n﹣2=0且6+3m≠0,
解得n=2且m≠﹣2;
(3)当m=﹣1,n=﹣2时,一次函数的解析式为y=3x﹣4,
当x=0时,y=﹣4,
∴点B的坐标为(0,﹣4);
当y=0时,x,
∴点A的坐标为(,0).
∴S△AOBOA OB4.
【变式5-1】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BP与x轴相交于P,△ABP的面积是,求点P的坐标.
【解题思路】(1)把x=0,y=0分别代入函数解析式,即可求得相应的y、x的值,则易得点OA、OB的值,然后根据三角形面积公式求得即可;
(2)由B、A的坐标易求:OB=3,OA.然后由三角形面积公式得到S△ABPAP OB,则AP=3,由此可以求得m的值
【解答过程】解:(1)由x=0得:y=3,即:B(0,3).
由y=0得:2x+3=0,解得:x,即:A(,0),
∴OA,OB=3,
∴△AOB的面积:3;
(2)由B(0,3)、A(,0)得:OB=3,OA,
∵S△ABPAP OB,
∴AP,
解得:AP=3.
∴P点坐标为(1.5,0)或(﹣4.5,0).
【变式5-2】如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标(8,0),点A的坐标为(6,0).点P(x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).
(1)求k的值;
(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式.
(3)若△OPA的面积为,求此时点P的坐标.
【解题思路】(1)直接把点E的坐标代入直线y=kx+6求出k的值即可;
(2)过点P作PD⊥OA于点D,用x表示出PD的长,根据三角形的面积公式即可得出结论;
(3)把△OPA的面积为代入(2)中关系式,求出x的值,把x的值代入直线yx+6即可得出结论.
【解答过程】解:(1)∵直线y=kx+6与x轴交于点E,且点E的坐标(8,0)
∴8k+6=0,
解得k,
∴yx+6;
(2)过点P作PD⊥OA于点D,
∵点P(x,y)是第一象限内的直线上的一个动点
∴PDx+6.
∵点A的坐标为(6,0)
∴S6×(x+6)
x+18;
(3)∵△OPA的面积为,
∴x+18,
解得x,
将x代入yx+6得y,
∴P(,).
【变式5-3】(2021春 青县期末)如图,直线y=﹣x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=﹣x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量的x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.
【解题思路】(1)根据三角形的面积公式S△OPAOA y,然后把y转换成x,即可求得△OPA的面积S与x的函数关系式;
(2)把s=10代入S=﹣4x+40,求得x的值,把x的值代入y=﹣x+10即可求得P的坐标.
【解答过程】解(1)∵A(8,0),
∴OA=8,
SOA |yP|8×(﹣x+10)=﹣4x+40,(0<x<10).
(2)当S=10时,则﹣4x+40=10,解得x,
当x时,y10,
∴当△OPA的面积为10时,点P的坐标为(,).
【题型6 一次函数图象与几何变换】
【例6】已知一次函数y=kx+b的图象过点A(﹣4,﹣2)和点B(2,4)
(1)求直线AB的解析式;
(2)将直线AB平移,使其经过原点O,则线段AB扫过的面积为 12 .
【解题思路】(1)将A、B两点的坐标代入y=kx+b,利用待定系数法即可求出直线AB的解析式;
(2)先利用平移规律求出直线AB平移后的解析式,进而求出线段AB扫过的面积.
【解答过程】解:(1)∵一次函数y=kx+b的图象过点A(﹣4,﹣2)和点B(2,4),
∴,解得,
∴直线AB的解析式为y=x+2;
(2)设直线AB平移后的解析式为y=x+n,
将原点(0,0)代入,得n=0,
∴直线AB平移后的解析式为y=x,
∴将直线AB向下平移2个单位得到直线A′B′,
如图,则A′(﹣4,﹣4),B′(2,2),
∴平行四边形AA′B′B的面积=2×(4+2)=12.
即线段AB扫过的面积为12.
故答案为12.
【变式6-1】若直线y=kx+3与直线y=2x+b关于直线x=1对称,则k、b值分别为( )
A.k=2、b=﹣3 B.k=﹣2、b=﹣3 C.k=﹣2、b=1 D.k=﹣2、b=﹣1
【解题思路】先求出一次函数y=kx+3与y轴交点关于直线x=1的对称点,得到b的值,再求出一次函数y=2x+b与y轴交点关于直线x=1的对称点,代入一次函数y=kx+3,求出k的值即可.
【解答过程】解:∵一次函数y=kx+3与y轴交点为(0,3),
∴点(0,3)关于直线x=1的对称点为(2,3),
代入直线y=2x+b,可得
4+b=3,
解得b=﹣1,
一次函数y=2x﹣1与y轴交点为(0,﹣1),
(0,﹣1)关于直线x=1的对称点为(2,﹣1),
代入直线y=kx+3,可得
2k+3=﹣1,
解得k=﹣2.
故选:D.
【变式6-2】(2018春 沙坪坝区校级期末)如图:一次函数yx+2交y轴于A,交y=3x﹣6于B,y=3x﹣6交x轴于C,直线BC顺时针旋转45°得到直线CD.
(1)求点B的坐标;
(2)求四边形ABCO的面积;
(3)求直线CD的解析式.
【解题思路】(1)构建方程组即可解决问题;
(2)求出A、C两点坐标,根据S四边形ABCO=S△OCB+S△AOB计算即可;
(3)如图,将线段BC绕点B逆时针旋转90得到C′.由题意可知点C′在直线CD上,求出点C′坐标,利用待定系数法即可解决问题;
【解答过程】解:(1)由,解得,
∴B(3,3).
(2)由题意A(0,2),C(2,0),
∴S四边形ABCO=S△OCB+S△AOB2×32×3=6.
(3)如图,将线段BC绕点B逆时针旋转90得到C′.
∵△BCC′是等腰直角三角形,∠BCD=45°,
∴点C′在直线CD上,
由(2)可知,C(2,0).
∵B(3,3),
由旋转的性质可知,C′(6,2),
设直线CD的解析式为y=kx+b,则有,
解得,
∴直线CD的解析式为yx﹣1.
【变式6-3】(2018 沙坪坝区模拟)如图,正比例函数y=kx(k≠0)的图象过点A(2,﹣3).直线y=x+b沿y轴平行移动,与x轴、y轴分别交于点B、C,与直线OA交于点D.
(1)若点D在线段OA上(含端点),求b的取值范围;
(2)当点A关于直线BC的对称点A'恰好落在y轴上时,求△OBD的面积.
【解题思路】(1)将O点和A点的坐标分别代入y=x+b,即可求得b的值,从而求得b的取值范围;
(2)根据直线y=x+b易求得OB=OC,即可得出∠OCB=45°,根据轴对称的性质易求得∠ACD=45°.即可求得∠ACO=90°,从而求得C的纵坐标为﹣3,得出C的坐标为(0,﹣3),即可求得直线y=x﹣3,然后联立方程求得交点D的坐标,根据三角形面积公式即可求得△OBD的面积.
【解答过程】解:(1)当点D和点O重合时,
将点O(0,0)代入y=x+b中,得b=0,
当点D和点A重合时,
将点A(2,﹣3)代入y=x+b中,得﹣3=2+b,即b=﹣5,
∴b的取值范围是﹣5≤b≤0;
(2)将点A(2,﹣3)代入y=kx中,得﹣3=2k,即k,
∴直线OA的解析式为yx,
在y=x+b中,令y=0,则x=﹣b,
∴B(﹣b,0),即OB=|b|,
∴OB=OC,
又∵∠BOC=90°,
∴∠OCB=∠OBC=45°,
∵点A关于直线BC的对称点A'恰好落在y轴上,
∴CD垂直平分AA′,
∴CA=CA′,
∴∠ACD=∠OCB=45°,
∴∠ACO=90°,
∴OC=|yA|=3,
∴OB=OC=3,即C(0,﹣3),
将点C(0,﹣3)代入y=x+b中,得﹣3=0+b,
∴b=﹣3,
∴直线BC的解析式为y=x﹣3,
由得,
∴D(,),
∴S△OBDOB |yD|3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
