第五章一次函数专题5.4 一次函数与方程、不等式的关系-重难点题型(含解析)
文档属性
| 名称 | 第五章一次函数专题5.4 一次函数与方程、不等式的关系-重难点题型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 16:26:27 | ||
图片预览




文档简介
一次函数与方程、不等式的关系6大题型
【知识点1 一次函数与一元一次方程、不等式的关系】
1. 任何一个一元一次方程都可转化为:kx+b=0(k、b为常数,k≠0)的形式.
而一次函数解析式形式正是y=kx+b(k、b为常数,k≠0).当函数值为0时,即kx+b=0就与一元一次方程完全相同.
结论:由于任何一元一次方程都可转化为kx+b=0(k、b为常数,k≠0)的形式.所以解一元一次方程可以转化为:当一次函数值为0时,求相应的自变量的值.
从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值.
2.解一元一次不等式可以看作:当一次函数的函数值大(小)于0时,求自变量相应的取值范围.
【题型1 一次函数的与一元一次方程】
【例1】(2020秋 包河区期中)根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)关于x的方程kx+b=0的解;
(2)代数式k+b的值;
(3)关于x的方程kx+b=﹣3的解.
【变式1-1】(2021秋 泰兴市校级期末)已知一次函数y=kx+1与yx+b的图象相交于点(2,5),求关于x的方程kx+b=0的解.
【变式1-2】一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=4的解为多少?
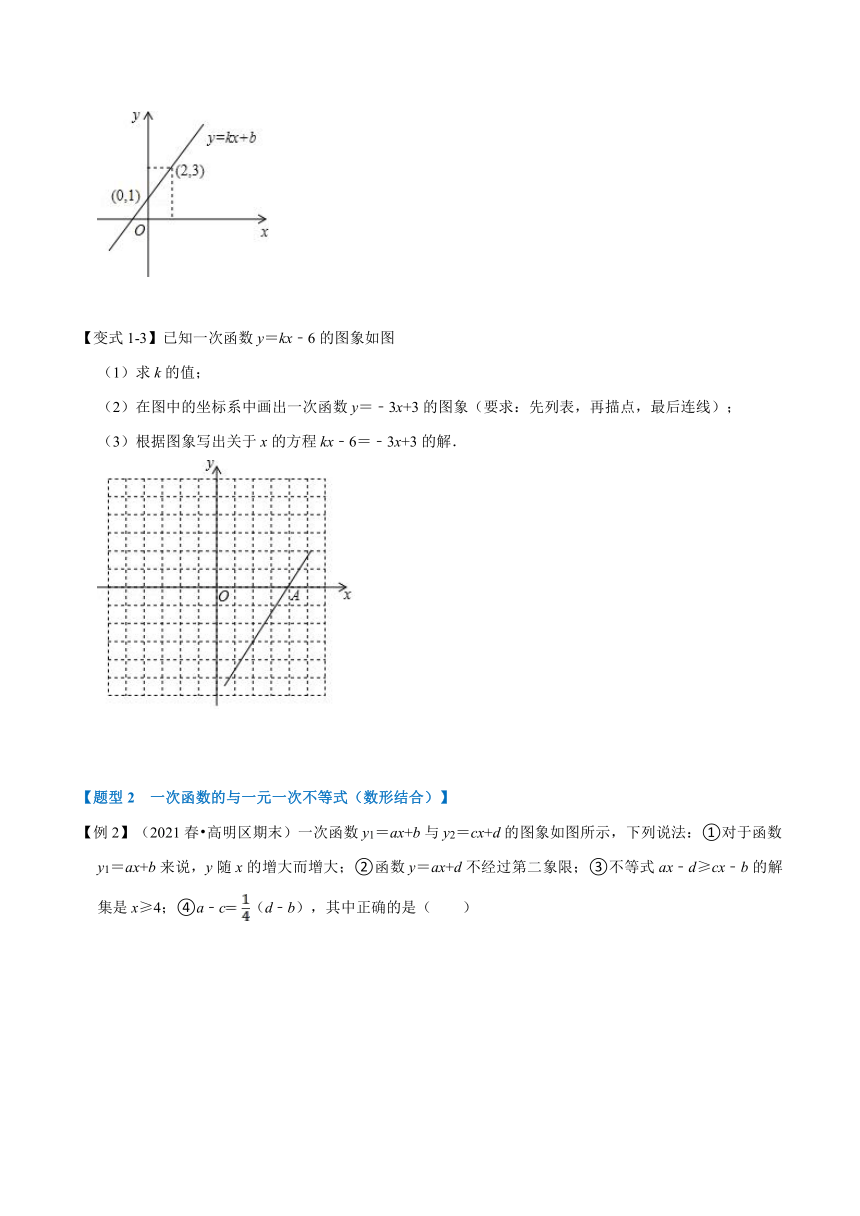
【变式1-3】已知一次函数y=kx﹣6的图象如图
(1)求k的值;
(2)在图中的坐标系中画出一次函数y=﹣3x+3的图象(要求:先列表,再描点,最后连线);
(3)根据图象写出关于x的方程kx﹣6=﹣3x+3的解.
【题型2 一次函数的与一元一次不等式(数形结合)】
【例2】(2021春 高明区期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:①对于函数y1=ax+b来说,y随x的增大而增大;②函数y=ax+d不经过第二象限;③不等式ax﹣d≥cx﹣b的解集是x≥4;④a﹣c(d﹣b),其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
【变式2-1】(2021 安徽模拟)已知一次函数y1=kx+3(k为常数,且k≠0)和y2=x﹣3.当x<2时,y1>y2,则k的取值范围是( )
A.﹣2≤k≤1且k≠0 B.k≤﹣2
C.k≥1 D.﹣2<k<1且k≠0
【变式2-2】(2021春 盐湖区校级期末)我们知道,若ab>0.则有或.如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
A.x>2 B.﹣0.5<x<2
C.0<x<2 D.x<﹣0.5或x>2
【变式2-3】(2021春 中山市期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:
①对于函数y1=ax+b来说,y随x的增大而减小;
②函数y=ax+d的图象不经过第一象限;
③不等式ax+b>cx+d的解集是x>3;
④d﹣b=3(a﹣c).
其中正确的有( )
A.①③ B.②③④ C.①②④ D.②③
【题型3 一次函数的与一元一次不等式(取值范围)】
【例3】(2021春 海淀区期末)在平面直角坐标系xOy中,直线l:y1=x+1与直线l2:y2=2x﹣2交于点A.
(1)求点A的坐标;
(2)当y1>y2时,直接写出x的取值范围;
(3)已知直线l3:y3=kx+1,当x<3时,对于x的每一个值,都有y3>y2,直接写出k的取值范围.
【变式3-1】(2021春 茌平区期末)已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
【变式3-2】(2021春 海珠区期末)已知一次函数y1=ax+b的图象交x轴和y轴于点B和D;另一个一次函数y2=bx+a的图象交x轴和y轴于点C和E,且两个函数的图象交于点A(1,4)
(1)当a,b为何值时,y1和y2的图象重合;
(2)当0<a<4,且在x<1时,则y1>y2成立.求b的取值范围;
【变式3-3】(2020春 赣县区期末)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(﹣2,4),且与正比例函数yx的图象交于点B(a,2).
(1)求a的值及一次函数y=kx+b的解析式;
(2)若一次函数y=kx+b的图象与x轴交于点C,且正比例函数yx的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
(3)直接写出关于x的不等式0x<kx+b的解集.
【题型4 一次函数与一元一次不等式(面积问题)】
【例4】(2021春 诸城市期末)如图,直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3);直线y=1﹣mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1﹣mx的解集是x.
(1)分别求出k,b,m的值;
(2)求S△ACD.
【变式4-1】(2021春 东辽县期末)已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x﹣4与x轴于D,与直线AB相交于点C.
(1)求点C的坐标;
(2)根据图象,写出关于x的不等式2x﹣4>kx+5的解集;
(3)求△ADC的面积.
【变式4-2】(2020春 宁化县校级月考)如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P(a,2).
(1)求出不等式2x≤kx+3的解集;
(2)求出△OAP的面积.
【变式4-3】已知一次函数y1=﹣2x﹣3与y2x+2.
(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3x+2的解集为 ;
(3)求两图象和y轴围成的三角形的面积.
【题型5 一次函数的与一元一次不等式(求点的坐标)】
【例5】如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4),且MN=5.
(1)求直线MN的解析式;
(2)根据图象,写出不等式kx+b≥0的解集;
(3)若点P在x轴上,且点P到直线y=kx+b的距离为,直接写出符合条件的点P的坐标.
【变式5-1】(2021春 顺德区期末)一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)由图可知,不等式kx+b>0的解集是 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1.
①求点B的坐标;
②求a的值.
【变式5-2】(2020秋 南京期末)已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的函数关系式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,直接写出当x在什么范围内,不等式2x﹣4>kx+b.
【变式5-3】在平面直角坐标系中,直线y=﹣2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=﹣2x+1交于点B,设点B的横坐标为﹣2.
(1)求点B的坐标及k的值;
(2)求直线y=﹣2x+1、直线y=x+k与y轴所围成的△ABC的面积;
(3)根据图象直接写出不等式﹣2x+1>x+k的解集.
【知识点2 一次函数与二元一次方程】
(1)每个二元一次方程都对应一个一次函数,也对应一条直线.
(2)解二元一次方程组,从“数”的角度看,相当于考虑当自変量为何值时两个函数的值相等,以及这个函数值是多少,从“形”的角度看,相当于确定两条直线的交点坐标.
【题型6 一次函数与二元一次方程】
【例6】(2021 济南二模)中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式所对应两直线交点坐标是 .
【变式6-1】如图,直线y=﹣2x+6与直线y=mx+n相交于点M(p,4).
(1)求p的值;
(2)直接写出关于x,y的二元一次方程组的解;
(3)判断直线y=3nx+m﹣2n是否也过点M?并说明理由.
【变式6-2】(2021秋 文成县期末)如图,l1,l2分别表示两个一次函数的图象,它们相交于点P,
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解;
(3)求出图中△APB的面积.
【变式6-3】(2020秋 西安期末)学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)当参加老师的人数为多少人时,选择甲旅行社合算?
(3)如果全共有50人参加时,选择哪家旅行社合算?
一次函数与方程、不等式的关系-重难点题型
【知识点1 一次函数与一元一次方程、不等式的关系】
1. 任何一个一元一次方程都可转化为:kx+b=0(k、b为常数,k≠0)的形式.
而一次函数解析式形式正是y=kx+b(k、b为常数,k≠0).当函数值为0时,即kx+b=0就与一元一次方程完全相同.
结论:由于任何一元一次方程都可转化为kx+b=0(k、b为常数,k≠0)的形式.所以解一元一次方程可以转化为:当一次函数值为0时,求相应的自变量的值.
从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值.
2.解一元一次不等式可以看作:当一次函数的函数值大(小)于0时,求自变量相应的取值范围.
【题型1 一次函数的与一元一次方程】
【例1】(2020秋 包河区期中)根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)关于x的方程kx+b=0的解;
(2)代数式k+b的值;
(3)关于x的方程kx+b=﹣3的解.
【解题思路】(1)利用函数图象写出函数值为0时对应的自变量的值即可;
(2)利用函数图象写出x=1时对应的函数值即可
(3)利用函数图象写出函数值为﹣3时对应的自变量的值即可.
【解答过程】解:(1)当x=2时,y=0,
所以方程kx+b=0的解为x=2;
(2)当x=1时,y=﹣1,
所以代数式k+b的值为﹣1;
(3)当x=﹣1时,y=﹣3,
所以方程kx+b=﹣3的解为x=﹣1.
【变式1-1】(2021秋 泰兴市校级期末)已知一次函数y=kx+1与yx+b的图象相交于点(2,5),求关于x的方程kx+b=0的解.
【解题思路】首先将(2,5)点代入一次函数解析式求出k,b的值,进而解方程得出答案.
【解答过程】解:∵一次函数y=kx+1与yx+b的图象相交于点(2,5),
∴5=2k+1,52+b,
解得:k=2,b=6,
则kx+b=0为:2x+6=0,
解得:x=﹣3.
【变式1-2】一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=4的解为多少?
【解题思路】先求出函数的解析式,再把y=4代入,即可求出x.
【解答过程】解:把(0,1)和(2,3)代入y=kx+b得:
,
解得:k=1,b=1,
即y=x+1,
当y=4时,x+1=4,
解得:x=3,
∴方程kx+b=4的解为x=3.
【变式1-3】已知一次函数y=kx﹣6的图象如图
(1)求k的值;
(2)在图中的坐标系中画出一次函数y=﹣3x+3的图象(要求:先列表,再描点,最后连线);
(3)根据图象写出关于x的方程kx﹣6=﹣3x+3的解.
【解题思路】(1)将点(4,0)代入y=kx﹣6,利用待定系数求出k的值;
(2)利用描点法画出一次函数y=﹣3x+3的图象;
(3)根据图象写出它们的交点坐标,即可得到关于x的方程kx﹣6=﹣3x+3的解.
【解答过程】解:(1)∵一次函数y=kx﹣6的图象过点(4,0),
∴4k﹣6=0,
∴k;
(2)列表:
描点:在平面直角坐标系中描出两点(0,3)、(1,0),
连线:过点(0,3)、(1,0)画直线,得出一次函数y=﹣3x+3的图象;
(3)一次函数y=kx﹣6与y=﹣3x+3的图象交于点(2,﹣3),
则关于x的方程kx﹣6=﹣3x+3的解为x=2.
【题型2 一次函数的与一元一次不等式(数形结合)】
【例2】(2021春 高明区期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:①对于函数y1=ax+b来说,y随x的增大而增大;②函数y=ax+d不经过第二象限;③不等式ax﹣d≥cx﹣b的解集是x≥4;④a﹣c(d﹣b),其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
【解题思路】根据题意和函数图象中的数据,可以判断各个小题中的结论是否成立,从而可以解答本题.
【解答过程】解:由图象可得,
对于函数y=ax+b来说,y随x的增大而增大,故①正确;
a>0,d>0,则函数y=ax+d经过第一、二、三象限,不经过第四象限,故②不正确;
由ax﹣d≥cx﹣b可得ax+b≥cx+d,故不等式ax﹣d≥cx﹣b的解集是x≥4,故③正确;
4a+b=4c+d可以得到a﹣c(d﹣b),故④正确;
故选:B.
【变式2-1】(2021 安徽模拟)已知一次函数y1=kx+3(k为常数,且k≠0)和y2=x﹣3.当x<2时,y1>y2,则k的取值范围是( )
A.﹣2≤k≤1且k≠0 B.k≤﹣2
C.k≥1 D.﹣2<k<1且k≠0
【解题思路】解不等式kx+3>x﹣3,根据题意得出k﹣1<0且2且k≠0,解此不等式即可.
【解答过程】解:∵一次函数y1=kx+3(k为常数,且k≠0)和y2=x﹣3,当x<2时,y1>y2,
∴kx+3>x﹣3,
∴kx﹣x>﹣6,
∴k﹣1<0且2且k≠0,
当k﹣1<0时,2时,k≥﹣2,
所以不等式组的解集为﹣2≤k<1且k≠0;
当k=1时,也成立,
故k的取值范围是﹣2≤k≤1且k≠0,
故选:A.
【变式2-2】(2021春 盐湖区校级期末)我们知道,若ab>0.则有或.如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
A.x>2 B.﹣0.5<x<2
C.0<x<2 D.x<﹣0.5或x>2
【解题思路】由若不等式(kx+b)(mx+n)>0,则或,然后分类讨论,分别根据函数图象求得解集.
【解答过程】解:∵若ab>0.则有或,
∴若不等式(kx+b)(mx+n)>0,则或.
当,由图得:,此时该不等式无解.
当,由图得:,此时不等式组的解集为﹣0.5<x<2.
综上:﹣0.5<x<2.
故选:B.
【变式2-3】(2021春 中山市期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:
①对于函数y1=ax+b来说,y随x的增大而减小;
②函数y=ax+d的图象不经过第一象限;
③不等式ax+b>cx+d的解集是x>3;
④d﹣b=3(a﹣c).
其中正确的有( )
A.①③ B.②③④ C.①②④ D.②③
【解题思路】仔细观察图象:①根据函数图象直接得到结论;
②观察函数图象可以直接得到答案;
③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;
④根据两直线交点可以得到答案.
【解答过程】解:由图象可得:对于函数y1=ax+b来说,y随x的增大而减小,故①说法正确;
由于a<0,d<0,所以函数y2=ax+d的图象经过第二,三,四象限,即不经过第一象限,故②说法正确,
由图象可得当x<3时,一次函数y1=ax+b图象在y2=cx+d的图象上方,
∴ax+b>cx+d的解集是x<3,故③说法不正确;
∵一次函数y1=ax+b与y2=cx+d的图象的交点的横坐标为3,
∴3a+b=3c+d
∴3a﹣3c=d﹣b,
∴d﹣b=3(a﹣c).故④说法正确,
故选:C.
【题型3 一次函数的与一元一次不等式(取值范围)】
【例3】(2021春 海淀区期末)在平面直角坐标系xOy中,直线l:y1=x+1与直线l2:y2=2x﹣2交于点A.
(1)求点A的坐标;
(2)当y1>y2时,直接写出x的取值范围;
(3)已知直线l3:y3=kx+1,当x<3时,对于x的每一个值,都有y3>y2,直接写出k的取值范围.
【解题思路】(1)由直线l:y1=x+1与直线l2:y2=2x﹣2交于点A,故可联立方程组:得,故A(3,4).
(2)根据函数图象,可知:当y1>y2时,x<3.
(3)当x<3时,对于x的每一个值,都有y3>y2,故当x<3,y3﹣y2>0恒成立,得1≤k≤2.
【解答过程】解:(1)由题意得:
解得:
∴A(3,4).
(2)如图,当y1>y2时,x<3.
(3)当x<3,y3>y2恒成立,则x<3,y3﹣y2>0恒成立.
∵y3=kx+1,y2=2x﹣2,
∴y3﹣y2=(kx+1)﹣(2x﹣2)=(k﹣2)x+3.
∴若x<3,y3﹣y2>0恒成立,则[(k﹣2)x+3]min>0.
当k﹣2=0,即k=2,[(k﹣2)x+3]min=3>0.
当k﹣2>0,即k>2,[(k﹣2)x+3]min不存在.
当k﹣2<0,即k<2,[(k﹣2)x+3]min=3(k﹣2)+3≥0,故k≥1.
综上:1≤k≤2.
【变式3-1】(2021春 茌平区期末)已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
【解题思路】(1)将两个函数的解析式联立得到方程组,解此方程组即可求出点A的坐标;
(2)先根据函数解析式求得B、C两点的坐标,可得BC的长,再利用三角形的面积公式可得结果;
(3)根据函数图象以及点A坐标即可求解.
【解答过程】解:(1)解方程组,得,
所以点A坐标为(1,﹣3);
(2)当y1=0时,﹣x﹣2=0,x=﹣2,则B点坐标为(﹣2,0);
当y2=0时,x﹣4=0,x=4,则C点坐标为(4,0);
∴BC=4﹣(﹣2)=6,
∴△ABC的面积6×3=9;
【变式3-2】(2021春 海珠区期末)已知一次函数y1=ax+b的图象交x轴和y轴于点B和D;另一个一次函数y2=bx+a的图象交x轴和y轴于点C和E,且两个函数的图象交于点A(1,4)
(1)当a,b为何值时,y1和y2的图象重合;
(2)当0<a<4,且在x<1时,则y1>y2成立.求b的取值范围;
【解题思路】(1)把A(1,4)代入y1=ax+b求得a+b=4,得到b=4﹣a,于是得到结论;
(2)根据题意列不等式即可得到结论;
【解答过程】解:(1)∵y1=ax+b的图象过点A(1,4),
∴a+b=4,
∴b=4﹣a,
∴y1=ax+(4﹣a),y2=(4﹣a)x+a,
∵y1和y2的图象重合,
∴a=4﹣a,
∴a=2,b=2;
即当a=2,b=2时,y1和y2的图象重合;
(2)∵a+b=4,如图1,
∴a=4﹣b,
∴y1=(4﹣b)x+b,
y2=bx+(4﹣b),
∵0<a<4,0<4﹣b<4且x<1时,y1>y2成立,
∴由图象得4﹣b<b,
∴2<b<4;
【变式3-3】(2020春 赣县区期末)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(﹣2,4),且与正比例函数yx的图象交于点B(a,2).
(1)求a的值及一次函数y=kx+b的解析式;
(2)若一次函数y=kx+b的图象与x轴交于点C,且正比例函数yx的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
(3)直接写出关于x的不等式0x<kx+b的解集.
【解题思路】(1)先确定B的坐标,然后根据待定系数法求解析式;
(2)先求得C的坐标,然后根据题意求得平移后的直线的解析式,把C的坐标代入平移后的直线的解析式,即可求得M的值;
(3)找出直线yx落在y=kx+b的下方且在x轴上方的部分对应的x的取值范围即可.
【解答过程】解:(1)∵正比例函数yx的图象经过点B(a,2),
∴2a,解得,a=﹣3,
∴B(﹣3,2),
∵一次函数y=kx+b的图象经过点A(﹣2,4),B(﹣3,2),
∴,解得,
∴一次函数y=kx+b的解析式为y=2x+8;
(2)∵一次函数y=2x+8的图象与x轴交于点C,
∴C(﹣4,0),
∵正比例函数yx的图象向下平移m(m>0)个单位长度后经过点C,
∴平移后的函数的解析式为yx﹣m,
∴0(﹣4)﹣m,解得m;
(3)∵一次函y=kx+b与正比例函数yx的图象交于点B(﹣3,2),
且一次函数y=2x+8的图象与x轴交于点C(﹣4,0),
∴关于x的不等式0x<kx+b的解集是﹣3<x<0.
【题型4 一次函数与一元一次不等式(面积问题)】
【例4】(2021春 诸城市期末)如图,直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3);直线y=1﹣mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1﹣mx的解集是x.
(1)分别求出k,b,m的值;
(2)求S△ACD.
【解题思路】(1)首先利用待定系数法确定直线的解析式,然后根据关于x的不等式kx+b>1﹣mx的解集是x得到点D的横坐标为,再将x代入yx+3,得:y,将x,y代入y=1﹣mx求得m=1即可;
(2)先确定直线与x轴的交点坐标,然后利用三角形的面积公式计算即可.
【解答过程】解:(1)∵直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3),
,
解得:k,b=3,
∵关于x的不等式kx+b>1﹣mx的解集是x,
∴点D的横坐标为,
将x代入yx+3,得:y,
∴D(,),
将x,y代入y=1﹣mx,
解得:m=1;
(2)如图,过点D作DH⊥AC于H,则DH
对于y=1﹣x,令y=0,得:x=1,
∴点C的坐标为(1,0),
∴S△ACD AC DH[1﹣(﹣2)].
【变式4-1】(2021春 东辽县期末)已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x﹣4与x轴于D,与直线AB相交于点C.
(1)求点C的坐标;
(2)根据图象,写出关于x的不等式2x﹣4>kx+5的解集;
(3)求△ADC的面积.
【解题思路】(1)根据点A的坐标利用待定系数法可求出直线AB的解析式,联立直线AB、CD的解析式成方程组,通过解方程组即可求出点C的坐标;
(2)根据直线AB、CD的上下位置关系结合点C的坐标,即可得出不等式2x﹣4>kx+5的解集;
(3)利用一次函数图象上点的坐标特征可求出点D的坐标,再根据三角形的面积公式即可求出△ADC的面积.
【解答过程】解:(1)∵直线y=kx+5经过点A(5,0),
∴5k+5=0,
解得:k=﹣1,
∴直线AB的解析式为y=﹣x+5.
联立直线AB、CD的解析式成方程组,
,解得:,
∴点C的坐标为(3,2).
(2)观察函数图象可知:当x>3时,直线y=2x﹣4在直线y=﹣x+5的上方,
∴不等式2x﹣4>kx+5的解集为x>3.
(3)当y=2x﹣4=0时,x=2,
∴点D的坐标为(2,0),
∴S△ACD(xA﹣xD) yC(5﹣2)×2=3.
【变式4-2】(2020春 宁化县校级月考)如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P(a,2).
(1)求出不等式2x≤kx+3的解集;
(2)求出△OAP的面积.
【解题思路】(1)利用一次函数图象上点的坐标特征先求出a的值,然后观察函数图象,写出直线y=kx+3在直线y=2x上方所对应的自变量的取值范围即可;
(2)先求出直线l2的解析式,再求出A点坐标,然后利用三角形面积公式求解.
【解答过程】解:(1)把P(a,2)代入y=2x得2a=2,解得a=1,则P(1,2),
当x≤1时,2x≤kx+3,
所以不等式2x≤kx+3的解集为x≤1;
(2)把P(1,2)代入y=kx+3得k+3=2,解得k=﹣1,
所以直线l2的解析式为y=﹣x+3,当y=0时,﹣x+3=0,解得x=3,则A(3,0),
所以△OAP的面积2×3=3.
【变式4-3】已知一次函数y1=﹣2x﹣3与y2x+2.
(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3x+2的解集为 x<﹣2 ;
(3)求两图象和y轴围成的三角形的面积.
【解题思路】(1)先求出直线y1=﹣2x﹣3,y2x+2与x轴和y轴的交点,再画出两函数图象即可;
(2)直线y1=﹣2x﹣3的图象落在直线y2x+2上方的部分对应的x的取值范围就是不等式﹣2x﹣3x+2的解集;
(3)根据三角形的面积公式求解即可.
【解答过程】解:(1)函数y1=﹣2x﹣3与x轴和y轴的交点分别是(﹣1.5,0)和(0,﹣3),
y2x+2与x轴和y轴的交点分别是(﹣4,0)和(0,2),
其图象如图:
(2)观察图象可知,函数y1=﹣2x﹣3与y2x+2交于点(﹣2,1),
当x<﹣2时,直线y1=﹣2x﹣3的图象落在直线y2x+2的上方,即﹣2x﹣3x+2,
所以不等式﹣2x﹣3x+2的解集为x<﹣2;
故答案为x<﹣2;
(3)∵y1=﹣2x﹣3与y2x+2与y轴分别交于点A(0,﹣3),B(0,2),
∴AB=5,
∵y1=﹣2x﹣3与y2x+2交于点C(﹣2,1),
∴△ABC的边AB上的高为2,
∴S△ABC5×2=5.
【题型5 一次函数的与一元一次不等式(求点的坐标)】
【例5】如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4),且MN=5.
(1)求直线MN的解析式;
(2)根据图象,写出不等式kx+b≥0的解集;
(3)若点P在x轴上,且点P到直线y=kx+b的距离为,直接写出符合条件的点P的坐标.
【解题思路】(1)把点M、N的坐标分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值;
(2)直线y=kx+b在x轴及其上方的部分对应的x的取值范围即为所求;
(3)作△OMN的高OA.根据三角形的面积公式求出OA,则点P的坐标是(0,0);在x轴上作O关于M的对称点为(6,0),易得(6,0)到直线y=kx+b的距离也为.
【解答过程】解:(1)∵直线y=kx+b与坐标轴相交于点M(3,0),N(0,4),
所以,
解得:,
∴直线MN的解析式为:yx+4;
(2)根据图形可知,当x≤3时,y=kx+b在x轴及其上方,即kx+b≥0,
则不等式kx+b≥0的解集为x≤3;
(3)如图,作△OMN的高OA.
∵S△OMNMN OAOM ON,
∴OA,
∴点P的坐标是(0,0);
在x轴上作O关于M的对称点为(6,0),易得(6,0)到直线y=kx+b的距离也为,
所以点P的坐标是(0,0)或(6,0).
【变式5-1】(2021春 顺德区期末)一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)由图可知,不等式kx+b>0的解集是 x>﹣2 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1.
①求点B的坐标;
②求a的值.
【解题思路】(1)根据函数图象和题意可以直接写出不等式kx+b>0的解集;
(2)①由题意可以求得k、b的值,然后将x=1代入y1=kx+b即可求得点B的坐标;
②根据点B也在函数y2=﹣4x+a的图象上,从而可以求得a的值.
【解答过程】解:(1)∵A(0,4),C(﹣2,0)在一次函数y1=kx+b上,
∴不等式kx+b>0的解集是x>﹣2,
故答案为:x>﹣2;
(2)①∵A(0,4),C(﹣2,0)在一次函数y1=kx+b上,
∴,得,
∴一次函数y1=2x+4,
∵不等式kx+b>﹣4x+a的解集是x>1,
∴点B的横坐标是x=1,
当x=1时,y1=2×1+4=6,
∴点B的坐标为(1,6);
②∵点B(1,6),
∴6=﹣4×1+a,得a=10,
即a的值是10.
【变式5-2】(2020秋 南京期末)已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的函数关系式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,直接写出当x在什么范围内,不等式2x﹣4>kx+b.
【解题思路】(1)利用待定系数法即可求得函数的解析式;
(2)解两个函数解析式组成方程组即可求解;
(3)关于x的不等2x﹣4>kx+b的解集就是函数y=kx+b的图象在下边的部分自变量的取值范围.
【解答过程】解:(1)根据题意得,
解得,
则直线AB的解析式是y=﹣x+5;
(2)根据题意得,
解得:,
则C的坐标是(3,2);
(3)根据图象可得不等式的解集是x>3.
【变式5-3】在平面直角坐标系中,直线y=﹣2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=﹣2x+1交于点B,设点B的横坐标为﹣2.
(1)求点B的坐标及k的值;
(2)求直线y=﹣2x+1、直线y=x+k与y轴所围成的△ABC的面积;
(3)根据图象直接写出不等式﹣2x+1>x+k的解集.
【解题思路】(1)对于y=﹣2x+1,计算自变量为﹣2时的函数值可得到B点坐标,然后把B点坐标代入y=x+k可得到k的值;
(2)先确定两直线与y轴的交点A、C的坐标,然后利用三角形面积公式求解;
(3)观察函数图象,写出直线y=﹣2x+1在直线y=x+k上方所对应的自变量的范围即可.
【解答过程】解:(1)当x=﹣2时,y=﹣2×(﹣2)+1=5,则B(﹣2,5).
把B(﹣2,5)代入y=x+k得﹣2+k=5,解得k=7;
(2)当x=0时,y=﹣2x+1=1,则C(0,1);
当x=0时,y=x+7=7,则A(0,7)
所以AC=7﹣1=6,
所以S△ABC6×2=6;
(3)x<﹣2.
【知识点2 一次函数与二元一次方程】
(1)每个二元一次方程都对应一个一次函数,也对应一条直线.
(2)解二元一次方程组,从“数”的角度看,相当于考虑当自変量为何值时两个函数的值相等,以及这个函数值是多少,从“形”的角度看,相当于确定两条直线的交点坐标.
【题型6 一次函数与二元一次方程】
【例6】(2021 济南二模)中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式所对应两直线交点坐标是 (2,5) .
【解题思路】根据题意得出方程组,求出方程组的解,再得出答案即可.
【解答过程】解:根据题意得:
,
①+②,得x=2,
把x=2代入①,得8﹣y=3,
解得:y=5,
所以方程组的解为,
∴两直线交点坐标是(2,5),
故答案为:(2,5).
【变式6-1】如图,直线y=﹣2x+6与直线y=mx+n相交于点M(p,4).
(1)求p的值;
(2)直接写出关于x,y的二元一次方程组的解;
(3)判断直线y=3nx+m﹣2n是否也过点M?并说明理由.
【解题思路】(1)根据直线y=﹣2x+6经过点M,即可求出p.
(2)由图象可知交点的坐标就是方程组的解.
(3)先求出m+n=4,用代入法可以解决.
【解答过程】解:(1)∵直线y=﹣2x+6经过点M(p,4),
∴4=﹣2p+6,
∴p=1.
(2)由图象可知方程组的解为,
(3)结论:直线y=3nx+m﹣2n经过点M,理由如下:
∵点M(1,4)在直线y=mx+n上,
∴m+n=4,
∴当x=1,时,y=3nx+m﹣2n=m+n=4,
∴直线y=3nx+m﹣2n经过点M.
【变式6-2】(2021秋 文成县期末)如图,l1,l2分别表示两个一次函数的图象,它们相交于点P,
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解;
(3)求出图中△APB的面积.
【解题思路】(1)由图可得两函数与坐标轴的交点坐标,用待定系数法可求出它们的函数解析式;
(2)联立两个一次函数的解析式,所得方程组的解即为P点坐标.
(3)△ABP中,以AB为底,P点横坐标的绝对值为高,可求出△ABP的面积.
【解答过程】解:(1)设直线l1的解析式是y=kx+b,已知l1经过点(0,3),(1,0),
可得:,解得,
则函数的解析式是y=﹣3x+3;
同理可得l2的解析式是:y=x﹣2.
(2)点P的坐标可看作是二元一次方程组的解.
(3)易知:A(0,3),B(0,﹣2),P(,);
∴S△APBAB |xP|5.
【变式6-3】(2020秋 西安期末)学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)当参加老师的人数为多少人时,选择甲旅行社合算?
(3)如果全共有50人参加时,选择哪家旅行社合算?
【解题思路】(1)当两函数图象相交时,两家旅行社收费相同,由图象即可得出答案.
(2)由图象比较收费y1、y2,即可得出答案.
(3)当有50人时,比较收费y1、y2,即可得出答案.
【解答过程】解:(1)当两函数图象相交时,两家旅行社收费相同,由图象知为30人;
(2)由图象知:当有30人以下时,y1<y2,所以选择甲旅行社合算;
(3)由图象知:当有50人参加时,y1>y2,所以选择乙旅行社合算;
【知识点1 一次函数与一元一次方程、不等式的关系】
1. 任何一个一元一次方程都可转化为:kx+b=0(k、b为常数,k≠0)的形式.
而一次函数解析式形式正是y=kx+b(k、b为常数,k≠0).当函数值为0时,即kx+b=0就与一元一次方程完全相同.
结论:由于任何一元一次方程都可转化为kx+b=0(k、b为常数,k≠0)的形式.所以解一元一次方程可以转化为:当一次函数值为0时,求相应的自变量的值.
从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值.
2.解一元一次不等式可以看作:当一次函数的函数值大(小)于0时,求自变量相应的取值范围.
【题型1 一次函数的与一元一次方程】
【例1】(2020秋 包河区期中)根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)关于x的方程kx+b=0的解;
(2)代数式k+b的值;
(3)关于x的方程kx+b=﹣3的解.
【变式1-1】(2021秋 泰兴市校级期末)已知一次函数y=kx+1与yx+b的图象相交于点(2,5),求关于x的方程kx+b=0的解.
【变式1-2】一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=4的解为多少?
【变式1-3】已知一次函数y=kx﹣6的图象如图
(1)求k的值;
(2)在图中的坐标系中画出一次函数y=﹣3x+3的图象(要求:先列表,再描点,最后连线);
(3)根据图象写出关于x的方程kx﹣6=﹣3x+3的解.
【题型2 一次函数的与一元一次不等式(数形结合)】
【例2】(2021春 高明区期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:①对于函数y1=ax+b来说,y随x的增大而增大;②函数y=ax+d不经过第二象限;③不等式ax﹣d≥cx﹣b的解集是x≥4;④a﹣c(d﹣b),其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
【变式2-1】(2021 安徽模拟)已知一次函数y1=kx+3(k为常数,且k≠0)和y2=x﹣3.当x<2时,y1>y2,则k的取值范围是( )
A.﹣2≤k≤1且k≠0 B.k≤﹣2
C.k≥1 D.﹣2<k<1且k≠0
【变式2-2】(2021春 盐湖区校级期末)我们知道,若ab>0.则有或.如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
A.x>2 B.﹣0.5<x<2
C.0<x<2 D.x<﹣0.5或x>2
【变式2-3】(2021春 中山市期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:
①对于函数y1=ax+b来说,y随x的增大而减小;
②函数y=ax+d的图象不经过第一象限;
③不等式ax+b>cx+d的解集是x>3;
④d﹣b=3(a﹣c).
其中正确的有( )
A.①③ B.②③④ C.①②④ D.②③
【题型3 一次函数的与一元一次不等式(取值范围)】
【例3】(2021春 海淀区期末)在平面直角坐标系xOy中,直线l:y1=x+1与直线l2:y2=2x﹣2交于点A.
(1)求点A的坐标;
(2)当y1>y2时,直接写出x的取值范围;
(3)已知直线l3:y3=kx+1,当x<3时,对于x的每一个值,都有y3>y2,直接写出k的取值范围.
【变式3-1】(2021春 茌平区期末)已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
【变式3-2】(2021春 海珠区期末)已知一次函数y1=ax+b的图象交x轴和y轴于点B和D;另一个一次函数y2=bx+a的图象交x轴和y轴于点C和E,且两个函数的图象交于点A(1,4)
(1)当a,b为何值时,y1和y2的图象重合;
(2)当0<a<4,且在x<1时,则y1>y2成立.求b的取值范围;
【变式3-3】(2020春 赣县区期末)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(﹣2,4),且与正比例函数yx的图象交于点B(a,2).
(1)求a的值及一次函数y=kx+b的解析式;
(2)若一次函数y=kx+b的图象与x轴交于点C,且正比例函数yx的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
(3)直接写出关于x的不等式0x<kx+b的解集.
【题型4 一次函数与一元一次不等式(面积问题)】
【例4】(2021春 诸城市期末)如图,直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3);直线y=1﹣mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1﹣mx的解集是x.
(1)分别求出k,b,m的值;
(2)求S△ACD.
【变式4-1】(2021春 东辽县期末)已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x﹣4与x轴于D,与直线AB相交于点C.
(1)求点C的坐标;
(2)根据图象,写出关于x的不等式2x﹣4>kx+5的解集;
(3)求△ADC的面积.
【变式4-2】(2020春 宁化县校级月考)如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P(a,2).
(1)求出不等式2x≤kx+3的解集;
(2)求出△OAP的面积.
【变式4-3】已知一次函数y1=﹣2x﹣3与y2x+2.
(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3x+2的解集为 ;
(3)求两图象和y轴围成的三角形的面积.
【题型5 一次函数的与一元一次不等式(求点的坐标)】
【例5】如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4),且MN=5.
(1)求直线MN的解析式;
(2)根据图象,写出不等式kx+b≥0的解集;
(3)若点P在x轴上,且点P到直线y=kx+b的距离为,直接写出符合条件的点P的坐标.
【变式5-1】(2021春 顺德区期末)一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)由图可知,不等式kx+b>0的解集是 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1.
①求点B的坐标;
②求a的值.
【变式5-2】(2020秋 南京期末)已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的函数关系式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,直接写出当x在什么范围内,不等式2x﹣4>kx+b.
【变式5-3】在平面直角坐标系中,直线y=﹣2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=﹣2x+1交于点B,设点B的横坐标为﹣2.
(1)求点B的坐标及k的值;
(2)求直线y=﹣2x+1、直线y=x+k与y轴所围成的△ABC的面积;
(3)根据图象直接写出不等式﹣2x+1>x+k的解集.
【知识点2 一次函数与二元一次方程】
(1)每个二元一次方程都对应一个一次函数,也对应一条直线.
(2)解二元一次方程组,从“数”的角度看,相当于考虑当自変量为何值时两个函数的值相等,以及这个函数值是多少,从“形”的角度看,相当于确定两条直线的交点坐标.
【题型6 一次函数与二元一次方程】
【例6】(2021 济南二模)中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式所对应两直线交点坐标是 .
【变式6-1】如图,直线y=﹣2x+6与直线y=mx+n相交于点M(p,4).
(1)求p的值;
(2)直接写出关于x,y的二元一次方程组的解;
(3)判断直线y=3nx+m﹣2n是否也过点M?并说明理由.
【变式6-2】(2021秋 文成县期末)如图,l1,l2分别表示两个一次函数的图象,它们相交于点P,
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解;
(3)求出图中△APB的面积.
【变式6-3】(2020秋 西安期末)学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)当参加老师的人数为多少人时,选择甲旅行社合算?
(3)如果全共有50人参加时,选择哪家旅行社合算?
一次函数与方程、不等式的关系-重难点题型
【知识点1 一次函数与一元一次方程、不等式的关系】
1. 任何一个一元一次方程都可转化为:kx+b=0(k、b为常数,k≠0)的形式.
而一次函数解析式形式正是y=kx+b(k、b为常数,k≠0).当函数值为0时,即kx+b=0就与一元一次方程完全相同.
结论:由于任何一元一次方程都可转化为kx+b=0(k、b为常数,k≠0)的形式.所以解一元一次方程可以转化为:当一次函数值为0时,求相应的自变量的值.
从图象上看,这相当于已知直线y=kx+b确定它与x轴交点的横坐标值.
2.解一元一次不等式可以看作:当一次函数的函数值大(小)于0时,求自变量相应的取值范围.
【题型1 一次函数的与一元一次方程】
【例1】(2020秋 包河区期中)根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)关于x的方程kx+b=0的解;
(2)代数式k+b的值;
(3)关于x的方程kx+b=﹣3的解.
【解题思路】(1)利用函数图象写出函数值为0时对应的自变量的值即可;
(2)利用函数图象写出x=1时对应的函数值即可
(3)利用函数图象写出函数值为﹣3时对应的自变量的值即可.
【解答过程】解:(1)当x=2时,y=0,
所以方程kx+b=0的解为x=2;
(2)当x=1时,y=﹣1,
所以代数式k+b的值为﹣1;
(3)当x=﹣1时,y=﹣3,
所以方程kx+b=﹣3的解为x=﹣1.
【变式1-1】(2021秋 泰兴市校级期末)已知一次函数y=kx+1与yx+b的图象相交于点(2,5),求关于x的方程kx+b=0的解.
【解题思路】首先将(2,5)点代入一次函数解析式求出k,b的值,进而解方程得出答案.
【解答过程】解:∵一次函数y=kx+1与yx+b的图象相交于点(2,5),
∴5=2k+1,52+b,
解得:k=2,b=6,
则kx+b=0为:2x+6=0,
解得:x=﹣3.
【变式1-2】一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=4的解为多少?
【解题思路】先求出函数的解析式,再把y=4代入,即可求出x.
【解答过程】解:把(0,1)和(2,3)代入y=kx+b得:
,
解得:k=1,b=1,
即y=x+1,
当y=4时,x+1=4,
解得:x=3,
∴方程kx+b=4的解为x=3.
【变式1-3】已知一次函数y=kx﹣6的图象如图
(1)求k的值;
(2)在图中的坐标系中画出一次函数y=﹣3x+3的图象(要求:先列表,再描点,最后连线);
(3)根据图象写出关于x的方程kx﹣6=﹣3x+3的解.
【解题思路】(1)将点(4,0)代入y=kx﹣6,利用待定系数求出k的值;
(2)利用描点法画出一次函数y=﹣3x+3的图象;
(3)根据图象写出它们的交点坐标,即可得到关于x的方程kx﹣6=﹣3x+3的解.
【解答过程】解:(1)∵一次函数y=kx﹣6的图象过点(4,0),
∴4k﹣6=0,
∴k;
(2)列表:
描点:在平面直角坐标系中描出两点(0,3)、(1,0),
连线:过点(0,3)、(1,0)画直线,得出一次函数y=﹣3x+3的图象;
(3)一次函数y=kx﹣6与y=﹣3x+3的图象交于点(2,﹣3),
则关于x的方程kx﹣6=﹣3x+3的解为x=2.
【题型2 一次函数的与一元一次不等式(数形结合)】
【例2】(2021春 高明区期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:①对于函数y1=ax+b来说,y随x的增大而增大;②函数y=ax+d不经过第二象限;③不等式ax﹣d≥cx﹣b的解集是x≥4;④a﹣c(d﹣b),其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
【解题思路】根据题意和函数图象中的数据,可以判断各个小题中的结论是否成立,从而可以解答本题.
【解答过程】解:由图象可得,
对于函数y=ax+b来说,y随x的增大而增大,故①正确;
a>0,d>0,则函数y=ax+d经过第一、二、三象限,不经过第四象限,故②不正确;
由ax﹣d≥cx﹣b可得ax+b≥cx+d,故不等式ax﹣d≥cx﹣b的解集是x≥4,故③正确;
4a+b=4c+d可以得到a﹣c(d﹣b),故④正确;
故选:B.
【变式2-1】(2021 安徽模拟)已知一次函数y1=kx+3(k为常数,且k≠0)和y2=x﹣3.当x<2时,y1>y2,则k的取值范围是( )
A.﹣2≤k≤1且k≠0 B.k≤﹣2
C.k≥1 D.﹣2<k<1且k≠0
【解题思路】解不等式kx+3>x﹣3,根据题意得出k﹣1<0且2且k≠0,解此不等式即可.
【解答过程】解:∵一次函数y1=kx+3(k为常数,且k≠0)和y2=x﹣3,当x<2时,y1>y2,
∴kx+3>x﹣3,
∴kx﹣x>﹣6,
∴k﹣1<0且2且k≠0,
当k﹣1<0时,2时,k≥﹣2,
所以不等式组的解集为﹣2≤k<1且k≠0;
当k=1时,也成立,
故k的取值范围是﹣2≤k≤1且k≠0,
故选:A.
【变式2-2】(2021春 盐湖区校级期末)我们知道,若ab>0.则有或.如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)>0的解集是( )
A.x>2 B.﹣0.5<x<2
C.0<x<2 D.x<﹣0.5或x>2
【解题思路】由若不等式(kx+b)(mx+n)>0,则或,然后分类讨论,分别根据函数图象求得解集.
【解答过程】解:∵若ab>0.则有或,
∴若不等式(kx+b)(mx+n)>0,则或.
当,由图得:,此时该不等式无解.
当,由图得:,此时不等式组的解集为﹣0.5<x<2.
综上:﹣0.5<x<2.
故选:B.
【变式2-3】(2021春 中山市期末)一次函数y1=ax+b与y2=cx+d的图象如图所示,下列说法:
①对于函数y1=ax+b来说,y随x的增大而减小;
②函数y=ax+d的图象不经过第一象限;
③不等式ax+b>cx+d的解集是x>3;
④d﹣b=3(a﹣c).
其中正确的有( )
A.①③ B.②③④ C.①②④ D.②③
【解题思路】仔细观察图象:①根据函数图象直接得到结论;
②观察函数图象可以直接得到答案;
③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;
④根据两直线交点可以得到答案.
【解答过程】解:由图象可得:对于函数y1=ax+b来说,y随x的增大而减小,故①说法正确;
由于a<0,d<0,所以函数y2=ax+d的图象经过第二,三,四象限,即不经过第一象限,故②说法正确,
由图象可得当x<3时,一次函数y1=ax+b图象在y2=cx+d的图象上方,
∴ax+b>cx+d的解集是x<3,故③说法不正确;
∵一次函数y1=ax+b与y2=cx+d的图象的交点的横坐标为3,
∴3a+b=3c+d
∴3a﹣3c=d﹣b,
∴d﹣b=3(a﹣c).故④说法正确,
故选:C.
【题型3 一次函数的与一元一次不等式(取值范围)】
【例3】(2021春 海淀区期末)在平面直角坐标系xOy中,直线l:y1=x+1与直线l2:y2=2x﹣2交于点A.
(1)求点A的坐标;
(2)当y1>y2时,直接写出x的取值范围;
(3)已知直线l3:y3=kx+1,当x<3时,对于x的每一个值,都有y3>y2,直接写出k的取值范围.
【解题思路】(1)由直线l:y1=x+1与直线l2:y2=2x﹣2交于点A,故可联立方程组:得,故A(3,4).
(2)根据函数图象,可知:当y1>y2时,x<3.
(3)当x<3时,对于x的每一个值,都有y3>y2,故当x<3,y3﹣y2>0恒成立,得1≤k≤2.
【解答过程】解:(1)由题意得:
解得:
∴A(3,4).
(2)如图,当y1>y2时,x<3.
(3)当x<3,y3>y2恒成立,则x<3,y3﹣y2>0恒成立.
∵y3=kx+1,y2=2x﹣2,
∴y3﹣y2=(kx+1)﹣(2x﹣2)=(k﹣2)x+3.
∴若x<3,y3﹣y2>0恒成立,则[(k﹣2)x+3]min>0.
当k﹣2=0,即k=2,[(k﹣2)x+3]min=3>0.
当k﹣2>0,即k>2,[(k﹣2)x+3]min不存在.
当k﹣2<0,即k<2,[(k﹣2)x+3]min=3(k﹣2)+3≥0,故k≥1.
综上:1≤k≤2.
【变式3-1】(2021春 茌平区期末)已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1≥y2时x的取值范围.
【解题思路】(1)将两个函数的解析式联立得到方程组,解此方程组即可求出点A的坐标;
(2)先根据函数解析式求得B、C两点的坐标,可得BC的长,再利用三角形的面积公式可得结果;
(3)根据函数图象以及点A坐标即可求解.
【解答过程】解:(1)解方程组,得,
所以点A坐标为(1,﹣3);
(2)当y1=0时,﹣x﹣2=0,x=﹣2,则B点坐标为(﹣2,0);
当y2=0时,x﹣4=0,x=4,则C点坐标为(4,0);
∴BC=4﹣(﹣2)=6,
∴△ABC的面积6×3=9;
【变式3-2】(2021春 海珠区期末)已知一次函数y1=ax+b的图象交x轴和y轴于点B和D;另一个一次函数y2=bx+a的图象交x轴和y轴于点C和E,且两个函数的图象交于点A(1,4)
(1)当a,b为何值时,y1和y2的图象重合;
(2)当0<a<4,且在x<1时,则y1>y2成立.求b的取值范围;
【解题思路】(1)把A(1,4)代入y1=ax+b求得a+b=4,得到b=4﹣a,于是得到结论;
(2)根据题意列不等式即可得到结论;
【解答过程】解:(1)∵y1=ax+b的图象过点A(1,4),
∴a+b=4,
∴b=4﹣a,
∴y1=ax+(4﹣a),y2=(4﹣a)x+a,
∵y1和y2的图象重合,
∴a=4﹣a,
∴a=2,b=2;
即当a=2,b=2时,y1和y2的图象重合;
(2)∵a+b=4,如图1,
∴a=4﹣b,
∴y1=(4﹣b)x+b,
y2=bx+(4﹣b),
∵0<a<4,0<4﹣b<4且x<1时,y1>y2成立,
∴由图象得4﹣b<b,
∴2<b<4;
【变式3-3】(2020春 赣县区期末)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(﹣2,4),且与正比例函数yx的图象交于点B(a,2).
(1)求a的值及一次函数y=kx+b的解析式;
(2)若一次函数y=kx+b的图象与x轴交于点C,且正比例函数yx的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
(3)直接写出关于x的不等式0x<kx+b的解集.
【解题思路】(1)先确定B的坐标,然后根据待定系数法求解析式;
(2)先求得C的坐标,然后根据题意求得平移后的直线的解析式,把C的坐标代入平移后的直线的解析式,即可求得M的值;
(3)找出直线yx落在y=kx+b的下方且在x轴上方的部分对应的x的取值范围即可.
【解答过程】解:(1)∵正比例函数yx的图象经过点B(a,2),
∴2a,解得,a=﹣3,
∴B(﹣3,2),
∵一次函数y=kx+b的图象经过点A(﹣2,4),B(﹣3,2),
∴,解得,
∴一次函数y=kx+b的解析式为y=2x+8;
(2)∵一次函数y=2x+8的图象与x轴交于点C,
∴C(﹣4,0),
∵正比例函数yx的图象向下平移m(m>0)个单位长度后经过点C,
∴平移后的函数的解析式为yx﹣m,
∴0(﹣4)﹣m,解得m;
(3)∵一次函y=kx+b与正比例函数yx的图象交于点B(﹣3,2),
且一次函数y=2x+8的图象与x轴交于点C(﹣4,0),
∴关于x的不等式0x<kx+b的解集是﹣3<x<0.
【题型4 一次函数与一元一次不等式(面积问题)】
【例4】(2021春 诸城市期末)如图,直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3);直线y=1﹣mx分别与x轴交于点C,与直线AB交于点D,已知关于x的不等式kx+b>1﹣mx的解集是x.
(1)分别求出k,b,m的值;
(2)求S△ACD.
【解题思路】(1)首先利用待定系数法确定直线的解析式,然后根据关于x的不等式kx+b>1﹣mx的解集是x得到点D的横坐标为,再将x代入yx+3,得:y,将x,y代入y=1﹣mx求得m=1即可;
(2)先确定直线与x轴的交点坐标,然后利用三角形的面积公式计算即可.
【解答过程】解:(1)∵直线y=kx+b分别与x轴、y轴交于点A(﹣2,0),B(0,3),
,
解得:k,b=3,
∵关于x的不等式kx+b>1﹣mx的解集是x,
∴点D的横坐标为,
将x代入yx+3,得:y,
∴D(,),
将x,y代入y=1﹣mx,
解得:m=1;
(2)如图,过点D作DH⊥AC于H,则DH
对于y=1﹣x,令y=0,得:x=1,
∴点C的坐标为(1,0),
∴S△ACD AC DH[1﹣(﹣2)].
【变式4-1】(2021春 东辽县期末)已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x﹣4与x轴于D,与直线AB相交于点C.
(1)求点C的坐标;
(2)根据图象,写出关于x的不等式2x﹣4>kx+5的解集;
(3)求△ADC的面积.
【解题思路】(1)根据点A的坐标利用待定系数法可求出直线AB的解析式,联立直线AB、CD的解析式成方程组,通过解方程组即可求出点C的坐标;
(2)根据直线AB、CD的上下位置关系结合点C的坐标,即可得出不等式2x﹣4>kx+5的解集;
(3)利用一次函数图象上点的坐标特征可求出点D的坐标,再根据三角形的面积公式即可求出△ADC的面积.
【解答过程】解:(1)∵直线y=kx+5经过点A(5,0),
∴5k+5=0,
解得:k=﹣1,
∴直线AB的解析式为y=﹣x+5.
联立直线AB、CD的解析式成方程组,
,解得:,
∴点C的坐标为(3,2).
(2)观察函数图象可知:当x>3时,直线y=2x﹣4在直线y=﹣x+5的上方,
∴不等式2x﹣4>kx+5的解集为x>3.
(3)当y=2x﹣4=0时,x=2,
∴点D的坐标为(2,0),
∴S△ACD(xA﹣xD) yC(5﹣2)×2=3.
【变式4-2】(2020春 宁化县校级月考)如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P(a,2).
(1)求出不等式2x≤kx+3的解集;
(2)求出△OAP的面积.
【解题思路】(1)利用一次函数图象上点的坐标特征先求出a的值,然后观察函数图象,写出直线y=kx+3在直线y=2x上方所对应的自变量的取值范围即可;
(2)先求出直线l2的解析式,再求出A点坐标,然后利用三角形面积公式求解.
【解答过程】解:(1)把P(a,2)代入y=2x得2a=2,解得a=1,则P(1,2),
当x≤1时,2x≤kx+3,
所以不等式2x≤kx+3的解集为x≤1;
(2)把P(1,2)代入y=kx+3得k+3=2,解得k=﹣1,
所以直线l2的解析式为y=﹣x+3,当y=0时,﹣x+3=0,解得x=3,则A(3,0),
所以△OAP的面积2×3=3.
【变式4-3】已知一次函数y1=﹣2x﹣3与y2x+2.
(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3x+2的解集为 x<﹣2 ;
(3)求两图象和y轴围成的三角形的面积.
【解题思路】(1)先求出直线y1=﹣2x﹣3,y2x+2与x轴和y轴的交点,再画出两函数图象即可;
(2)直线y1=﹣2x﹣3的图象落在直线y2x+2上方的部分对应的x的取值范围就是不等式﹣2x﹣3x+2的解集;
(3)根据三角形的面积公式求解即可.
【解答过程】解:(1)函数y1=﹣2x﹣3与x轴和y轴的交点分别是(﹣1.5,0)和(0,﹣3),
y2x+2与x轴和y轴的交点分别是(﹣4,0)和(0,2),
其图象如图:
(2)观察图象可知,函数y1=﹣2x﹣3与y2x+2交于点(﹣2,1),
当x<﹣2时,直线y1=﹣2x﹣3的图象落在直线y2x+2的上方,即﹣2x﹣3x+2,
所以不等式﹣2x﹣3x+2的解集为x<﹣2;
故答案为x<﹣2;
(3)∵y1=﹣2x﹣3与y2x+2与y轴分别交于点A(0,﹣3),B(0,2),
∴AB=5,
∵y1=﹣2x﹣3与y2x+2交于点C(﹣2,1),
∴△ABC的边AB上的高为2,
∴S△ABC5×2=5.
【题型5 一次函数的与一元一次不等式(求点的坐标)】
【例5】如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4),且MN=5.
(1)求直线MN的解析式;
(2)根据图象,写出不等式kx+b≥0的解集;
(3)若点P在x轴上,且点P到直线y=kx+b的距离为,直接写出符合条件的点P的坐标.
【解题思路】(1)把点M、N的坐标分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值;
(2)直线y=kx+b在x轴及其上方的部分对应的x的取值范围即为所求;
(3)作△OMN的高OA.根据三角形的面积公式求出OA,则点P的坐标是(0,0);在x轴上作O关于M的对称点为(6,0),易得(6,0)到直线y=kx+b的距离也为.
【解答过程】解:(1)∵直线y=kx+b与坐标轴相交于点M(3,0),N(0,4),
所以,
解得:,
∴直线MN的解析式为:yx+4;
(2)根据图形可知,当x≤3时,y=kx+b在x轴及其上方,即kx+b≥0,
则不等式kx+b≥0的解集为x≤3;
(3)如图,作△OMN的高OA.
∵S△OMNMN OAOM ON,
∴OA,
∴点P的坐标是(0,0);
在x轴上作O关于M的对称点为(6,0),易得(6,0)到直线y=kx+b的距离也为,
所以点P的坐标是(0,0)或(6,0).
【变式5-1】(2021春 顺德区期末)一次函数y1=kx+b和y2=﹣4x+a的图象如图所示,且A(0,4),C(﹣2,0).
(1)由图可知,不等式kx+b>0的解集是 x>﹣2 ;
(2)若不等式kx+b>﹣4x+a的解集是x>1.
①求点B的坐标;
②求a的值.
【解题思路】(1)根据函数图象和题意可以直接写出不等式kx+b>0的解集;
(2)①由题意可以求得k、b的值,然后将x=1代入y1=kx+b即可求得点B的坐标;
②根据点B也在函数y2=﹣4x+a的图象上,从而可以求得a的值.
【解答过程】解:(1)∵A(0,4),C(﹣2,0)在一次函数y1=kx+b上,
∴不等式kx+b>0的解集是x>﹣2,
故答案为:x>﹣2;
(2)①∵A(0,4),C(﹣2,0)在一次函数y1=kx+b上,
∴,得,
∴一次函数y1=2x+4,
∵不等式kx+b>﹣4x+a的解集是x>1,
∴点B的横坐标是x=1,
当x=1时,y1=2×1+4=6,
∴点B的坐标为(1,6);
②∵点B(1,6),
∴6=﹣4×1+a,得a=10,
即a的值是10.
【变式5-2】(2020秋 南京期末)已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的函数关系式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,直接写出当x在什么范围内,不等式2x﹣4>kx+b.
【解题思路】(1)利用待定系数法即可求得函数的解析式;
(2)解两个函数解析式组成方程组即可求解;
(3)关于x的不等2x﹣4>kx+b的解集就是函数y=kx+b的图象在下边的部分自变量的取值范围.
【解答过程】解:(1)根据题意得,
解得,
则直线AB的解析式是y=﹣x+5;
(2)根据题意得,
解得:,
则C的坐标是(3,2);
(3)根据图象可得不等式的解集是x>3.
【变式5-3】在平面直角坐标系中,直线y=﹣2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=﹣2x+1交于点B,设点B的横坐标为﹣2.
(1)求点B的坐标及k的值;
(2)求直线y=﹣2x+1、直线y=x+k与y轴所围成的△ABC的面积;
(3)根据图象直接写出不等式﹣2x+1>x+k的解集.
【解题思路】(1)对于y=﹣2x+1,计算自变量为﹣2时的函数值可得到B点坐标,然后把B点坐标代入y=x+k可得到k的值;
(2)先确定两直线与y轴的交点A、C的坐标,然后利用三角形面积公式求解;
(3)观察函数图象,写出直线y=﹣2x+1在直线y=x+k上方所对应的自变量的范围即可.
【解答过程】解:(1)当x=﹣2时,y=﹣2×(﹣2)+1=5,则B(﹣2,5).
把B(﹣2,5)代入y=x+k得﹣2+k=5,解得k=7;
(2)当x=0时,y=﹣2x+1=1,则C(0,1);
当x=0时,y=x+7=7,则A(0,7)
所以AC=7﹣1=6,
所以S△ABC6×2=6;
(3)x<﹣2.
【知识点2 一次函数与二元一次方程】
(1)每个二元一次方程都对应一个一次函数,也对应一条直线.
(2)解二元一次方程组,从“数”的角度看,相当于考虑当自変量为何值时两个函数的值相等,以及这个函数值是多少,从“形”的角度看,相当于确定两条直线的交点坐标.
【题型6 一次函数与二元一次方程】
【例6】(2021 济南二模)中国古代数学专著《九章算术》“方程”一章记载用算筹(方阵)表示二元一次方程组的方法,发展到现代就是用矩阵式来表示二元一次方程组,而该方程组的解就是对应两直线(不平行)a1x+b1y=c1与a2x+b2y=c2的交点坐标P(x,y).据此,则矩阵式所对应两直线交点坐标是 (2,5) .
【解题思路】根据题意得出方程组,求出方程组的解,再得出答案即可.
【解答过程】解:根据题意得:
,
①+②,得x=2,
把x=2代入①,得8﹣y=3,
解得:y=5,
所以方程组的解为,
∴两直线交点坐标是(2,5),
故答案为:(2,5).
【变式6-1】如图,直线y=﹣2x+6与直线y=mx+n相交于点M(p,4).
(1)求p的值;
(2)直接写出关于x,y的二元一次方程组的解;
(3)判断直线y=3nx+m﹣2n是否也过点M?并说明理由.
【解题思路】(1)根据直线y=﹣2x+6经过点M,即可求出p.
(2)由图象可知交点的坐标就是方程组的解.
(3)先求出m+n=4,用代入法可以解决.
【解答过程】解:(1)∵直线y=﹣2x+6经过点M(p,4),
∴4=﹣2p+6,
∴p=1.
(2)由图象可知方程组的解为,
(3)结论:直线y=3nx+m﹣2n经过点M,理由如下:
∵点M(1,4)在直线y=mx+n上,
∴m+n=4,
∴当x=1,时,y=3nx+m﹣2n=m+n=4,
∴直线y=3nx+m﹣2n经过点M.
【变式6-2】(2021秋 文成县期末)如图,l1,l2分别表示两个一次函数的图象,它们相交于点P,
(1)求出两条直线的函数关系式;
(2)点P的坐标可看作是哪个二元一次方程组的解;
(3)求出图中△APB的面积.
【解题思路】(1)由图可得两函数与坐标轴的交点坐标,用待定系数法可求出它们的函数解析式;
(2)联立两个一次函数的解析式,所得方程组的解即为P点坐标.
(3)△ABP中,以AB为底,P点横坐标的绝对值为高,可求出△ABP的面积.
【解答过程】解:(1)设直线l1的解析式是y=kx+b,已知l1经过点(0,3),(1,0),
可得:,解得,
则函数的解析式是y=﹣3x+3;
同理可得l2的解析式是:y=x﹣2.
(2)点P的坐标可看作是二元一次方程组的解.
(3)易知:A(0,3),B(0,﹣2),P(,);
∴S△APBAB |xP|5.
【变式6-3】(2020秋 西安期末)学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2,且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
(1)当参加老师的人数为多少时,两家旅行社收费相同?
(2)当参加老师的人数为多少人时,选择甲旅行社合算?
(3)如果全共有50人参加时,选择哪家旅行社合算?
【解题思路】(1)当两函数图象相交时,两家旅行社收费相同,由图象即可得出答案.
(2)由图象比较收费y1、y2,即可得出答案.
(3)当有50人时,比较收费y1、y2,即可得出答案.
【解答过程】解:(1)当两函数图象相交时,两家旅行社收费相同,由图象知为30人;
(2)由图象知:当有30人以下时,y1<y2,所以选择甲旅行社合算;
(3)由图象知:当有50人参加时,y1>y2,所以选择乙旅行社合算;
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
