第五章一次函数专题5.5 一次函数的应用-重难点题型(含解析)
文档属性
| 名称 | 第五章一次函数专题5.5 一次函数的应用-重难点题型(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 16:27:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
一次函数的应用6大题型
【知识点1 一次函数与实际问题】
在研究有关一次函数的实际问题时,要遵循一审、二设、三列、四解的方法:
第1步:审题。认真读题,分析题中各个量之间的关系;
第2步:设自变量。根据各个量之间的关系设满足题意的自变量;
第3步:列函数。根据各个量之间的关系列出函数;
第4步:求解。求出满足题意的数值。
【题型1 一次函数的应用(行程问题)】
【例1】(2021春 海门市期中)甲、乙两人分别从笔直道路上的A、B两地同时出发相向匀速而行,已知甲比乙先出发6分钟,两人在C地相遇,相遇后甲立即按原速原路返回A地,乙继续向A地前行,约定先到A地者停止运动就地休息.若甲、乙两人相距的路程y(米)与甲行走的时间x(分钟)之间的关系如图所示,有下列说法:①甲的速度是60米/分钟,乙的速度是80米/分钟;②甲出发30分钟时,两人在C地相遇;③乙到达A地时,甲与A地相距450米,其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
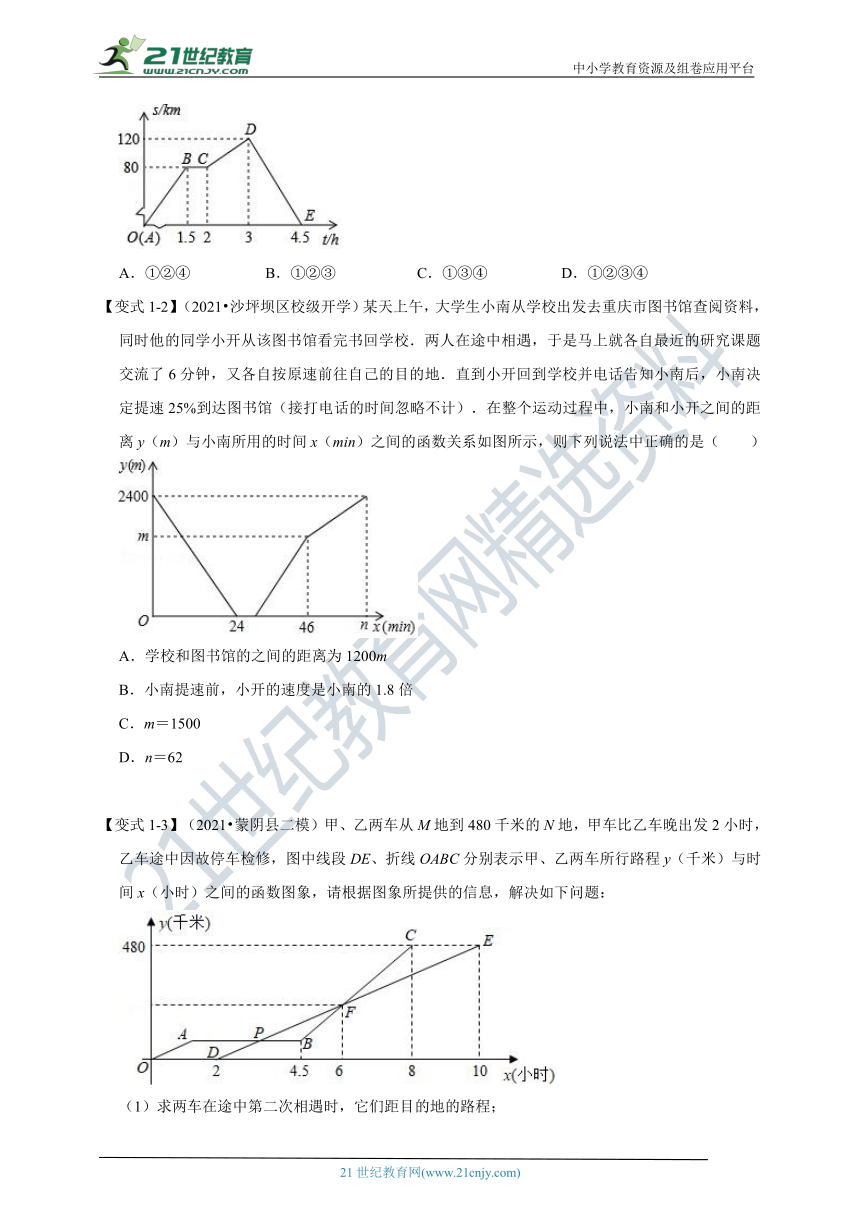
【变式1-1】(2021春 巴彦淖尔期末)如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,判断下列结论正确的选项是( )
①汽车在行驶途中停留了0.5h;
②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;
④汽车出发4h离出发地40km.
A.①②④ B.①②③ C.①③④ D.①②③④
【变式1-2】(2021 沙坪坝区校级开学)某天上午,大学生小南从学校出发去重庆市图书馆查阅资料,同时他的同学小开从该图书馆看完书回学校.两人在途中相遇,于是马上就各自最近的研究课题交流了6分钟,又各自按原速前往自己的目的地.直到小开回到学校并电话告知小南后,小南决定提速25%到达图书馆(接打电话的时间忽略不计).在整个运动过程中,小南和小开之间的距离y(m)与小南所用的时间x(min)之间的函数关系如图所示,则下列说法中正确的是( )
A.学校和图书馆的之间的距离为1200m
B.小南提速前,小开的速度是小南的1.8倍
C.m=1500
D.n=62
【变式1-3】(2021 蒙阴县二模)甲、乙两车从M地到480千米的N地,甲车比乙车晚出发2小时,乙车途中因故停车检修,图中线段DE、折线OABC分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数图象,请根据图象所提供的信息,解决如下问题:
(1)求两车在途中第二次相遇时,它们距目的地的路程;
(2)甲车出发多长时间,两车在途中第一次相遇?
【题型2 一次函数的应用(调运问题)】
【例2】(2021春 大安市期末)A城有肥料400吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡镇,从A城运往C、D两乡镇肥料费为20元/吨和25元/吨;从B城往C、D两乡镇运肥料的费用分别为15元/吨和24元/吨,C乡镇需要肥料340吨,D乡镇需要肥料360吨.设A城运往C乡镇x吨肥料,请解答下列问题:
(1)根据题意,填写下列表格:
城、乡/吨数 C D
A x
B
(2)设总运费为W(元),求出W(元)与x(吨)的函数关系式,并写出自变量的取值范围;
(3)求怎样调运可使总运费最少?最少为多少元?
【变式2-1】(2021 寻乌县模拟)疫情期间,甲、乙两个仓库要向M,N两地运送防疫物资,已知甲仓库可调出50吨防疫物资,乙仓库可调出40吨防疫物资,M地需35吨防疫物资,N地需55吨防疫物资,两仓库到M,N两地的路程和运费如下表:
路程/千米 运送1千米所需运费/(元/吨)
甲仓库 乙仓库 甲仓库 乙仓库
M地 20 15 12 12
N地 25 20 10 8
(1)设从甲仓库运往M地防疫物资x吨,两仓库运往M,N两地的总费用为y元,求y关于x的函数关系式.
(2)如何调运才能使总运费最少?总运费最少是多少?
【变式2-2】(2021春 满洲里市期末)已知A地有蔬菜200t,B地有蔬菜300t,现决定将这些蔬菜全部调运给C,D两地,C,D两地分别需要调运蔬菜240t和260t.其中从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C地的蔬菜为x吨.设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案.
【变式2-3】(2021春 昆明期末)某市A、B两个仓库分别有救灾物资200吨和300吨,2021年5月18日起云南大理州漾濞县已连续发生多次地震,最高震级为5月21日发生的6.4级地震,为援助灾区,现需将这些物资全部运往甲,乙两个受灾村.已知甲村需救灾物资240吨,乙村需救灾物资260吨,从A仓库运往甲,乙两村的费用分别为每吨20元和每吨25元,从B仓库运往甲,乙两村的费用分别为每吨15元和24元.设A仓库运往甲村救灾物资x吨,请解答下列问题:
(1)根据题意,填写下表格:
仓库 甲村 乙村
A x ①
B ② ③
①= ;②= ;③= .
(2)设总运费为W(元),求出W(元)与x(吨)的函数关系式.
(3)求怎么调运可使总运费最少?最少运费为多少元?
【题型3 一次函数的应用(利润最大化)】
【例3】(2021 镇雄县二模)2020年6月1日上午,国务院总理在山东烟台考察时表示,地摊经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机.“地摊经济”成为了社会关注的热门话题.小明从市场得知如表信息:
甲商品 乙商品
进价(元/件) 35 5
售价(元/件) 45 8
小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
(1)求出y与x之间的函数关系式;
(2)小明用不超过2000元资金一次性购进甲,乙两种商品,求x的取值范围;
(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于632.5元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大.
【变式3-1】(2021 青白江区模拟)在近期“抗疫”期间,某药店销售A,B两种型号的口罩,已知销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍,则该药店购进A型、B型口罩各多少只,才能使销售总利润y最大?
【变式3-2】(2021春 连山区期末)由于新能源汽车越来越受到消费者的青睐,某经销商决定分两次购进甲、乙两种型号的新能源汽车(两次购进同一种型号汽车的每辆的进价相同).第一次用270万元购进甲型号汽车30辆和乙型号汽车20辆;第二次用128万元购进甲型号汽车14辆和乙型号汽车10辆.
(1)求甲、乙两种型号汽车每辆的进价;
(2)经销商分别以每辆甲型号汽车8.8万元,每辆乙型号汽车4.2万元的价格销售后,根据销售情况,决定再次购进甲、乙两种型号的汽车共100辆,且乙型号汽车的数量不少于甲型号汽车数量的3倍,设再次购进甲型汽车a辆,这100辆汽车的总销售利润为W万元.
①求W关于a的函数关系式;并写出自变量的取值范围;
②若每辆汽车的售价和进价均不变,该如何购进这两种汽车,才能使销售利润最大?最大利润是多少?
【变式3-3】(2021 鹿邑县一模)草莓是一种极具营养价值的水果,当下正是草莓的销售旺季.某水果店以2850元购进两种不同品种的盒装草莓.若按标价出售可获毛利润1500元(毛利润=售价﹣进价),这两种盒装草莓的进价、标价如表所示:
价格/品种 A品种 B品种
进价(元/盒) 45 60
标价(元/盒) 70 90
(1)求这两个品种的草莓各购进多少盒;
(2)该店计划下周购进这两种品种的草莓共100盒(每种品种至少进1盒),并在两天内将所进草莓全部销售完毕(损耗忽略不计).因B品种草莓的销售情况较好,水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒.如何安排进货,才能使毛利润最大,最大毛利润是多少?
【题型4 一次函数的应用(费用最低)】
【例4】(2021春 广安期末)为积极响应垃圾分类的号召,某街道决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱.已知购买3个垃圾箱和2个温馨提示牌需要280元,购买2个垃圾箱和3个温馨提示牌需要270元.
(1)每个垃圾箱和每个温馨提示牌各多少元?
(2)若购买垃圾箱和温馨提示牌共100个(两种都买),且垃圾箱的个数不少于温馨提示牌个数的3倍,请写出总费用w(元)与垃圾箱个数m(个)之间的函数关系式,并说明当购买垃圾箱和温馨提示牌各多少个时,总费用最低,最低费用为多少元?
【变式4-1】(2021春 环江县期末)某县园林局打算购买三角梅、水仙装点城区道路,负责人小李去花卉基地调查发现:购买1盆三角梅和2盆水仙需要14元,购买2盆三角梅和1盆水仙需要13元.
(1)求三角梅、水仙的单价各是多少元?
(2)购买三角梅、水仙共10000盆,且购买的三角梅不少于3000盆,但不多于5000盆.
①设购买的三角梅种花a盆,总费用为W元,求W与a的关系式;
②当总费用最少时,应选择哪一种购买方案?最少费用为多少元?
【变式4-2】(2021 三水区校级二模)截至2021年4月10日,全国累计报告接种新冠疫苗16447.1万剂次,接种总剂次数为全球第二.某社区有80000人每人准备接种两剂次相同厂家生产的新冠疫苗并被分配到A、B两个接种点,A接种点有5个接种窗口,B接种点有4个接种窗口.每个接种窗口每天的接种量相同,并且在独立完成20000人的两剂次新冠疫苗接种时,A接种点比B接种点少用5天.
(1)求A、B两个接种点每天接种量;
(2)设A接种点工作x天,B接种点工作y天,刚好完成该社区80000人的新冠疫苗接种任务,求y关于x的函数关系式;
(3)在(2)的条件下,若A接种点每天耗费6.5万元,B接种点每天耗费为4万元,且A、B两个接种点的工作总天数不超过85天,则如何安排A、B两个接种点工作的天数,使总耗费最低?并求出最低费用.
【变式4-3】(2021春 大同期末)在新冠疫情防控期间,某校新购进A、B两种型号的电子体温测量仪共20台,其中A型仪器的数量不少于B型仪器的,已知A、B两种测温仪的价格如表所示,请问购买A、B两种测温仪各多少台时,可使所购仪器的总费用最少?最少需多少元?
型号 A B
价格 800元/台 600元/台
【题型5 一次函数的应用(工程问题)】
【例5】(2021 汇川区三模)为了主题为“醉美遵义,酒都仁怀”第十三届遵义文化旅游产业发展大会召开,仁怀某社区计划对面积为2000m2的区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2.5倍,并且在独立完成面积为500m2区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数解析式.
(3)若甲队每天绿化费用是1.5万元,乙队每天绿化费用为0.5万元,且甲乙两队施工的总天数不超过19天,则如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低费用.
【变式5-1】(2021春 青羊区期末)甲、乙两个工程队分别同时铺设两条公路,所铺设公路的长度y(m)与铺设时间x(h)之间的关系如图所示,根据图象所提供的信息分析,解决下列问题:
(1)在2时~6时段时,乙队的工作效率为 5 m/h;
(2)分别求出乙队在0时~2时段和2时~6时段,y与x的关系式,并求出甲乙两队所铺设公路长度相等时x的值;
(3)求出当两队所铺设的公路长度之差为5m时x的值.
【变式5-2】(2021春 沙坪坝区校级期末)甲、乙两人同时开始共同组装一批零件,工作两小时后,乙因事离开,停止工作.一段时间后,乙重新回到岗位并提高了工作效率.最后40分钟,甲休息,由乙独自完成剩余零件的组装.甲在工作过程中工作效率保持不变,乙在每个工作阶段的工作效率保持不变.甲、乙两人组装零件的总数y(个)与工作时间x(小时)之间的图象如图.
(1)这批零件一共有多少个?
(2)在整个组装过程中,当甲、乙各自组装的零件总数相差40个时,求x的值.
【变式5-3】(2020秋 郑州期末)工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间t(时),甲组加工零件的数量为y甲(个),乙组加工零件的数量为y乙(个),其函数图象如图所示.
(1)求y乙与t之间的函数关系式,并写出t的取值范围;
(2)求a的值,并说明a的实际意义;
(3)甲组加工多长时间时,甲、乙两组加工零件的总数为480个.
【题型6 一次函数的应用(其他问题)】
【例6】(2021春 沙河口区期末)为预防疫情传播,学校对教室定期喷药消毒.如图为一次消毒中,某教室每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)的函数图象,它是由关闭门窗集中喷药,通风前和打开门窗后通风三段不同的一次函数组成的.在下面四个选项中,错误的是( )
A.经过5min集中喷药,教室每立方米空气中含药量最高达到10mg/m3
B.持续11min室内空气中的含药量不低于8mg/m3
C.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才有效杀灭病毒.由此判断此次消毒有效
D.当室内空气中的含药量低于4mg/m3时,对人体是安全的.从室内空气中的含药量达到10mg/m3开始,需经过40min后学生才能进入室内
【变式6-1】(2021春 朝阳区校级期末)某地自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.
(1)某月该单位用水3200吨,水费是 元;若用水2800吨,水费是 元;
(2)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式;
(3)若某月该单位缴纳水费1540元,则该单位这个月的用水量为多少吨?
【变式6-2】(2021春 河东区期末)一个水库的水位在某段时间内持续上涨,表格中记录了连续5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
0 1 2 3 4 5
3 3.3 3.6 3.9 4.2 4.5
(1)水位高度y是否为时间x的函数?若是,请求出这个函数解析式;
(2)据估计,这种上涨规律还会持续,并且当水位高度达到8m时,水库报警系统会自动发出警报.请预测再过多久系统会发出警报?
【变式6-3】(2021 涧西区三模)某大型商场为了提高销售人员的积极性,对原有的薪酬计算方式进行了修改,设销售人员一个月的销售量为x(件),销售人员的月收入为y(元),原有的薪酬计算方式y1元采用的是底薪+提成的方式,且y1=k1x+b,已知每销售一件商品另外获得15元的提成修改后的薪酬计算方式为y2(元),且y2=k2x+b,根据图象回答下列问题:
(1)求y1和y2的解析式,并说明b的实际意义;
(2)求两个函数图象的交点F的坐标,并说明交点F的实际意义;
(3)根据函数图象请判断哪种薪酬计算方式更适合销售人员.
一次函数的应用-重难点题型
【知识点1 一次函数与实际问题】
在研究有关一次函数的实际问题时,要遵循一审、二设、三列、四解的方法:
第1步:审题。认真读题,分析题中各个量之间的关系;
第2步:设自变量。根据各个量之间的关系设满足题意的自变量;
第3步:列函数。根据各个量之间的关系列出函数;
第4步:求解。求出满足题意的数值。
【题型1 一次函数的应用(行程问题)】
【例1】(2021春 海门市期中)甲、乙两人分别从笔直道路上的A、B两地同时出发相向匀速而行,已知甲比乙先出发6分钟,两人在C地相遇,相遇后甲立即按原速原路返回A地,乙继续向A地前行,约定先到A地者停止运动就地休息.若甲、乙两人相距的路程y(米)与甲行走的时间x(分钟)之间的关系如图所示,有下列说法:①甲的速度是60米/分钟,乙的速度是80米/分钟;②甲出发30分钟时,两人在C地相遇;③乙到达A地时,甲与A地相距450米,其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
【解题思路】根据图象可知A、B两地相距3720米;利用速度=路程÷时间可求出甲、乙的速度,由二者相遇的时间=6+A、B两地之间的路程÷二者速度和,可求出二者相遇的时间,再由A、C两地之间的距离=甲的速度×二者相遇的时间可求出A、C两地之间的距离,由A、C两地之间的距离结合甲、乙的速度,可求出乙到达A地时甲与A地相距的路程.
【解答过程】解:由图象可知,A、B两地相距3720米,
甲的速度为(3720﹣3360)÷6=60(米/分钟),
乙的速度为(3360﹣1260)÷(21﹣6)﹣60=80(米/分钟),故①说法正确;
甲、乙相遇的时间为6+3360÷(60+80)=30(分钟),故②说法正确;
A、C两地之间的距离为60×30=1800(米),
乙到达A地时,甲与A地相距的路程为1800﹣1800÷80×60=450(米).故③说法正确.
即正确的说法有4个.
故选:D.
【变式1-1】(2021春 巴彦淖尔期末)如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,判断下列结论正确的选项是( )
①汽车在行驶途中停留了0.5h;
②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;
④汽车出发4h离出发地40km.
A.①②④ B.①②③ C.①③④ D.①②③④
【解题思路】根据停留时距离S不发生变化可判断①;根据速度=路程÷时间列式计算即可判断②;求得往返的路程和得出答案即可判断③;先求出3h到4.5h的速度,再求据出发地的距离可判断④.
【解答过程】解:①汽车在行驶途中停留了2﹣1.5=0.5h,
故①正确;
②平均速度:120×2÷4.5千米/小时,
故②错误;
③汽车共行驶了120×2=240km,
故③正确;
④汽车自出发后3h到4.5h速度为:120÷(4.5﹣3)=120÷1.5=80千米/小时,
∴汽车出发4h离出发地距离为120﹣(4﹣3)×80=120﹣80=40千米,
故④正确.
∴正确的是①③④,
故选:C.
【变式1-2】(2021 沙坪坝区校级开学)某天上午,大学生小南从学校出发去重庆市图书馆查阅资料,同时他的同学小开从该图书馆看完书回学校.两人在途中相遇,于是马上就各自最近的研究课题交流了6分钟,又各自按原速前往自己的目的地.直到小开回到学校并电话告知小南后,小南决定提速25%到达图书馆(接打电话的时间忽略不计).在整个运动过程中,小南和小开之间的距离y(m)与小南所用的时间x(min)之间的函数关系如图所示,则下列说法中正确的是( )
A.学校和图书馆的之间的距离为1200m
B.小南提速前,小开的速度是小南的1.8倍
C.m=1500
D.n=62
【解题思路】从图象上直接可以得出图书馆到学校的距离,从而可以判断A;先求出小南和小开的和速度,再求出小开的速度,从而可以判断B;通过图象和题意可以求出m,从而可以判断C;先求出小南提速后的速度,再根据路程÷速度=时间,即可判断D.
【解答过程】解:由图象可知:图书馆到学校的距离为2400米,
故A错误;
小南和小开的和速度为:2400÷24=100(米/分),
小开走完2400米所用时间为:46﹣6=40(分),
∴小开的速度为:2400÷40=60(米/分),
∴小南的速度为:100﹣60=40(米/分),
∴小南提速前,小开的速度是小南的60÷40=1.5,
故B错误;
相遇后到小开到达学校所用时间为46﹣(24+6)=16(分),
∴m=100×16=1600(米),
故C错误;
小南提速后的速度为40(1+25%)=50(米/分),
∴n=(2400﹣1600)÷50+46=16+46=62(分),
故D正确.
故选:D.
【变式1-3】(2021 蒙阴县二模)甲、乙两车从M地到480千米的N地,甲车比乙车晚出发2小时,乙车途中因故停车检修,图中线段DE、折线OABC分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数图象,请根据图象所提供的信息,解决如下问题:
(1)求两车在途中第二次相遇时,它们距目的地的路程;
(2)甲车出发多长时间,两车在途中第一次相遇?
【解题思路】(1)设甲车所行使路程y与时间x的函数关系式为y=k1x+b1,利用待定系数法求出其函数关系式,再结合交点F的横坐标解答即可;
(2)求出线段BC对应的函数关系式,求出点P的坐标,计算两车在途中第一次相遇的时间.
【解答过程】解:(1)设甲车所行使路程y与时间x的函数关系式为y=k1x+b1,
把(2,0)和(10,480)代入,得,
解得:,
∴y与x的函数关系式为y=60x﹣120;
由图可得,交点F表示第二次相遇,F点的横坐标为6,此时y=60×6﹣120=240,
∴F(6,240),
故两车在途中第二次相遇时它们距目的地的路程为480﹣240=240(千米);
(2)设线段BC对应的函数关系式为y=k2x+b2,
把(6,240)、(8,480)代入,得,
解得,
故y与x的函数关系式为y=120x﹣480,
则当x=4.5时,y=120×4.5﹣480=60.
可得:点B的纵坐标为60,
∵线段AB表示因故停车检修,
∴交点P的纵坐标为60,
把y=60代入y=60x﹣120中,
有60=60x﹣120,
解得x=3,
则交点P的坐标为(3,60),
∵交点P表示第一次相遇,
∴甲车出发的时间为:3﹣2=1(小时).
【题型2 一次函数的应用(调运问题)】
【例2】(2021春 大安市期末)A城有肥料400吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡镇,从A城运往C、D两乡镇肥料费为20元/吨和25元/吨;从B城往C、D两乡镇运肥料的费用分别为15元/吨和24元/吨,C乡镇需要肥料340吨,D乡镇需要肥料360吨.设A城运往C乡镇x吨肥料,请解答下列问题:
(1)根据题意,填写下列表格:
城、乡/吨数 C D
A x 400﹣x
B 340﹣x x﹣40
(2)设总运费为W(元),求出W(元)与x(吨)的函数关系式,并写出自变量的取值范围;
(3)求怎样调运可使总运费最少?最少为多少元?
【解题思路】(1)根据题意,可以将表格补充完整;
(2)根据题意和(1)中表格的数据,可以写出W(元)与x(吨)的函数关系式,并写出自变量的取值范围;
(3)根据(2)中函数关系式和一次函数的性质,可以得到怎样调运可使总运费最少,最少为多少元.
【解答过程】解:(1)根据题意,表格填写如下:
城、乡/吨数 C D
A x 400﹣x
B 340﹣x x﹣40
故答案为:400﹣x;340﹣x;x﹣40;
(2)由题意可得,
W=20x+25(400﹣x)+15(340﹣x)+24(x﹣40)=4x+14140,
∵340﹣x≥0且x﹣40≥0,
∴40≤x≤340,
即W(元)与x(吨)的函数关系式是W=4x+14140(40≤x≤340);
(3)∵y=4x+14140,k=4>0,
∴y随x的增大而增大,
∵40≤x≤340,
∴当x=40时,y取得最小值,此时y=14300,400﹣x=360,340﹣x=300,x﹣40=0,
答:从A城运往C乡40吨,运往D乡360吨;从B城运往C乡300吨,运往D乡0吨,此时总运费最少,总运费最小值是14300元.
【变式2-1】(2021 寻乌县模拟)疫情期间,甲、乙两个仓库要向M,N两地运送防疫物资,已知甲仓库可调出50吨防疫物资,乙仓库可调出40吨防疫物资,M地需35吨防疫物资,N地需55吨防疫物资,两仓库到M,N两地的路程和运费如下表:
路程/千米 运送1千米所需运费/(元/吨)
甲仓库 乙仓库 甲仓库 乙仓库
M地 20 15 12 12
N地 25 20 10 8
(1)设从甲仓库运往M地防疫物资x吨,两仓库运往M,N两地的总费用为y元,求y关于x的函数关系式.
(2)如何调运才能使总运费最少?总运费最少是多少?
【解题思路】(1)设甲仓库运往M地的防疫物资为x吨,甲仓库运往N地的防疫物资为(50﹣x)吨,乙仓库运往M地的防疫物资为(35﹣x)吨,乙仓库运往N地的防疫物资为(5+x)吨,根据题意列出函数解析式,并求出自变量的取值范围;
(2)根据一次函数的性质以及自变量的取值范围求出函数最小值.
【解答过程】解:设甲仓库运往M地的防疫物资为x吨,甲仓库运往N地的防疫物资为(50﹣x)吨,
乙仓库运往M地的防疫物资为(35﹣x)吨,乙仓库运往N地的防疫物资为(5+x)吨,
根据题意得:y=12×20x+10×25(50﹣x)+12×15×(35﹣x)+8×20(5+x)
=﹣30x+19600,
∵x≥0,50﹣x≥0,35﹣x≥0,
∴0≤x≤35,
∴y关于x的函数关系式为y=﹣30x+19600(0≤x≤35);
(2)∵y=﹣30x+19600,﹣30<0,
∴y随x的增大而减小,
∵0≤x≤35,
∴当x=35时,总运费最少,
即从甲仓库运往M地35吨,
甲仓库运往N地:50﹣35=15(吨),
乙仓库运往M地:55﹣15=40(吨),
乙仓库运往N地:40﹣40=0(吨),
∴总运费最少为:﹣30×35+19600=18550(元).
∴从甲仓库运往M地35吨,运往N地15吨;从乙仓库运往N地40吨时总运费最少,总运费最少是18550元.
【变式2-2】(2021春 满洲里市期末)已知A地有蔬菜200t,B地有蔬菜300t,现决定将这些蔬菜全部调运给C,D两地,C,D两地分别需要调运蔬菜240t和260t.其中从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C地的蔬菜为x吨.设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案.
【解题思路】根据从B地运往C地的蔬菜为x吨,可以用含x的式子表示出运往各地的吨数,然后即可写出w与x的函数关系式,再根据一次函数的性质和x的取值范围,即可得到总运费最小的调运方案,
【解答过程】解:设从B地运往C地的蔬菜为x吨,则从B地运往D地的蔬菜为(300﹣x)吨,从A地运往C地的蔬菜为(240﹣x)吨,从A地运往D地的蔬菜为(x﹣40)吨.
w=20(240﹣x)+25(x﹣40)+15x+18(300﹣x)=2x+9200,
由题意得,,
解得40≤x≤240,
∵w=2x+9200,k=2>0,
∴w随x的增大而增大,
∴当x=40时,总运费w有最小值9280元,240﹣x=200,x﹣40=0,300﹣x=260,
答:w与x之间的函数关系式是w=2x+9200,总运费最小的调运方案是从A地运往C地200吨,B地运往C地40吨,B地运往D地260吨.
【变式2-3】(2021春 昆明期末)某市A、B两个仓库分别有救灾物资200吨和300吨,2021年5月18日起云南大理州漾濞县已连续发生多次地震,最高震级为5月21日发生的6.4级地震,为援助灾区,现需将这些物资全部运往甲,乙两个受灾村.已知甲村需救灾物资240吨,乙村需救灾物资260吨,从A仓库运往甲,乙两村的费用分别为每吨20元和每吨25元,从B仓库运往甲,乙两村的费用分别为每吨15元和24元.设A仓库运往甲村救灾物资x吨,请解答下列问题:
(1)根据题意,填写下表格:
仓库 甲村 乙村
A x ①
B ② ③
①= 200﹣x ;②= 240﹣x ;③= x+60 .
(2)设总运费为W(元),求出W(元)与x(吨)的函数关系式.
(3)求怎么调运可使总运费最少?最少运费为多少元?
【解题思路】(1)根据题意用含x的代数式表示即可;
(2)根据题意直接列式:y=20x+25(200﹣x)+15(240﹣x)+24(x+60)化简即可;
(3)由(2)中的一次函数可知,y随x的减小而减小,要使总运费最低,x必须取最小值,计算各个运货数量设计方案即可.
【解答过程】解:(1)∵A、B两个仓库分别有救灾物资200吨和300吨,甲村需救灾物资240吨,乙村需救灾物资260吨,
∴设A仓库运往甲村救灾物资x吨,则运往乙村(200﹣x)吨,B仓库运往甲村(240﹣x)吨,运往乙村[300﹣(240﹣x)]=(x+60)吨,
∴①=200﹣x,②=240﹣x,③=x+60.
故答案为:200﹣x,240﹣x,x+60.
(2)W=20x+25(200﹣x)+15(240﹣x)+24(x+60)=4x+10040(0≤x≤200).
(3)∵一次函数W=4x+10040,k=4>0,
∴y随x的减小而减小,
∴要使总运费最低,x必须取最小值.
∴当x=6时,总运费最少是10040元.
调运方案为:从A村运往乙库200吨,从B村运往甲库240吨,运往乙库60吨.
【题型3 一次函数的应用(利润最大化)】
【例3】(2021 镇雄县二模)2020年6月1日上午,国务院总理在山东烟台考察时表示,地摊经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机.“地摊经济”成为了社会关注的热门话题.小明从市场得知如表信息:
甲商品 乙商品
进价(元/件) 35 5
售价(元/件) 45 8
小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
(1)求出y与x之间的函数关系式;
(2)小明用不超过2000元资金一次性购进甲,乙两种商品,求x的取值范围;
(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于632.5元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大.
【解题思路】(1)由y=甲商品利润+乙商品利润,可得解析式;
(2)由用不超过2000元资金一次性购进甲,乙两种商品,列出不等式组,即可求解;
(3)由获得的利润不少于632.5元,列出不等式可求x的范围,由一次函数的性质可求解.
【解答过程】解:(1)由题意可得:y=(45﹣35)x+(8﹣5)(100﹣x)=7x+300;
(2)由题意可得:35x+5(100﹣x)≤2000,
∴x≤50,
又∵x≥0,
∴0≤x≤50,且x为整数;
(3)由题意可得:(45﹣35)x+(8﹣5)(100﹣x)≥632.5,
∴x≥47.5,
∴47.5≤x≤50,
又∵x为整数,
∴x=48,49,50,
∴进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件;
∵y=7x+300,
∴y随x的增大而增大,
∴当x=50时,有最大利润.
∴当甲商品进50件,乙商品进50件,利润有最大值.
【变式3-1】(2021 青白江区模拟)在近期“抗疫”期间,某药店销售A,B两种型号的口罩,已知销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍,则该药店购进A型、B型口罩各多少只,才能使销售总利润y最大?
【解题思路】(1)设每只A型口罩销售利润为a元,每只B型口罩销售利润为b元,根据“销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为180元”列方程组解答即可;
(2)根据题意即可得出y关于x的函数关系式;根据题意列不等式得出x的取值范围,再结合y关于x的函数关系式解答即可.
【解答过程】解:(1)设每只A型口罩销售利润为a元,每只B型口罩销售利润为b元,根据题意得:
,
解得,
答:每只A型口罩销售利润为0.15元,每只B型口罩销售利润为0.2元;
(2)根据题意得,y=0.15x+0.2(2000﹣x),即y=﹣0.05x+400;
根据题意得,,
解得500≤x≤1000,
∴y=﹣0.05x+400(500≤x≤1000),
∵﹣0.05<0,
∴y随x的增大而减小,
∵x为正整数,
∴当x=500时,y取最大值,则2000﹣x=1500,
即药店购进A型口罩500只、B型口罩1500只,才能使销售总利润最大.
【变式3-2】(2021春 连山区期末)由于新能源汽车越来越受到消费者的青睐,某经销商决定分两次购进甲、乙两种型号的新能源汽车(两次购进同一种型号汽车的每辆的进价相同).第一次用270万元购进甲型号汽车30辆和乙型号汽车20辆;第二次用128万元购进甲型号汽车14辆和乙型号汽车10辆.
(1)求甲、乙两种型号汽车每辆的进价;
(2)经销商分别以每辆甲型号汽车8.8万元,每辆乙型号汽车4.2万元的价格销售后,根据销售情况,决定再次购进甲、乙两种型号的汽车共100辆,且乙型号汽车的数量不少于甲型号汽车数量的3倍,设再次购进甲型汽车a辆,这100辆汽车的总销售利润为W万元.
①求W关于a的函数关系式;并写出自变量的取值范围;
②若每辆汽车的售价和进价均不变,该如何购进这两种汽车,才能使销售利润最大?最大利润是多少?
【解题思路】(1)设甲种型号汽车的进价为a万元、乙种型号汽车的进价为b万元,根据“第一次用270万元购进甲型号汽车30辆和乙型号汽车20辆;第二次用128万元购进甲型号汽车14辆和乙型号汽车10辆”得到相应的二元一次方程组,解方程组即可得到甲、乙两种型号汽车每辆的进价;
(2)①根据题意可以得到利润与购买甲种型号汽车数量的函数关系;
②根据乙型号汽车的数量不少于甲型号汽车数量的3倍,可以得到购买甲种型号汽车数量的取值范围,然后根据一次函数的性质,即可得到最大利润和此时的购买方案.
【解答过程】解:(1)设甲种型号汽车的进价为a万元、乙种型号汽车的进价为b万元,,
解得:,
答:甲、乙两种型号汽车每辆的进价分别为7万元、3万元;
(2)①由题意得:购进乙型号的汽车(100﹣a)辆,
则W=(8.8﹣7)a+(4.2﹣3)×(100﹣a)=0.6a+120,
乙型号汽车的数量不少于甲型号汽车数量的3倍,
∴100﹣a≥3a,且a≥0,
解得,0≤a≤25,
∴W关于a的函数关系式为W=0.6a+120(0≤a≤25);
②W=0.6a+120,
∵0.6>0,
∴W随着a的增大而增大,
∵0≤a≤25,
∴当a=25时,W取得最大值,此时W=0.6×25+120=135(万元),
100﹣25=75(辆),
答:获利最大的购买方案是购进甲型汽车25辆,乙型汽车75辆,最大利润是135万元.
【变式3-3】(2021 鹿邑县一模)草莓是一种极具营养价值的水果,当下正是草莓的销售旺季.某水果店以2850元购进两种不同品种的盒装草莓.若按标价出售可获毛利润1500元(毛利润=售价﹣进价),这两种盒装草莓的进价、标价如表所示:
价格/品种 A品种 B品种
进价(元/盒) 45 60
标价(元/盒) 70 90
(1)求这两个品种的草莓各购进多少盒;
(2)该店计划下周购进这两种品种的草莓共100盒(每种品种至少进1盒),并在两天内将所进草莓全部销售完毕(损耗忽略不计).因B品种草莓的销售情况较好,水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒.如何安排进货,才能使毛利润最大,最大毛利润是多少?
【解题思路】(1)根据某水果店以2850元购进两种不同品种的盒装草莓,按标价出售可获毛利润1500元和表格中的数据,可以列出相应的二元一次方程组,然后求解即可;
(2)根据题意,可以写出毛利润和购买A种草莓数量的函数关系式,然后根据水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒,可以得到相应的不等式,求出A种草莓数量的取值范围,再根据一次函数的性质,即可得到如何安排进货,才能使毛利润最大,最大毛利润是多少.
【解答过程】解:(1)设A品种的草莓购进x盒,B品种的草莓购进y盒,
由题意可得,,
解得,
答:A品种的草莓购进30盒,B品种的草莓购进25盒;
(2)设A品种的草莓购进a盒,则B品种的草莓购进(100﹣a)盒,毛利润为w元,
由题意可得,w=(70﹣45)a+(90﹣60)×(100﹣a)=﹣5a+3000,
∵k=﹣5<0,
∴w随a的增大而减小,
∵水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒,
∴,
解得20≤a≤33,
∴当a=20时,w取得最大值,此时w=﹣5×20+3000=2900,100﹣a=80,
答:当A品种的草莓购进20盒,B品种的草莓购进80盒时,才能使毛利润最大,最大毛利润是2900元.
【题型4 一次函数的应用(费用最低)】
【例4】(2021春 广安期末)为积极响应垃圾分类的号召,某街道决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱.已知购买3个垃圾箱和2个温馨提示牌需要280元,购买2个垃圾箱和3个温馨提示牌需要270元.
(1)每个垃圾箱和每个温馨提示牌各多少元?
(2)若购买垃圾箱和温馨提示牌共100个(两种都买),且垃圾箱的个数不少于温馨提示牌个数的3倍,请写出总费用w(元)与垃圾箱个数m(个)之间的函数关系式,并说明当购买垃圾箱和温馨提示牌各多少个时,总费用最低,最低费用为多少元?
【解题思路】(1)根据购买3个垃圾箱和2个温馨提示牌需要280元,购买2个垃圾箱和3个温馨提示牌需要270元,可以列出相应的二元一次方程组,然后求解即可;
(2)根据题意,可以写出w与m的函数关系式,然后根据垃圾箱的个数不少于温馨提示牌个数的3倍,即可得到m的取值范围,然后根据一次函数的性质,即可得到当购买垃圾箱和温馨提示牌各多少个时,总费用最低,最低费用为多少元.
【解答过程】解:(1)设每个垃圾箱和每个温馨提示牌分别为x元、y元,
由题意可得,,
解得,
答:每个垃圾箱和每个温馨提示牌分别为60元、50元;
(2)设购买垃圾箱m个,则购买温馨提示牌(100﹣m)个,
w=60m+50(100﹣m)=10m+5000,
∵垃圾箱的个数不少于温馨提示牌个数的3倍,
∴m≥3(100﹣m),
解得m≥75,
∴当m=75时,w取得最小值,此时w=5750,100﹣m=25,
答:总费用w(元)与垃圾箱个数m(个)之间的函数关系式是w=10m+5000,当购买垃圾箱和温馨提示牌分别为75个、25个时,总费用最低,最低费用为5750元.
【变式4-1】(2021春 环江县期末)某县园林局打算购买三角梅、水仙装点城区道路,负责人小李去花卉基地调查发现:购买1盆三角梅和2盆水仙需要14元,购买2盆三角梅和1盆水仙需要13元.
(1)求三角梅、水仙的单价各是多少元?
(2)购买三角梅、水仙共10000盆,且购买的三角梅不少于3000盆,但不多于5000盆.
①设购买的三角梅种花a盆,总费用为W元,求W与a的关系式;
②当总费用最少时,应选择哪一种购买方案?最少费用为多少元?
【解题思路】(1)根据购买1盆三角梅和2盆水仙需要14元,购买2盆三角梅和1盆水仙需要13元,可以列出相应的二元一次方程组,解方程组即可得到三角梅、水仙的单价各为多少元;
(2)①根据题意,可以写出W与m的关系式;
②根据①中的函数关系式和一次函数的性质,即可得到使总花费最少的够花方案,并求出最少费用.
【解答过程】解:(1)设三角梅、水仙的单价分别为x元、y元,
根据题意得,
解得,
答:三角梅、水仙的的单价分别为4元、5元;
(2)①由题意可得,W=4a+5(10000﹣a),
即W与a的关系式是W=﹣a+50000(3000≤a≤5000);
②∵W=﹣a+50000,
∴W随a的增大而减小,
∵3000≤a≤5000,
∴当a=5000时,W取得最小值,
此时W=45000,10000﹣a=1000﹣5000=5000,
答:当购买三角梅、水仙各5000盆时,总花费最少,最少费用为45000元.
【变式4-2】(2021 三水区校级二模)截至2021年4月10日,全国累计报告接种新冠疫苗16447.1万剂次,接种总剂次数为全球第二.某社区有80000人每人准备接种两剂次相同厂家生产的新冠疫苗并被分配到A、B两个接种点,A接种点有5个接种窗口,B接种点有4个接种窗口.每个接种窗口每天的接种量相同,并且在独立完成20000人的两剂次新冠疫苗接种时,A接种点比B接种点少用5天.
(1)求A、B两个接种点每天接种量;
(2)设A接种点工作x天,B接种点工作y天,刚好完成该社区80000人的新冠疫苗接种任务,求y关于x的函数关系式;
(3)在(2)的条件下,若A接种点每天耗费6.5万元,B接种点每天耗费为4万元,且A、B两个接种点的工作总天数不超过85天,则如何安排A、B两个接种点工作的天数,使总耗费最低?并求出最低费用.
【解题思路】(1)设A接种点每天接种量为5x剂次,B接种点每天接种量为4x剂次,由题意:在独立完成20000人的两剂次新冠疫苗接种时,A接种点比B接种点少用5天.列出分式方程,解方程即可;
(2)结合(1)的结论即可得出y关于x的函数关系式;
(3)根据“A、B两个接种点的工作总天数不超过85天”可得x+y≤85,再把(2)的结论代入可得关于x的不等式,解不等式求出x的取值范围;设总耗费为w万元,由题意求出w与x的函数关系式,再根据一次函数的性质解答即可.
【解答过程】解:(1)设A接种点每天接种量为5x剂次,B接种点每天接种量为4x剂次,
由题意得:,
解得:x=400,
经检验,x=400是原方程的解,且符合题意,
则4x=1600,5x=2000,
答:设A接种点每天接种量为2000剂次,B接种点每天接种量为1600剂次;
(2)由(1)得2000x+1600y=80000×2,
∴y100;
(3)由题意,得x+y≤85,
即x+(100)≤85,
解得x≥60,
设总耗费为w万元,
则w=6.5x+4(100)=1.5x+400.
∵1.5>0,
∴w随x的增大而增大,
∴当x=60时,w取值最小,最小值为:1.5×60+400=490(万元),
∴y25,
答:安排A接种点工作60天,B种接种点工作25天,使总耗费最低,最低费用为490万元.
【变式4-3】(2021春 大同期末)在新冠疫情防控期间,某校新购进A、B两种型号的电子体温测量仪共20台,其中A型仪器的数量不少于B型仪器的,已知A、B两种测温仪的价格如表所示,请问购买A、B两种测温仪各多少台时,可使所购仪器的总费用最少?最少需多少元?
型号 A B
价格 800元/台 600元/台
【解题思路】根据题意和表格中的数据,可以写出费用与A种型号测温仪台数的函数关系式,然后根据某校新购进A、B两种型号的电子体温测量仪共20台,A型仪器的数量不少于B型仪器的,可以得到A种型号台数的取值范围,再根据一次函数的性质,即可得到购买A、B两种测温仪各多少台时,可使所购仪器的总费用最少,最少需多少元.
【解答过程】解:设购买A种型号的测温仪x台,则购买B种型号的测温仪(20﹣x)台,所需费用为w元,
由题意可得,w=800x+600(20﹣x)=200x+12000,
∴w随x的增大而增大,
∵某校新购进A、B两种型号的电子体温测量仪共20台,A型仪器的数量不少于B型仪器的,
∴(20﹣x)≤x≤20,
解得8≤x≤20,
∴当x=8时,w取得最小值,此时w=200×8+12000=13600,20﹣x=12,
答:购买A、B两种测温仪分别为8台、12台时,可使所购仪器的总费用最少,最少需13600元.
【题型5 一次函数的应用(工程问题)】
【例5】(2021 汇川区三模)为了主题为“醉美遵义,酒都仁怀”第十三届遵义文化旅游产业发展大会召开,仁怀某社区计划对面积为2000m2的区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2.5倍,并且在独立完成面积为500m2区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数解析式.
(3)若甲队每天绿化费用是1.5万元,乙队每天绿化费用为0.5万元,且甲乙两队施工的总天数不超过19天,则如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低费用.
【解题思路】(1)设乙工程队每天能完成绿化的面积是xm2,则乙甲队每天能完成绿化面积2.5xm2,根据在独立完成面积为500m2区域的绿化时,甲队比乙队少用6天,列方程求解;
(2)根据(1)的结论即可求出y与x的函数解析式.
(3)根据甲乙两队施工的总天数不超过19天,得到x的取值范围,设施工总费用为w元,根据题意得出w与x的函数关系式,根据一次函数的性质,即可解答.
【解答过程】解:(1)设乙工程队每天能完成绿化的面积是xm2,则乙甲队每天能完成绿化面积2.5xm2,
根据题意得:,
解得x=50,
经检验,x=50是原方程的解并满足题意,
则甲工程队每天能完成绿化的面积是:50×2.5=125(m2),
答:甲、乙两工程队每天能完成绿化的面积分别是125m2、50m2;
(2)根据题意,得:125x+50y=2000,
整理得:y=40﹣2.5x,
∴y与x的函数解析式为:y=40﹣2.5x;
(3)∵甲乙两队施工的总天数不超过19天,
∴x+y≤19,
∴x+40﹣2.5x≤19,
解得:x≥14,
设施工总费用为w元,根据题意得:
w=1.5x+0.5y=1.5x+0.5×(40﹣2.5x)=0.25x+20,
∵k=0.25>0,
∴w随x减小而减小,
∴当x=14时,w有最小值,最小值为0.25×14+20=23.5(万元),
此时y=19﹣14=5.
答:安排甲队施工14天,乙队施工5天时,施工总费用最低为23.5万元.
【变式5-1】(2021春 青羊区期末)甲、乙两个工程队分别同时铺设两条公路,所铺设公路的长度y(m)与铺设时间x(h)之间的关系如图所示,根据图象所提供的信息分析,解决下列问题:
(1)在2时~6时段时,乙队的工作效率为 5 m/h;
(2)分别求出乙队在0时~2时段和2时~6时段,y与x的关系式,并求出甲乙两队所铺设公路长度相等时x的值;
(3)求出当两队所铺设的公路长度之差为5m时x的值.
【解题思路】(1)根据图象即可求出在2时~6时段时,乙队的工作效率;
(2)根据图中的信息利用待定系数法即可确定函数关系式;再根据函数关系式列方程解答即可;
(3)利用(2)中的函数关系式可以解决问题.
【解答过程】解:(1)在2时~6时段时,乙队的工作效率为:(50﹣30)÷(6﹣2)=5(m/h),
故答案为:5;
(2)当0≤x≤2时,设乙队y与x的函数解析式为y=kx,可得2k=30,解得k=15,即y=15x;
当2≤x≤6时,设y与x的函数解析式为y=nx+m,
可得,
解得,
即y=5x+20,
∴;
10x=5x+20,解得x=4,
即甲乙两队所挖河渠长度相等时x的值为4;
(3)当0≤x≤2时,15x﹣10x=5,解得x=1.
当2<x≤4时,5x+20﹣10x=5,解得x=3,
当4<x≤6时,10x﹣(5x+20)=5,解得x=5.
答:当两队所挖的河渠长度之差为5m时,x的值为1h或3h或5h.
【变式5-2】(2021春 沙坪坝区校级期末)甲、乙两人同时开始共同组装一批零件,工作两小时后,乙因事离开,停止工作.一段时间后,乙重新回到岗位并提高了工作效率.最后40分钟,甲休息,由乙独自完成剩余零件的组装.甲在工作过程中工作效率保持不变,乙在每个工作阶段的工作效率保持不变.甲、乙两人组装零件的总数y(个)与工作时间x(小时)之间的图象如图.
(1)这批零件一共有多少个?
(2)在整个组装过程中,当甲、乙各自组装的零件总数相差40个时,求x的值.
【解题思路】(1)根据题意和函数图象中的数据,可以分别计算出甲的速度、乙开始和后来的速度,然后即可计算出这批零件一共有多少个;
(2)根据(1)中的结果和分类讨论的方法,可以求得x的值.
【解答过程】解:(1)由图象可得,
甲的工作效率是:(690﹣420)÷(5﹣2)=90(个/小时),
乙刚开始的工作效率是:420÷2﹣90=120(个/小时),
乙后来的工作效率是:(1320﹣690)÷(85)﹣90=180(个/小时),
1320+180
=1320+120
=1440(个),
答:这批零件一共有1440个;
(2)当0≤x<2时,
(120﹣90)x=40,
解得x;
当2≤x<5时,
120×2﹣90x=40或90x﹣120×2=40,
解得x=2或x=3;
当5≤x<8时,
90x﹣120×2﹣180(x﹣5)=40或120×2+180(x﹣5)﹣90x=40,
解得x=6或x=7(舍去);
当8x≤8时,
120×2+180(x﹣5)﹣90×(8)=40,
解得x=7;
由上可得,在整个组装过程中,当甲、乙各自组装的零件总数相差40个时,x的值是,2,3,6或7.
【变式5-3】(2020秋 郑州期末)工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间t(时),甲组加工零件的数量为y甲(个),乙组加工零件的数量为y乙(个),其函数图象如图所示.
(1)求y乙与t之间的函数关系式,并写出t的取值范围;
(2)求a的值,并说明a的实际意义;
(3)甲组加工多长时间时,甲、乙两组加工零件的总数为480个.
【解题思路】(1)根据函数图象中的数据,可以得到y乙与t之间的函数关系式,并写出t的取值范围;
(2)根据函数图象中的数据,可以得到甲的速度,然后即可计算出a的值,然后再说明a的实际意义即可;
(3)根据题意,可以列出相应的方程,然后即可得到甲组加工多长时间时,甲、乙两组加工零件的总数为480个.
【解答过程】解:(1)设y乙与t之间的函数关系式是y乙=kt+b,
,
解得,
即y乙与t之间的函数关系式是y乙=120t﹣600(5≤t≤8);
(2)由图象可得,
甲的工作效率为120÷3=40(个/时),
a=120+40×(8﹣4)=280,
即a的值是280,实际意义是当甲加工8小时时,一共加工了280个零件;
(3)设甲组加工c小时时,甲、乙两组加工零件的总数为480个,
120+40(c﹣4)+(120c﹣600)=480,
解得c=7,
即甲组加工7小时时,甲、乙两组加工零件的总数为480个.
【题型6 一次函数的应用(其他问题)】
【例6】(2021春 沙河口区期末)为预防疫情传播,学校对教室定期喷药消毒.如图为一次消毒中,某教室每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)的函数图象,它是由关闭门窗集中喷药,通风前和打开门窗后通风三段不同的一次函数组成的.在下面四个选项中,错误的是( )
A.经过5min集中喷药,教室每立方米空气中含药量最高达到10mg/m3
B.持续11min室内空气中的含药量不低于8mg/m3
C.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才有效杀灭病毒.由此判断此次消毒有效
D.当室内空气中的含药量低于4mg/m3时,对人体是安全的.从室内空气中的含药量达到10mg/m3开始,需经过40min后学生才能进入室内
【解题思路】根据图象分别求出三段一次函数的解析式即可判断.
【解答过程】解:设三段一次函数的解析式为:y=k1x,y=k2x+b1,y=k3x+b2,
由图象可得,10=5k1,,,
解得k1=2,,,
∴三段函数的解析式为:y=2x,yx+11,yx,
A通过图象可得,经过5min集中喷药,教室每立方米空气中含药量最高达到10mg/m3,故A正确;
B将y=8代入y=2x得x=4,15﹣4=11,因此持续11min室内空气中的含药量不低于8mg/m3,故B正确;
C将y=5代入y=2x得x,将y=5代入yx得x=45,4542.5>35,由此判断此次消毒有效,故C正确;
D将y=4代入yx得x=55,55﹣5=50,由此从室内空气中的含药量达到10mg/m3开始,需经过50min后学生才能进入室内,故D错误;
故选:D.
【变式6-1】(2021春 朝阳区校级期末)某地自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.
(1)某月该单位用水3200吨,水费是 1660 元;若用水2800吨,水费是 1400 元;
(2)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式;
(3)若某月该单位缴纳水费1540元,则该单位这个月的用水量为多少吨?
【解题思路】(1)由2800≤3000,根据“水费=每吨水费×用水量”即可算出此时水费;由3200>3000,根据“水费=3000×0.5+超出部分×0.8”即可算出此时水费;
(2)分0≤x≤3000以及x>3000来考虑,根据“水费=每吨水费×用水量和水费=3000×0.5+超出部分×0.8”即可得出y关于x的函数解析式;
(3)根据用水3000吨的收费可知该单位本月用水量超过3000吨,故把1540代入y=0.8x﹣900求出x即可.
【解答过程】解:(1)某月该单位用水3200吨,水费是:3000×0.5+(3200﹣3000)×0.8=1660(元);
若用水2800吨,水费是:2800×0.5=1400(元).
故答案为:1660,1400;
(2)根据题意,当0≤x≤3000时,y=0.5x;
当x>3000时,y=0.5×3000+0.8×(x﹣3000)=0.8x﹣900,
所以y关于x的函数解析式为:y;
(3)如果该单位一个月用水3000吨,则应交水费:0.5×3000=1500(元),
∵1540>1500,
∴该单位某月用水超过3000吨,
∴把y=1540代入y=0.8x﹣900得:
0.8x﹣900=1540,
解得:x=3050,
∴该单位这个月的用水量为3050吨.
【变式6-2】(2021春 河东区期末)一个水库的水位在某段时间内持续上涨,表格中记录了连续5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
0 1 2 3 4 5
3 3.3 3.6 3.9 4.2 4.5
(1)水位高度y是否为时间x的函数?若是,请求出这个函数解析式;
(2)据估计,这种上涨规律还会持续,并且当水位高度达到8m时,水库报警系统会自动发出警报.请预测再过多久系统会发出警报?
【解题思路】(1)根据题意和表格中的数据可以求得y与x之间的函数解析式;
(2)将y=8代入(1)中的函数解析式,求出x的值,再用x的值减去5即可解答本题.
【解答过程】解:(1)设y与x之间的函数解析式为y=kx+b,
,
解得,
即y与x之间的函数解析式为y=0.3x+3;
(2)把y=8,代入y=0.3x+3,得
8=0.3x+3,
解得,x,
,
答:再过小时后系统会发出警报.
【变式6-3】(2021 涧西区三模)某大型商场为了提高销售人员的积极性,对原有的薪酬计算方式进行了修改,设销售人员一个月的销售量为x(件),销售人员的月收入为y(元),原有的薪酬计算方式y1元采用的是底薪+提成的方式,且y1=k1x+b,已知每销售一件商品另外获得15元的提成修改后的薪酬计算方式为y2(元),且y2=k2x+b,根据图象回答下列问题:
(1)求y1和y2的解析式,并说明b的实际意义;
(2)求两个函数图象的交点F的坐标,并说明交点F的实际意义;
(3)根据函数图象请判断哪种薪酬计算方式更适合销售人员.
【解题思路】(1)根据函数图象中的数据可以求得y1和y2的函数关系式;
(2)联立方程组,解方程组可得点F的坐标,根据题目条件可得F的实际意义;
(3)根据(1)中的函数解析式和(2)中点F的坐标,即可解答本题.
【解答过程】解:(1)∵y1=k1x+b的图象过点(0,3000),
∴b=3000,
又∵每销售一件商品另外获得15元的提成,
∴k1=15,
∴y1=15x+3000,
∵y2=k2x+b的图象过点(100,3000),由图象可得b=0,
∴100k2=3000,
解得k2=30,
∴y2=30x,
∴y1中b的实际意义为底薪为3000元,y2中b的实际意义为底薪为0元;
(2),
解得.
∴F(200,6000),
∴F点的实际意义是当销售200件商品时,两种薪酬计算方式所得薪酬相等为6000元;
(3)结合函数图象可知,当0<x<200时,原有的薪酬计算方式更适合销售人员,
当x=200时,选择两种薪酬计算方式对销售人员一样.
当x>200时,修改后的薪酬计算方式更适合销售人员.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
一次函数的应用6大题型
【知识点1 一次函数与实际问题】
在研究有关一次函数的实际问题时,要遵循一审、二设、三列、四解的方法:
第1步:审题。认真读题,分析题中各个量之间的关系;
第2步:设自变量。根据各个量之间的关系设满足题意的自变量;
第3步:列函数。根据各个量之间的关系列出函数;
第4步:求解。求出满足题意的数值。
【题型1 一次函数的应用(行程问题)】
【例1】(2021春 海门市期中)甲、乙两人分别从笔直道路上的A、B两地同时出发相向匀速而行,已知甲比乙先出发6分钟,两人在C地相遇,相遇后甲立即按原速原路返回A地,乙继续向A地前行,约定先到A地者停止运动就地休息.若甲、乙两人相距的路程y(米)与甲行走的时间x(分钟)之间的关系如图所示,有下列说法:①甲的速度是60米/分钟,乙的速度是80米/分钟;②甲出发30分钟时,两人在C地相遇;③乙到达A地时,甲与A地相距450米,其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
【变式1-1】(2021春 巴彦淖尔期末)如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,判断下列结论正确的选项是( )
①汽车在行驶途中停留了0.5h;
②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;
④汽车出发4h离出发地40km.
A.①②④ B.①②③ C.①③④ D.①②③④
【变式1-2】(2021 沙坪坝区校级开学)某天上午,大学生小南从学校出发去重庆市图书馆查阅资料,同时他的同学小开从该图书馆看完书回学校.两人在途中相遇,于是马上就各自最近的研究课题交流了6分钟,又各自按原速前往自己的目的地.直到小开回到学校并电话告知小南后,小南决定提速25%到达图书馆(接打电话的时间忽略不计).在整个运动过程中,小南和小开之间的距离y(m)与小南所用的时间x(min)之间的函数关系如图所示,则下列说法中正确的是( )
A.学校和图书馆的之间的距离为1200m
B.小南提速前,小开的速度是小南的1.8倍
C.m=1500
D.n=62
【变式1-3】(2021 蒙阴县二模)甲、乙两车从M地到480千米的N地,甲车比乙车晚出发2小时,乙车途中因故停车检修,图中线段DE、折线OABC分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数图象,请根据图象所提供的信息,解决如下问题:
(1)求两车在途中第二次相遇时,它们距目的地的路程;
(2)甲车出发多长时间,两车在途中第一次相遇?
【题型2 一次函数的应用(调运问题)】
【例2】(2021春 大安市期末)A城有肥料400吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡镇,从A城运往C、D两乡镇肥料费为20元/吨和25元/吨;从B城往C、D两乡镇运肥料的费用分别为15元/吨和24元/吨,C乡镇需要肥料340吨,D乡镇需要肥料360吨.设A城运往C乡镇x吨肥料,请解答下列问题:
(1)根据题意,填写下列表格:
城、乡/吨数 C D
A x
B
(2)设总运费为W(元),求出W(元)与x(吨)的函数关系式,并写出自变量的取值范围;
(3)求怎样调运可使总运费最少?最少为多少元?
【变式2-1】(2021 寻乌县模拟)疫情期间,甲、乙两个仓库要向M,N两地运送防疫物资,已知甲仓库可调出50吨防疫物资,乙仓库可调出40吨防疫物资,M地需35吨防疫物资,N地需55吨防疫物资,两仓库到M,N两地的路程和运费如下表:
路程/千米 运送1千米所需运费/(元/吨)
甲仓库 乙仓库 甲仓库 乙仓库
M地 20 15 12 12
N地 25 20 10 8
(1)设从甲仓库运往M地防疫物资x吨,两仓库运往M,N两地的总费用为y元,求y关于x的函数关系式.
(2)如何调运才能使总运费最少?总运费最少是多少?
【变式2-2】(2021春 满洲里市期末)已知A地有蔬菜200t,B地有蔬菜300t,现决定将这些蔬菜全部调运给C,D两地,C,D两地分别需要调运蔬菜240t和260t.其中从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C地的蔬菜为x吨.设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案.
【变式2-3】(2021春 昆明期末)某市A、B两个仓库分别有救灾物资200吨和300吨,2021年5月18日起云南大理州漾濞县已连续发生多次地震,最高震级为5月21日发生的6.4级地震,为援助灾区,现需将这些物资全部运往甲,乙两个受灾村.已知甲村需救灾物资240吨,乙村需救灾物资260吨,从A仓库运往甲,乙两村的费用分别为每吨20元和每吨25元,从B仓库运往甲,乙两村的费用分别为每吨15元和24元.设A仓库运往甲村救灾物资x吨,请解答下列问题:
(1)根据题意,填写下表格:
仓库 甲村 乙村
A x ①
B ② ③
①= ;②= ;③= .
(2)设总运费为W(元),求出W(元)与x(吨)的函数关系式.
(3)求怎么调运可使总运费最少?最少运费为多少元?
【题型3 一次函数的应用(利润最大化)】
【例3】(2021 镇雄县二模)2020年6月1日上午,国务院总理在山东烟台考察时表示,地摊经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机.“地摊经济”成为了社会关注的热门话题.小明从市场得知如表信息:
甲商品 乙商品
进价(元/件) 35 5
售价(元/件) 45 8
小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
(1)求出y与x之间的函数关系式;
(2)小明用不超过2000元资金一次性购进甲,乙两种商品,求x的取值范围;
(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于632.5元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大.
【变式3-1】(2021 青白江区模拟)在近期“抗疫”期间,某药店销售A,B两种型号的口罩,已知销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍,则该药店购进A型、B型口罩各多少只,才能使销售总利润y最大?
【变式3-2】(2021春 连山区期末)由于新能源汽车越来越受到消费者的青睐,某经销商决定分两次购进甲、乙两种型号的新能源汽车(两次购进同一种型号汽车的每辆的进价相同).第一次用270万元购进甲型号汽车30辆和乙型号汽车20辆;第二次用128万元购进甲型号汽车14辆和乙型号汽车10辆.
(1)求甲、乙两种型号汽车每辆的进价;
(2)经销商分别以每辆甲型号汽车8.8万元,每辆乙型号汽车4.2万元的价格销售后,根据销售情况,决定再次购进甲、乙两种型号的汽车共100辆,且乙型号汽车的数量不少于甲型号汽车数量的3倍,设再次购进甲型汽车a辆,这100辆汽车的总销售利润为W万元.
①求W关于a的函数关系式;并写出自变量的取值范围;
②若每辆汽车的售价和进价均不变,该如何购进这两种汽车,才能使销售利润最大?最大利润是多少?
【变式3-3】(2021 鹿邑县一模)草莓是一种极具营养价值的水果,当下正是草莓的销售旺季.某水果店以2850元购进两种不同品种的盒装草莓.若按标价出售可获毛利润1500元(毛利润=售价﹣进价),这两种盒装草莓的进价、标价如表所示:
价格/品种 A品种 B品种
进价(元/盒) 45 60
标价(元/盒) 70 90
(1)求这两个品种的草莓各购进多少盒;
(2)该店计划下周购进这两种品种的草莓共100盒(每种品种至少进1盒),并在两天内将所进草莓全部销售完毕(损耗忽略不计).因B品种草莓的销售情况较好,水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒.如何安排进货,才能使毛利润最大,最大毛利润是多少?
【题型4 一次函数的应用(费用最低)】
【例4】(2021春 广安期末)为积极响应垃圾分类的号召,某街道决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱.已知购买3个垃圾箱和2个温馨提示牌需要280元,购买2个垃圾箱和3个温馨提示牌需要270元.
(1)每个垃圾箱和每个温馨提示牌各多少元?
(2)若购买垃圾箱和温馨提示牌共100个(两种都买),且垃圾箱的个数不少于温馨提示牌个数的3倍,请写出总费用w(元)与垃圾箱个数m(个)之间的函数关系式,并说明当购买垃圾箱和温馨提示牌各多少个时,总费用最低,最低费用为多少元?
【变式4-1】(2021春 环江县期末)某县园林局打算购买三角梅、水仙装点城区道路,负责人小李去花卉基地调查发现:购买1盆三角梅和2盆水仙需要14元,购买2盆三角梅和1盆水仙需要13元.
(1)求三角梅、水仙的单价各是多少元?
(2)购买三角梅、水仙共10000盆,且购买的三角梅不少于3000盆,但不多于5000盆.
①设购买的三角梅种花a盆,总费用为W元,求W与a的关系式;
②当总费用最少时,应选择哪一种购买方案?最少费用为多少元?
【变式4-2】(2021 三水区校级二模)截至2021年4月10日,全国累计报告接种新冠疫苗16447.1万剂次,接种总剂次数为全球第二.某社区有80000人每人准备接种两剂次相同厂家生产的新冠疫苗并被分配到A、B两个接种点,A接种点有5个接种窗口,B接种点有4个接种窗口.每个接种窗口每天的接种量相同,并且在独立完成20000人的两剂次新冠疫苗接种时,A接种点比B接种点少用5天.
(1)求A、B两个接种点每天接种量;
(2)设A接种点工作x天,B接种点工作y天,刚好完成该社区80000人的新冠疫苗接种任务,求y关于x的函数关系式;
(3)在(2)的条件下,若A接种点每天耗费6.5万元,B接种点每天耗费为4万元,且A、B两个接种点的工作总天数不超过85天,则如何安排A、B两个接种点工作的天数,使总耗费最低?并求出最低费用.
【变式4-3】(2021春 大同期末)在新冠疫情防控期间,某校新购进A、B两种型号的电子体温测量仪共20台,其中A型仪器的数量不少于B型仪器的,已知A、B两种测温仪的价格如表所示,请问购买A、B两种测温仪各多少台时,可使所购仪器的总费用最少?最少需多少元?
型号 A B
价格 800元/台 600元/台
【题型5 一次函数的应用(工程问题)】
【例5】(2021 汇川区三模)为了主题为“醉美遵义,酒都仁怀”第十三届遵义文化旅游产业发展大会召开,仁怀某社区计划对面积为2000m2的区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2.5倍,并且在独立完成面积为500m2区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数解析式.
(3)若甲队每天绿化费用是1.5万元,乙队每天绿化费用为0.5万元,且甲乙两队施工的总天数不超过19天,则如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低费用.
【变式5-1】(2021春 青羊区期末)甲、乙两个工程队分别同时铺设两条公路,所铺设公路的长度y(m)与铺设时间x(h)之间的关系如图所示,根据图象所提供的信息分析,解决下列问题:
(1)在2时~6时段时,乙队的工作效率为 5 m/h;
(2)分别求出乙队在0时~2时段和2时~6时段,y与x的关系式,并求出甲乙两队所铺设公路长度相等时x的值;
(3)求出当两队所铺设的公路长度之差为5m时x的值.
【变式5-2】(2021春 沙坪坝区校级期末)甲、乙两人同时开始共同组装一批零件,工作两小时后,乙因事离开,停止工作.一段时间后,乙重新回到岗位并提高了工作效率.最后40分钟,甲休息,由乙独自完成剩余零件的组装.甲在工作过程中工作效率保持不变,乙在每个工作阶段的工作效率保持不变.甲、乙两人组装零件的总数y(个)与工作时间x(小时)之间的图象如图.
(1)这批零件一共有多少个?
(2)在整个组装过程中,当甲、乙各自组装的零件总数相差40个时,求x的值.
【变式5-3】(2020秋 郑州期末)工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间t(时),甲组加工零件的数量为y甲(个),乙组加工零件的数量为y乙(个),其函数图象如图所示.
(1)求y乙与t之间的函数关系式,并写出t的取值范围;
(2)求a的值,并说明a的实际意义;
(3)甲组加工多长时间时,甲、乙两组加工零件的总数为480个.
【题型6 一次函数的应用(其他问题)】
【例6】(2021春 沙河口区期末)为预防疫情传播,学校对教室定期喷药消毒.如图为一次消毒中,某教室每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)的函数图象,它是由关闭门窗集中喷药,通风前和打开门窗后通风三段不同的一次函数组成的.在下面四个选项中,错误的是( )
A.经过5min集中喷药,教室每立方米空气中含药量最高达到10mg/m3
B.持续11min室内空气中的含药量不低于8mg/m3
C.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才有效杀灭病毒.由此判断此次消毒有效
D.当室内空气中的含药量低于4mg/m3时,对人体是安全的.从室内空气中的含药量达到10mg/m3开始,需经过40min后学生才能进入室内
【变式6-1】(2021春 朝阳区校级期末)某地自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.
(1)某月该单位用水3200吨,水费是 元;若用水2800吨,水费是 元;
(2)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式;
(3)若某月该单位缴纳水费1540元,则该单位这个月的用水量为多少吨?
【变式6-2】(2021春 河东区期末)一个水库的水位在某段时间内持续上涨,表格中记录了连续5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
0 1 2 3 4 5
3 3.3 3.6 3.9 4.2 4.5
(1)水位高度y是否为时间x的函数?若是,请求出这个函数解析式;
(2)据估计,这种上涨规律还会持续,并且当水位高度达到8m时,水库报警系统会自动发出警报.请预测再过多久系统会发出警报?
【变式6-3】(2021 涧西区三模)某大型商场为了提高销售人员的积极性,对原有的薪酬计算方式进行了修改,设销售人员一个月的销售量为x(件),销售人员的月收入为y(元),原有的薪酬计算方式y1元采用的是底薪+提成的方式,且y1=k1x+b,已知每销售一件商品另外获得15元的提成修改后的薪酬计算方式为y2(元),且y2=k2x+b,根据图象回答下列问题:
(1)求y1和y2的解析式,并说明b的实际意义;
(2)求两个函数图象的交点F的坐标,并说明交点F的实际意义;
(3)根据函数图象请判断哪种薪酬计算方式更适合销售人员.
一次函数的应用-重难点题型
【知识点1 一次函数与实际问题】
在研究有关一次函数的实际问题时,要遵循一审、二设、三列、四解的方法:
第1步:审题。认真读题,分析题中各个量之间的关系;
第2步:设自变量。根据各个量之间的关系设满足题意的自变量;
第3步:列函数。根据各个量之间的关系列出函数;
第4步:求解。求出满足题意的数值。
【题型1 一次函数的应用(行程问题)】
【例1】(2021春 海门市期中)甲、乙两人分别从笔直道路上的A、B两地同时出发相向匀速而行,已知甲比乙先出发6分钟,两人在C地相遇,相遇后甲立即按原速原路返回A地,乙继续向A地前行,约定先到A地者停止运动就地休息.若甲、乙两人相距的路程y(米)与甲行走的时间x(分钟)之间的关系如图所示,有下列说法:①甲的速度是60米/分钟,乙的速度是80米/分钟;②甲出发30分钟时,两人在C地相遇;③乙到达A地时,甲与A地相距450米,其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
【解题思路】根据图象可知A、B两地相距3720米;利用速度=路程÷时间可求出甲、乙的速度,由二者相遇的时间=6+A、B两地之间的路程÷二者速度和,可求出二者相遇的时间,再由A、C两地之间的距离=甲的速度×二者相遇的时间可求出A、C两地之间的距离,由A、C两地之间的距离结合甲、乙的速度,可求出乙到达A地时甲与A地相距的路程.
【解答过程】解:由图象可知,A、B两地相距3720米,
甲的速度为(3720﹣3360)÷6=60(米/分钟),
乙的速度为(3360﹣1260)÷(21﹣6)﹣60=80(米/分钟),故①说法正确;
甲、乙相遇的时间为6+3360÷(60+80)=30(分钟),故②说法正确;
A、C两地之间的距离为60×30=1800(米),
乙到达A地时,甲与A地相距的路程为1800﹣1800÷80×60=450(米).故③说法正确.
即正确的说法有4个.
故选:D.
【变式1-1】(2021春 巴彦淖尔期末)如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,判断下列结论正确的选项是( )
①汽车在行驶途中停留了0.5h;
②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;
④汽车出发4h离出发地40km.
A.①②④ B.①②③ C.①③④ D.①②③④
【解题思路】根据停留时距离S不发生变化可判断①;根据速度=路程÷时间列式计算即可判断②;求得往返的路程和得出答案即可判断③;先求出3h到4.5h的速度,再求据出发地的距离可判断④.
【解答过程】解:①汽车在行驶途中停留了2﹣1.5=0.5h,
故①正确;
②平均速度:120×2÷4.5千米/小时,
故②错误;
③汽车共行驶了120×2=240km,
故③正确;
④汽车自出发后3h到4.5h速度为:120÷(4.5﹣3)=120÷1.5=80千米/小时,
∴汽车出发4h离出发地距离为120﹣(4﹣3)×80=120﹣80=40千米,
故④正确.
∴正确的是①③④,
故选:C.
【变式1-2】(2021 沙坪坝区校级开学)某天上午,大学生小南从学校出发去重庆市图书馆查阅资料,同时他的同学小开从该图书馆看完书回学校.两人在途中相遇,于是马上就各自最近的研究课题交流了6分钟,又各自按原速前往自己的目的地.直到小开回到学校并电话告知小南后,小南决定提速25%到达图书馆(接打电话的时间忽略不计).在整个运动过程中,小南和小开之间的距离y(m)与小南所用的时间x(min)之间的函数关系如图所示,则下列说法中正确的是( )
A.学校和图书馆的之间的距离为1200m
B.小南提速前,小开的速度是小南的1.8倍
C.m=1500
D.n=62
【解题思路】从图象上直接可以得出图书馆到学校的距离,从而可以判断A;先求出小南和小开的和速度,再求出小开的速度,从而可以判断B;通过图象和题意可以求出m,从而可以判断C;先求出小南提速后的速度,再根据路程÷速度=时间,即可判断D.
【解答过程】解:由图象可知:图书馆到学校的距离为2400米,
故A错误;
小南和小开的和速度为:2400÷24=100(米/分),
小开走完2400米所用时间为:46﹣6=40(分),
∴小开的速度为:2400÷40=60(米/分),
∴小南的速度为:100﹣60=40(米/分),
∴小南提速前,小开的速度是小南的60÷40=1.5,
故B错误;
相遇后到小开到达学校所用时间为46﹣(24+6)=16(分),
∴m=100×16=1600(米),
故C错误;
小南提速后的速度为40(1+25%)=50(米/分),
∴n=(2400﹣1600)÷50+46=16+46=62(分),
故D正确.
故选:D.
【变式1-3】(2021 蒙阴县二模)甲、乙两车从M地到480千米的N地,甲车比乙车晚出发2小时,乙车途中因故停车检修,图中线段DE、折线OABC分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数图象,请根据图象所提供的信息,解决如下问题:
(1)求两车在途中第二次相遇时,它们距目的地的路程;
(2)甲车出发多长时间,两车在途中第一次相遇?
【解题思路】(1)设甲车所行使路程y与时间x的函数关系式为y=k1x+b1,利用待定系数法求出其函数关系式,再结合交点F的横坐标解答即可;
(2)求出线段BC对应的函数关系式,求出点P的坐标,计算两车在途中第一次相遇的时间.
【解答过程】解:(1)设甲车所行使路程y与时间x的函数关系式为y=k1x+b1,
把(2,0)和(10,480)代入,得,
解得:,
∴y与x的函数关系式为y=60x﹣120;
由图可得,交点F表示第二次相遇,F点的横坐标为6,此时y=60×6﹣120=240,
∴F(6,240),
故两车在途中第二次相遇时它们距目的地的路程为480﹣240=240(千米);
(2)设线段BC对应的函数关系式为y=k2x+b2,
把(6,240)、(8,480)代入,得,
解得,
故y与x的函数关系式为y=120x﹣480,
则当x=4.5时,y=120×4.5﹣480=60.
可得:点B的纵坐标为60,
∵线段AB表示因故停车检修,
∴交点P的纵坐标为60,
把y=60代入y=60x﹣120中,
有60=60x﹣120,
解得x=3,
则交点P的坐标为(3,60),
∵交点P表示第一次相遇,
∴甲车出发的时间为:3﹣2=1(小时).
【题型2 一次函数的应用(调运问题)】
【例2】(2021春 大安市期末)A城有肥料400吨,B城有肥料300吨,现要把这些肥料全部运往C、D两乡镇,从A城运往C、D两乡镇肥料费为20元/吨和25元/吨;从B城往C、D两乡镇运肥料的费用分别为15元/吨和24元/吨,C乡镇需要肥料340吨,D乡镇需要肥料360吨.设A城运往C乡镇x吨肥料,请解答下列问题:
(1)根据题意,填写下列表格:
城、乡/吨数 C D
A x 400﹣x
B 340﹣x x﹣40
(2)设总运费为W(元),求出W(元)与x(吨)的函数关系式,并写出自变量的取值范围;
(3)求怎样调运可使总运费最少?最少为多少元?
【解题思路】(1)根据题意,可以将表格补充完整;
(2)根据题意和(1)中表格的数据,可以写出W(元)与x(吨)的函数关系式,并写出自变量的取值范围;
(3)根据(2)中函数关系式和一次函数的性质,可以得到怎样调运可使总运费最少,最少为多少元.
【解答过程】解:(1)根据题意,表格填写如下:
城、乡/吨数 C D
A x 400﹣x
B 340﹣x x﹣40
故答案为:400﹣x;340﹣x;x﹣40;
(2)由题意可得,
W=20x+25(400﹣x)+15(340﹣x)+24(x﹣40)=4x+14140,
∵340﹣x≥0且x﹣40≥0,
∴40≤x≤340,
即W(元)与x(吨)的函数关系式是W=4x+14140(40≤x≤340);
(3)∵y=4x+14140,k=4>0,
∴y随x的增大而增大,
∵40≤x≤340,
∴当x=40时,y取得最小值,此时y=14300,400﹣x=360,340﹣x=300,x﹣40=0,
答:从A城运往C乡40吨,运往D乡360吨;从B城运往C乡300吨,运往D乡0吨,此时总运费最少,总运费最小值是14300元.
【变式2-1】(2021 寻乌县模拟)疫情期间,甲、乙两个仓库要向M,N两地运送防疫物资,已知甲仓库可调出50吨防疫物资,乙仓库可调出40吨防疫物资,M地需35吨防疫物资,N地需55吨防疫物资,两仓库到M,N两地的路程和运费如下表:
路程/千米 运送1千米所需运费/(元/吨)
甲仓库 乙仓库 甲仓库 乙仓库
M地 20 15 12 12
N地 25 20 10 8
(1)设从甲仓库运往M地防疫物资x吨,两仓库运往M,N两地的总费用为y元,求y关于x的函数关系式.
(2)如何调运才能使总运费最少?总运费最少是多少?
【解题思路】(1)设甲仓库运往M地的防疫物资为x吨,甲仓库运往N地的防疫物资为(50﹣x)吨,乙仓库运往M地的防疫物资为(35﹣x)吨,乙仓库运往N地的防疫物资为(5+x)吨,根据题意列出函数解析式,并求出自变量的取值范围;
(2)根据一次函数的性质以及自变量的取值范围求出函数最小值.
【解答过程】解:设甲仓库运往M地的防疫物资为x吨,甲仓库运往N地的防疫物资为(50﹣x)吨,
乙仓库运往M地的防疫物资为(35﹣x)吨,乙仓库运往N地的防疫物资为(5+x)吨,
根据题意得:y=12×20x+10×25(50﹣x)+12×15×(35﹣x)+8×20(5+x)
=﹣30x+19600,
∵x≥0,50﹣x≥0,35﹣x≥0,
∴0≤x≤35,
∴y关于x的函数关系式为y=﹣30x+19600(0≤x≤35);
(2)∵y=﹣30x+19600,﹣30<0,
∴y随x的增大而减小,
∵0≤x≤35,
∴当x=35时,总运费最少,
即从甲仓库运往M地35吨,
甲仓库运往N地:50﹣35=15(吨),
乙仓库运往M地:55﹣15=40(吨),
乙仓库运往N地:40﹣40=0(吨),
∴总运费最少为:﹣30×35+19600=18550(元).
∴从甲仓库运往M地35吨,运往N地15吨;从乙仓库运往N地40吨时总运费最少,总运费最少是18550元.
【变式2-2】(2021春 满洲里市期末)已知A地有蔬菜200t,B地有蔬菜300t,现决定将这些蔬菜全部调运给C,D两地,C,D两地分别需要调运蔬菜240t和260t.其中从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C地的蔬菜为x吨.设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案.
【解题思路】根据从B地运往C地的蔬菜为x吨,可以用含x的式子表示出运往各地的吨数,然后即可写出w与x的函数关系式,再根据一次函数的性质和x的取值范围,即可得到总运费最小的调运方案,
【解答过程】解:设从B地运往C地的蔬菜为x吨,则从B地运往D地的蔬菜为(300﹣x)吨,从A地运往C地的蔬菜为(240﹣x)吨,从A地运往D地的蔬菜为(x﹣40)吨.
w=20(240﹣x)+25(x﹣40)+15x+18(300﹣x)=2x+9200,
由题意得,,
解得40≤x≤240,
∵w=2x+9200,k=2>0,
∴w随x的增大而增大,
∴当x=40时,总运费w有最小值9280元,240﹣x=200,x﹣40=0,300﹣x=260,
答:w与x之间的函数关系式是w=2x+9200,总运费最小的调运方案是从A地运往C地200吨,B地运往C地40吨,B地运往D地260吨.
【变式2-3】(2021春 昆明期末)某市A、B两个仓库分别有救灾物资200吨和300吨,2021年5月18日起云南大理州漾濞县已连续发生多次地震,最高震级为5月21日发生的6.4级地震,为援助灾区,现需将这些物资全部运往甲,乙两个受灾村.已知甲村需救灾物资240吨,乙村需救灾物资260吨,从A仓库运往甲,乙两村的费用分别为每吨20元和每吨25元,从B仓库运往甲,乙两村的费用分别为每吨15元和24元.设A仓库运往甲村救灾物资x吨,请解答下列问题:
(1)根据题意,填写下表格:
仓库 甲村 乙村
A x ①
B ② ③
①= 200﹣x ;②= 240﹣x ;③= x+60 .
(2)设总运费为W(元),求出W(元)与x(吨)的函数关系式.
(3)求怎么调运可使总运费最少?最少运费为多少元?
【解题思路】(1)根据题意用含x的代数式表示即可;
(2)根据题意直接列式:y=20x+25(200﹣x)+15(240﹣x)+24(x+60)化简即可;
(3)由(2)中的一次函数可知,y随x的减小而减小,要使总运费最低,x必须取最小值,计算各个运货数量设计方案即可.
【解答过程】解:(1)∵A、B两个仓库分别有救灾物资200吨和300吨,甲村需救灾物资240吨,乙村需救灾物资260吨,
∴设A仓库运往甲村救灾物资x吨,则运往乙村(200﹣x)吨,B仓库运往甲村(240﹣x)吨,运往乙村[300﹣(240﹣x)]=(x+60)吨,
∴①=200﹣x,②=240﹣x,③=x+60.
故答案为:200﹣x,240﹣x,x+60.
(2)W=20x+25(200﹣x)+15(240﹣x)+24(x+60)=4x+10040(0≤x≤200).
(3)∵一次函数W=4x+10040,k=4>0,
∴y随x的减小而减小,
∴要使总运费最低,x必须取最小值.
∴当x=6时,总运费最少是10040元.
调运方案为:从A村运往乙库200吨,从B村运往甲库240吨,运往乙库60吨.
【题型3 一次函数的应用(利润最大化)】
【例3】(2021 镇雄县二模)2020年6月1日上午,国务院总理在山东烟台考察时表示,地摊经济是就业岗位的重要来源,是人间的烟火,和“高大上”一样,是中国的生机.“地摊经济”成为了社会关注的热门话题.小明从市场得知如表信息:
甲商品 乙商品
进价(元/件) 35 5
售价(元/件) 45 8
小明计划购进甲、乙商品共100件进行销售,设小明购进甲商品x件,甲、乙商品全部销售完后获得利润为y元.
(1)求出y与x之间的函数关系式;
(2)小明用不超过2000元资金一次性购进甲,乙两种商品,求x的取值范围;
(3)在(2)的条件下,若要求甲,乙商品全部销售完后获得的利润不少于632.5元,请说明小明有哪些可行的进货方案,并计算哪种进货方案的利润最大.
【解题思路】(1)由y=甲商品利润+乙商品利润,可得解析式;
(2)由用不超过2000元资金一次性购进甲,乙两种商品,列出不等式组,即可求解;
(3)由获得的利润不少于632.5元,列出不等式可求x的范围,由一次函数的性质可求解.
【解答过程】解:(1)由题意可得:y=(45﹣35)x+(8﹣5)(100﹣x)=7x+300;
(2)由题意可得:35x+5(100﹣x)≤2000,
∴x≤50,
又∵x≥0,
∴0≤x≤50,且x为整数;
(3)由题意可得:(45﹣35)x+(8﹣5)(100﹣x)≥632.5,
∴x≥47.5,
∴47.5≤x≤50,
又∵x为整数,
∴x=48,49,50,
∴进货方案有:甲商品进48件,乙商品进52件;甲商品进49件,乙商品进51件;甲商品进50件,乙商品进50件;
∵y=7x+300,
∴y随x的增大而增大,
∴当x=50时,有最大利润.
∴当甲商品进50件,乙商品进50件,利润有最大值.
【变式3-1】(2021 青白江区模拟)在近期“抗疫”期间,某药店销售A,B两种型号的口罩,已知销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍,则该药店购进A型、B型口罩各多少只,才能使销售总利润y最大?
【解题思路】(1)设每只A型口罩销售利润为a元,每只B型口罩销售利润为b元,根据“销售80只A型和45只B型的利润为21元,销售40只A型和60只B型的利润为180元”列方程组解答即可;
(2)根据题意即可得出y关于x的函数关系式;根据题意列不等式得出x的取值范围,再结合y关于x的函数关系式解答即可.
【解答过程】解:(1)设每只A型口罩销售利润为a元,每只B型口罩销售利润为b元,根据题意得:
,
解得,
答:每只A型口罩销售利润为0.15元,每只B型口罩销售利润为0.2元;
(2)根据题意得,y=0.15x+0.2(2000﹣x),即y=﹣0.05x+400;
根据题意得,,
解得500≤x≤1000,
∴y=﹣0.05x+400(500≤x≤1000),
∵﹣0.05<0,
∴y随x的增大而减小,
∵x为正整数,
∴当x=500时,y取最大值,则2000﹣x=1500,
即药店购进A型口罩500只、B型口罩1500只,才能使销售总利润最大.
【变式3-2】(2021春 连山区期末)由于新能源汽车越来越受到消费者的青睐,某经销商决定分两次购进甲、乙两种型号的新能源汽车(两次购进同一种型号汽车的每辆的进价相同).第一次用270万元购进甲型号汽车30辆和乙型号汽车20辆;第二次用128万元购进甲型号汽车14辆和乙型号汽车10辆.
(1)求甲、乙两种型号汽车每辆的进价;
(2)经销商分别以每辆甲型号汽车8.8万元,每辆乙型号汽车4.2万元的价格销售后,根据销售情况,决定再次购进甲、乙两种型号的汽车共100辆,且乙型号汽车的数量不少于甲型号汽车数量的3倍,设再次购进甲型汽车a辆,这100辆汽车的总销售利润为W万元.
①求W关于a的函数关系式;并写出自变量的取值范围;
②若每辆汽车的售价和进价均不变,该如何购进这两种汽车,才能使销售利润最大?最大利润是多少?
【解题思路】(1)设甲种型号汽车的进价为a万元、乙种型号汽车的进价为b万元,根据“第一次用270万元购进甲型号汽车30辆和乙型号汽车20辆;第二次用128万元购进甲型号汽车14辆和乙型号汽车10辆”得到相应的二元一次方程组,解方程组即可得到甲、乙两种型号汽车每辆的进价;
(2)①根据题意可以得到利润与购买甲种型号汽车数量的函数关系;
②根据乙型号汽车的数量不少于甲型号汽车数量的3倍,可以得到购买甲种型号汽车数量的取值范围,然后根据一次函数的性质,即可得到最大利润和此时的购买方案.
【解答过程】解:(1)设甲种型号汽车的进价为a万元、乙种型号汽车的进价为b万元,,
解得:,
答:甲、乙两种型号汽车每辆的进价分别为7万元、3万元;
(2)①由题意得:购进乙型号的汽车(100﹣a)辆,
则W=(8.8﹣7)a+(4.2﹣3)×(100﹣a)=0.6a+120,
乙型号汽车的数量不少于甲型号汽车数量的3倍,
∴100﹣a≥3a,且a≥0,
解得,0≤a≤25,
∴W关于a的函数关系式为W=0.6a+120(0≤a≤25);
②W=0.6a+120,
∵0.6>0,
∴W随着a的增大而增大,
∵0≤a≤25,
∴当a=25时,W取得最大值,此时W=0.6×25+120=135(万元),
100﹣25=75(辆),
答:获利最大的购买方案是购进甲型汽车25辆,乙型汽车75辆,最大利润是135万元.
【变式3-3】(2021 鹿邑县一模)草莓是一种极具营养价值的水果,当下正是草莓的销售旺季.某水果店以2850元购进两种不同品种的盒装草莓.若按标价出售可获毛利润1500元(毛利润=售价﹣进价),这两种盒装草莓的进价、标价如表所示:
价格/品种 A品种 B品种
进价(元/盒) 45 60
标价(元/盒) 70 90
(1)求这两个品种的草莓各购进多少盒;
(2)该店计划下周购进这两种品种的草莓共100盒(每种品种至少进1盒),并在两天内将所进草莓全部销售完毕(损耗忽略不计).因B品种草莓的销售情况较好,水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒.如何安排进货,才能使毛利润最大,最大毛利润是多少?
【解题思路】(1)根据某水果店以2850元购进两种不同品种的盒装草莓,按标价出售可获毛利润1500元和表格中的数据,可以列出相应的二元一次方程组,然后求解即可;
(2)根据题意,可以写出毛利润和购买A种草莓数量的函数关系式,然后根据水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒,可以得到相应的不等式,求出A种草莓数量的取值范围,再根据一次函数的性质,即可得到如何安排进货,才能使毛利润最大,最大毛利润是多少.
【解答过程】解:(1)设A品种的草莓购进x盒,B品种的草莓购进y盒,
由题意可得,,
解得,
答:A品种的草莓购进30盒,B品种的草莓购进25盒;
(2)设A品种的草莓购进a盒,则B品种的草莓购进(100﹣a)盒,毛利润为w元,
由题意可得,w=(70﹣45)a+(90﹣60)×(100﹣a)=﹣5a+3000,
∵k=﹣5<0,
∴w随a的增大而减小,
∵水果店计划购进B品种的盒数不低于A品种盒数的2倍,且A品种不少于20盒,
∴,
解得20≤a≤33,
∴当a=20时,w取得最大值,此时w=﹣5×20+3000=2900,100﹣a=80,
答:当A品种的草莓购进20盒,B品种的草莓购进80盒时,才能使毛利润最大,最大毛利润是2900元.
【题型4 一次函数的应用(费用最低)】
【例4】(2021春 广安期末)为积极响应垃圾分类的号召,某街道决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱.已知购买3个垃圾箱和2个温馨提示牌需要280元,购买2个垃圾箱和3个温馨提示牌需要270元.
(1)每个垃圾箱和每个温馨提示牌各多少元?
(2)若购买垃圾箱和温馨提示牌共100个(两种都买),且垃圾箱的个数不少于温馨提示牌个数的3倍,请写出总费用w(元)与垃圾箱个数m(个)之间的函数关系式,并说明当购买垃圾箱和温馨提示牌各多少个时,总费用最低,最低费用为多少元?
【解题思路】(1)根据购买3个垃圾箱和2个温馨提示牌需要280元,购买2个垃圾箱和3个温馨提示牌需要270元,可以列出相应的二元一次方程组,然后求解即可;
(2)根据题意,可以写出w与m的函数关系式,然后根据垃圾箱的个数不少于温馨提示牌个数的3倍,即可得到m的取值范围,然后根据一次函数的性质,即可得到当购买垃圾箱和温馨提示牌各多少个时,总费用最低,最低费用为多少元.
【解答过程】解:(1)设每个垃圾箱和每个温馨提示牌分别为x元、y元,
由题意可得,,
解得,
答:每个垃圾箱和每个温馨提示牌分别为60元、50元;
(2)设购买垃圾箱m个,则购买温馨提示牌(100﹣m)个,
w=60m+50(100﹣m)=10m+5000,
∵垃圾箱的个数不少于温馨提示牌个数的3倍,
∴m≥3(100﹣m),
解得m≥75,
∴当m=75时,w取得最小值,此时w=5750,100﹣m=25,
答:总费用w(元)与垃圾箱个数m(个)之间的函数关系式是w=10m+5000,当购买垃圾箱和温馨提示牌分别为75个、25个时,总费用最低,最低费用为5750元.
【变式4-1】(2021春 环江县期末)某县园林局打算购买三角梅、水仙装点城区道路,负责人小李去花卉基地调查发现:购买1盆三角梅和2盆水仙需要14元,购买2盆三角梅和1盆水仙需要13元.
(1)求三角梅、水仙的单价各是多少元?
(2)购买三角梅、水仙共10000盆,且购买的三角梅不少于3000盆,但不多于5000盆.
①设购买的三角梅种花a盆,总费用为W元,求W与a的关系式;
②当总费用最少时,应选择哪一种购买方案?最少费用为多少元?
【解题思路】(1)根据购买1盆三角梅和2盆水仙需要14元,购买2盆三角梅和1盆水仙需要13元,可以列出相应的二元一次方程组,解方程组即可得到三角梅、水仙的单价各为多少元;
(2)①根据题意,可以写出W与m的关系式;
②根据①中的函数关系式和一次函数的性质,即可得到使总花费最少的够花方案,并求出最少费用.
【解答过程】解:(1)设三角梅、水仙的单价分别为x元、y元,
根据题意得,
解得,
答:三角梅、水仙的的单价分别为4元、5元;
(2)①由题意可得,W=4a+5(10000﹣a),
即W与a的关系式是W=﹣a+50000(3000≤a≤5000);
②∵W=﹣a+50000,
∴W随a的增大而减小,
∵3000≤a≤5000,
∴当a=5000时,W取得最小值,
此时W=45000,10000﹣a=1000﹣5000=5000,
答:当购买三角梅、水仙各5000盆时,总花费最少,最少费用为45000元.
【变式4-2】(2021 三水区校级二模)截至2021年4月10日,全国累计报告接种新冠疫苗16447.1万剂次,接种总剂次数为全球第二.某社区有80000人每人准备接种两剂次相同厂家生产的新冠疫苗并被分配到A、B两个接种点,A接种点有5个接种窗口,B接种点有4个接种窗口.每个接种窗口每天的接种量相同,并且在独立完成20000人的两剂次新冠疫苗接种时,A接种点比B接种点少用5天.
(1)求A、B两个接种点每天接种量;
(2)设A接种点工作x天,B接种点工作y天,刚好完成该社区80000人的新冠疫苗接种任务,求y关于x的函数关系式;
(3)在(2)的条件下,若A接种点每天耗费6.5万元,B接种点每天耗费为4万元,且A、B两个接种点的工作总天数不超过85天,则如何安排A、B两个接种点工作的天数,使总耗费最低?并求出最低费用.
【解题思路】(1)设A接种点每天接种量为5x剂次,B接种点每天接种量为4x剂次,由题意:在独立完成20000人的两剂次新冠疫苗接种时,A接种点比B接种点少用5天.列出分式方程,解方程即可;
(2)结合(1)的结论即可得出y关于x的函数关系式;
(3)根据“A、B两个接种点的工作总天数不超过85天”可得x+y≤85,再把(2)的结论代入可得关于x的不等式,解不等式求出x的取值范围;设总耗费为w万元,由题意求出w与x的函数关系式,再根据一次函数的性质解答即可.
【解答过程】解:(1)设A接种点每天接种量为5x剂次,B接种点每天接种量为4x剂次,
由题意得:,
解得:x=400,
经检验,x=400是原方程的解,且符合题意,
则4x=1600,5x=2000,
答:设A接种点每天接种量为2000剂次,B接种点每天接种量为1600剂次;
(2)由(1)得2000x+1600y=80000×2,
∴y100;
(3)由题意,得x+y≤85,
即x+(100)≤85,
解得x≥60,
设总耗费为w万元,
则w=6.5x+4(100)=1.5x+400.
∵1.5>0,
∴w随x的增大而增大,
∴当x=60时,w取值最小,最小值为:1.5×60+400=490(万元),
∴y25,
答:安排A接种点工作60天,B种接种点工作25天,使总耗费最低,最低费用为490万元.
【变式4-3】(2021春 大同期末)在新冠疫情防控期间,某校新购进A、B两种型号的电子体温测量仪共20台,其中A型仪器的数量不少于B型仪器的,已知A、B两种测温仪的价格如表所示,请问购买A、B两种测温仪各多少台时,可使所购仪器的总费用最少?最少需多少元?
型号 A B
价格 800元/台 600元/台
【解题思路】根据题意和表格中的数据,可以写出费用与A种型号测温仪台数的函数关系式,然后根据某校新购进A、B两种型号的电子体温测量仪共20台,A型仪器的数量不少于B型仪器的,可以得到A种型号台数的取值范围,再根据一次函数的性质,即可得到购买A、B两种测温仪各多少台时,可使所购仪器的总费用最少,最少需多少元.
【解答过程】解:设购买A种型号的测温仪x台,则购买B种型号的测温仪(20﹣x)台,所需费用为w元,
由题意可得,w=800x+600(20﹣x)=200x+12000,
∴w随x的增大而增大,
∵某校新购进A、B两种型号的电子体温测量仪共20台,A型仪器的数量不少于B型仪器的,
∴(20﹣x)≤x≤20,
解得8≤x≤20,
∴当x=8时,w取得最小值,此时w=200×8+12000=13600,20﹣x=12,
答:购买A、B两种测温仪分别为8台、12台时,可使所购仪器的总费用最少,最少需13600元.
【题型5 一次函数的应用(工程问题)】
【例5】(2021 汇川区三模)为了主题为“醉美遵义,酒都仁怀”第十三届遵义文化旅游产业发展大会召开,仁怀某社区计划对面积为2000m2的区域进行绿化,经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2.5倍,并且在独立完成面积为500m2区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数解析式.
(3)若甲队每天绿化费用是1.5万元,乙队每天绿化费用为0.5万元,且甲乙两队施工的总天数不超过19天,则如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低费用.
【解题思路】(1)设乙工程队每天能完成绿化的面积是xm2,则乙甲队每天能完成绿化面积2.5xm2,根据在独立完成面积为500m2区域的绿化时,甲队比乙队少用6天,列方程求解;
(2)根据(1)的结论即可求出y与x的函数解析式.
(3)根据甲乙两队施工的总天数不超过19天,得到x的取值范围,设施工总费用为w元,根据题意得出w与x的函数关系式,根据一次函数的性质,即可解答.
【解答过程】解:(1)设乙工程队每天能完成绿化的面积是xm2,则乙甲队每天能完成绿化面积2.5xm2,
根据题意得:,
解得x=50,
经检验,x=50是原方程的解并满足题意,
则甲工程队每天能完成绿化的面积是:50×2.5=125(m2),
答:甲、乙两工程队每天能完成绿化的面积分别是125m2、50m2;
(2)根据题意,得:125x+50y=2000,
整理得:y=40﹣2.5x,
∴y与x的函数解析式为:y=40﹣2.5x;
(3)∵甲乙两队施工的总天数不超过19天,
∴x+y≤19,
∴x+40﹣2.5x≤19,
解得:x≥14,
设施工总费用为w元,根据题意得:
w=1.5x+0.5y=1.5x+0.5×(40﹣2.5x)=0.25x+20,
∵k=0.25>0,
∴w随x减小而减小,
∴当x=14时,w有最小值,最小值为0.25×14+20=23.5(万元),
此时y=19﹣14=5.
答:安排甲队施工14天,乙队施工5天时,施工总费用最低为23.5万元.
【变式5-1】(2021春 青羊区期末)甲、乙两个工程队分别同时铺设两条公路,所铺设公路的长度y(m)与铺设时间x(h)之间的关系如图所示,根据图象所提供的信息分析,解决下列问题:
(1)在2时~6时段时,乙队的工作效率为 5 m/h;
(2)分别求出乙队在0时~2时段和2时~6时段,y与x的关系式,并求出甲乙两队所铺设公路长度相等时x的值;
(3)求出当两队所铺设的公路长度之差为5m时x的值.
【解题思路】(1)根据图象即可求出在2时~6时段时,乙队的工作效率;
(2)根据图中的信息利用待定系数法即可确定函数关系式;再根据函数关系式列方程解答即可;
(3)利用(2)中的函数关系式可以解决问题.
【解答过程】解:(1)在2时~6时段时,乙队的工作效率为:(50﹣30)÷(6﹣2)=5(m/h),
故答案为:5;
(2)当0≤x≤2时,设乙队y与x的函数解析式为y=kx,可得2k=30,解得k=15,即y=15x;
当2≤x≤6时,设y与x的函数解析式为y=nx+m,
可得,
解得,
即y=5x+20,
∴;
10x=5x+20,解得x=4,
即甲乙两队所挖河渠长度相等时x的值为4;
(3)当0≤x≤2时,15x﹣10x=5,解得x=1.
当2<x≤4时,5x+20﹣10x=5,解得x=3,
当4<x≤6时,10x﹣(5x+20)=5,解得x=5.
答:当两队所挖的河渠长度之差为5m时,x的值为1h或3h或5h.
【变式5-2】(2021春 沙坪坝区校级期末)甲、乙两人同时开始共同组装一批零件,工作两小时后,乙因事离开,停止工作.一段时间后,乙重新回到岗位并提高了工作效率.最后40分钟,甲休息,由乙独自完成剩余零件的组装.甲在工作过程中工作效率保持不变,乙在每个工作阶段的工作效率保持不变.甲、乙两人组装零件的总数y(个)与工作时间x(小时)之间的图象如图.
(1)这批零件一共有多少个?
(2)在整个组装过程中,当甲、乙各自组装的零件总数相差40个时,求x的值.
【解题思路】(1)根据题意和函数图象中的数据,可以分别计算出甲的速度、乙开始和后来的速度,然后即可计算出这批零件一共有多少个;
(2)根据(1)中的结果和分类讨论的方法,可以求得x的值.
【解答过程】解:(1)由图象可得,
甲的工作效率是:(690﹣420)÷(5﹣2)=90(个/小时),
乙刚开始的工作效率是:420÷2﹣90=120(个/小时),
乙后来的工作效率是:(1320﹣690)÷(85)﹣90=180(个/小时),
1320+180
=1320+120
=1440(个),
答:这批零件一共有1440个;
(2)当0≤x<2时,
(120﹣90)x=40,
解得x;
当2≤x<5时,
120×2﹣90x=40或90x﹣120×2=40,
解得x=2或x=3;
当5≤x<8时,
90x﹣120×2﹣180(x﹣5)=40或120×2+180(x﹣5)﹣90x=40,
解得x=6或x=7(舍去);
当8x≤8时,
120×2+180(x﹣5)﹣90×(8)=40,
解得x=7;
由上可得,在整个组装过程中,当甲、乙各自组装的零件总数相差40个时,x的值是,2,3,6或7.
【变式5-3】(2020秋 郑州期末)工厂某车间需加工一批零件,甲组工人加工中因故停产检修机器一次,然后以原来的工作效率继续加工,由于时间紧任务重,乙组工人也加入共同加工零件.设甲组加工时间t(时),甲组加工零件的数量为y甲(个),乙组加工零件的数量为y乙(个),其函数图象如图所示.
(1)求y乙与t之间的函数关系式,并写出t的取值范围;
(2)求a的值,并说明a的实际意义;
(3)甲组加工多长时间时,甲、乙两组加工零件的总数为480个.
【解题思路】(1)根据函数图象中的数据,可以得到y乙与t之间的函数关系式,并写出t的取值范围;
(2)根据函数图象中的数据,可以得到甲的速度,然后即可计算出a的值,然后再说明a的实际意义即可;
(3)根据题意,可以列出相应的方程,然后即可得到甲组加工多长时间时,甲、乙两组加工零件的总数为480个.
【解答过程】解:(1)设y乙与t之间的函数关系式是y乙=kt+b,
,
解得,
即y乙与t之间的函数关系式是y乙=120t﹣600(5≤t≤8);
(2)由图象可得,
甲的工作效率为120÷3=40(个/时),
a=120+40×(8﹣4)=280,
即a的值是280,实际意义是当甲加工8小时时,一共加工了280个零件;
(3)设甲组加工c小时时,甲、乙两组加工零件的总数为480个,
120+40(c﹣4)+(120c﹣600)=480,
解得c=7,
即甲组加工7小时时,甲、乙两组加工零件的总数为480个.
【题型6 一次函数的应用(其他问题)】
【例6】(2021春 沙河口区期末)为预防疫情传播,学校对教室定期喷药消毒.如图为一次消毒中,某教室每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)的函数图象,它是由关闭门窗集中喷药,通风前和打开门窗后通风三段不同的一次函数组成的.在下面四个选项中,错误的是( )
A.经过5min集中喷药,教室每立方米空气中含药量最高达到10mg/m3
B.持续11min室内空气中的含药量不低于8mg/m3
C.当室内空气中的含药量不低于5mg/m3且持续时间不低于35分钟,才有效杀灭病毒.由此判断此次消毒有效
D.当室内空气中的含药量低于4mg/m3时,对人体是安全的.从室内空气中的含药量达到10mg/m3开始,需经过40min后学生才能进入室内
【解题思路】根据图象分别求出三段一次函数的解析式即可判断.
【解答过程】解:设三段一次函数的解析式为:y=k1x,y=k2x+b1,y=k3x+b2,
由图象可得,10=5k1,,,
解得k1=2,,,
∴三段函数的解析式为:y=2x,yx+11,yx,
A通过图象可得,经过5min集中喷药,教室每立方米空气中含药量最高达到10mg/m3,故A正确;
B将y=8代入y=2x得x=4,15﹣4=11,因此持续11min室内空气中的含药量不低于8mg/m3,故B正确;
C将y=5代入y=2x得x,将y=5代入yx得x=45,4542.5>35,由此判断此次消毒有效,故C正确;
D将y=4代入yx得x=55,55﹣5=50,由此从室内空气中的含药量达到10mg/m3开始,需经过50min后学生才能进入室内,故D错误;
故选:D.
【变式6-1】(2021春 朝阳区校级期末)某地自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.
(1)某月该单位用水3200吨,水费是 1660 元;若用水2800吨,水费是 1400 元;
(2)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式;
(3)若某月该单位缴纳水费1540元,则该单位这个月的用水量为多少吨?
【解题思路】(1)由2800≤3000,根据“水费=每吨水费×用水量”即可算出此时水费;由3200>3000,根据“水费=3000×0.5+超出部分×0.8”即可算出此时水费;
(2)分0≤x≤3000以及x>3000来考虑,根据“水费=每吨水费×用水量和水费=3000×0.5+超出部分×0.8”即可得出y关于x的函数解析式;
(3)根据用水3000吨的收费可知该单位本月用水量超过3000吨,故把1540代入y=0.8x﹣900求出x即可.
【解答过程】解:(1)某月该单位用水3200吨,水费是:3000×0.5+(3200﹣3000)×0.8=1660(元);
若用水2800吨,水费是:2800×0.5=1400(元).
故答案为:1660,1400;
(2)根据题意,当0≤x≤3000时,y=0.5x;
当x>3000时,y=0.5×3000+0.8×(x﹣3000)=0.8x﹣900,
所以y关于x的函数解析式为:y;
(3)如果该单位一个月用水3000吨,则应交水费:0.5×3000=1500(元),
∵1540>1500,
∴该单位某月用水超过3000吨,
∴把y=1540代入y=0.8x﹣900得:
0.8x﹣900=1540,
解得:x=3050,
∴该单位这个月的用水量为3050吨.
【变式6-2】(2021春 河东区期末)一个水库的水位在某段时间内持续上涨,表格中记录了连续5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
0 1 2 3 4 5
3 3.3 3.6 3.9 4.2 4.5
(1)水位高度y是否为时间x的函数?若是,请求出这个函数解析式;
(2)据估计,这种上涨规律还会持续,并且当水位高度达到8m时,水库报警系统会自动发出警报.请预测再过多久系统会发出警报?
【解题思路】(1)根据题意和表格中的数据可以求得y与x之间的函数解析式;
(2)将y=8代入(1)中的函数解析式,求出x的值,再用x的值减去5即可解答本题.
【解答过程】解:(1)设y与x之间的函数解析式为y=kx+b,
,
解得,
即y与x之间的函数解析式为y=0.3x+3;
(2)把y=8,代入y=0.3x+3,得
8=0.3x+3,
解得,x,
,
答:再过小时后系统会发出警报.
【变式6-3】(2021 涧西区三模)某大型商场为了提高销售人员的积极性,对原有的薪酬计算方式进行了修改,设销售人员一个月的销售量为x(件),销售人员的月收入为y(元),原有的薪酬计算方式y1元采用的是底薪+提成的方式,且y1=k1x+b,已知每销售一件商品另外获得15元的提成修改后的薪酬计算方式为y2(元),且y2=k2x+b,根据图象回答下列问题:
(1)求y1和y2的解析式,并说明b的实际意义;
(2)求两个函数图象的交点F的坐标,并说明交点F的实际意义;
(3)根据函数图象请判断哪种薪酬计算方式更适合销售人员.
【解题思路】(1)根据函数图象中的数据可以求得y1和y2的函数关系式;
(2)联立方程组,解方程组可得点F的坐标,根据题目条件可得F的实际意义;
(3)根据(1)中的函数解析式和(2)中点F的坐标,即可解答本题.
【解答过程】解:(1)∵y1=k1x+b的图象过点(0,3000),
∴b=3000,
又∵每销售一件商品另外获得15元的提成,
∴k1=15,
∴y1=15x+3000,
∵y2=k2x+b的图象过点(100,3000),由图象可得b=0,
∴100k2=3000,
解得k2=30,
∴y2=30x,
∴y1中b的实际意义为底薪为3000元,y2中b的实际意义为底薪为0元;
(2),
解得.
∴F(200,6000),
∴F点的实际意义是当销售200件商品时,两种薪酬计算方式所得薪酬相等为6000元;
(3)结合函数图象可知,当0<x<200时,原有的薪酬计算方式更适合销售人员,
当x=200时,选择两种薪酬计算方式对销售人员一样.
当x>200时,修改后的薪酬计算方式更适合销售人员.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
