3.1投影 浙教版初中数学九年级下册同步练习(含答案)
文档属性
| 名称 | 3.1投影 浙教版初中数学九年级下册同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 523.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-23 17:06:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.1投影浙教版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1.如图,斜坡的顶部有一铁塔,是的中点,是水平的在阳光的照射下,塔影留在坡面上已知铁塔底座宽,塔影长,小明和小华的身高都是同一时刻,小明站在点处,影子在坡面上,小华站在平地上,影子在平地上,两人的影长分别为和,则铁塔高为( )
A. B. C. D.
2.如图,路灯距地面,身高的小明从点处沿所在的直线行走到点时,人影长度( )
A. 变长 B. 变长 C. 变短 D. 变短
3.同一时刻的太阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A. 小明的影子比小强的影子长 B. 小明的影子比小强的影子短
C. 小明的影子和小强的影子一样长 D. 无法判断谁的影子长
4.如图,小红夜晚从路灯下处走到处这一过程中,她在路上的影子( )
A. 逐渐变长 B. 逐渐变短 C. 长度不变 D. 先变短后变长
5.下列结论正确的有
( )
同一时刻,同一公园内的物体在阳光照射下,影子的方向是相同的
物体在任何光线照射下影子的方向都是相同的
物体在路灯照射下,影子的方向与路灯的位置有关
物体在点光源照射下,影子的长短仅与物体的长短有关.
A. 个 B. 个 C. 个 D. 个
6.如图,太阳光线与地面成的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,则皮球的直径是( )
A. B. C. D.
7.小明在太阳光下观察矩形木框的影子,不可能是( )
A. 平行四边形 B. 矩形 C. 线段 D. 梯形
8.某舞台的上方共挂有,,,四个照明灯,当只有一个照明灯亮时,一棵道具树和小玲在照明灯光下的影子如图所示,此时亮的照明灯是( )
A. 灯 B. 灯 C. 灯 D. 灯
9.一张正方形纸片在太阳光下的影子不可能是( )
A. 平行四边形 B. 矩形 C. 梯形 D. 线段
10.同一时刻,同一地点,在阳光下影长为米的小王身高为米,一棵树的影长为米,则这棵树的高度为( )
A. 米 B. 米 C. 米 D. 米
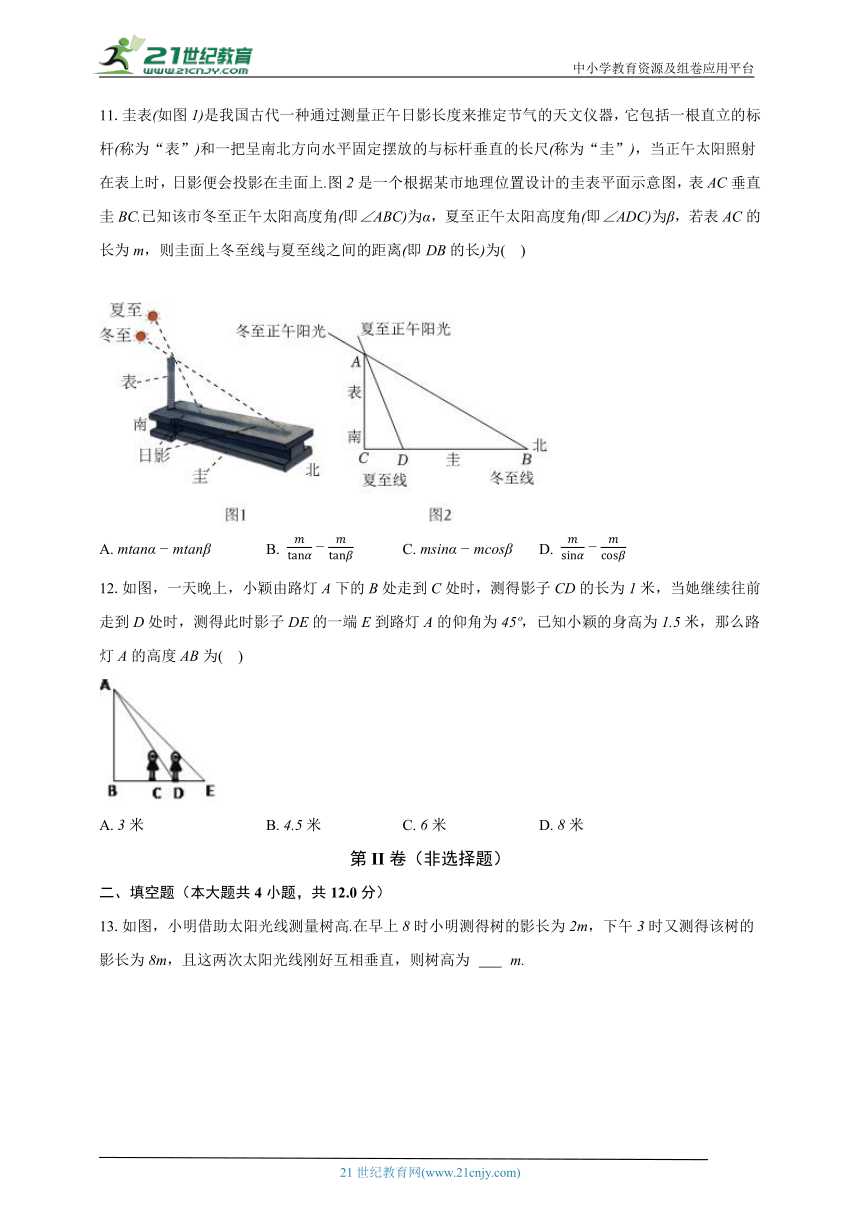
11.圭表如图是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆称为“表”和一把呈南北方向水平固定摆放的与标杆垂直的长尺称为“圭”,当正午太阳照射在表上时,日影便会投影在圭面上图是一个根据某市地理位置设计的圭表平面示意图,表垂直圭已知该市冬至正午太阳高度角即为,夏至正午太阳高度角即为,若表的长为,则圭面上冬至线与夏至线之间的距离即的长为( )
A. B. C. D.
12.如图,一天晚上,小颖由路灯下的处走到处时,测得影子的长为米,当她继续往前走到处时,测得此时影子的一端到路灯的仰角为,已知小颖的身高为米,那么路灯的高度为( )
A. 米 B. 米 C. 米 D. 米
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13.如图,小明借助太阳光线测量树高在早上时小明测得树的影长为,下午时又测得该树的影长为,且这两次太阳光线刚好互相垂直,则树高为
14.如图,小红晚上由路灯下的处走到处时,测得影子的长为米,继续往走米到达处时,测得影子的长为米,已知小明的身高是米,那么路灯离地面的高度的长为______米.
15.如图,甲楼高米,乙楼坐落在甲楼的正北面,已知当地冬至中午时,物高与影长的比是:,已知两楼相距米,那么甲楼的影子落在乙楼上的高____米.结果保留根号
16.小明家的客厅有一张直径为米,高米的圆桌,在距地面米的处有一盏灯,圆桌的影子为,依据题意建立平面直角坐标系如图,其中点的坐标为,则点的坐标是 .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义如图,现将一高度为米的木杆放在灯杆点处为照明灯前米处,沿着方向移动米放置另一个等长木杆.
请分别画出木杆,的影子用线段表示,适当加粗;
若测得木杆影长为米,求木杆的影子长度.
18.本小题分
如图,在直角坐标系中,点是一个光源.木杆两端的坐标分别为,当或时,分别求木杆在轴上的投影的长,从中你有什么发现?
19.本小题分
小明和小亮利用数学知识测量学校操场边升旗台上的旗杆高度.如图,旗杆立在水平的升旗台上,两人测得旗杆底端到升旗台边沿的距离,升旗台的台阶所在的斜坡,坡角为,在太阳光下,小明测得旗杆的影子落在水平地面上的影长长为,同一时刻,小亮测得长的标杆直立于水平地面时的影子长为请你帮小明和小亮求出旗杆的高度.结果保留根号
20.本小题分
如图,一盏路灯点处距离地面米,身高米的小明图中线段与路灯底部处的距离米,
求此时小明在路灯照射下的影长;
若小明想让自己的影长与身高相等,那么他应该向哪个方向走多少米?
21.本小题分
一天某时刻小杰发现学校的旗杆和一篮球架的影子重叠在一起,于是他选择好位置,使得他的影子和它们的影子也重叠在一起即、、在一直线上,如图所示,此时点、、、也在一直线上已知小杰的身高,他的影子长,篮球架的高,且求旗杆的长精确到米.
22.本小题分
如图,小明想利用太阳的影子测量树的高度,他首先在地面上直立一根米的标杆,在测量时,标杆的影子为,此时树的影子一部分落在地面处,另一部分落在墙上处,已知,米,点,,,,,,在同一平面内,求树的高度温馨提示:太阳光与地面以及与地面平行线的夹角相等;为了方便解答,请用图
23.本小题分
如图所示的是一圆柱形笔筒在灯光下的投影,已知该笔筒底面圆的直径,笔筒的高,点在灯光下的投影为点,点在灯光下的投影为点,过点作于点,,点,,,在同一直线上.
求的长;
求点到的距离.
24.本小题分
学习“利用相似三角形测高”的内容后,小涵带着标杆和皮尺来到楼下,发现对面墙上有这栋楼的影子,针对这种情况,她设计了一种测量方案,具体测量情况如下:如示意图,小涵边移动标杆边观察,移动时保持标杆与地面垂直,她发现移动到点处时,可以使标杆落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同此时,测得标杆落在墙上的影子高度,,点,,在同一直线上已知标杆的长度是,请你帮小涵求出楼高.
25.本小题分
先确定图中路灯灯泡的位置,再根据小赵的影子画出表示小赵身高的线段.
答案和解析
1.【答案】
【解析】如解图,过点作,交于点设,,则铁塔高为易知,,,,.
2.【答案】
【解析】【分析】
此题考查相似三角形对应边成比例,应注意题中三角形的变化.小明在不同的位置时,均可构成两个相似三角形,可利用相似比求人影长度的变化.
【解答】
解:设小明在处时影长为,长为,处时影长为.
,,
∽,∽,
,,
则,
;
,
,
,
故变短了米.
故选:.
3.【答案】
【解析】略
4.【答案】
【解析】略
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】解:矩形木框在地面上形成的投影应是平行四边形或一条线段或矩形,
即相对的边平行或重合,
故D不可能,即不会是梯形.
故选:.
在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例,平行物体的影子仍旧平行或重合.
8.【答案】
【解析】略
9.【答案】
【解析】解:一张正方形纸片在太阳光线的照射下,形成影子不可能是梯形,
故选:.
根据平行投影的性质求解可得.
本题主要考查平行投影,解题的关键是掌握平行投影的性质.
10.【答案】
【解析】解:设高度为米,
因为太阳光可以看作是互相平行的,
由相似三角形:,
解得:.
故选:.
在同一时刻物高和影长成正比,即在同一时刻的两个问题物体、影子、经过物体顶部的太阳光线三者构成的两个直角三角形相似.
本题考查相似形的知识,解题的关键在于将题目中的文字转化为数学语言再进行解答.
11.【答案】
【解析】解:在中,,,
,
在中,,
,
,
故选:.
先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义求出的长,从而利用线段的和差关系进行计算,即可解答.
本题考查了解直角三角形的应用,平行投影,熟练掌握锐角三角函数的定义是解题的关键.
12.【答案】
【解析】【分析】
本题考查了中心投影和相似三角形的应用,熟练掌握中心投影的规律是解题的关键.
如图,由已知可得,,设米,米,可得
,则 ,代入各数据可得答案.
【解答】
解:如图所示,
设两个交点分别为、,根据题意得米,
故,
在中, ,
又知,
故,则.
设米,米,
因为,即,,
所以,则 ,
即: ,移项并合并系数化为,解得:,
即米,
故选 B.
13.【答案】
【解析】解:根据题意作图,,,,,
,,
,
,
,
,
,.
故答案为:.
先根据题意作出相应的图,然后可根据条件得到,最后利用相似比即可得解.
本题考查了相似三角形的应用,掌握相似三角形的性质与判定是解题关键.
14.【答案】
【解析】解:,
当小红在处时,∽,即,
当小红在处时,∽,即,
,
米,米,米,米,
设,,
,
解得,
经检验是原方程的根.
,
,
解得.
即路灯的高度米.
故答案为:.
根据在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似解答.
本题综合考查了中心投影的特点和规律以及相似三角形性质的运用.解题的关键是利用中心投影的特点可知在这两组相似三角形中有一组公共边,利用其作为相等关系求出所需要的线段,再求公共边的长度.
15.【答案】
【解析】【分析】
本题考查了平行投影,解直角三角形的应用,根据物高与影长的比是:,得出的值是解题的关键.设于点,那么在中,,解直角三角形可以求得的长,进而求得即可解题.
【解答】
解:设冬天太阳最低时,甲楼最高处点的影子落在乙楼的处,那么图中的长度就是甲楼的影子在乙楼上的高度,
设于点,那么在中,,米.
物高与影长的比是:,
,
则,
故DE.
故答案为
16.【答案】
【解析】过点作轴,垂足为由题意得米,米,米.,∽,,即
,解得米,米,点的坐标为.
17.【答案】解:如图,线段,线段即为所求;
,
∽,
,
,
米,
,
∽,
,
,
米.
木杆的影子长度为米.
【解析】本题考查的是中心投影,相似三角形的应用有关知识
根据中心投影的性质画出图形即可;
利用相似三角形的性质求解即可
18.【答案】当或时,都为,当光源与木杆的高度一定时,木杆影长也是一定值.
【解析】略
19.【答案】解:延长交于,过作于,
则四边形是矩形,
,,,
,,
,,
,
同一时刻,物高和影长成正比,
,
,
,
【解析】本题考查了解直角三角形坡度坡角问题,平行投影,熟练掌握同一时刻,物高和影长成正比是解题的关键延长交于,过作于,根据矩形的性质得到,,,解直角三角形得到,,根据同一时刻,物高和影长成正比,列方程即可得到结论.
20.【答案】解:设,
,
∽.
.
,
解得:.
答:此时小明在路灯照射下的影长为米.
由题,根据题意,此时小明的影长与身高相等,即,
又,
.
.
米.
又题中米,
小明应该向射线方向走米.
【解析】本题主要考查了相似三角形的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解答问题.
由于,故有∽,即可由相似三角形的性质求解;
类似,若此时小明的影长与身高相等,即,求出此时的即可得解.
21.【答案】解:由题意可知,
∽,
,即,
解得:,
,
.
,
∽,
,即,
解得:.
答:旗杆的长为.
【解析】由题意可知,即得出∽,从而得出,代入数据可求出,从而可求出,进而可求出又易证∽,即得出,代入数据,即可求出的长.
本题考查三角形相似的判定和性质的实际应用.熟练掌握三角形相似的判定定理和其性质是解题关键.
22.【答案】解:如图:延长交延长线于,
,,
∽,
,即,则,
又,,
∽,
,
,
,解得:.
【解析】如图:延长交延长线于,再证∽,运用相似三角形的性质可求得,然后再证∽可得,再用线段的和差求得,然后代入计算即可.
本题主要考查了相似三角形的应用,掌握相似三角形的判定与性质成为解答本题的关键.
23.【答案】解:,
∽,
,
,
,
答:的长为;
,
∽,
,
,
,
.
答:点到的距离为.
【解析】根据相似三角形的判定和性质多了即可得到结论;
根据相似三角形的判定和性质多了即可得到结论.
题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
24.【答案】解:如图,过点作,垂足为,交于点,
四边形和四边形都是矩形,
,,,
.
依题意知,,
∽,
,
即,
,
.
答:楼高.
【解析】此题属于实际应用问题,解题的关键是将实际问题转化为数学问题进行解答;解题时要注意构造相似三角形,利用相似三角形的性质解题.
本题考查了相似三角形的应用,把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求解即可,体现了转化的思想.
25.【答案】略
【解析】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.1投影浙教版初中数学九年级下册同步练习
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1.如图,斜坡的顶部有一铁塔,是的中点,是水平的在阳光的照射下,塔影留在坡面上已知铁塔底座宽,塔影长,小明和小华的身高都是同一时刻,小明站在点处,影子在坡面上,小华站在平地上,影子在平地上,两人的影长分别为和,则铁塔高为( )
A. B. C. D.
2.如图,路灯距地面,身高的小明从点处沿所在的直线行走到点时,人影长度( )
A. 变长 B. 变长 C. 变短 D. 变短
3.同一时刻的太阳光下,小明的影子比小强的影子长,那么在同一路灯下( )
A. 小明的影子比小强的影子长 B. 小明的影子比小强的影子短
C. 小明的影子和小强的影子一样长 D. 无法判断谁的影子长
4.如图,小红夜晚从路灯下处走到处这一过程中,她在路上的影子( )
A. 逐渐变长 B. 逐渐变短 C. 长度不变 D. 先变短后变长
5.下列结论正确的有
( )
同一时刻,同一公园内的物体在阳光照射下,影子的方向是相同的
物体在任何光线照射下影子的方向都是相同的
物体在路灯照射下,影子的方向与路灯的位置有关
物体在点光源照射下,影子的长短仅与物体的长短有关.
A. 个 B. 个 C. 个 D. 个
6.如图,太阳光线与地面成的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,则皮球的直径是( )
A. B. C. D.
7.小明在太阳光下观察矩形木框的影子,不可能是( )
A. 平行四边形 B. 矩形 C. 线段 D. 梯形
8.某舞台的上方共挂有,,,四个照明灯,当只有一个照明灯亮时,一棵道具树和小玲在照明灯光下的影子如图所示,此时亮的照明灯是( )
A. 灯 B. 灯 C. 灯 D. 灯
9.一张正方形纸片在太阳光下的影子不可能是( )
A. 平行四边形 B. 矩形 C. 梯形 D. 线段
10.同一时刻,同一地点,在阳光下影长为米的小王身高为米,一棵树的影长为米,则这棵树的高度为( )
A. 米 B. 米 C. 米 D. 米
11.圭表如图是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆称为“表”和一把呈南北方向水平固定摆放的与标杆垂直的长尺称为“圭”,当正午太阳照射在表上时,日影便会投影在圭面上图是一个根据某市地理位置设计的圭表平面示意图,表垂直圭已知该市冬至正午太阳高度角即为,夏至正午太阳高度角即为,若表的长为,则圭面上冬至线与夏至线之间的距离即的长为( )
A. B. C. D.
12.如图,一天晚上,小颖由路灯下的处走到处时,测得影子的长为米,当她继续往前走到处时,测得此时影子的一端到路灯的仰角为,已知小颖的身高为米,那么路灯的高度为( )
A. 米 B. 米 C. 米 D. 米
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13.如图,小明借助太阳光线测量树高在早上时小明测得树的影长为,下午时又测得该树的影长为,且这两次太阳光线刚好互相垂直,则树高为
14.如图,小红晚上由路灯下的处走到处时,测得影子的长为米,继续往走米到达处时,测得影子的长为米,已知小明的身高是米,那么路灯离地面的高度的长为______米.
15.如图,甲楼高米,乙楼坐落在甲楼的正北面,已知当地冬至中午时,物高与影长的比是:,已知两楼相距米,那么甲楼的影子落在乙楼上的高____米.结果保留根号
16.小明家的客厅有一张直径为米,高米的圆桌,在距地面米的处有一盏灯,圆桌的影子为,依据题意建立平面直角坐标系如图,其中点的坐标为,则点的坐标是 .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义如图,现将一高度为米的木杆放在灯杆点处为照明灯前米处,沿着方向移动米放置另一个等长木杆.
请分别画出木杆,的影子用线段表示,适当加粗;
若测得木杆影长为米,求木杆的影子长度.
18.本小题分
如图,在直角坐标系中,点是一个光源.木杆两端的坐标分别为,当或时,分别求木杆在轴上的投影的长,从中你有什么发现?
19.本小题分
小明和小亮利用数学知识测量学校操场边升旗台上的旗杆高度.如图,旗杆立在水平的升旗台上,两人测得旗杆底端到升旗台边沿的距离,升旗台的台阶所在的斜坡,坡角为,在太阳光下,小明测得旗杆的影子落在水平地面上的影长长为,同一时刻,小亮测得长的标杆直立于水平地面时的影子长为请你帮小明和小亮求出旗杆的高度.结果保留根号
20.本小题分
如图,一盏路灯点处距离地面米,身高米的小明图中线段与路灯底部处的距离米,
求此时小明在路灯照射下的影长;
若小明想让自己的影长与身高相等,那么他应该向哪个方向走多少米?
21.本小题分
一天某时刻小杰发现学校的旗杆和一篮球架的影子重叠在一起,于是他选择好位置,使得他的影子和它们的影子也重叠在一起即、、在一直线上,如图所示,此时点、、、也在一直线上已知小杰的身高,他的影子长,篮球架的高,且求旗杆的长精确到米.
22.本小题分
如图,小明想利用太阳的影子测量树的高度,他首先在地面上直立一根米的标杆,在测量时,标杆的影子为,此时树的影子一部分落在地面处,另一部分落在墙上处,已知,米,点,,,,,,在同一平面内,求树的高度温馨提示:太阳光与地面以及与地面平行线的夹角相等;为了方便解答,请用图
23.本小题分
如图所示的是一圆柱形笔筒在灯光下的投影,已知该笔筒底面圆的直径,笔筒的高,点在灯光下的投影为点,点在灯光下的投影为点,过点作于点,,点,,,在同一直线上.
求的长;
求点到的距离.
24.本小题分
学习“利用相似三角形测高”的内容后,小涵带着标杆和皮尺来到楼下,发现对面墙上有这栋楼的影子,针对这种情况,她设计了一种测量方案,具体测量情况如下:如示意图,小涵边移动标杆边观察,移动时保持标杆与地面垂直,她发现移动到点处时,可以使标杆落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同此时,测得标杆落在墙上的影子高度,,点,,在同一直线上已知标杆的长度是,请你帮小涵求出楼高.
25.本小题分
先确定图中路灯灯泡的位置,再根据小赵的影子画出表示小赵身高的线段.
答案和解析
1.【答案】
【解析】如解图,过点作,交于点设,,则铁塔高为易知,,,,.
2.【答案】
【解析】【分析】
此题考查相似三角形对应边成比例,应注意题中三角形的变化.小明在不同的位置时,均可构成两个相似三角形,可利用相似比求人影长度的变化.
【解答】
解:设小明在处时影长为,长为,处时影长为.
,,
∽,∽,
,,
则,
;
,
,
,
故变短了米.
故选:.
3.【答案】
【解析】略
4.【答案】
【解析】略
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】解:矩形木框在地面上形成的投影应是平行四边形或一条线段或矩形,
即相对的边平行或重合,
故D不可能,即不会是梯形.
故选:.
在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例,平行物体的影子仍旧平行或重合.
8.【答案】
【解析】略
9.【答案】
【解析】解:一张正方形纸片在太阳光线的照射下,形成影子不可能是梯形,
故选:.
根据平行投影的性质求解可得.
本题主要考查平行投影,解题的关键是掌握平行投影的性质.
10.【答案】
【解析】解:设高度为米,
因为太阳光可以看作是互相平行的,
由相似三角形:,
解得:.
故选:.
在同一时刻物高和影长成正比,即在同一时刻的两个问题物体、影子、经过物体顶部的太阳光线三者构成的两个直角三角形相似.
本题考查相似形的知识,解题的关键在于将题目中的文字转化为数学语言再进行解答.
11.【答案】
【解析】解:在中,,,
,
在中,,
,
,
故选:.
先在中,利用锐角三角函数的定义求出的长,然后在中,利用锐角三角函数的定义求出的长,从而利用线段的和差关系进行计算,即可解答.
本题考查了解直角三角形的应用,平行投影,熟练掌握锐角三角函数的定义是解题的关键.
12.【答案】
【解析】【分析】
本题考查了中心投影和相似三角形的应用,熟练掌握中心投影的规律是解题的关键.
如图,由已知可得,,设米,米,可得
,则 ,代入各数据可得答案.
【解答】
解:如图所示,
设两个交点分别为、,根据题意得米,
故,
在中, ,
又知,
故,则.
设米,米,
因为,即,,
所以,则 ,
即: ,移项并合并系数化为,解得:,
即米,
故选 B.
13.【答案】
【解析】解:根据题意作图,,,,,
,,
,
,
,
,
,.
故答案为:.
先根据题意作出相应的图,然后可根据条件得到,最后利用相似比即可得解.
本题考查了相似三角形的应用,掌握相似三角形的性质与判定是解题关键.
14.【答案】
【解析】解:,
当小红在处时,∽,即,
当小红在处时,∽,即,
,
米,米,米,米,
设,,
,
解得,
经检验是原方程的根.
,
,
解得.
即路灯的高度米.
故答案为:.
根据在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似解答.
本题综合考查了中心投影的特点和规律以及相似三角形性质的运用.解题的关键是利用中心投影的特点可知在这两组相似三角形中有一组公共边,利用其作为相等关系求出所需要的线段,再求公共边的长度.
15.【答案】
【解析】【分析】
本题考查了平行投影,解直角三角形的应用,根据物高与影长的比是:,得出的值是解题的关键.设于点,那么在中,,解直角三角形可以求得的长,进而求得即可解题.
【解答】
解:设冬天太阳最低时,甲楼最高处点的影子落在乙楼的处,那么图中的长度就是甲楼的影子在乙楼上的高度,
设于点,那么在中,,米.
物高与影长的比是:,
,
则,
故DE.
故答案为
16.【答案】
【解析】过点作轴,垂足为由题意得米,米,米.,∽,,即
,解得米,米,点的坐标为.
17.【答案】解:如图,线段,线段即为所求;
,
∽,
,
,
米,
,
∽,
,
,
米.
木杆的影子长度为米.
【解析】本题考查的是中心投影,相似三角形的应用有关知识
根据中心投影的性质画出图形即可;
利用相似三角形的性质求解即可
18.【答案】当或时,都为,当光源与木杆的高度一定时,木杆影长也是一定值.
【解析】略
19.【答案】解:延长交于,过作于,
则四边形是矩形,
,,,
,,
,,
,
同一时刻,物高和影长成正比,
,
,
,
【解析】本题考查了解直角三角形坡度坡角问题,平行投影,熟练掌握同一时刻,物高和影长成正比是解题的关键延长交于,过作于,根据矩形的性质得到,,,解直角三角形得到,,根据同一时刻,物高和影长成正比,列方程即可得到结论.
20.【答案】解:设,
,
∽.
.
,
解得:.
答:此时小明在路灯照射下的影长为米.
由题,根据题意,此时小明的影长与身高相等,即,
又,
.
.
米.
又题中米,
小明应该向射线方向走米.
【解析】本题主要考查了相似三角形的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解答问题.
由于,故有∽,即可由相似三角形的性质求解;
类似,若此时小明的影长与身高相等,即,求出此时的即可得解.
21.【答案】解:由题意可知,
∽,
,即,
解得:,
,
.
,
∽,
,即,
解得:.
答:旗杆的长为.
【解析】由题意可知,即得出∽,从而得出,代入数据可求出,从而可求出,进而可求出又易证∽,即得出,代入数据,即可求出的长.
本题考查三角形相似的判定和性质的实际应用.熟练掌握三角形相似的判定定理和其性质是解题关键.
22.【答案】解:如图:延长交延长线于,
,,
∽,
,即,则,
又,,
∽,
,
,
,解得:.
【解析】如图:延长交延长线于,再证∽,运用相似三角形的性质可求得,然后再证∽可得,再用线段的和差求得,然后代入计算即可.
本题主要考查了相似三角形的应用,掌握相似三角形的判定与性质成为解答本题的关键.
23.【答案】解:,
∽,
,
,
,
答:的长为;
,
∽,
,
,
,
.
答:点到的距离为.
【解析】根据相似三角形的判定和性质多了即可得到结论;
根据相似三角形的判定和性质多了即可得到结论.
题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力.利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
24.【答案】解:如图,过点作,垂足为,交于点,
四边形和四边形都是矩形,
,,,
.
依题意知,,
∽,
,
即,
,
.
答:楼高.
【解析】此题属于实际应用问题,解题的关键是将实际问题转化为数学问题进行解答;解题时要注意构造相似三角形,利用相似三角形的性质解题.
本题考查了相似三角形的应用,把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求解即可,体现了转化的思想.
25.【答案】略
【解析】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
