特殊平行四边形复习课

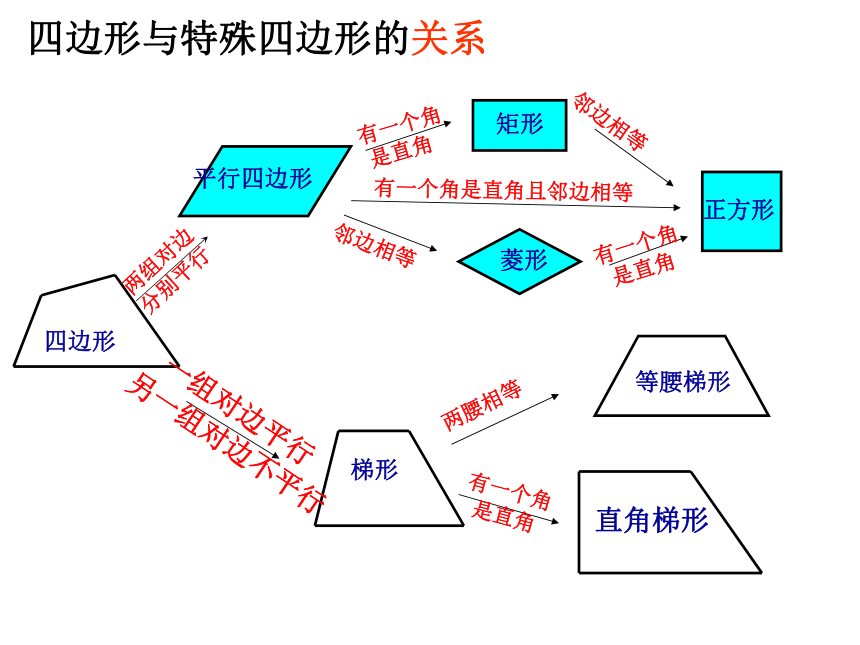
课件27张PPT。《特殊平行四边形》复习四边形与特殊四边形的关系　四边形平行四边形矩形菱形正方形梯形等腰梯形直角梯形两组对边
分别平行有一个角
是直角邻边相等邻边相等有一个角
是直角 一组对边平行
另一组对边不平行两腰相等 有一个角
是直角有一个角是直角且邻边相等平行且相等平行且相等平行
且四边相等平行
且四边相等两底平行
两腰相等对角相等
邻角互补四个角
都是直角同一底上
的角相等对角相等
邻角互补四个角
都是直角互相平分互相平分且相等互相垂直平分，且每一条对角线平分一组对角相等互相垂直平分且相等，每一条对角线平分一组对角中心对称图形中心对称图形
轴对称图形中心对称图形
轴对称图形中心对称图形
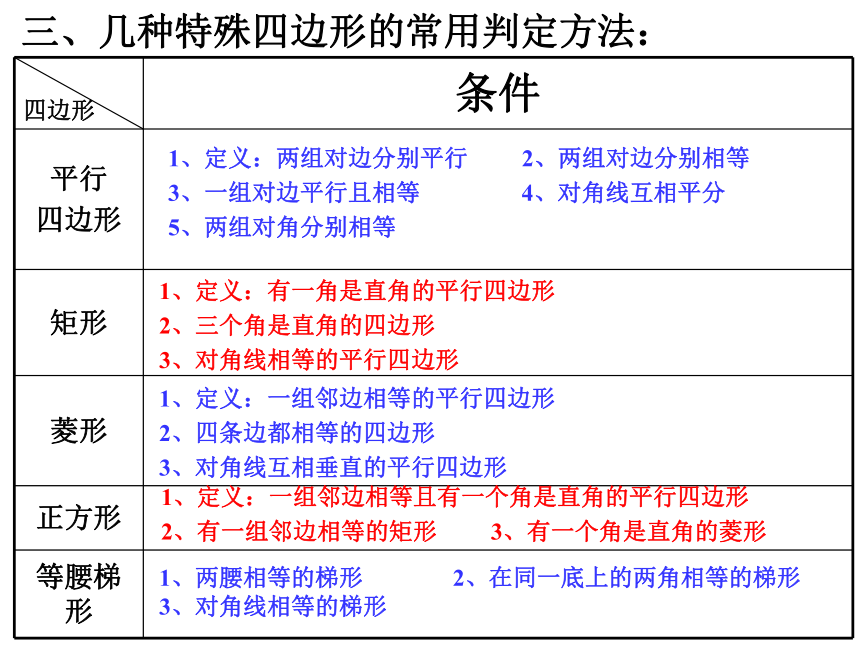
轴对称图形轴对称图形二、几种特殊四边形的性质：三、几种特殊四边形的常用判定方法：1、定义：两组对边分别平行 2、两组对边分别相等
3、一组对边平行且相等 4、对角线互相平分
5、两组对角分别相等1、定义：有一角是直角的平行四边形
2、三个角是直角的四边形
3、对角线相等的平行四边形1、定义：一组邻边相等的平行四边形
2、四条边都相等的四边形
3、对角线互相垂直的平行四边形1、定义：一组邻边相等且有一个角是直角的平行四边形
2、有一组邻边相等的矩形 3、有一个角是直角的菱形1、两腰相等的梯形 2、在同一底上的两角相等的梯形 3、对角线相等的梯形两条对角线__________的四边形是平行四边形
两条对角线__________的平行四边形是矩形
两条对角线________________的四边形是矩形
两条对角线__________的平行四边形是菱形
两条对角线______________的四边形是菱形
两条对角线__________的矩形是正方形
两条对角线__________的菱形是正方形
两条对角线_______________的平行四边形是正方形
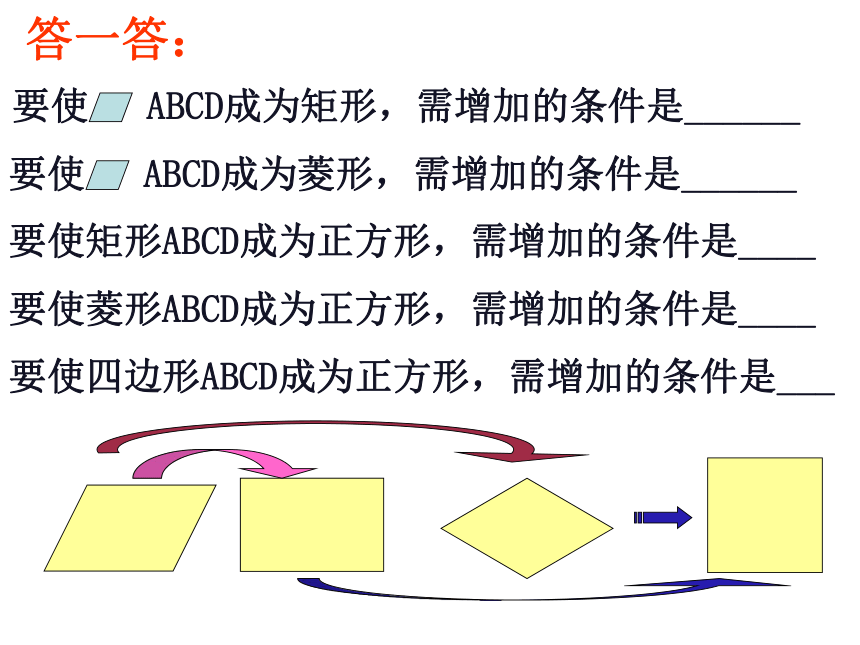
两条对角线___________________的四边形是正方形互相平分互相平分且相等互相垂直平分互相垂直平分且相等相等互相垂直相等互相垂直互相垂直且相等填一填顺次连接平行四边形各边中点所得的四边形是____________顺次连接菱形各边中点所得的四边形是______顺次连接矩形各边中点所得的四边形是______平行四边形矩形菱形请你说说把具有什么特点的四边形的各边中点连接起来能得到正方形呢？想一想：要使矩形ABCD成为正方形，需增加的条件是____ 要使菱形ABCD成为正方形，需增加的条件是____要使四边形ABCD成为正方形，需增加的条件是___答一答：选一选:正方形具有而菱形不具有的性质是( )
A. 对角线互相平分 B. 每条对角线平分一组对角
C. 对角线相等 D.对角线互相垂直
2. 将一个菱形绕两条对角线的交点旋转90。,所得图形与原来的图形重合,此时的菱形是( )
A. 矩形 B.菱形
C. 正方形 D.平行四边形
3.下列图形中不是轴对称图形的是( ),不是中心对称图形的是( )
A. 等腰三角形 B. 平行四边形
C. 菱形 D.正方形CCBADDBC选一选:BCDD辨一辨：1.平行四边形的对角线相等； （ ）2.矩形的四个角都相等； （ ）3.菱形的对角线互相垂直平分； （ ）4.有一个角是直角且邻边相等的平行四边形是正方形； （ ）5.一组对边平行的四边形是梯形； （ ）6.有两个角相等的梯形是等腰梯形； （ ）7.一组对边平行且相等的四边形是平行四边形； （ ）8.对角线相等的四边形是矩形； （ ）9.在梯形中上面的底叫做上底，下面的底叫做下底；（ ）10.正方形既是轴对称图形又是中心对称图形。（ ）例1．如图(3)，正方形ABCD中，AC、BD相交于O， 分析：要证明BM＝CN，大家观察
图形可以考虑证哪两个三角形全等 ?MN∥AB且MN分别交OA、OB于M、N，求证：BM＝CN。　　　　　　　　　 　AB＝BC，∠1＝∠2＝45 °条件够吗？还需要的条件是 AM＝BN△ABM≌△BCN你所要证明的两个三角形已经满足
了哪些条件?由正方形可以得到的条件有：1、已知：正方形ABCD对角线AC、BD相　　　　　　　交于点O，且AB＝acm，如图(2)。
求：AC的长及正方形的面积S。2、已知：在正方形ABCD中，对角线AC、
　BD相交于点O，且AC＝6 cm，如图
求：正方形的面积S。　　　　　　　　　　　 练一练3、已知：如图，ABCD和AKLM都是正方形，求证：MD=KB4、如图，在正方形ABCD中，E在BC的延长线上，且CE=AC，AE交CD于F，则求∠AFC的度数。例2．已知：如图(4)在正方形ABCD中，F为CD延长线
上一点，CE⊥AF于E，交AD于M，
　　 求证：∠MFD＝45°证明：∵CE⊥AF ∴∠ADC＝∠AEM＝90° 又∵∠CMD＝∠AME ∴∠1＝∠2　 又∵CD＝AD，∠ADF＝∠MDC　 ∴Rt△CDM≌Rt△ADF　(AAS) ∴DM=DF ∴∠MFD=450 例3．如图(6)，△ABC的外面作正方形ABDE和ACFG，连结BG、CE，交点为N。求证：∠CEA＝∠ABG　　　　　　　　　　　　　　　 证明：
∵四边形ABDE和四边形ACFG是正方形。 ∴AE＝AB　AG＝AC　∠1＝∠2＝90°又∵∠EAC＝∠1＋∠BAC＝90°＋∠BAC ∠BAG＝∠2＋∠BAC＝90°＋∠BAC　∴∠EAC＝∠BAG　∴△AEC≌△ABG　(SAS)
∴∠CEA＝∠ABG1、如图(5)，在AB上取一点C，以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。求证：(1) △ACF≌△DCB (2) BH⊥AF　　　　　　　　　　　　　　 做一做2、如图，矩形纸片ABCD中，AB=3厘米，BC=4厘米，现将A、C重合，使纸片折叠压平，设折痕为EF。试确定重叠部分△AEF的面积。3、△ABC中，D是AB中点，E是AC上的点，且3AE=2AC，CD、BE交于O点. 求证：OE= BE.80°8㎝ 3、已知：正方形的边长是4㎝，则它的对角线的长是 ，
面积是 。164、已知，正方形的对角线的长是6 ㎝，则它的边长是 ，
面积是 。 填一填几种常见的梯形的辅助线画法：1.构建平行四边形2.平移一条对角线EE3.构建全等三角形F4.构建矩形5.作梯形的中位线6.构建大平行四边形7.构建三角形EO1.已知菱形ABCD中,AE⊥BC于E,AF⊥CD于F,你能判断AE与AF的关系吗？说明理由。2.在矩形ABCD中,两条对角线AC、BD相交于点O, ∠AOB= 60。，AB=3cm。请判定△AOB的形状，并求出对角线的长。做一做拓展练习：1、已知如图，以△ABC的三边为边在BC的同侧分别作三个等边△ABD、△BCE、△ACF，请回答下列问题，并证明。（1）四边形ADEF是什么四边形？（2）探究：当△ABC满足什么条件时，四边形ADEF是矩形；2、有7×6的方格纸型的棋盘，以棋盘上竖线和横线为边，以棋盘中各交叉点为顶点的正方形有 个.你愿意把得到上述结论的探究方法与他人交流吗？在小组中选一个代表简要的讲出你们的探究过程。112再 见