浙江版初二数学期末复习专题-坐标几何与三角形-浙教版(浙江省温州市瑞安市)
文档属性
| 名称 | 浙江版初二数学期末复习专题-坐标几何与三角形-浙教版(浙江省温州市瑞安市) |  | |
| 格式 | rar | ||
| 文件大小 | 55.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-07-03 23:21:00 | ||
图片预览


文档简介
浙江版初二数学期末复习专题——坐标几何与三角形
坐标几何
重点、难点:
1. 在生活和生产实践中,人们常利用一对有序实数来确定物体的位置。
2. 平面直角坐标系是常用的一种坐标系,它由坐标平面、坐标轴以及原点组成。
3. 平面直角坐标系中,图形的变换本质上是点的变换。比如点的对称以及点的平移;今后还会学到由点面组成的平面图形的旋转。
【典型例题】
例1. 到x轴的距离等于2的点能组成一个怎样的图形?
解:由题意,所有到x轴的距离均等于2的点,组成的图形是直线
若设这个距离为d,则|d|=2,∴d=-2或2
∴题设要求的图形是:与x轴平行,且与x轴相距为2的两条直线。
例2. 已知点P到x轴的距离是3,它到原点的距离是5,求点P的坐标。
解:P到原点的距离为5
∴点P在以O为圆心,半径为5的圆上
又点P与x轴相距为3
∴点P在以5为斜边长,一条直角边为3的直角三角形顶点上(如图)
∴容易求得点P共有4个:P1(4,3),P2(4,-3),P3(-4,-3),P4(-4,3)
例3. 已知点M既在过A(3,-2),且与x轴平行的直线上,又在过点B(2,-3),且平行于y轴的直线上,求点M的坐标。
解:过点A(3,-2),且与x轴平行的直线上的所有点,均有纵坐标等于-2的特征……①;同理,过点B(2,-3),且与y轴平行的直线上的所有点,均有横坐标等于2的特征……②;又点M既要满足条件①,又要满足条件②,∴点M一定是M(2,-2)。
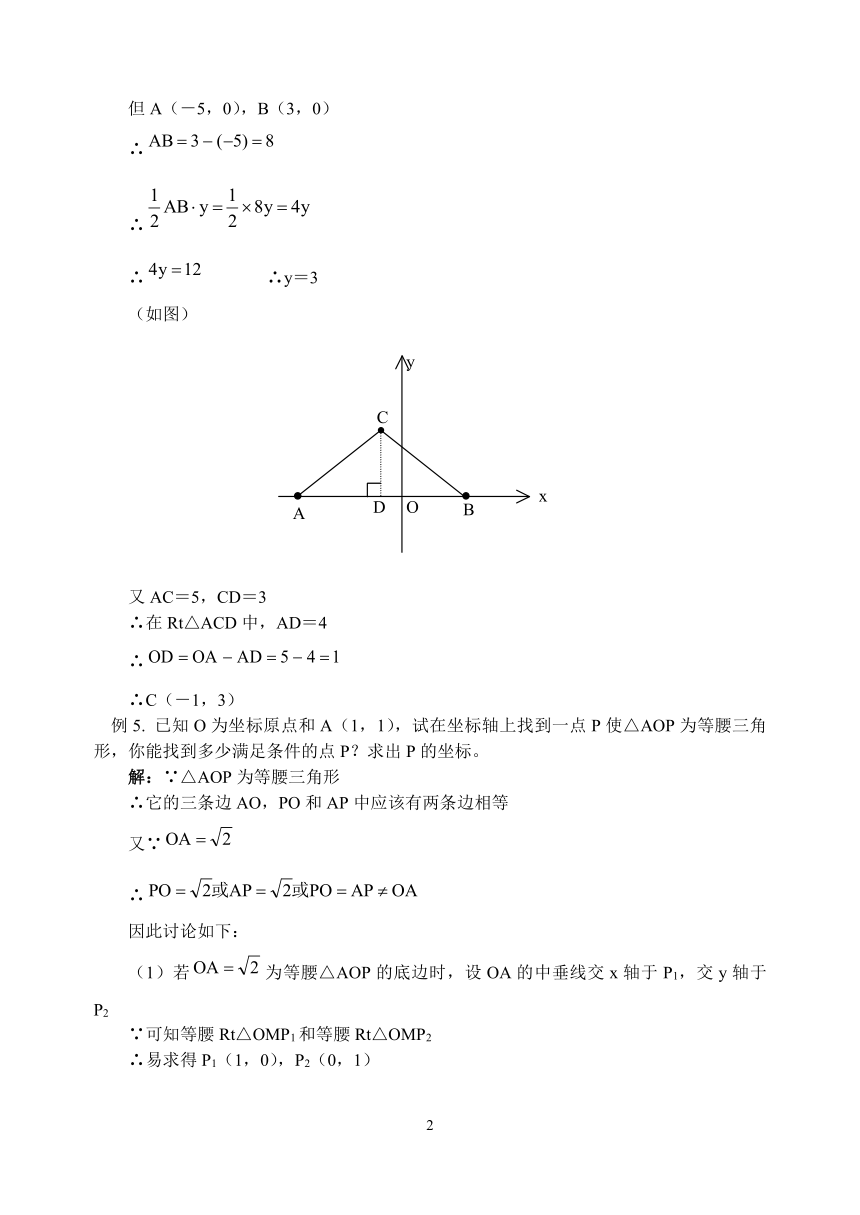
例4. 已知点A(-5,0),B(3,0),且点C在第二象限内。若AC=5,△ABC的面积,求点C的坐标。
解:设点C为(x,y),其中x<0,y>0
则由题意,得
但A(-5,0),B(3,0)
∴
∴
∴ ∴y=3
(如图)
又AC=5,CD=3
∴在Rt△ACD中,AD=4
∴
∴C(-1,3)
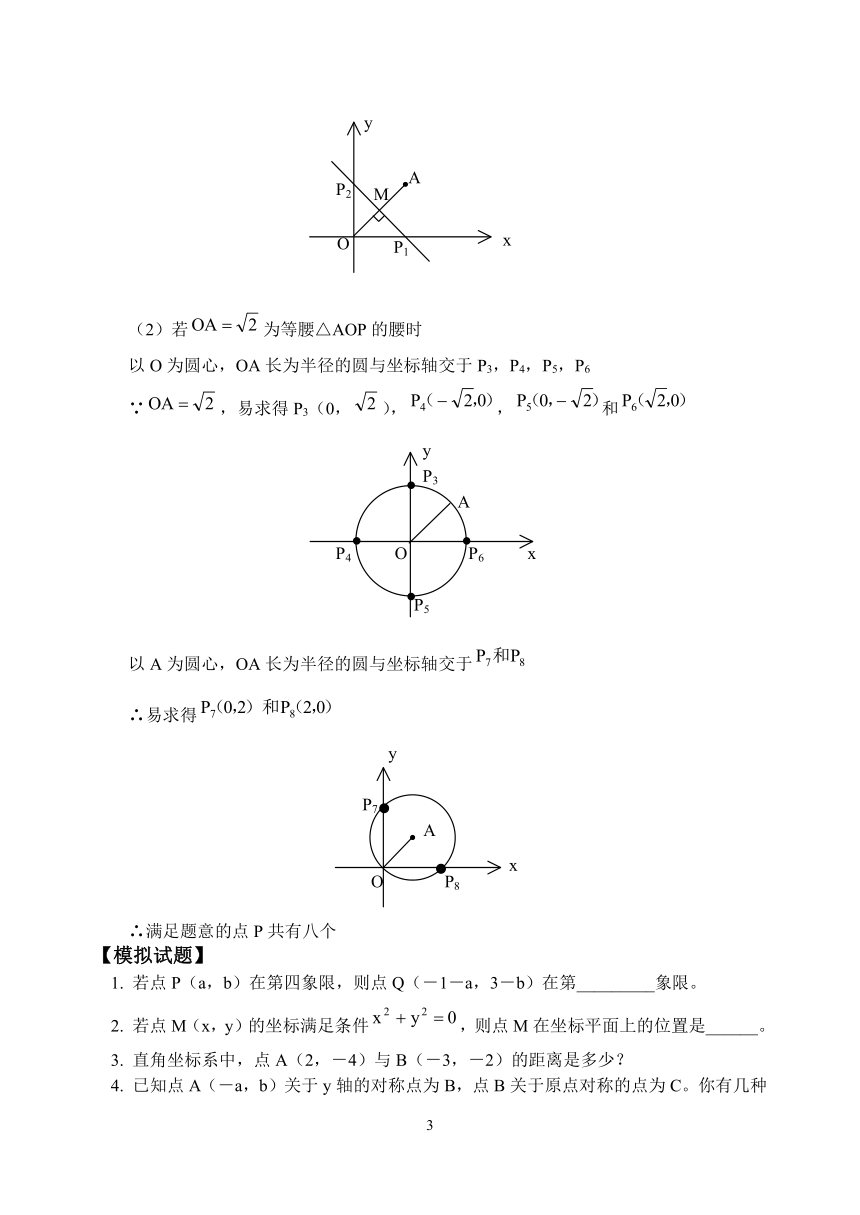
例5. 已知O为坐标原点和A(1,1),试在坐标轴上找到一点P使△AOP为等腰三角形,你能找到多少满足条件的点P?求出P的坐标。
解:∵△AOP为等腰三角形
∴它的三条边AO,PO和AP中应该有两条边相等
又∵
∴
因此讨论如下:
(1)若为等腰△AOP的底边时,设OA的中垂线交x轴于P1,交y轴于P2
∵可知等腰Rt△OMP1和等腰Rt△OMP2
∴易求得P1(1,0),P2(0,1)
(2)若为等腰△AOP的腰时
以O为圆心,OA长为半径的圆与坐标轴交于P3,P4,P5,P6
∵,易求得P3(0,),,和
以A为圆心,OA长为半径的圆与坐标轴交于
∴易求得
∴满足题意的点P共有八个
【模拟试题】
1. 若点P(a,b)在第四象限,则点Q(-1-a,3-b)在第_________象限。
2. 若点M(x,y)的坐标满足条件,则点M在坐标平面上的位置是______。
3. 直角坐标系中,点A(2,-4)与B(-3,-2)的距离是多少?
4. 已知点A(-a,b)关于y轴的对称点为B,点B关于原点对称的点为C。你有几种方法来求出点C的坐标?点C的坐标是多少?
5. 若,则点M(a,b)关于y轴对称的点的坐标是多少?
6. 设以A(-3,7)和B(-3,-2)为端点的线段向左平移了5个长度,请你求出平移后的线段上任意一点的坐标。
7. △ABC中,顶点A、B、C的坐标分别为A(2,-1),B(1,-3)和C(5,-5)。
(1)判断这个三角形的形状。
(2)求△ABC的面积。
8. 已知A(5,-2),B(0,-3),在x,y轴上各找一点P,使得PA=PB。求点P的坐标。
三角形
重点、难点:
1. 等腰三角形的判定与性质
2. 直角三角形的判定与性质
3. 全等三角形的判定与性质
【典型例题】
例1. 如图所示,已知,求A的度数。
解:应当把与所在的三角形一起作联想,然后求A。
∴提示通过三角形的外角定理求解
延长BE交AC于点D
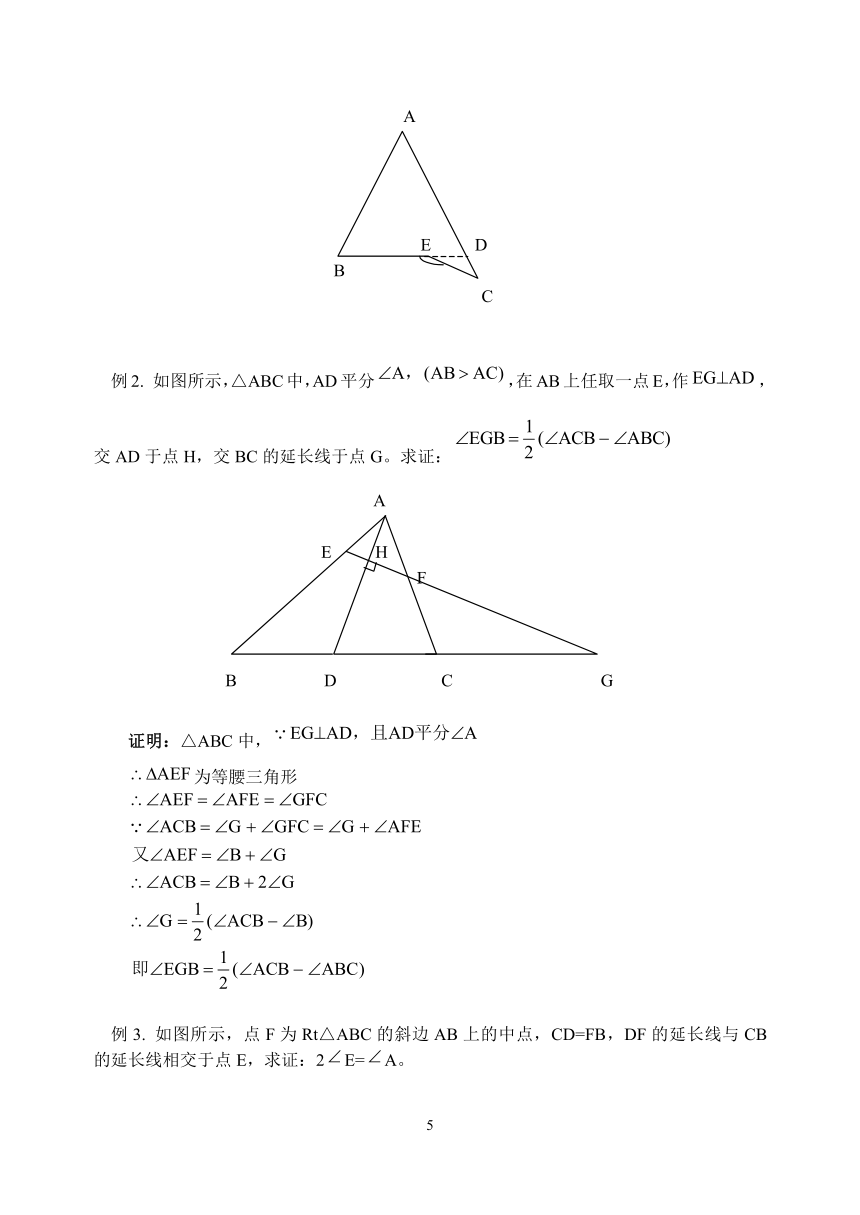
例2. 如图所示,△ABC中,AD平分,在AB上任取一点E,作,交AD于点H,交BC的延长线于点G。求证:
证明:△ABC中,
为等腰三角形
例3. 如图所示,点F为Rt△ABC的斜边AB上的中点,CD=FB,DF的延长线与CB的延长线相交于点E,求证:2E=A。
证明:∵F为Rt△ABC的斜边AB上的中点
∴容易想到“斜中线定理”
∴连CF
∴AF=CF=FB=CD
例4. △ABC中,AD平分,AB+BD=AC,求与C的度数的比值。
解:如图所示,
∴可有两种解法
若
则可在AC上截取AE=AB,连结ED
又AD平分A
但
注:在证明三角形中,已知线段的和,差关系时,常常可运用“截长补短”方法来证明。
例5. Rt△ABC中,AB=AC,A=90°,点D在BC上,;M为BC中点,请判断的形状,并说明你的理由。
解:∵Rt△ABC为等腰直角三角形,且M为BC的中点
∴提示作出底边BC上的高
∴连结AM,则
又AM平分BAC,∴B=EAM
∴FM=EM,∴△MFE为等腰三角形
但注意到FMB=AME
∴可证FME=90°
∴△MEF为等腰直角三角形
例6. 已知一直角三角形两条直角边上的中线长分别为AE=5,,求其斜边AB的长。
解:直角三角形中,求边长或线段长,常常提示运用勾股定理。
如图所示,不妨设Rt△ACB中,C=90°,AC=b,BC=a
则
【模拟试题】
1. 如图所示,已知求A的度数。
2. 如图所示,已知AD是△ABC中BC边上的高,AE是CAF的平分线,AE=2AD,求ACB与B差的度数。
3. Rt△ABC中,C=90°,A=22.5°,D在AC上,DC=BC,于E,求证:AE=BE。
4. △ABC中,AD为BC边上的高,AD=BD,DE=CD,延长BE交AC于F,求证:BF为△ABC中AC边上的高。
5. △ABC中,ACB=90°,D为BC延长线上一点,CD:AB=1:2,若E为AB中点,B的平分线交DE于F,求证:BF=DF。
6. Rt△ABC中,D为AC中点,于E,求证:。
7. 如图所示,已知BD平分ABF,AD=CD,,求证:互补。
8. 如图所示,△ABC中,以AB、AC为边分别向三角形外作正△ABF和正△ACE。BE、CF相交于点O,连结OA,求证:OA平分EOF。
9. 如图所示,△ABC中,AD平分BAC,BE=EC,过点E作,交AC和AD、AB的延长线于H、F、G。求证:。
10. 折叠一张矩形纸片ABCD,先沿对角线BD折叠,再把AD折叠到BD上(如图所示),已知AB=2,BC=1,求第二次折叠的折痕DE的长。
【试题答案】
坐标几何
1. 第二象限
2. 坐标原点
3.
4. C(-a,-b)
5. (-3,-2)
6. 答案不唯一,只要使点符合,,y为任意实数均可以。
7. (1)Rt△ABC,且∠B为直角;(2)
8.
(提示:设,则由PA=PB,得x=2,y=10)
三角形
1.
提示:设A=x,Rt△AFG中,A+G=90°,∴x=15°
2. 60°
3. 略
4. 提示:
5. 提示:连结CE,求证
6. 提示:连结BD,分别对运用勾股定理。
7. 提示:过D作BA的垂线,交BA的延长线于E,证明
8. 提示:过A分别向CF、BE作垂线,垂足分别为M、N
证明全等的一对三角形:△AFC与△ABE对应边上的高相等。
9. 提示:过B作AC的平行线交GH于N
证明,则AC=AH+HC=AB+BG+CH=AB+2BG
10.
提示:设AE=x,则,在Rt△BEF中,运用勾股定理解得,在Rt△ADE中,
PAGE
1
坐标几何
重点、难点:
1. 在生活和生产实践中,人们常利用一对有序实数来确定物体的位置。
2. 平面直角坐标系是常用的一种坐标系,它由坐标平面、坐标轴以及原点组成。
3. 平面直角坐标系中,图形的变换本质上是点的变换。比如点的对称以及点的平移;今后还会学到由点面组成的平面图形的旋转。
【典型例题】
例1. 到x轴的距离等于2的点能组成一个怎样的图形?
解:由题意,所有到x轴的距离均等于2的点,组成的图形是直线
若设这个距离为d,则|d|=2,∴d=-2或2
∴题设要求的图形是:与x轴平行,且与x轴相距为2的两条直线。
例2. 已知点P到x轴的距离是3,它到原点的距离是5,求点P的坐标。
解:P到原点的距离为5
∴点P在以O为圆心,半径为5的圆上
又点P与x轴相距为3
∴点P在以5为斜边长,一条直角边为3的直角三角形顶点上(如图)
∴容易求得点P共有4个:P1(4,3),P2(4,-3),P3(-4,-3),P4(-4,3)
例3. 已知点M既在过A(3,-2),且与x轴平行的直线上,又在过点B(2,-3),且平行于y轴的直线上,求点M的坐标。
解:过点A(3,-2),且与x轴平行的直线上的所有点,均有纵坐标等于-2的特征……①;同理,过点B(2,-3),且与y轴平行的直线上的所有点,均有横坐标等于2的特征……②;又点M既要满足条件①,又要满足条件②,∴点M一定是M(2,-2)。
例4. 已知点A(-5,0),B(3,0),且点C在第二象限内。若AC=5,△ABC的面积,求点C的坐标。
解:设点C为(x,y),其中x<0,y>0
则由题意,得
但A(-5,0),B(3,0)
∴
∴
∴ ∴y=3
(如图)
又AC=5,CD=3
∴在Rt△ACD中,AD=4
∴
∴C(-1,3)
例5. 已知O为坐标原点和A(1,1),试在坐标轴上找到一点P使△AOP为等腰三角形,你能找到多少满足条件的点P?求出P的坐标。
解:∵△AOP为等腰三角形
∴它的三条边AO,PO和AP中应该有两条边相等
又∵
∴
因此讨论如下:
(1)若为等腰△AOP的底边时,设OA的中垂线交x轴于P1,交y轴于P2
∵可知等腰Rt△OMP1和等腰Rt△OMP2
∴易求得P1(1,0),P2(0,1)
(2)若为等腰△AOP的腰时
以O为圆心,OA长为半径的圆与坐标轴交于P3,P4,P5,P6
∵,易求得P3(0,),,和
以A为圆心,OA长为半径的圆与坐标轴交于
∴易求得
∴满足题意的点P共有八个
【模拟试题】
1. 若点P(a,b)在第四象限,则点Q(-1-a,3-b)在第_________象限。
2. 若点M(x,y)的坐标满足条件,则点M在坐标平面上的位置是______。
3. 直角坐标系中,点A(2,-4)与B(-3,-2)的距离是多少?
4. 已知点A(-a,b)关于y轴的对称点为B,点B关于原点对称的点为C。你有几种方法来求出点C的坐标?点C的坐标是多少?
5. 若,则点M(a,b)关于y轴对称的点的坐标是多少?
6. 设以A(-3,7)和B(-3,-2)为端点的线段向左平移了5个长度,请你求出平移后的线段上任意一点的坐标。
7. △ABC中,顶点A、B、C的坐标分别为A(2,-1),B(1,-3)和C(5,-5)。
(1)判断这个三角形的形状。
(2)求△ABC的面积。
8. 已知A(5,-2),B(0,-3),在x,y轴上各找一点P,使得PA=PB。求点P的坐标。
三角形
重点、难点:
1. 等腰三角形的判定与性质
2. 直角三角形的判定与性质
3. 全等三角形的判定与性质
【典型例题】
例1. 如图所示,已知,求A的度数。
解:应当把与所在的三角形一起作联想,然后求A。
∴提示通过三角形的外角定理求解
延长BE交AC于点D
例2. 如图所示,△ABC中,AD平分,在AB上任取一点E,作,交AD于点H,交BC的延长线于点G。求证:
证明:△ABC中,
为等腰三角形
例3. 如图所示,点F为Rt△ABC的斜边AB上的中点,CD=FB,DF的延长线与CB的延长线相交于点E,求证:2E=A。
证明:∵F为Rt△ABC的斜边AB上的中点
∴容易想到“斜中线定理”
∴连CF
∴AF=CF=FB=CD
例4. △ABC中,AD平分,AB+BD=AC,求与C的度数的比值。
解:如图所示,
∴可有两种解法
若
则可在AC上截取AE=AB,连结ED
又AD平分A
但
注:在证明三角形中,已知线段的和,差关系时,常常可运用“截长补短”方法来证明。
例5. Rt△ABC中,AB=AC,A=90°,点D在BC上,;M为BC中点,请判断的形状,并说明你的理由。
解:∵Rt△ABC为等腰直角三角形,且M为BC的中点
∴提示作出底边BC上的高
∴连结AM,则
又AM平分BAC,∴B=EAM
∴FM=EM,∴△MFE为等腰三角形
但注意到FMB=AME
∴可证FME=90°
∴△MEF为等腰直角三角形
例6. 已知一直角三角形两条直角边上的中线长分别为AE=5,,求其斜边AB的长。
解:直角三角形中,求边长或线段长,常常提示运用勾股定理。
如图所示,不妨设Rt△ACB中,C=90°,AC=b,BC=a
则
【模拟试题】
1. 如图所示,已知求A的度数。
2. 如图所示,已知AD是△ABC中BC边上的高,AE是CAF的平分线,AE=2AD,求ACB与B差的度数。
3. Rt△ABC中,C=90°,A=22.5°,D在AC上,DC=BC,于E,求证:AE=BE。
4. △ABC中,AD为BC边上的高,AD=BD,DE=CD,延长BE交AC于F,求证:BF为△ABC中AC边上的高。
5. △ABC中,ACB=90°,D为BC延长线上一点,CD:AB=1:2,若E为AB中点,B的平分线交DE于F,求证:BF=DF。
6. Rt△ABC中,D为AC中点,于E,求证:。
7. 如图所示,已知BD平分ABF,AD=CD,,求证:互补。
8. 如图所示,△ABC中,以AB、AC为边分别向三角形外作正△ABF和正△ACE。BE、CF相交于点O,连结OA,求证:OA平分EOF。
9. 如图所示,△ABC中,AD平分BAC,BE=EC,过点E作,交AC和AD、AB的延长线于H、F、G。求证:。
10. 折叠一张矩形纸片ABCD,先沿对角线BD折叠,再把AD折叠到BD上(如图所示),已知AB=2,BC=1,求第二次折叠的折痕DE的长。
【试题答案】
坐标几何
1. 第二象限
2. 坐标原点
3.
4. C(-a,-b)
5. (-3,-2)
6. 答案不唯一,只要使点符合,,y为任意实数均可以。
7. (1)Rt△ABC,且∠B为直角;(2)
8.
(提示:设,则由PA=PB,得x=2,y=10)
三角形
1.
提示:设A=x,Rt△AFG中,A+G=90°,∴x=15°
2. 60°
3. 略
4. 提示:
5. 提示:连结CE,求证
6. 提示:连结BD,分别对运用勾股定理。
7. 提示:过D作BA的垂线,交BA的延长线于E,证明
8. 提示:过A分别向CF、BE作垂线,垂足分别为M、N
证明全等的一对三角形:△AFC与△ABE对应边上的高相等。
9. 提示:过B作AC的平行线交GH于N
证明,则AC=AH+HC=AB+BG+CH=AB+2BG
10.
提示:设AE=x,则,在Rt△BEF中,运用勾股定理解得,在Rt△ADE中,
PAGE
1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
