一元一次不等式组(浙江省温州市瑞安市)
文档属性
| 名称 | 一元一次不等式组(浙江省温州市瑞安市) |

|
|
| 格式 | rar | ||
| 文件大小 | 119.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-07-05 20:56:00 | ||
图片预览








文档简介
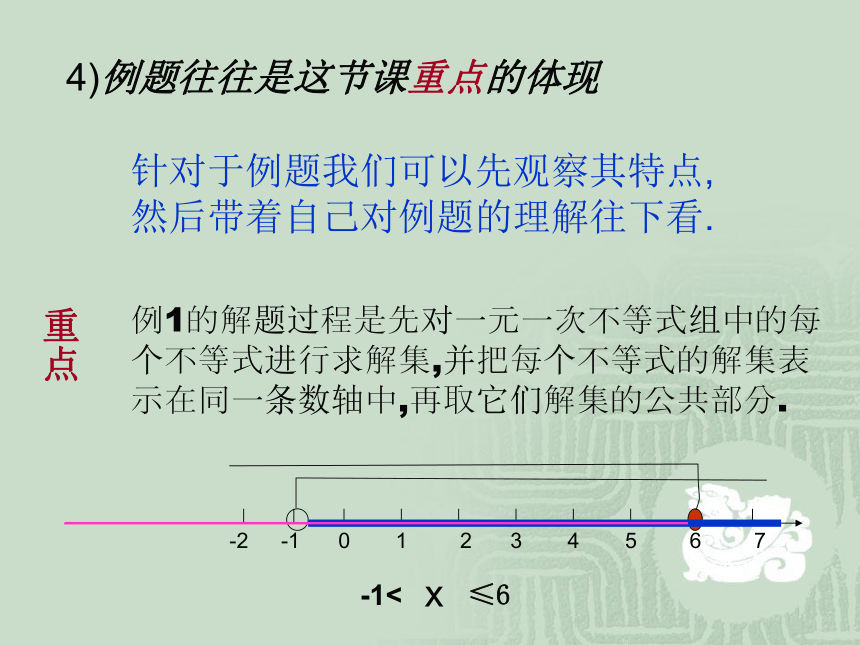
课件20张PPT。书中自有黄金屋书中自有颜如玉 “以书为本,自主学习”方法的探索以课题<一元一次不等式组>为例课题往往是知识精髓的提炼(一)在自主学习之前先要对课题进行联想与假想课题<一元一次不等式组>联想由“一元一次不等式”字眼想到的:什么叫一元一次不等式.什么叫一元一次不等式的解集.在数轴上如何表示一元一次不等式的解集.如 2x+4<6如 x<1由“组”字联想到的:二元一次方程组.什么叫二元一次方程组的解同时满足二元一次方程组中各个方程的解┅┅y=x+100的解x+y=200的解假想什么叫一元一次不等式组?与一元一次不等式有何关系?怎么去解一个一元一次不等式组?如何表示一元一次不等式组的解?(二)提纲1)一元一次不等式组的概念.表示的方法与二元一次方程组一样,都是用大括号括起来.3)一元一次不等式组解集的概念.4)例题往往是这节课重点的体现针对于例题我们可以先观察其特点,然后带着自己对例题的理解往下看.请回头理解一元一次不等式组解集的概念与二元一次方程组解的意义相类似
针对例1归纳解一元一次不等式组一般步骤:分别解出不等式组中的每个一元一次不等式的解集,1)2)把每个一元一次不等式的解集表示在同一条数轴上.3)请写出在数轴上能直观看到的公共部分的解集.在学习例2之前,根据自已对例1理解的基础上,自己可以先尝试着去求解一下.因为各一元一次不等式的解集在数轴上没有公共部分,所以无解.再次回头理解一下一元一次不等式组解集概念的补充部分.深1度思考一元一次不等式组的概念中的“几个”是什么意思,书本中就给我们两个一元一次不等式构成不等式组,那一个或三个或三个以上的一元一次不等式构成的还算一元一次不等式组吗?那其解集又是如何求解的呢?如:下列形式也是叫一元一次不等式组吗?为什么?在例1的一元一次不等式组中,我若改变其中一个不等号方向,它的解集有何变化?如作下面的变化:在例2当中我们可不可以也有同样的变化,情况将又会是怎样?可以尝试一下.如:X>回归生活当我们学习完这节课之后,回到每节课都有节前题的问题当中去,用我们今天所自学的知识尝试着去解决一下.小结:自主学习的方法:对课题有充分的联想与假想学习过程要列提纲重新回头对你列的提纲作深1度的思考尝试知识的应用----------回归生活希望同学们有个好的学习习惯!谢谢!
针对例1归纳解一元一次不等式组一般步骤:分别解出不等式组中的每个一元一次不等式的解集,1)2)把每个一元一次不等式的解集表示在同一条数轴上.3)请写出在数轴上能直观看到的公共部分的解集.在学习例2之前,根据自已对例1理解的基础上,自己可以先尝试着去求解一下.因为各一元一次不等式的解集在数轴上没有公共部分,所以无解.再次回头理解一下一元一次不等式组解集概念的补充部分.深1度思考一元一次不等式组的概念中的“几个”是什么意思,书本中就给我们两个一元一次不等式构成不等式组,那一个或三个或三个以上的一元一次不等式构成的还算一元一次不等式组吗?那其解集又是如何求解的呢?如:下列形式也是叫一元一次不等式组吗?为什么?在例1的一元一次不等式组中,我若改变其中一个不等号方向,它的解集有何变化?如作下面的变化:在例2当中我们可不可以也有同样的变化,情况将又会是怎样?可以尝试一下.如:X>回归生活当我们学习完这节课之后,回到每节课都有节前题的问题当中去,用我们今天所自学的知识尝试着去解决一下.小结:自主学习的方法:对课题有充分的联想与假想学习过程要列提纲重新回头对你列的提纲作深1度的思考尝试知识的应用----------回归生活希望同学们有个好的学习习惯!谢谢!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
