2.4二次函数的应用(1)
图片预览






文档简介
课件19张PPT。2.4 二次函数的应用⑴浙教版九年级上册第二章二次函数二次函数的解析式:1.一般式 y=ax2 +bx + c (a ? 0)二次函数的图象: 一条抛物线抛物线的形状,大小,开口方向完全由_____来决定.当a的绝对相等时,其形状完全相同,当a的绝对值越大,
则开口越小,反之成立.a2.顶点式3.交点式y = a(x+m)2 +ky=a(x- x1)(x- x2 ) (a ? 0)(两根式) y=ax2+bx+c当a>0时,抛物线的开口向上,顶点是抛物线上的最低点,有最小值。
当a<0时,抛物线的开口向下,顶点是抛物线上的最高点,有最大值。求二次函数的最值的方法有哪些?回顾与练习1、求下列二次函数的最大值或最小值:
⑴ y=-x2+58x-112; ⑵ y=-x2+4x解: ⑴配方得: y=-(x-29)2+729所以:当x=29时,y 达到最大值为729又因为: -1<0,则:图像开口向下,⑵ -1<0,
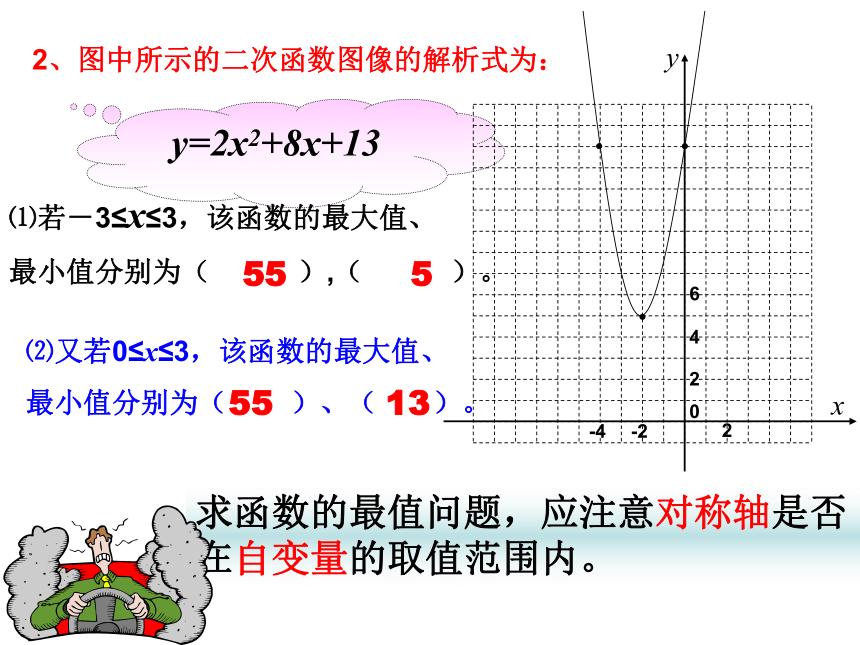
则:图像开口向下,函数有最大值所以由求最值公式可知,当x=2时, y达到最大值为4.最值要看图象的最高点或最低点2、图中所示的二次函数图像的解析式为:
y=2x2+8x+13⑴若-3≤x≤3,该函数的最大值、
最小值分别为( ),( )。 ⑵又若0≤x≤3,该函数的最大值、
最小值分别为( )、( )。55 555 13问题1:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?分析:利润=(每件商品所获利润)× (销售件数) 解:设每个涨价x元, 那么(3)销售量可以表示为(1)销售价可以表示为(50+x)元(500-10x) 个
(2)一个商品所获利润可以表示为(50+x-40)元(4)共获利润可以表示为(50+x-40)(500-10x)元情景建模问题:问题2、用长为8米的铝合金制成如图窗框,问窗框的宽和高各为多少米时,窗户的透光面积最大?最大面积是多少?解:设窗框的一边长为x米,
则另一边的长为(4-x)米,又令该窗框的透光面积为y米2,那么:y= x(4-x)且0< x<4又有:-1<0,
则:该函数的图像开口向下,故函数有最大值而图像的对称轴为直线x=2,且0< 2<4即:y=-x2+4x所以由求最值公式可知,当 x=2时,该函数达到最大值为4.答:该窗框的宽和高相等,都为2米时透光面积达到最大的4米2
问题3 用8m长的铝合金型材做一个形状如图所示的矩形窗框.应做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?问题4:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。 解: (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
∴ S=x(24-4x)
=-4x2+24 x (0∴ 0<24-4x ≤8 4≤x<6∴当x=4m时,S最大值=32 平方米练习感悟⑴数据(常量、变量)提取;⑵自变量、应变量识别;⑶构建函数解析式,并求出自变量的取值范围;⑷利用函数(或图像)的性质求最大(或最小)值。例1.如图窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形。如果制作一个窗户边框的材料的总长度为6米,那么如何设计这个窗户边框的尺寸,才能使窗户的透光面积最大(结果精确到0.01米)?XyDCABGHFE106解:设花园的面积为y
则 y=60-x2 -(10-x)(6-x)=-2x2 + 16x(0试一试
如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?PQD河北省赵县的赵州桥的桥拱是抛物线型,建立如图所
示的坐标系,其函数的表达式为y= - x2 , 当水位线在AB位
置时,水面宽 AB = 30米,这时水面离桥顶的高度h是( )
A、5米 B、6米; C、8米; D、9米做一做1.已知直角三角形的两直角边的和为2,求斜边长可能达到的最小值,以及当斜边长达到最小值时两条直角边的长分别为多少? 2 炮弹从炮口射出后,飞行的高度h(m)与飞行时间t(s)之间的函数关系式是h=V0tsinα-5t2,其中V0是炮弹发射的初速度,α是炮弹的发射角,当V0=300(m/s), α=30?时,炮弹飞行的最大高度是 m.
?
1125做一做 3.小张在某次投篮中,球的运动路线是抛物线
的一部分(如图),若命中篮圈中心,则他与篮底的距离l以及投篮时手离地面的高度分别是多少?做一做这节课你有什么收获和体会?
则开口越小,反之成立.a2.顶点式3.交点式y = a(x+m)2 +ky=a(x- x1)(x- x2 ) (a ? 0)(两根式) y=ax2+bx+c当a>0时,抛物线的开口向上,顶点是抛物线上的最低点,有最小值。
当a<0时,抛物线的开口向下,顶点是抛物线上的最高点,有最大值。求二次函数的最值的方法有哪些?回顾与练习1、求下列二次函数的最大值或最小值:
⑴ y=-x2+58x-112; ⑵ y=-x2+4x解: ⑴配方得: y=-(x-29)2+729所以:当x=29时,y 达到最大值为729又因为: -1<0,则:图像开口向下,⑵ -1<0,
则:图像开口向下,函数有最大值所以由求最值公式可知,当x=2时, y达到最大值为4.最值要看图象的最高点或最低点2、图中所示的二次函数图像的解析式为:
y=2x2+8x+13⑴若-3≤x≤3,该函数的最大值、
最小值分别为( ),( )。 ⑵又若0≤x≤3,该函数的最大值、
最小值分别为( )、( )。55 555 13问题1:某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?分析:利润=(每件商品所获利润)× (销售件数) 解:设每个涨价x元, 那么(3)销售量可以表示为(1)销售价可以表示为(50+x)元(500-10x) 个
(2)一个商品所获利润可以表示为(50+x-40)元(4)共获利润可以表示为(50+x-40)(500-10x)元情景建模问题:问题2、用长为8米的铝合金制成如图窗框,问窗框的宽和高各为多少米时,窗户的透光面积最大?最大面积是多少?解:设窗框的一边长为x米,
则另一边的长为(4-x)米,又令该窗框的透光面积为y米2,那么:y= x(4-x)且0< x<4又有:-1<0,
则:该函数的图像开口向下,故函数有最大值而图像的对称轴为直线x=2,且0< 2<4即:y=-x2+4x所以由求最值公式可知,当 x=2时,该函数达到最大值为4.答:该窗框的宽和高相等,都为2米时透光面积达到最大的4米2
问题3 用8m长的铝合金型材做一个形状如图所示的矩形窗框.应做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?问题4:如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积。 解: (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
∴ S=x(24-4x)
=-4x2+24 x (0
则 y=60-x2 -(10-x)(6-x)=-2x2 + 16x(0
如图,在ΔABC中,AB=8cm,BC=6cm,∠B=90°,
点P从点A开始沿AB边向点B以2厘米/秒的速度移动,
点Q从点B开始沿BC边向点C以1厘米/秒的速度
移动,如果P,Q分别从A,B同时出发,
几秒后ΔPBQ的面积最大?
最大面积是多少?PQD河北省赵县的赵州桥的桥拱是抛物线型,建立如图所
示的坐标系,其函数的表达式为y= - x2 , 当水位线在AB位
置时,水面宽 AB = 30米,这时水面离桥顶的高度h是( )
A、5米 B、6米; C、8米; D、9米做一做1.已知直角三角形的两直角边的和为2,求斜边长可能达到的最小值,以及当斜边长达到最小值时两条直角边的长分别为多少? 2 炮弹从炮口射出后,飞行的高度h(m)与飞行时间t(s)之间的函数关系式是h=V0tsinα-5t2,其中V0是炮弹发射的初速度,α是炮弹的发射角,当V0=300(m/s), α=30?时,炮弹飞行的最大高度是 m.
?
1125做一做 3.小张在某次投篮中,球的运动路线是抛物线
的一部分(如图),若命中篮圈中心,则他与篮底的距离l以及投篮时手离地面的高度分别是多少?做一做这节课你有什么收获和体会?
同课章节目录
