第二章 直线与圆的位置关系---切线的判定专项训练(含解析)
文档属性
| 名称 | 第二章 直线与圆的位置关系---切线的判定专项训练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 21:39:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
切线的判定专项训练(1)
夯实基础,稳扎稳打
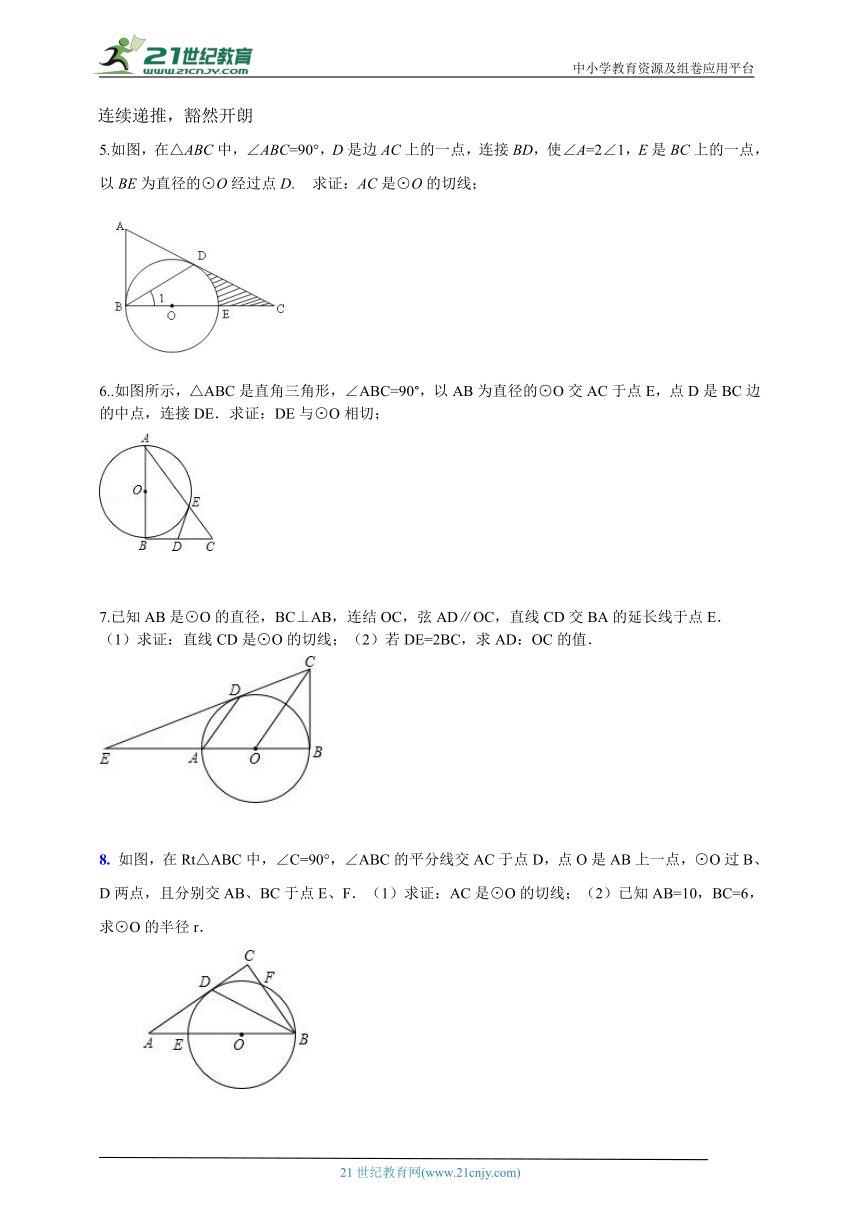
1.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
求证:CD是⊙O的切线;
2.如图,是的直径,是上一点,在的延长线上,且.
证:是的切线;
3.如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若∠DAC=∠BAC,且点D在⊙O的外部,求证:直线AD是⊙O的切线.
4.如图,已知AB、AC分别为⊙O的直径和弦,D为 弧BC的中点,DE⊥AC于E.求证:DE是⊙O的切线.[c*om~] 连续递推,豁然开朗
5.如图,在△ABC中,∠ ( http: / / www.21cnjy.com )ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.【来求证:AC是⊙O的切线;
6..如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE.求证:DE与⊙O相切;
7.已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
(1)求证:直线CD是⊙O的切线;(2)若DE=2BC,求AD:OC的值.
8. 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.(1)求证:AC是⊙O的切线;(2)已知AB=10,BC=6,求⊙O的半径r.
思维拓展,更上一层
9 .如图,,点在上,过点,分别与、交于、,过作于.求证:是的切线;若与相切于点,的半径为,,求长.
10.如图,在Rt△ABC中,∠BAC=90°,D为BC上的一点,以AD为直径的 交AB于E,连接CE交 于G,连接DG,∠ACB=∠EGD.
(1)证明:BC与 相切;
(2)若BD=2,CD=6,求 的直径AD;(3)在(2)的条件下,求EC.
11.如图,与等边的边AC,AB分别交于点D,E,AE是直径,过点D作于点F.(1)求证:DF是的切线;(2)连接EF,当EF是的切线时,求半径r与等边边长a的比值.
12 . 如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过 点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD。(1) 判断直线PC与圆O的位置关系,并说明理由:(2) 若AB=9,BC=6,求PC长。
切线的判定专项训练(2)
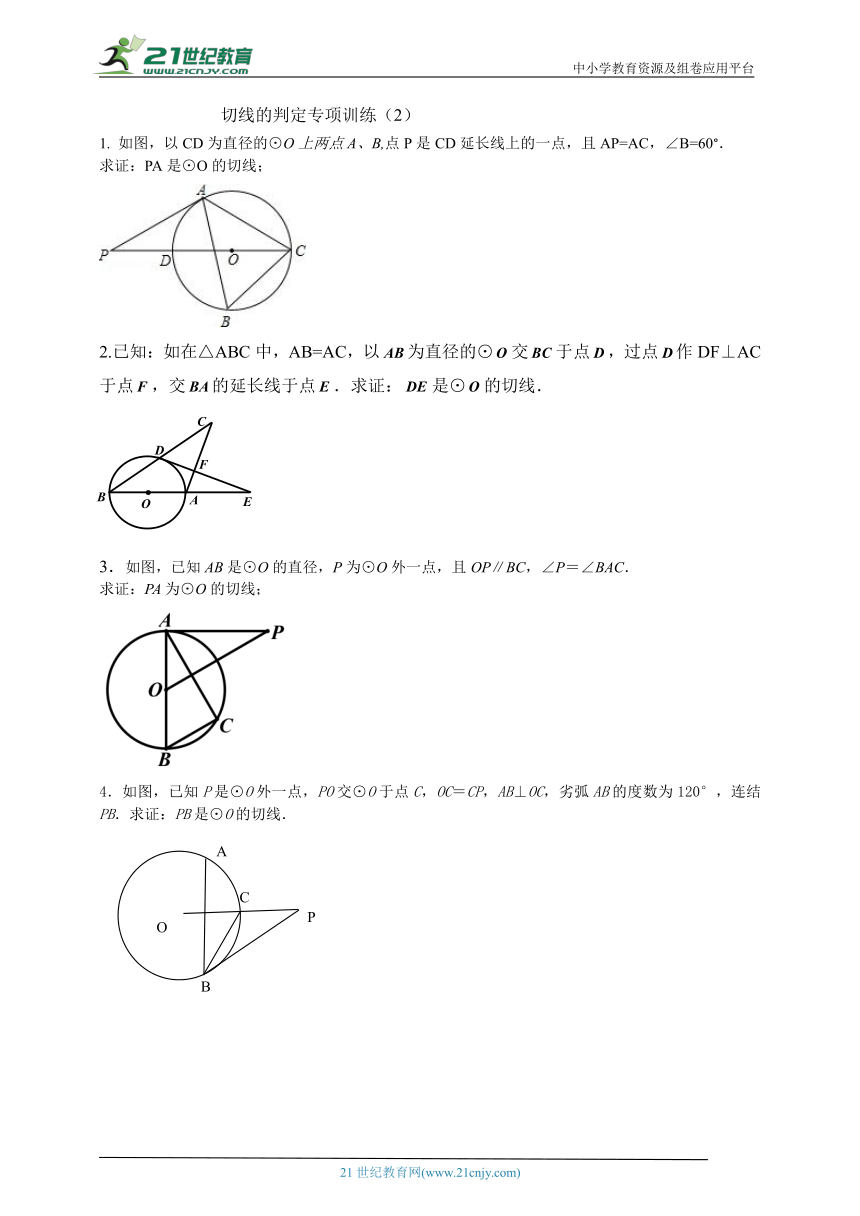
1. 如图,以CD为直径的⊙O上两点A、B,点P是CD延长线上的一点,且AP=AC,∠B=60°.
求证:PA是⊙O的切线;
2.已知:如在△ABC中,AB=AC,以为直径的⊙交于点,过点作DF⊥AC于点,交的延长线于点.求证:是⊙的切线.
3.如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
求证:PA为⊙O的切线;
4.如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP,AB⊥OC,劣弧AB的度数为120°,连结PB.求证:PB是⊙O的切线.
连续递推,豁然开朗
5..如图所示.P是⊙O外一点.PA是⊙O的切线,点A是切点.B是⊙O上一点.
且PA = PB,连接AO、BO、PO、AB,并延长BO与切线PA相交于点C.
求证:PB是⊙O的切线 ;[来源%:中国教育
6.在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB与点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F,连接OC、FC.
(1)求证:CE是⊙O的切线;(2)若FC∥AB,求证:四边形AOCF是菱形.
7.如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.(1)求证:CT为⊙O的切线;(2)若⊙O半径为2,CT=,求AD的长.
8.已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;(2)若DE=6cm,AE=3cm,求⊙O的半径.
思维拓展,更上一层
9.如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q。(1)在线段PQ上取一点D,使DQ=DC,连接DC,判断CD与⊙O的位置关系,说明理由。(2)若cosB=,BP=6,AP=1,求QC的长
10.如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=,BE=2.求证:(1)四边形FADC是菱形;(2)FC是⊙O的切线.
11.如图,AB是⊙O的直径,AD平分∠BAC,点C,D在⊙O上,过点D作DE⊥AC,交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)若CE=2,DE=4,求AD长.
12.如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=0.25,求BN的长.
切线的判定专项训练(1)参考答案
1.证明:连接OC.∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.
∵OA=OC,∴∠2=∠A=30°.∴∠OCD=90°.∴CD是⊙O的切线.
2.证明:如图,连接.
∵是的直径,是上一点,∴,即.
∵,,∴,
∴,即,∴是的切线.
3.证明 : ∵半径OC垂直于弦AB,∵AC弧=BC弧,∴∠AOC=2∠BA C,∵∠DAC=∠BAC,∴∠AOC=∠BAD,∵∠AOC+∠OAE=90°,∴∠BAD+∠OAE=90°,∴OA⊥AD,∴AD为⊙O的切线.
4. (1)证明:连接OD,BC。
∵AB为⊙O的直径,∴BC⊥AC。[ ∵DE⊥AC,∴BC//DE。%p.#co*&m
∵D为弧BC的中点,∴OD⊥BC ∴OD⊥DE[~p.c∴DE是⊙O的切线。#p.com*]
%源#:@step.c*om&]
5.证明:如图,连接OD ∵,∴,∴∠,
∵,∴,∠ABC=90°,∴,∵OD为半径,∴AC是⊙O的切线;
6.
解:(1)证明:连接OE,BE,∵AB是直径.∴BE⊥AC.∵D是BC的中点,∴DC=DB.∴∠DBE=∠DEB.又OE=OB,∴∠OBE=∠OEB.∴∠DBE+∠OBE=∠DEB+∠OEB.即∠ABD=∠OED.但∠ABC=90°,∴∠OED=90°.∴DE是⊙O的切线.[c*om~]
7.【解析】1)证明:连结DO.∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD
又∵OA=OD,∴∠DAO=∠ADO,∴∠COD=∠COB.
在△COD和△COB中,,∴△COD≌△COB(SAS)
∴∠CDO=∠CBO=90°.又∵点D在⊙O上,∴CD是⊙O的切线.
(2)解:∵△COD≌△COB.∴CD=CB.∵DE=2BC,∴ED=2CD.
∵AD∥OC,∴△EDA∽△ECO.∴.
8(1)证明:连接OD。 ∵OB=OD,∴∠OBD=∠ODB。
∵BD平分∠ABC,∴∠ABD=∠DBC∴∠ODB=∠DBC。∴OD∥BC。
又∵∠C=90°,∴∠ADO=90°。∴AC⊥OD,即AC是⊙O的切线。
(2)解:由(1)知,OD∥BC,∴△AOD∽△ABC。
∴,即。解得,即⊙O的半径r为。
9.证明:连接,∵,∴,∵,∴,
∴,∴,∵,∴,则为圆的切线;
解:连接,∵与圆相切,∴,
∴,且,
∴四边形为边长为的正方形,
设,则有,,
在中,利用勾股定理得:,即,
解得:,则.
10.(1)证明:∵ , ,
∴ ,又∵ ,∴ ,∴ ,
∴ ,又∵ 为半径,∴ 与 相切.
(2)解:由(1)知 ,又 ,
∴ ,∴ ,又 , ,∴ .
(3)解:由(2)知,在 中, ,
连接 ,如图,
∵ 是直径,∴ ,∴ ,又 ,
∴ ,∴ ,即 ,∴ ,
∴ ,
在 中, ,
在 中, .
11(1)证明:连接OD,如图所示:
∵∠DAO=60°,OD=OA,∴△DOA是等边三角形,∴∠ODA=∠C=60°,∴OD∥BC,
又∵∠DFC=90°,∴∠ODF=90°,∴OD⊥DF,即DF是⊙O的切线;
(2)解:设半径为r,等边△ABC的边长为a,
由(1)可知:AD=r,则CD=a-r,BE=a-2r
在Rt△CFD中,∠C=60°,CD=a-r,∴CF=(a r),∴BF=a- (a r),
又∵EF是⊙O的切线,
∴△FEB是直角三角形,且∠B=60°,∠EFB=30°,∴BF=2BE,∴a-(a-r)=2(a-2r),
解得:a=3r,即r=a,∴⊙O的半径r与等边△ABC的边长a之间的数量关系为:r=a.
12, 解法一:(1) 直线PC与圆O相切。
如图,连接CO并延长,交圆O于点N,连接BN。
∵AB//CD,∴BAC=ACD。
∵BAC=BNC,∴BNC=ACD。
∵BCP=ACD,∴BNC=BCP。
∵CN是圆O的直径,∴CBN=90。
∴BNCBCN=90,∴BCPBCN=90。
∴PCO=90,即PCOC。
又点C在圆O上,∴直线PC与圆O相切。
(2) ∵AD是圆O的切线,∴ADOA,即OAD=90。
∵BC//AD,∴OMC=180OAD=90,即OMBC。
∴MC=MB。∴AB=AC。
在Rt△AMC中,AMC=90,AC=AB=9,MC= BC=3,
由勾股定理,得AM===6。
设圆O的半径为r。
在Rt△OMC中,OMC=90,OM=AMAO=6r,MC=3,OC=r,
由勾股定理,得OM 2MC 2=OC 2,即(6r)232=r2。解得r= 。
在△OMC和△OCP中, ∵OMC=OCP,MOC=COP,
∴△OMC~△OCP。∴ = ,即 EQ \F( 6 , ) = 。
∴PC= 。
解法二:(1) 直线PC与圆O相切。如图,连接OC。
∵AD是圆O的切线,∴ADOA,
即OAD=90。
∵BC//AD,∴OMC=180OAD=90,
即OMBC。
∴MC=MB。∴AB=AC。∴MAB=MAC。
∴BAC=2MAC。又∵MOC=2MAC,∴MOC=BAC。
∵AB//CD,∴BAC=ACD。∴MOC=ACD。又∵BCP=ACD,
∴MOC=BCP。∵MOCOCM=90,∴BCPOCM=90。
∴PCO=90,即PCOC。又∵点C在圆O上,∴直线PC与圆O相切。
(2) 在Rt△AMC中,AMC=90,AC=AB=9,MC= BC=3,
由勾股定理,得AM===6。
设圆O的半径为r。
在Rt△OMC中,OMC=90,OM=AMAO=6r,MC=3,OC=r,
由勾股定理,得OM 2MC 2=OC 2,即(6r)232=r2。解得r= 。
在△OMC和△OCP中,∵OMC=OCP,MOC=COP,
∴△OMC~△OCP,∴ = ,即 EQ \F( 6 , ) = 。
∴PC= 。
切线的判定专项训练(2)参考答案
(1)证明:连接OA,∵∠B=60°,∴∠AOC=2∠B=120°,又∵OA=OC,∴∠OAC=∠OCA=30°,又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=∠AOC﹣∠P=90°,∴OA⊥PA,∴PA是⊙O的切线.
2.解: 连结, ∥ 是⊙的切线
#源:中*@教&网%]
3.
.【解】(1)设AC与OP相交于点H
∵AB是直径,∴AC⊥BC,∠BAC+∠B=90°
∵OP∥BC,∴OP⊥AC,∠AOP=∠B
∵∠P=∠BAC∴∠P+∠AOP=90°,于是∠OAP=90°∴PA为⊙O的切线
4.证明:连结OB.
∵弦AB⊥OC,劣弧AB的度数为120°,∴∠COB=60°.
又∵OC=OB,∴△OBC是正三角形∴∠OBC=∠OCB=60°
∵BC=CP,∴∠CBP=∠CPB.∴∠CBP=30°.
∴∠OBP=∠CBP+∠OBC=90°.∴OB⊥BP.
∵点B在⊙O上,∴PB是⊙O的切线.
5..证明: ∵PA=PB,AO=BO,PO=PO∴△APO≌△BPO
∵ PA是⊙O的切线 ∴∠PAO=90°=∠PBO ∴PB是⊙O的切线[
6.解:(1)由翻折可知,∠FAC=∠OAC, ∠E=∠ADC=90°,
∵OA=OC,[∴∠OAC=∠OCA,∴∠FAC=∠OCA,∴OC∥AE,[来%@源:中教网#~&]
∴∠OCE=90°,即OC⊥CE. ∴CE是⊙O的切线.
(2)∵FC∥AB,OC∥AF,[∴四边形AOCF是平行四边形.[来源:中~*国教@
%∵OA=OC,∴ AOCF是菱形.
7解答:(1)证明:连接OT,∵OA=OT,∴∠OAT=∠OTA,又∵AT平分∠BAD,
∴∠DAT=∠OAT,∴∠DAT=∠OTA,∴OT∥AC,又∵CT⊥AC,∴CT⊥OT,
∴CT为⊙O的切线;(2)解:过O作OE⊥AD于E,则E为AD中点,
又∵CT⊥AC,∴OE∥CT,∴四边形OTCE为矩形,∵CT=,∴OE=,
又∵OA=2,∴在Rt△OAE中,,
∴AD=2AE=2.
8.解答:(1)证明:连接OD.∵OA=OD,∴∠OAD=∠ODA.∵∠OAD=∠DAE,
∴∠ODA=∠DAE.∴DO∥MN.∵DE⊥MN,∴∠ODE=∠DEM=90°.
即OD⊥DE.∵D在⊙O上,∴DE是⊙O的切线.(2)解:∵∠AED=90°,DE=6,AE=3,
∴.连接CD.∵AC是⊙O的直径,
∴∠ADC=∠AED=90°.∵∠CAD=∠DAE,∴△ACD∽△ADE.∴.
9.解:(1)CD是⊙O的切线,
理由如下:连接OC,∵OC=OB,∴∠B=∠1.又∵DC=DQ,∴∠Q=∠2
∵PQ⊥AB,∴∠QPB=90°∴∠B+∠Q=90°∴∠1+∠2=90°∴∠DCO=∠QCB-(∠1+∠2)=180°-90°,
∴OC⊥DC,∵OC是⊙O的半径∴CD是⊙O的切线
(2)连接AC,∵AB是⊙O的直径,∴∠ACB=90°.
在Rt△ABC中,
BC=ABcosB=(AP+BP) cosB=(1+6)×=.
在Rt△BPQ中BQ===10 ∴QC=BQ-BC=10==
10.解答:证明:(1)连接OC,∵AB是⊙O的直径,CD⊥AB,∴CE=DE=2,
设OC=x,∵BE=2,∴OE=x-2,
在Rt△OCE中,OC2=OE2+CE2,∴x2=(x-2)2+(2)2,解得:x=4,
∴OA=OC=4,OE=2,∴AE=6,
在Rt△AED中,AD==4,∴AD=CD,
∵AF是⊙O切线,∴AF⊥AB,∵CD⊥AB,∴AF∥CD,
∵CF∥AD,∴四边形FADC是平行四边形,∴ FADC是菱形;
(2)连接OF,∵四边形FADC是菱形,∴FA=FC,
在△AFO和△CFO中,,∴△AFO≌△CFO(SSS),∴∠FCO=∠FAO=90°,即OC⊥FC,
∵点C在⊙O上,∴FC是⊙O的切线.
11(1)证明:如下图,连接OD,
∵DE⊥AC,∴∠DEA=90°,∵AD平分∠BAC,∴∠EAD=∠DAB,
∵OA=OD,∴∠OAD=∠ODA,∴∠EAD=∠ADO,∴AE∥OD,
∴∠ODE+∠AED=180°,∴∠ODE=180°-∠AED=90°,
∵OD是⊙O的半径,∴DE是⊙O的切线;
(2)解:如下图,连接DB,CD,
∵AB是⊙O的直径,∴∠ADB=90°,∴∠DAB+∠B=90°,
∵∠E=90°,∴∠EAD+∠EDA=90°,
∵∠EAD=∠DAB,∴∠B=∠EDA,
∵四边形ABDC是⊙O的内接四边形,∴∠ACD+∠B=180°,
∵∠ACD+∠ECD=180°,∴∠B=∠ECD,∴∠ECD=∠EDA,
∵∠E=∠E,∴△ECD∽△EDA,∴ ,∴,∴,
∴
12解答: (1)证明:∵△BCO中,BO=CO,∴∠B=∠BCO,在Rt△BCE中,∠2+∠B=90°,又∵∠1=∠2,∴∠1+∠BCO=90°,即∠FCO=90°,∴CF是⊙O的切线;(2)证明:∵AB是⊙O直径,∴∠ACB=∠FCO=90°,∴∠ACB﹣∠BCO=∠FCO﹣∠BCO,即∠3=∠1,∴∠3=∠2,∵∠4=∠D,∴△ACM∽△DCN;(3)解:∵⊙O的半径为4,即AO=CO=BO=4,在Rt△COE中,cos∠BOC=0.25,∴OE=CO cos∠BOC=4×0.25=1,由此可得:BE=3,AE=5,由勾股定理可得:CE===,AC===2,BC===2,∵AB是⊙O直径,AB⊥CD,∴由垂径定理得:CD=2CE=2,∵△ACM∽△DCN,∴=,∵点M是CO的中点,CM=AO=×4=2,∴CN===,∴BN=BC﹣CN=2﹣=.
C
E
A
O
B
D
A
B
C
D
O
M
P
A
C
PP
B
O
A
B
C
D
O
M
P
N
A
B
C
D
O
M
P
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
切线的判定专项训练(1)
夯实基础,稳扎稳打
1.如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
求证:CD是⊙O的切线;
2.如图,是的直径,是上一点,在的延长线上,且.
证:是的切线;
3.如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.若∠DAC=∠BAC,且点D在⊙O的外部,求证:直线AD是⊙O的切线.
4.如图,已知AB、AC分别为⊙O的直径和弦,D为 弧BC的中点,DE⊥AC于E.求证:DE是⊙O的切线.[c*om~] 连续递推,豁然开朗
5.如图,在△ABC中,∠ ( http: / / www.21cnjy.com )ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.【来求证:AC是⊙O的切线;
6..如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE.求证:DE与⊙O相切;
7.已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
(1)求证:直线CD是⊙O的切线;(2)若DE=2BC,求AD:OC的值.
8. 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.(1)求证:AC是⊙O的切线;(2)已知AB=10,BC=6,求⊙O的半径r.
思维拓展,更上一层
9 .如图,,点在上,过点,分别与、交于、,过作于.求证:是的切线;若与相切于点,的半径为,,求长.
10.如图,在Rt△ABC中,∠BAC=90°,D为BC上的一点,以AD为直径的 交AB于E,连接CE交 于G,连接DG,∠ACB=∠EGD.
(1)证明:BC与 相切;
(2)若BD=2,CD=6,求 的直径AD;(3)在(2)的条件下,求EC.
11.如图,与等边的边AC,AB分别交于点D,E,AE是直径,过点D作于点F.(1)求证:DF是的切线;(2)连接EF,当EF是的切线时,求半径r与等边边长a的比值.
12 . 如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过 点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD。(1) 判断直线PC与圆O的位置关系,并说明理由:(2) 若AB=9,BC=6,求PC长。
切线的判定专项训练(2)
1. 如图,以CD为直径的⊙O上两点A、B,点P是CD延长线上的一点,且AP=AC,∠B=60°.
求证:PA是⊙O的切线;
2.已知:如在△ABC中,AB=AC,以为直径的⊙交于点,过点作DF⊥AC于点,交的延长线于点.求证:是⊙的切线.
3.如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
求证:PA为⊙O的切线;
4.如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP,AB⊥OC,劣弧AB的度数为120°,连结PB.求证:PB是⊙O的切线.
连续递推,豁然开朗
5..如图所示.P是⊙O外一点.PA是⊙O的切线,点A是切点.B是⊙O上一点.
且PA = PB,连接AO、BO、PO、AB,并延长BO与切线PA相交于点C.
求证:PB是⊙O的切线 ;[来源%:中国教育
6.在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB与点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F,连接OC、FC.
(1)求证:CE是⊙O的切线;(2)若FC∥AB,求证:四边形AOCF是菱形.
7.如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.(1)求证:CT为⊙O的切线;(2)若⊙O半径为2,CT=,求AD的长.
8.已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;(2)若DE=6cm,AE=3cm,求⊙O的半径.
思维拓展,更上一层
9.如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q。(1)在线段PQ上取一点D,使DQ=DC,连接DC,判断CD与⊙O的位置关系,说明理由。(2)若cosB=,BP=6,AP=1,求QC的长
10.如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=,BE=2.求证:(1)四边形FADC是菱形;(2)FC是⊙O的切线.
11.如图,AB是⊙O的直径,AD平分∠BAC,点C,D在⊙O上,过点D作DE⊥AC,交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)若CE=2,DE=4,求AD长.
12.如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=0.25,求BN的长.
切线的判定专项训练(1)参考答案
1.证明:连接OC.∵AC=CD,∠ACD=120°,∴∠A=∠D=30°.
∵OA=OC,∴∠2=∠A=30°.∴∠OCD=90°.∴CD是⊙O的切线.
2.证明:如图,连接.
∵是的直径,是上一点,∴,即.
∵,,∴,
∴,即,∴是的切线.
3.证明 : ∵半径OC垂直于弦AB,∵AC弧=BC弧,∴∠AOC=2∠BA C,∵∠DAC=∠BAC,∴∠AOC=∠BAD,∵∠AOC+∠OAE=90°,∴∠BAD+∠OAE=90°,∴OA⊥AD,∴AD为⊙O的切线.
4. (1)证明:连接OD,BC。
∵AB为⊙O的直径,∴BC⊥AC。[ ∵DE⊥AC,∴BC//DE。%p.#co*&m
∵D为弧BC的中点,∴OD⊥BC ∴OD⊥DE[~p.c∴DE是⊙O的切线。#p.com*]
%源#:@step.c*om&]
5.证明:如图,连接OD ∵,∴,∴∠,
∵,∴,∠ABC=90°,∴,∵OD为半径,∴AC是⊙O的切线;
6.
解:(1)证明:连接OE,BE,∵AB是直径.∴BE⊥AC.∵D是BC的中点,∴DC=DB.∴∠DBE=∠DEB.又OE=OB,∴∠OBE=∠OEB.∴∠DBE+∠OBE=∠DEB+∠OEB.即∠ABD=∠OED.但∠ABC=90°,∴∠OED=90°.∴DE是⊙O的切线.[c*om~]
7.【解析】1)证明:连结DO.∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD
又∵OA=OD,∴∠DAO=∠ADO,∴∠COD=∠COB.
在△COD和△COB中,,∴△COD≌△COB(SAS)
∴∠CDO=∠CBO=90°.又∵点D在⊙O上,∴CD是⊙O的切线.
(2)解:∵△COD≌△COB.∴CD=CB.∵DE=2BC,∴ED=2CD.
∵AD∥OC,∴△EDA∽△ECO.∴.
8(1)证明:连接OD。 ∵OB=OD,∴∠OBD=∠ODB。
∵BD平分∠ABC,∴∠ABD=∠DBC∴∠ODB=∠DBC。∴OD∥BC。
又∵∠C=90°,∴∠ADO=90°。∴AC⊥OD,即AC是⊙O的切线。
(2)解:由(1)知,OD∥BC,∴△AOD∽△ABC。
∴,即。解得,即⊙O的半径r为。
9.证明:连接,∵,∴,∵,∴,
∴,∴,∵,∴,则为圆的切线;
解:连接,∵与圆相切,∴,
∴,且,
∴四边形为边长为的正方形,
设,则有,,
在中,利用勾股定理得:,即,
解得:,则.
10.(1)证明:∵ , ,
∴ ,又∵ ,∴ ,∴ ,
∴ ,又∵ 为半径,∴ 与 相切.
(2)解:由(1)知 ,又 ,
∴ ,∴ ,又 , ,∴ .
(3)解:由(2)知,在 中, ,
连接 ,如图,
∵ 是直径,∴ ,∴ ,又 ,
∴ ,∴ ,即 ,∴ ,
∴ ,
在 中, ,
在 中, .
11(1)证明:连接OD,如图所示:
∵∠DAO=60°,OD=OA,∴△DOA是等边三角形,∴∠ODA=∠C=60°,∴OD∥BC,
又∵∠DFC=90°,∴∠ODF=90°,∴OD⊥DF,即DF是⊙O的切线;
(2)解:设半径为r,等边△ABC的边长为a,
由(1)可知:AD=r,则CD=a-r,BE=a-2r
在Rt△CFD中,∠C=60°,CD=a-r,∴CF=(a r),∴BF=a- (a r),
又∵EF是⊙O的切线,
∴△FEB是直角三角形,且∠B=60°,∠EFB=30°,∴BF=2BE,∴a-(a-r)=2(a-2r),
解得:a=3r,即r=a,∴⊙O的半径r与等边△ABC的边长a之间的数量关系为:r=a.
12, 解法一:(1) 直线PC与圆O相切。
如图,连接CO并延长,交圆O于点N,连接BN。
∵AB//CD,∴BAC=ACD。
∵BAC=BNC,∴BNC=ACD。
∵BCP=ACD,∴BNC=BCP。
∵CN是圆O的直径,∴CBN=90。
∴BNCBCN=90,∴BCPBCN=90。
∴PCO=90,即PCOC。
又点C在圆O上,∴直线PC与圆O相切。
(2) ∵AD是圆O的切线,∴ADOA,即OAD=90。
∵BC//AD,∴OMC=180OAD=90,即OMBC。
∴MC=MB。∴AB=AC。
在Rt△AMC中,AMC=90,AC=AB=9,MC= BC=3,
由勾股定理,得AM===6。
设圆O的半径为r。
在Rt△OMC中,OMC=90,OM=AMAO=6r,MC=3,OC=r,
由勾股定理,得OM 2MC 2=OC 2,即(6r)232=r2。解得r= 。
在△OMC和△OCP中, ∵OMC=OCP,MOC=COP,
∴△OMC~△OCP。∴ = ,即 EQ \F( 6 , ) = 。
∴PC= 。
解法二:(1) 直线PC与圆O相切。如图,连接OC。
∵AD是圆O的切线,∴ADOA,
即OAD=90。
∵BC//AD,∴OMC=180OAD=90,
即OMBC。
∴MC=MB。∴AB=AC。∴MAB=MAC。
∴BAC=2MAC。又∵MOC=2MAC,∴MOC=BAC。
∵AB//CD,∴BAC=ACD。∴MOC=ACD。又∵BCP=ACD,
∴MOC=BCP。∵MOCOCM=90,∴BCPOCM=90。
∴PCO=90,即PCOC。又∵点C在圆O上,∴直线PC与圆O相切。
(2) 在Rt△AMC中,AMC=90,AC=AB=9,MC= BC=3,
由勾股定理,得AM===6。
设圆O的半径为r。
在Rt△OMC中,OMC=90,OM=AMAO=6r,MC=3,OC=r,
由勾股定理,得OM 2MC 2=OC 2,即(6r)232=r2。解得r= 。
在△OMC和△OCP中,∵OMC=OCP,MOC=COP,
∴△OMC~△OCP,∴ = ,即 EQ \F( 6 , ) = 。
∴PC= 。
切线的判定专项训练(2)参考答案
(1)证明:连接OA,∵∠B=60°,∴∠AOC=2∠B=120°,又∵OA=OC,∴∠OAC=∠OCA=30°,又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=∠AOC﹣∠P=90°,∴OA⊥PA,∴PA是⊙O的切线.
2.解: 连结, ∥ 是⊙的切线
#源:中*@教&网%]
3.
.【解】(1)设AC与OP相交于点H
∵AB是直径,∴AC⊥BC,∠BAC+∠B=90°
∵OP∥BC,∴OP⊥AC,∠AOP=∠B
∵∠P=∠BAC∴∠P+∠AOP=90°,于是∠OAP=90°∴PA为⊙O的切线
4.证明:连结OB.
∵弦AB⊥OC,劣弧AB的度数为120°,∴∠COB=60°.
又∵OC=OB,∴△OBC是正三角形∴∠OBC=∠OCB=60°
∵BC=CP,∴∠CBP=∠CPB.∴∠CBP=30°.
∴∠OBP=∠CBP+∠OBC=90°.∴OB⊥BP.
∵点B在⊙O上,∴PB是⊙O的切线.
5..证明: ∵PA=PB,AO=BO,PO=PO∴△APO≌△BPO
∵ PA是⊙O的切线 ∴∠PAO=90°=∠PBO ∴PB是⊙O的切线[
6.解:(1)由翻折可知,∠FAC=∠OAC, ∠E=∠ADC=90°,
∵OA=OC,[∴∠OAC=∠OCA,∴∠FAC=∠OCA,∴OC∥AE,[来%@源:中教网#~&]
∴∠OCE=90°,即OC⊥CE. ∴CE是⊙O的切线.
(2)∵FC∥AB,OC∥AF,[∴四边形AOCF是平行四边形.[来源:中~*国教@
%∵OA=OC,∴ AOCF是菱形.
7解答:(1)证明:连接OT,∵OA=OT,∴∠OAT=∠OTA,又∵AT平分∠BAD,
∴∠DAT=∠OAT,∴∠DAT=∠OTA,∴OT∥AC,又∵CT⊥AC,∴CT⊥OT,
∴CT为⊙O的切线;(2)解:过O作OE⊥AD于E,则E为AD中点,
又∵CT⊥AC,∴OE∥CT,∴四边形OTCE为矩形,∵CT=,∴OE=,
又∵OA=2,∴在Rt△OAE中,,
∴AD=2AE=2.
8.解答:(1)证明:连接OD.∵OA=OD,∴∠OAD=∠ODA.∵∠OAD=∠DAE,
∴∠ODA=∠DAE.∴DO∥MN.∵DE⊥MN,∴∠ODE=∠DEM=90°.
即OD⊥DE.∵D在⊙O上,∴DE是⊙O的切线.(2)解:∵∠AED=90°,DE=6,AE=3,
∴.连接CD.∵AC是⊙O的直径,
∴∠ADC=∠AED=90°.∵∠CAD=∠DAE,∴△ACD∽△ADE.∴.
9.解:(1)CD是⊙O的切线,
理由如下:连接OC,∵OC=OB,∴∠B=∠1.又∵DC=DQ,∴∠Q=∠2
∵PQ⊥AB,∴∠QPB=90°∴∠B+∠Q=90°∴∠1+∠2=90°∴∠DCO=∠QCB-(∠1+∠2)=180°-90°,
∴OC⊥DC,∵OC是⊙O的半径∴CD是⊙O的切线
(2)连接AC,∵AB是⊙O的直径,∴∠ACB=90°.
在Rt△ABC中,
BC=ABcosB=(AP+BP) cosB=(1+6)×=.
在Rt△BPQ中BQ===10 ∴QC=BQ-BC=10==
10.解答:证明:(1)连接OC,∵AB是⊙O的直径,CD⊥AB,∴CE=DE=2,
设OC=x,∵BE=2,∴OE=x-2,
在Rt△OCE中,OC2=OE2+CE2,∴x2=(x-2)2+(2)2,解得:x=4,
∴OA=OC=4,OE=2,∴AE=6,
在Rt△AED中,AD==4,∴AD=CD,
∵AF是⊙O切线,∴AF⊥AB,∵CD⊥AB,∴AF∥CD,
∵CF∥AD,∴四边形FADC是平行四边形,∴ FADC是菱形;
(2)连接OF,∵四边形FADC是菱形,∴FA=FC,
在△AFO和△CFO中,,∴△AFO≌△CFO(SSS),∴∠FCO=∠FAO=90°,即OC⊥FC,
∵点C在⊙O上,∴FC是⊙O的切线.
11(1)证明:如下图,连接OD,
∵DE⊥AC,∴∠DEA=90°,∵AD平分∠BAC,∴∠EAD=∠DAB,
∵OA=OD,∴∠OAD=∠ODA,∴∠EAD=∠ADO,∴AE∥OD,
∴∠ODE+∠AED=180°,∴∠ODE=180°-∠AED=90°,
∵OD是⊙O的半径,∴DE是⊙O的切线;
(2)解:如下图,连接DB,CD,
∵AB是⊙O的直径,∴∠ADB=90°,∴∠DAB+∠B=90°,
∵∠E=90°,∴∠EAD+∠EDA=90°,
∵∠EAD=∠DAB,∴∠B=∠EDA,
∵四边形ABDC是⊙O的内接四边形,∴∠ACD+∠B=180°,
∵∠ACD+∠ECD=180°,∴∠B=∠ECD,∴∠ECD=∠EDA,
∵∠E=∠E,∴△ECD∽△EDA,∴ ,∴,∴,
∴
12解答: (1)证明:∵△BCO中,BO=CO,∴∠B=∠BCO,在Rt△BCE中,∠2+∠B=90°,又∵∠1=∠2,∴∠1+∠BCO=90°,即∠FCO=90°,∴CF是⊙O的切线;(2)证明:∵AB是⊙O直径,∴∠ACB=∠FCO=90°,∴∠ACB﹣∠BCO=∠FCO﹣∠BCO,即∠3=∠1,∴∠3=∠2,∵∠4=∠D,∴△ACM∽△DCN;(3)解:∵⊙O的半径为4,即AO=CO=BO=4,在Rt△COE中,cos∠BOC=0.25,∴OE=CO cos∠BOC=4×0.25=1,由此可得:BE=3,AE=5,由勾股定理可得:CE===,AC===2,BC===2,∵AB是⊙O直径,AB⊥CD,∴由垂径定理得:CD=2CE=2,∵△ACM∽△DCN,∴=,∵点M是CO的中点,CM=AO=×4=2,∴CN===,∴BN=BC﹣CN=2﹣=.
C
E
A
O
B
D
A
B
C
D
O
M
P
A
C
PP
B
O
A
B
C
D
O
M
P
N
A
B
C
D
O
M
P
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
