第二章 和切线有关的线段长度计算 专项训练(含答案)
文档属性
| 名称 | 第二章 和切线有关的线段长度计算 专项训练(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 994.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
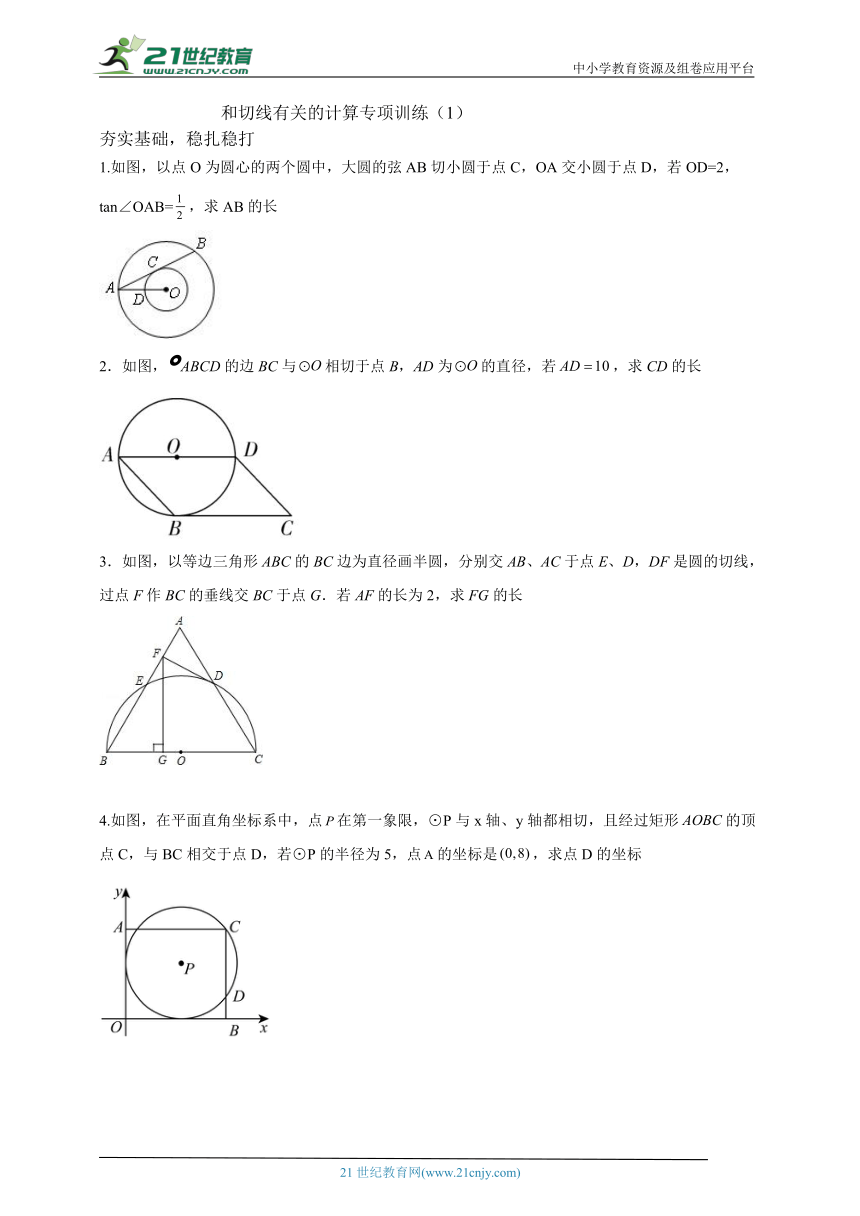
和切线有关的计算专项训练(1)
夯实基础,稳扎稳打
1.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=,求AB的长
2.如图,ABCD的边BC与相切于点B,AD为的直径,若,求CD的长
3.如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,求FG的长
4.如图,在平面直角坐标系中,点在第一象限,⊙P与x轴、y轴都相切,且经过矩形的顶点C,与BC相交于点D,若⊙P的半径为5,点的坐标是,求点D的坐标
连续递推,豁然开朗
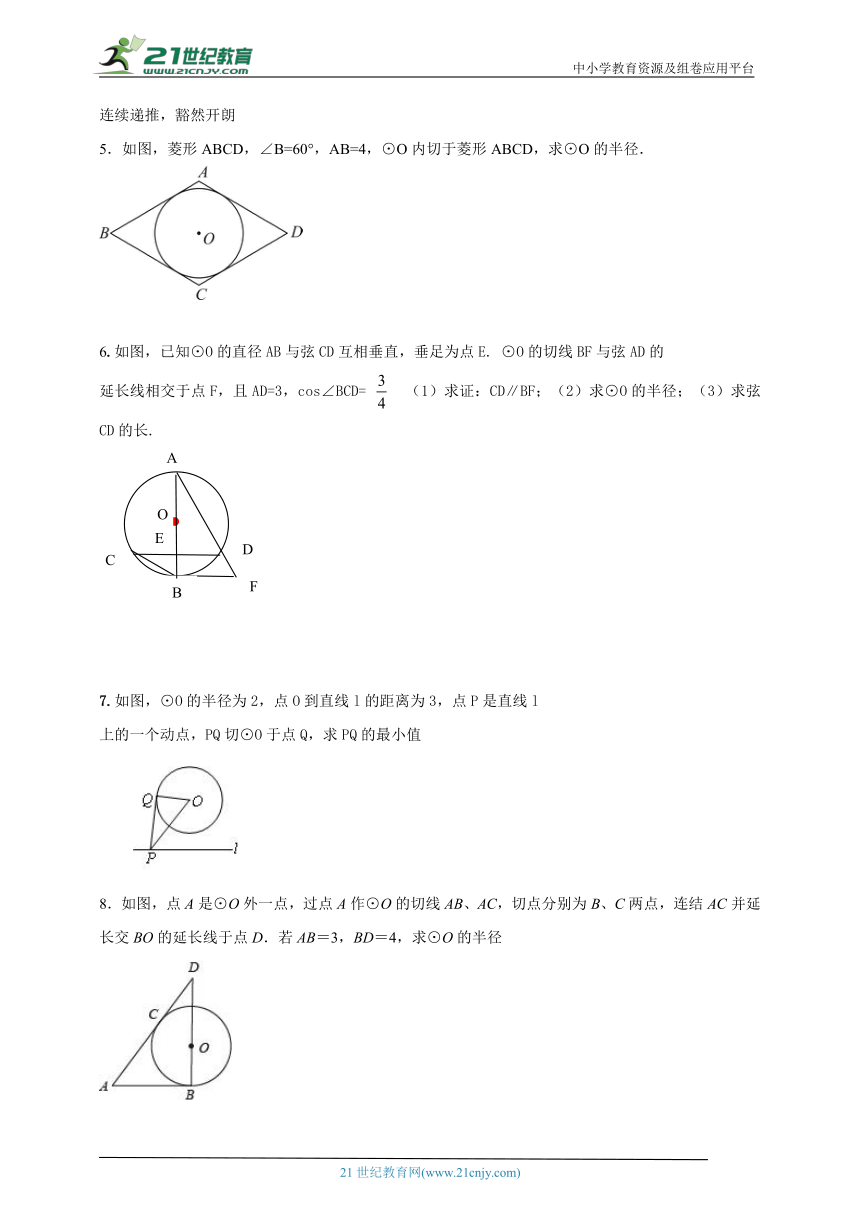
5.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,求⊙O的半径.
6.如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与弦AD的
延长线相交于点F,且AD=3,cos∠BCD= (1)求证:CD∥BF;(2)求⊙O的半径;(3)求弦CD的长.
7.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l
上的一个动点,PQ切⊙O于点Q,求PQ的最小值
8.如图,点A是⊙O外一点,过点A作⊙O的切线AB、AC,切点分别为B、C两点,连结AC并延长交BO的延长线于点D.若AB=3,BD=4,求⊙O的半径
思维拓展,更上一层
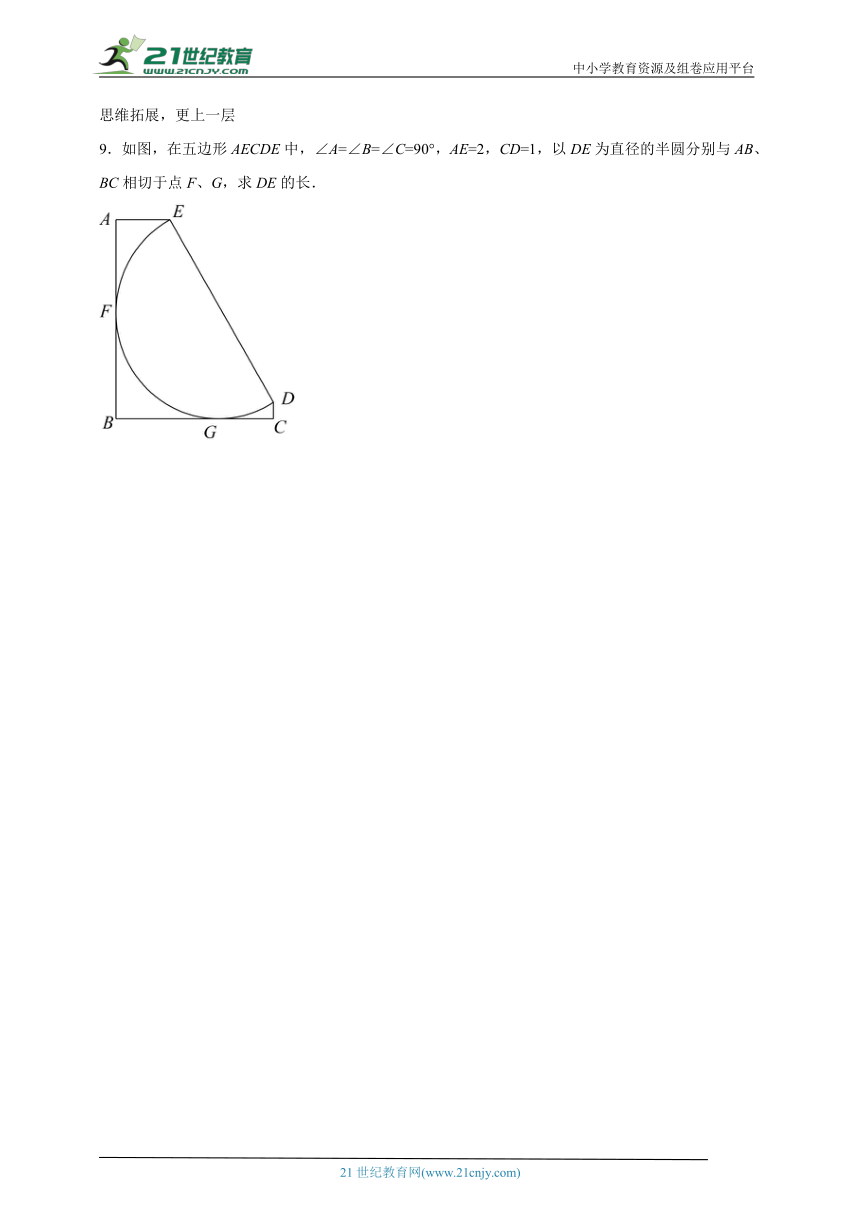
9.如图,在五边形AECDE中,∠A=∠B=∠C=90°,AE=2,CD=1,以DE为直径的半圆分别与AB、BC相切于点F、G,求DE的长.
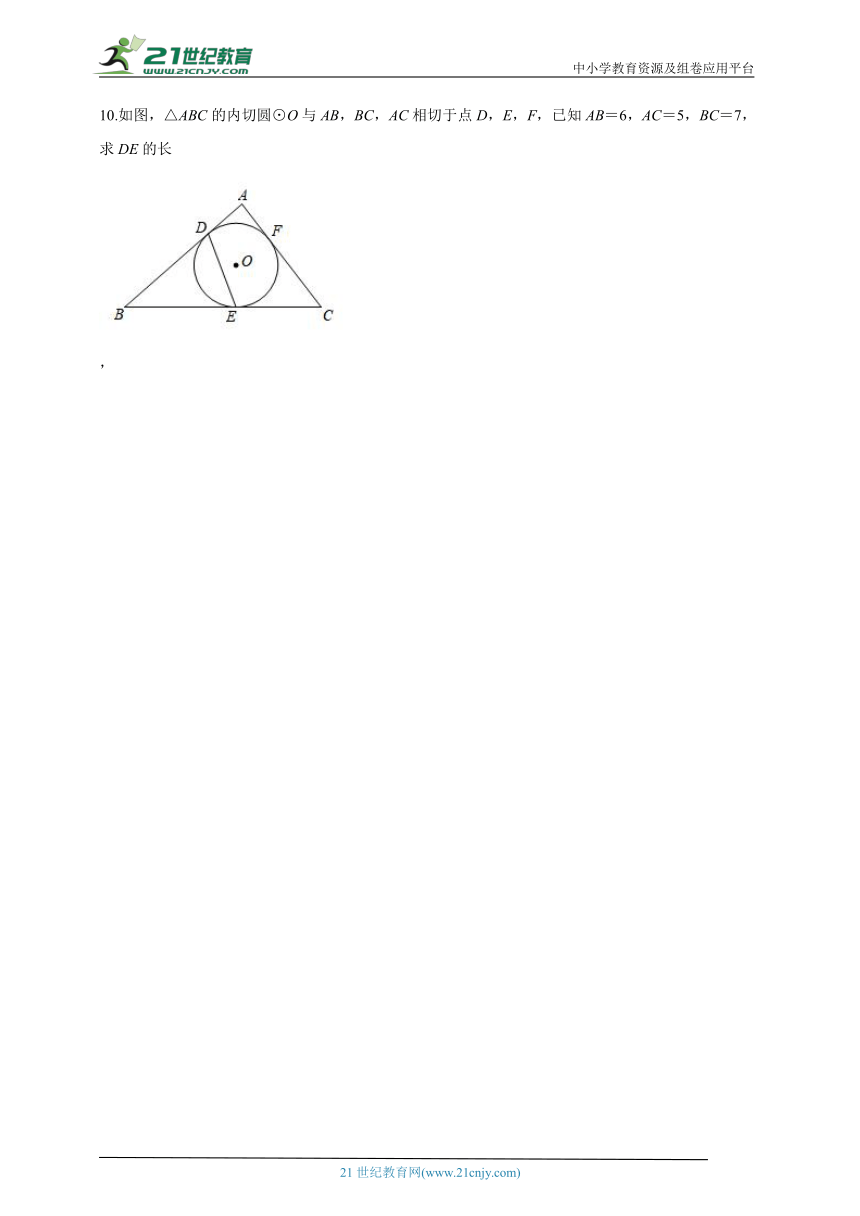
10.如图,△ABC的内切圆⊙O与AB,BC,AC相切于点D,E,F,已知AB=6,AC=5,BC=7,求DE的长
,
和切线有关的计算专项训练(2)
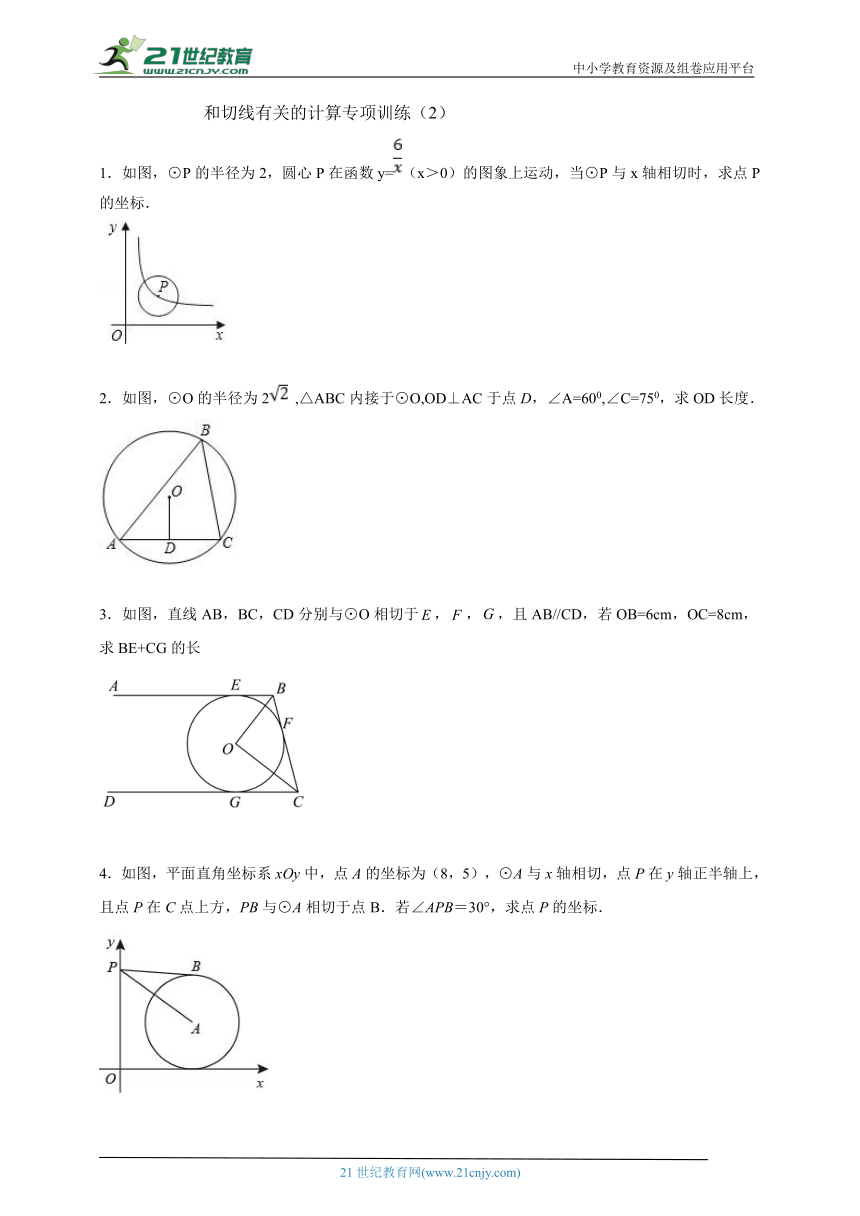
1.如图,⊙P的半径为2,圆心P在函数y=(x>0)的图象上运动,当⊙P与x轴相切时,求点P的坐标.
2.如图,⊙O的半径为2 ,△ABC内接于⊙O,OD⊥AC于点D,∠A=600,∠C=750,求OD长度.
3.如图,直线AB,BC,CD分别与⊙O相切于,,,且AB//CD,若OB=6cm,OC=8cm,求BE+CG的长
4.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,且点P在C点上方,PB与⊙A相切于点B.若∠APB=30°,求点P的坐标.
连续递推,豁然开朗
5.木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设角尺的较长边足够长,角尺的顶点为B,较短边AB=8cm,若读得BC长为acm,用含a的代数式表示r.
6.如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,求 的值.
7.如图,菱形ABCD的边长为10,面积为80,∠BAD<90°,⊙O与边AB,AD都相切,菱形的顶点A到圆心O的距离为5,求⊙O的半径长
8.如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC= ,求⊙O的半径
思维拓展,更上一层
1.如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,过点O,E的直线交CF于点G,求CF的长
2.如图,AB为的直径,延长AB到点P,过点P作的切线PC,PD,切点分别为C,D,连接CD交AP于点M,连接BD,AD.若PC=2,tan∠BDC=,求AD的长
和切线有关的计算专项训练(1)参考答案
1.∵大圆的弦AB切小圆于点 C,∴OC⊥AB,∴AB=2AC,
∵OD=2,∴OC=2,∵tan∠OAB=,∴AC=4,∴AB=8,
2.四边形ABCD为平行四边形,BC与相切于点B
,AB=CD又
3.解:连接OD,∵DF为圆O的切线,∴OD⊥DF,∵△ABC为等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°,∵OD=OC,∴△OCD为等边三角形,∴OD∥AB,
又O为BC的中点,∴D为AC的中点,即OD为△ABC的中位线,∴OD∥AB,∴DF⊥AB,
在Rt△AFD中,∠ADF=30°,AF=2,∴AD=4,即AC=8,∴FB=AB-AF=8-2=6,
在Rt△BFG中,∠BFG=30°,则根据勾股定理得:FG=3.
4.【详解】设切点分别为G,E,连接PG,PE,PC,PD,并延长EP交BC与F,则PG=PE=PC=5,四边形OBFE是矩形.∵OA=8,∴CF=8-5=3,∴PF=4,∴OB=EF=5+4=9.
∵PF过圆心,∴DF=CF=3,∴BD=8-3-3=2,∴D(9,2).
5.【详解】设AB和BC上的切点分别为E、F,连接OA、OE、OB、OF,则,
内切于菱形ABCD,平分
同理得
6.解:(1)∵BF是⊙O的切线 ∴AB⊥BF 。 ∵AB⊥CD , ∴CD∥BF 。
(2)连结BD ∵AB是直径,∴∠ADB=90°。 ∵∠BCD=∠BAD,cos∠BCD=。
∴cos∠BAD=。 又∵AD=3, ∴AB=4。∴⊙O的半径为2 。
(3)∵cos∠DAE= ,AD=3,∴AE= 。
∴ED= 。 ∴CD=2ED= 。
7.因为PQ为切线,所以△OPQ是Rt△.又OQ为定值,所以当OP最小时,PQ最小.根据垂线段最短,知OP=3时PQ最小.运用勾股定理得PQ=。
8.解:连接,点A是⊙O外一点,过点A作⊙O的切线AB、AC,切点分别为B、C两点,
,,∴,
在中,∠ABD=900,AB=3,BD=4,由勾股定理得,
,设半径,则,
在中,,CD=2,,,
由勾股定理知,得,即,解得,
9.【详解】解:取DE的中点O,连接OF、OG,延长GO与AE的延长线相交于点M,过点D作DN⊥MG于点N,
∵BC切⊙O于点G,∴CG⊥BG,∵∠A=∠B=∠C=90°,
∴四边形ABGM、四边形GCDN和四边形OFBG都是矩形,
∵OF=OG,∴四边形OFBG是正方形,
设⊙O的半径为r,则OE=OD=OE=OG=BG=AM= r,
∵AE=2,CD=1,∴ME=r -2,ON=r-1,
在Rt△OME和Rt△OND中,,
∴Rt△OME≌Rt△OND,∴OM= ON=r-1,
在Rt△OME中,OE2=ME2+OM2,∴r2=( r -2)2+( r-1)2,解得:r=1(舍去)或5,
10【详解】解:连接、、,交于,作交BC于点G,如图,
∵AB=6,AC=5,BC=7,
∴,即,解得:,
∴,∴,
设内切圆的半径为r,则,解得:,
的内切圆⊙与,,分别相切于点,,,
∴∠ODB=∠OEB=90°,又∵OD=OE, OB=OB, ∴,
∴BD=BE,同理, CE=CF,AD=AF,∵BE+CE=BC=7, ∴BD+BE+CE+CF=14,
∴2AD=(6+5+7)-14=4,即AD=2,∴,∴,
,,垂直平分,,,
,,,
和切线有关的计算专项训练(2)参考答案
1: 解:根据题意可知,把y=2代入得:x=3,∴点P的坐标是(3,2).
2..解:如图所示,连接OA、OC,
由题意得:,∴∠AOC=90°,
∵的半径为,OA=OC,∴OA=OC=,∠OAD=45°,
∵, ∴sin∠OAD=,解得:OD=2.
3.【详解】解: ,,
、,分别与相切于、、,
,,,,
,,,.
4.【详解】如下图所示,连接AB,作AD⊥x轴,AC⊥y轴,
∵PB与⊙A相切于点B∴AB⊥PB,∵∠APB=30°,AB⊥PB,∴PA=2AB=.
∵∴四边形ACOD是矩形,
点A的坐标为(8,5),所以AC=OD=8,CO=AD=5,
在中,.
∴,∴点P的坐标为.
5. 解:①如图所示,0<r≤8时,∵OA⊥BA,OC⊥BC,∠B=90°,∴四边形OABC是矩形,∴BC=AO,∴r=a;②当r>8时,如图:连接OC,∵BC与⊙O相切于点C,∴OC⊥BC,连接OA,过点A作AD⊥OC于点D,则四边形ABCD是矩形,即AD=BC,CD=AB.在Rt△AOD中,OA2=OD2+AD2,即:r2=(r﹣8)2+a2,整理得:r=a2+4.
6.【解答】解:设AM=x,BM=y,
∵圆O内切于五边形ABCDE,
∴AM=AR,BM=BN,CN=CP,DP=DQ,EQ=ER,AR=AM,∴BN=y,
∵AB=5,∴x+y=5,∵BC=7,∴CN=CP=7﹣y,∵CD=8,∴DQ=DP=y+1,
∵DE=9,∴EQ=ER=8﹣y,∵EA=4,∴AR=AM=y﹣4,∴y﹣4=x,
∴ ,解得: ,∴AM= ,MB= ,∴ = = ;
7.【解析】如图,取F点,连接OF,连接BD,交AC于E点,
∵AD为切线,∴OF⊥AF,∵四边形ABCD为菱形,∴BD⊥AC,
∵S菱形ABCD= AC×BD=80,
又∵DE2+AE2=AD2,即AC2+BD2=400,
∴,
解得:AC= 或 (舍去),∴BD= ,∴ED= ,
∵∠AED=∠AFO=90°,∠OAF=∠EAD,∴△AOF∽△AED,
∴,即 ,
解得:OF= .
8.【解析】连接CO并延长交AB于D,连接OA,
∵MN是⊙O的切线,∴MN⊥CD,∵MN∥AB,∴CD⊥AB,∴AD= AB= ×2=1,
在Rt△ACD中,AC= ,由勾股定理得:CD= =2,
设⊙O的半径为r,则OD=2﹣r,OA=r,在Rt△AOD中,r2=12+(2﹣r)2,r= ,
则⊙O的半径为 ;
9.解:过点O作OH⊥B′C于点H,∴∠OHB′=90°,
∵A'B'与⊙O相切于点E,∴∠OEB′=90°,
∵四边形ABCD是矩形,∴AB=CD=5,∴OD=OC=OE=2.5,
由旋转得:BC=B′C=4,∵四边形A′B′C′D′是矩形,∴∠B′=∠B′CD′=90°,
四边形OEB′H和四边形EB′CG都是矩形,∴B′H=OE=2.5,B′E=OH=CG,∠EGC=90°,
∴CH=B′C﹣B′H=1.5,∴OH===2,
∴CG=OH=2,∵OG⊥CD′,∴CF=2CG=4,
10.【详解】解:连接,如图所示,
∵PC,PD是的切线,∴ 设∵∴
∴
设的半径为∴在中,,解得,
在中,∵是的切线, ∴
在中,∵
∵∴整理得,
∴解得,或(舍去)
∴∴
在中,
A
B
C
D
F
E
O
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
和切线有关的计算专项训练(1)
夯实基础,稳扎稳打
1.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA交小圆于点D,若OD=2,tan∠OAB=,求AB的长
2.如图,ABCD的边BC与相切于点B,AD为的直径,若,求CD的长
3.如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,求FG的长
4.如图,在平面直角坐标系中,点在第一象限,⊙P与x轴、y轴都相切,且经过矩形的顶点C,与BC相交于点D,若⊙P的半径为5,点的坐标是,求点D的坐标
连续递推,豁然开朗
5.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,求⊙O的半径.
6.如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与弦AD的
延长线相交于点F,且AD=3,cos∠BCD= (1)求证:CD∥BF;(2)求⊙O的半径;(3)求弦CD的长.
7.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l
上的一个动点,PQ切⊙O于点Q,求PQ的最小值
8.如图,点A是⊙O外一点,过点A作⊙O的切线AB、AC,切点分别为B、C两点,连结AC并延长交BO的延长线于点D.若AB=3,BD=4,求⊙O的半径
思维拓展,更上一层
9.如图,在五边形AECDE中,∠A=∠B=∠C=90°,AE=2,CD=1,以DE为直径的半圆分别与AB、BC相切于点F、G,求DE的长.
10.如图,△ABC的内切圆⊙O与AB,BC,AC相切于点D,E,F,已知AB=6,AC=5,BC=7,求DE的长
,
和切线有关的计算专项训练(2)
1.如图,⊙P的半径为2,圆心P在函数y=(x>0)的图象上运动,当⊙P与x轴相切时,求点P的坐标.
2.如图,⊙O的半径为2 ,△ABC内接于⊙O,OD⊥AC于点D,∠A=600,∠C=750,求OD长度.
3.如图,直线AB,BC,CD分别与⊙O相切于,,,且AB//CD,若OB=6cm,OC=8cm,求BE+CG的长
4.如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,且点P在C点上方,PB与⊙A相切于点B.若∠APB=30°,求点P的坐标.
连续递推,豁然开朗
5.木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设角尺的较长边足够长,角尺的顶点为B,较短边AB=8cm,若读得BC长为acm,用含a的代数式表示r.
6.如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,求 的值.
7.如图,菱形ABCD的边长为10,面积为80,∠BAD<90°,⊙O与边AB,AD都相切,菱形的顶点A到圆心O的距离为5,求⊙O的半径长
8.如图,已知A、B、C为⊙O上三点,过C的切线MN∥弦AB,AB=2,AC= ,求⊙O的半径
思维拓展,更上一层
1.如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'CD'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,过点O,E的直线交CF于点G,求CF的长
2.如图,AB为的直径,延长AB到点P,过点P作的切线PC,PD,切点分别为C,D,连接CD交AP于点M,连接BD,AD.若PC=2,tan∠BDC=,求AD的长
和切线有关的计算专项训练(1)参考答案
1.∵大圆的弦AB切小圆于点 C,∴OC⊥AB,∴AB=2AC,
∵OD=2,∴OC=2,∵tan∠OAB=,∴AC=4,∴AB=8,
2.四边形ABCD为平行四边形,BC与相切于点B
,AB=CD又
3.解:连接OD,∵DF为圆O的切线,∴OD⊥DF,∵△ABC为等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°,∵OD=OC,∴△OCD为等边三角形,∴OD∥AB,
又O为BC的中点,∴D为AC的中点,即OD为△ABC的中位线,∴OD∥AB,∴DF⊥AB,
在Rt△AFD中,∠ADF=30°,AF=2,∴AD=4,即AC=8,∴FB=AB-AF=8-2=6,
在Rt△BFG中,∠BFG=30°,则根据勾股定理得:FG=3.
4.【详解】设切点分别为G,E,连接PG,PE,PC,PD,并延长EP交BC与F,则PG=PE=PC=5,四边形OBFE是矩形.∵OA=8,∴CF=8-5=3,∴PF=4,∴OB=EF=5+4=9.
∵PF过圆心,∴DF=CF=3,∴BD=8-3-3=2,∴D(9,2).
5.【详解】设AB和BC上的切点分别为E、F,连接OA、OE、OB、OF,则,
内切于菱形ABCD,平分
同理得
6.解:(1)∵BF是⊙O的切线 ∴AB⊥BF 。 ∵AB⊥CD , ∴CD∥BF 。
(2)连结BD ∵AB是直径,∴∠ADB=90°。 ∵∠BCD=∠BAD,cos∠BCD=。
∴cos∠BAD=。 又∵AD=3, ∴AB=4。∴⊙O的半径为2 。
(3)∵cos∠DAE= ,AD=3,∴AE= 。
∴ED= 。 ∴CD=2ED= 。
7.因为PQ为切线,所以△OPQ是Rt△.又OQ为定值,所以当OP最小时,PQ最小.根据垂线段最短,知OP=3时PQ最小.运用勾股定理得PQ=。
8.解:连接,点A是⊙O外一点,过点A作⊙O的切线AB、AC,切点分别为B、C两点,
,,∴,
在中,∠ABD=900,AB=3,BD=4,由勾股定理得,
,设半径,则,
在中,,CD=2,,,
由勾股定理知,得,即,解得,
9.【详解】解:取DE的中点O,连接OF、OG,延长GO与AE的延长线相交于点M,过点D作DN⊥MG于点N,
∵BC切⊙O于点G,∴CG⊥BG,∵∠A=∠B=∠C=90°,
∴四边形ABGM、四边形GCDN和四边形OFBG都是矩形,
∵OF=OG,∴四边形OFBG是正方形,
设⊙O的半径为r,则OE=OD=OE=OG=BG=AM= r,
∵AE=2,CD=1,∴ME=r -2,ON=r-1,
在Rt△OME和Rt△OND中,,
∴Rt△OME≌Rt△OND,∴OM= ON=r-1,
在Rt△OME中,OE2=ME2+OM2,∴r2=( r -2)2+( r-1)2,解得:r=1(舍去)或5,
10【详解】解:连接、、,交于,作交BC于点G,如图,
∵AB=6,AC=5,BC=7,
∴,即,解得:,
∴,∴,
设内切圆的半径为r,则,解得:,
的内切圆⊙与,,分别相切于点,,,
∴∠ODB=∠OEB=90°,又∵OD=OE, OB=OB, ∴,
∴BD=BE,同理, CE=CF,AD=AF,∵BE+CE=BC=7, ∴BD+BE+CE+CF=14,
∴2AD=(6+5+7)-14=4,即AD=2,∴,∴,
,,垂直平分,,,
,,,
和切线有关的计算专项训练(2)参考答案
1: 解:根据题意可知,把y=2代入得:x=3,∴点P的坐标是(3,2).
2..解:如图所示,连接OA、OC,
由题意得:,∴∠AOC=90°,
∵的半径为,OA=OC,∴OA=OC=,∠OAD=45°,
∵, ∴sin∠OAD=,解得:OD=2.
3.【详解】解: ,,
、,分别与相切于、、,
,,,,
,,,.
4.【详解】如下图所示,连接AB,作AD⊥x轴,AC⊥y轴,
∵PB与⊙A相切于点B∴AB⊥PB,∵∠APB=30°,AB⊥PB,∴PA=2AB=.
∵∴四边形ACOD是矩形,
点A的坐标为(8,5),所以AC=OD=8,CO=AD=5,
在中,.
∴,∴点P的坐标为.
5. 解:①如图所示,0<r≤8时,∵OA⊥BA,OC⊥BC,∠B=90°,∴四边形OABC是矩形,∴BC=AO,∴r=a;②当r>8时,如图:连接OC,∵BC与⊙O相切于点C,∴OC⊥BC,连接OA,过点A作AD⊥OC于点D,则四边形ABCD是矩形,即AD=BC,CD=AB.在Rt△AOD中,OA2=OD2+AD2,即:r2=(r﹣8)2+a2,整理得:r=a2+4.
6.【解答】解:设AM=x,BM=y,
∵圆O内切于五边形ABCDE,
∴AM=AR,BM=BN,CN=CP,DP=DQ,EQ=ER,AR=AM,∴BN=y,
∵AB=5,∴x+y=5,∵BC=7,∴CN=CP=7﹣y,∵CD=8,∴DQ=DP=y+1,
∵DE=9,∴EQ=ER=8﹣y,∵EA=4,∴AR=AM=y﹣4,∴y﹣4=x,
∴ ,解得: ,∴AM= ,MB= ,∴ = = ;
7.【解析】如图,取F点,连接OF,连接BD,交AC于E点,
∵AD为切线,∴OF⊥AF,∵四边形ABCD为菱形,∴BD⊥AC,
∵S菱形ABCD= AC×BD=80,
又∵DE2+AE2=AD2,即AC2+BD2=400,
∴,
解得:AC= 或 (舍去),∴BD= ,∴ED= ,
∵∠AED=∠AFO=90°,∠OAF=∠EAD,∴△AOF∽△AED,
∴,即 ,
解得:OF= .
8.【解析】连接CO并延长交AB于D,连接OA,
∵MN是⊙O的切线,∴MN⊥CD,∵MN∥AB,∴CD⊥AB,∴AD= AB= ×2=1,
在Rt△ACD中,AC= ,由勾股定理得:CD= =2,
设⊙O的半径为r,则OD=2﹣r,OA=r,在Rt△AOD中,r2=12+(2﹣r)2,r= ,
则⊙O的半径为 ;
9.解:过点O作OH⊥B′C于点H,∴∠OHB′=90°,
∵A'B'与⊙O相切于点E,∴∠OEB′=90°,
∵四边形ABCD是矩形,∴AB=CD=5,∴OD=OC=OE=2.5,
由旋转得:BC=B′C=4,∵四边形A′B′C′D′是矩形,∴∠B′=∠B′CD′=90°,
四边形OEB′H和四边形EB′CG都是矩形,∴B′H=OE=2.5,B′E=OH=CG,∠EGC=90°,
∴CH=B′C﹣B′H=1.5,∴OH===2,
∴CG=OH=2,∵OG⊥CD′,∴CF=2CG=4,
10.【详解】解:连接,如图所示,
∵PC,PD是的切线,∴ 设∵∴
∴
设的半径为∴在中,,解得,
在中,∵是的切线, ∴
在中,∵
∵∴整理得,
∴解得,或(舍去)
∴∴
在中,
A
B
C
D
F
E
O
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
