第五章 平行四边形复习课(浙江省温州市苍南县)
文档属性
| 名称 | 第五章 平行四边形复习课(浙江省温州市苍南县) |  | |
| 格式 | rar | ||
| 文件大小 | 316.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-08 14:23:00 | ||
图片预览




文档简介
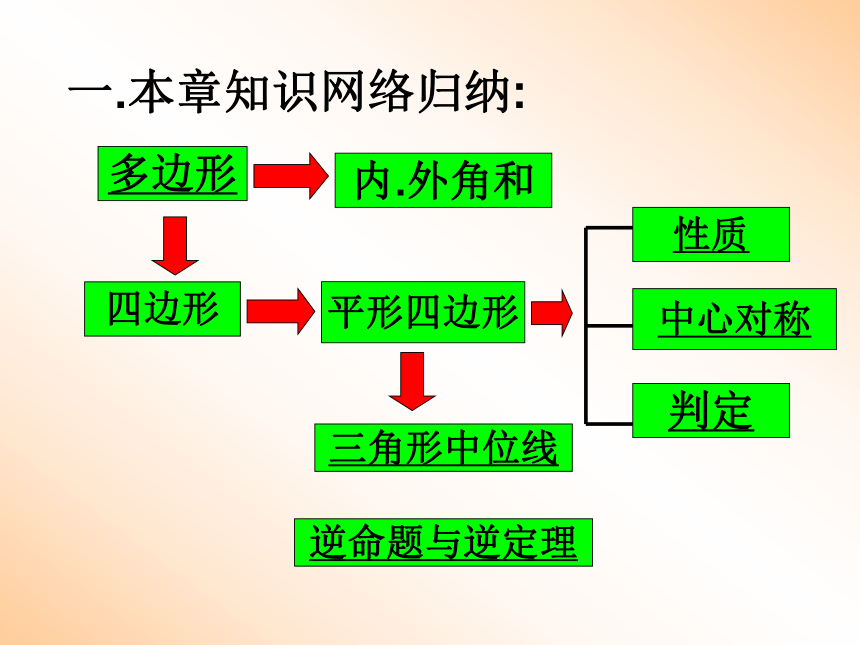
课件17张PPT。平行四边形复习课一.本章知识网络归纳:多边形内.外角和四边形平形四边形三角形中位线逆命题与逆定理n边形共有对角线 条(n≥3)2.多边形的对角线. n边形从一个顶点出发的对角线有(n-3)条(n≥3).n边形的内角和为:(n-2)×180°(n≥3).1.多边形的角n边形的外角和为:360°3.正边形能单独镶嵌的正多边形只有:正三角形,正方形,正六边形多边形典型例题2、四边形ABCD中,AD//BC,那么∠A:∠B:∠C:∠D的值可能是( ) 1、在一个四边形中,∠A:∠B:∠C:∠D=9:5:3:7,求这个四边形各内角的度数?A、9:5:3:7 B、2:3:4:5 C、3:5:2:4 D、2:5:4:33 、一个多边形,除了一个内角外,其余内角和为1205度,则这个内角是多少度,这是个几边形?平行四边形两组对边分别平行的四边形是平行四边形。1、平行四边形对边平行且相等
2、平行四边形对角相等 邻角互补
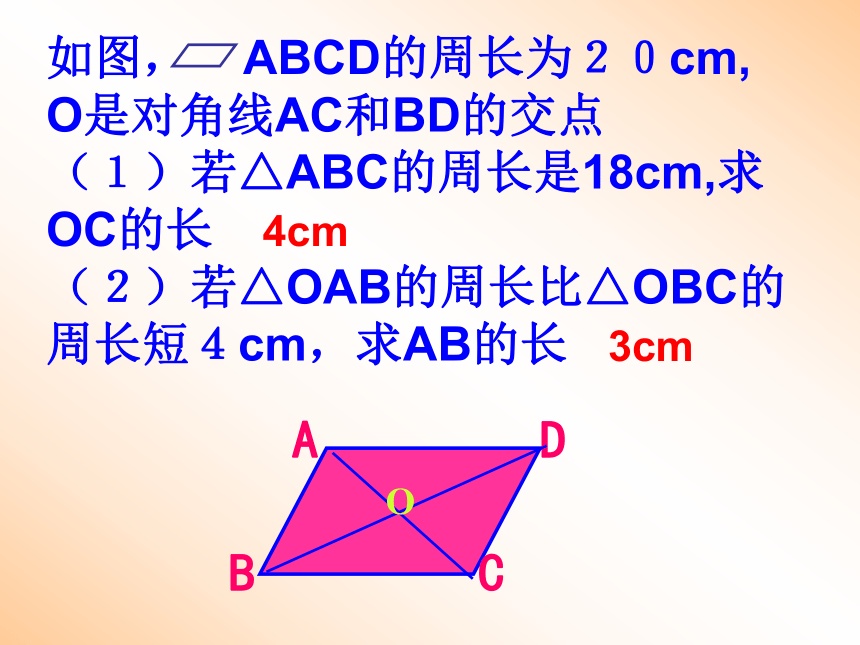
3、平行四边形对角线互相平分4、平行四边形是中心对称图形☆两个推论:夹在两条平行线间的平行线段相等夹在两条平行线间的垂线段相等☆性质:☆定义:如图, ABCD的周长为20cm, O是对角线AC和BD的交点
(1)若△ABC的周长是18cm,求OC的长
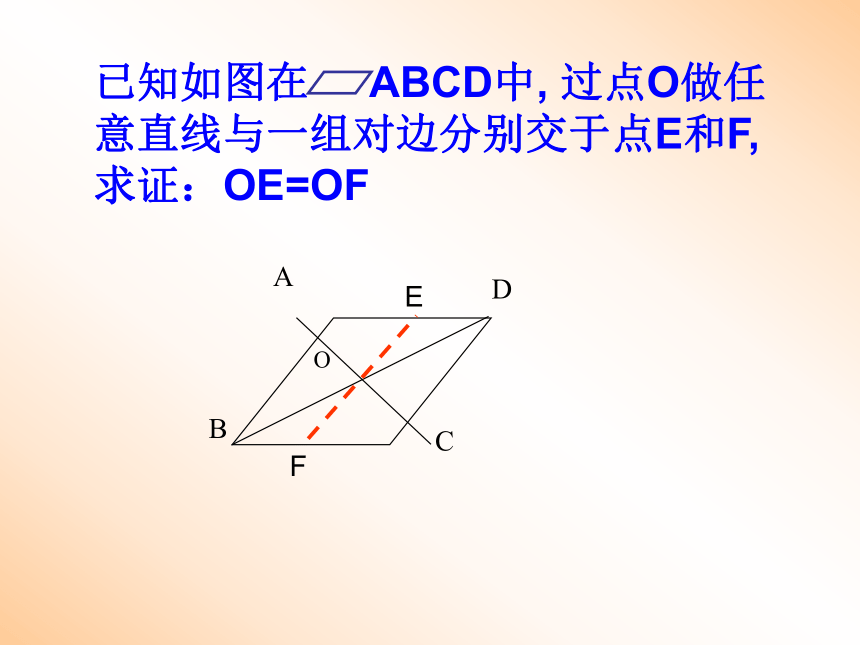
(2)若△OAB的周长比△OBC的周长短4cm,求AB的长4cm3cmEF已知如图在 ABCD中, 过点O做任意直线与一组对边分别交于点E和F,求证:OE=OF平行四边形的判定方法边:角:对角线:1.两组对边分别平行的四边形是平行四边形2.两组对边分别相等的四边形是平行四边形3.一组对边平行且相等的四边形是平行四边形5.两组对角分别相等的四边形是平行四边形4.对角线互相平分的四边形是平行四边形(注:第5条不能直接应用)判断题:
1.邻角互补的四边形是平行四边形.
2.一组对边平行,另一组对边相等的四边形是平行四边形.
3.一组对边平行, 一组对角相等的四边形是平行四边形.
4.对角线相等的四边形是平行四边形.如图在 ABCD中, E、F是对角线AC上的两点,且AE=CF, 求证:四边形BEDF是平行四边形O变式:已知如图四边形 ABCD和四边形BFDE都是平行四边形,
求证:AE=CF中心对称一个图形绕一点旋转180度后与原来图形重合.中心对称图形:关于一点成 中心对称:一个图形绕一点旋转180度后与另一图形互相重合.性质:对称中心平分连接两个对称点的线段直角坐标系中, 点(x,y)关于原点对称的点是(-x,-y)三角形中位线三角形的中位线平行于第三边,并且等于第三边的一半中位线定理:几个倍半关系平行四边形邻边长的和等于半周长
中点三角形的周长等于大三角形的一半
直角三角形中斜边的中线等于斜边的一半逆命题与逆定理重要逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.如果三角形一边上的中线等于这边一半,那么这个三角形是直角三角形定理3:定理2:定理1:已知:如图,在?ABCD中,E,F分别是AD,BC的中点.
求证:MN∥BC,且MN=BC已知:如图,四边形ABCD是平行四边形,△ADE和△BCF都是等边三角形.求证:BD和EF互相平分.ABCFDE已知:如图,O是等边三角形ABC内任意一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,AC上.
求证:OD+OE+OF=BC.AFOEDBCMN谢谢合作!
2、平行四边形对角相等 邻角互补
3、平行四边形对角线互相平分4、平行四边形是中心对称图形☆两个推论:夹在两条平行线间的平行线段相等夹在两条平行线间的垂线段相等☆性质:☆定义:如图, ABCD的周长为20cm, O是对角线AC和BD的交点
(1)若△ABC的周长是18cm,求OC的长
(2)若△OAB的周长比△OBC的周长短4cm,求AB的长4cm3cmEF已知如图在 ABCD中, 过点O做任意直线与一组对边分别交于点E和F,求证:OE=OF平行四边形的判定方法边:角:对角线:1.两组对边分别平行的四边形是平行四边形2.两组对边分别相等的四边形是平行四边形3.一组对边平行且相等的四边形是平行四边形5.两组对角分别相等的四边形是平行四边形4.对角线互相平分的四边形是平行四边形(注:第5条不能直接应用)判断题:
1.邻角互补的四边形是平行四边形.
2.一组对边平行,另一组对边相等的四边形是平行四边形.
3.一组对边平行, 一组对角相等的四边形是平行四边形.
4.对角线相等的四边形是平行四边形.如图在 ABCD中, E、F是对角线AC上的两点,且AE=CF, 求证:四边形BEDF是平行四边形O变式:已知如图四边形 ABCD和四边形BFDE都是平行四边形,
求证:AE=CF中心对称一个图形绕一点旋转180度后与原来图形重合.中心对称图形:关于一点成 中心对称:一个图形绕一点旋转180度后与另一图形互相重合.性质:对称中心平分连接两个对称点的线段直角坐标系中, 点(x,y)关于原点对称的点是(-x,-y)三角形中位线三角形的中位线平行于第三边,并且等于第三边的一半中位线定理:几个倍半关系平行四边形邻边长的和等于半周长
中点三角形的周长等于大三角形的一半
直角三角形中斜边的中线等于斜边的一半逆命题与逆定理重要逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.如果三角形一边上的中线等于这边一半,那么这个三角形是直角三角形定理3:定理2:定理1:已知:如图,在?ABCD中,E,F分别是AD,BC的中点.
求证:MN∥BC,且MN=BC已知:如图,四边形ABCD是平行四边形,△ADE和△BCF都是等边三角形.求证:BD和EF互相平分.ABCFDE已知:如图,O是等边三角形ABC内任意一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,AC上.
求证:OD+OE+OF=BC.AFOEDBCMN谢谢合作!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
