2023—2024学年浙教版八年级数学上册第2章特殊三角形单元达标测试卷(含解析)
文档属性
| 名称 | 2023—2024学年浙教版八年级数学上册第2章特殊三角形单元达标测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 422.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-30 19:04:37 | ||
图片预览



文档简介
浙教版八年级数学上册第2章特殊三角形单元达标测试卷
一、单选题
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.如图,若 与 关于直线 对称, 交 于点 ,则下列说法中,不一定正确的是( )
A. B.
C. D.
3.下列四个图标中,属于轴对称图形的是( )
A. B. C. D.
4.在下列条件中,能确定 是直角三角形的条件有( )
A. B.
C. D.
5.柯桥区作为浙江省试点先行区,四年前就开始实行垃圾分类,以下是几种垃圾分类的图标,其中哪个几何图标是轴对称图形( )
A. B. C. D.
6.对于题目:如图, 是 的角平分线, 于点 ,若 ,求 的度数.下面是打乱了的解题过程:①∵ ;② ;③∵ 平分 ,∴ ;④∵ , ,则下列排序正确的是( ).
A.③④②① B.④②①③ C.③②④① D.③①④②
7.如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
8.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三个角的度数比为1:2:3 B.三条边的长度比为1:2:3
C.三条边满足关系a2+c2=b2 D.三个角满足关系∠B+∠C=∠A
9.下列各组数不是勾股数的是( )
A.2、3、4 B.3、4、5 C.6、8、10 D.5、12、13
10.如图,在△ABC中,AB=AC,AD,BE是△ABC的两条中线,P是AD上的一个动点,则下列线段的长等于CP+EP最小值的是( )
A.AC B.AD C.BE D.BC
二、填空题
11.如果一个直角二角形的两条直角边的长分别是5和12,那么这个直角三角形斜边长是 。
12.如图,A、B、C三点在同一条直线上,∠A=50°,BD垂直平分AE,垂足为D,则∠EBC的度数为 .
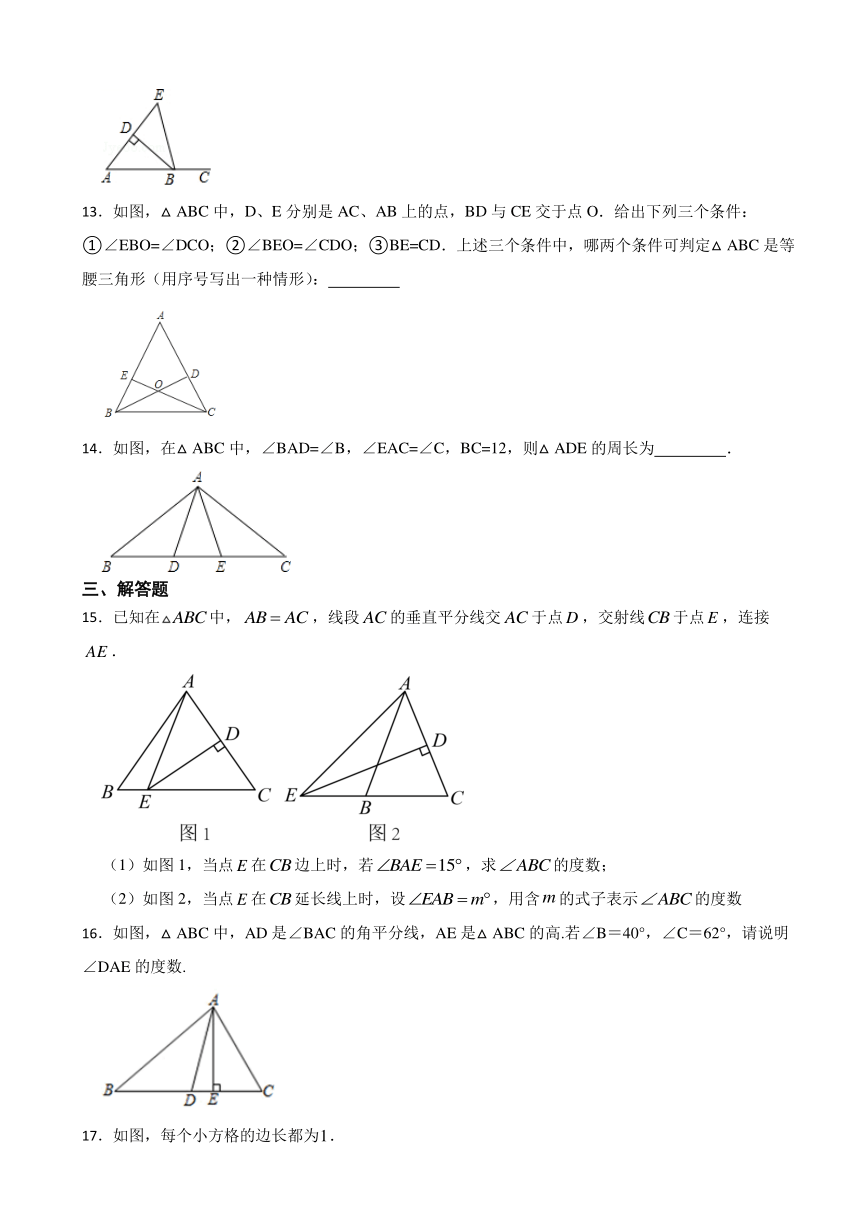
13.如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):
14.如图,在△ABC中,∠BAD=∠B,∠EAC=∠C,BC=12,则△ADE的周长为 .
三、解答题
15.已知在中,,线段的垂直平分线交于点,交射线于点,连接.
(1)如图1,当点在边上时,若,求的度数;
(2)如图2,当点在延长线上时,设,用含的式子表示的度数
16.如图,△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.若∠B=40°,∠C=62°,请说明∠DAE的度数.
17.如图,每个小方格的边长都为.
(1)求图中格点四边形的面积;
(2)请探究:与的位置关系,并说明理由.
18.如图,在△ABC中,AB=AC,AD为BC边上的中线,∠CAD=40°,EF为过点A的一条直线,且EF∥BC,求∠BAE的度数.
四、综合题
19.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,EB平分∠DEC.
(1)求证:BC=CE;
(2)若CE=AB,EA=EB,求∠C的度数.
20.如图,在平面直角坐标系中完成下列各题:(不写作法,保留作图痕迹)
(1)在图一中作出△ABC关于y轴对称的△A1B1C1并写出A1、B1、C1的坐标.
(2)在图二中x轴上画出点P,使PA+PB的值最小.
21.已知a、b、c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数,①求c的长;
②判断△ABC的形状.
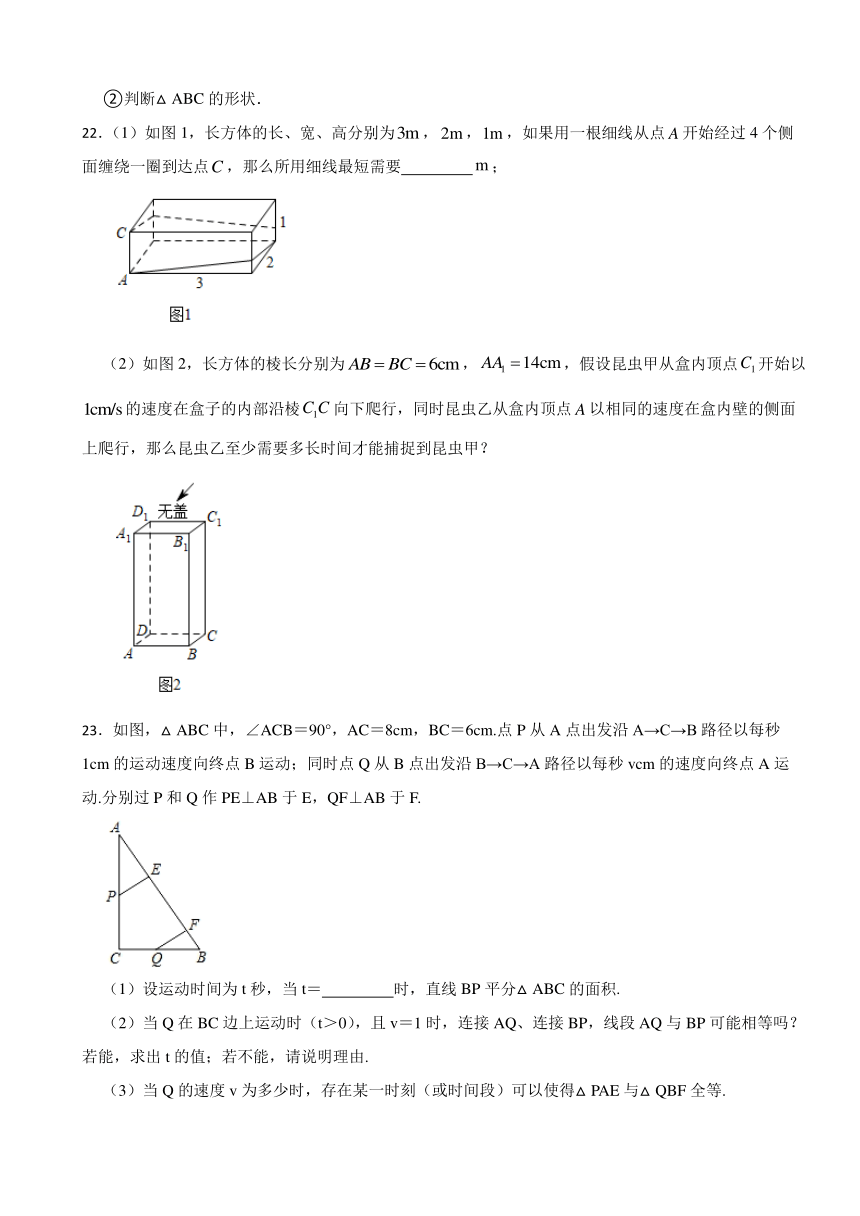
22.(1)如图1,长方体的长、宽、高分别为,,,如果用一根细线从点开始经过4个侧面缠绕一圈到达点,那么所用细线最短需要 ;
(2)如图2,长方体的棱长分别为,,假设昆虫甲从盒内顶点开始以的速度在盒子的内部沿棱向下爬行,同时昆虫乙从盒内顶点以相同的速度在盒内壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
23.如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动;同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动.分别过P和Q作PE⊥AB于E,QF⊥AB于F.
(1)设运动时间为t秒,当t= 时,直线BP平分△ABC的面积.
(2)当Q在BC边上运动时(t>0),且v=1时,连接AQ、连接BP,线段AQ与BP可能相等吗?若能,求出t的值;若不能,请说明理由.
(3)当Q的速度v为多少时,存在某一时刻(或时间段)可以使得△PAE与△QBF全等.
答案解析部分
1.【答案】C
【解析】【解答】解:A、是轴对称图形,不符合题意;
B、是轴对称图形,不符合题意;
C 、是中心对称图形,不是轴对称图形,符合题意;
D、是轴对称图形,不符合题意.
故答案为:C.
【分析】 本题考查轴对称图形的概念. 轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
2.【答案】B
【解析】【解答】解:∵ 与 关于直线 对称,
∴ , , ,
故答案为:B.
【分析】根据轴对称的性质逐一判断即可.
3.【答案】B
【解析】【解答】解:A、不是轴对称图形,故此选项不符合题意;
B、是轴对称图形,故此选项符合题意;
C、不是轴对称图形,故此选项不符合题意;
D、不是轴对称图形,故此选项不符合题意.
故答案为:B.
【分析】将一个平面图形沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,根据轴对称图形的概念一一判断即可.
4.【答案】B
【解析】【解答】解:A、 ,
是等边三角形,故 选项不符合题意;
B、 ,
是直角三角形,故 选项 符合题意;
C、 ,
为最大角,
不是直角三角形;故 选项不符合题意;
D、 ,
所以不能判定 是直角三角形,
故 不符合题意,
故答案为:B.
【分析】确定三角形是直角三角形的条件是有一个角是直角,然后根据三角形的内角和定理分别进行解答并判断即可.
5.【答案】B
【解析】【解答】解:A、不是轴对称图形,故此选项错误;
B、是轴对称图形,故此选项正确;
C、不是轴对称图形,故此选项错误;
D、不是轴对称图形,故此选项错误.
故答案为:B.
【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,根据轴对称图形的定义,依次对各选项进行判断即可.
6.【答案】A
【解析】【解答】∵ 平分
∴
∵
∴
∴
∴
故答案为:A.
【分析】根据角平分线的性质,可得,利用垂直的定义得出,根据直角三角形两锐角互余得出 ,从而求出,据此判断即可.
7.【答案】A
【解析】【解答】解:∵AB的垂直平分线DE交AC于D,交AB于E,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠CBD=∠ABD=36°,
即BD平分∠ABC;故①正确;
∴∠BDC=∠C=72°,
∴BC=BD,
∴BC=BD=AD,故②正确;
∴△BDC的周长为:BC+CD+BD=BC+CD+AD=AC+BC=AB+BC;故③正确;
∵CD<BD,
∴CD<AD,
∴D不是AC中点.故④错误.
故答案为:A.
【分析】由AB的垂直平分线DE交AC于D,交AB于E,可得AD=BD,即可求得∠ABD=∠A=36°,又由AB=AC,即可求得∠CBD=∠ABD=36°,∠BDC=∠C=72°,继而证得AD=BD=BC,△BDC的周长等于AB+BC.
8.【答案】B
【解析】【解答】解:A、三个角的度数比为1:2:3,最大角的度数是90°,是直角三角形,不符合题意;
B、三条边的比为1:2:3,12+22≠32,不是直角三角形,符合题意;
C、三条边满足关系a2+c2=b2,是直角三角形,不符合题意;
D、三个角满足关系∠B+∠C=∠A,所以∠A=90°,是直角三角形,不符合题意;
故答案为:B.
【分析】根据勾股定理的逆定理以及直角三角形的定义判断即可。
9.【答案】A
【解析】【解答】 解:A. 22+32≠42,故A选项不是勾股数;
B. 32+42=52,故B选项是勾股数;
C. 62+82=102 ,故C选项是勾股数;
D. 52+122=132,故D选项是勾股数;故选A.
10.【答案】C
【解析】【解答】解:如图,连接PB,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴PB=PC,
∴PC+PE=PB+PE,
∵PE+PB≥BE,
∴P、B、E共线时,PB+PE的值最小,最小值为BE的长度,
故答案为:C.
【分析】如图连接PB,只要证明PB=PC,即可推出PC+PE=PB+PE,由PE+PB≥BE,可得P、B、E共线时,PB+PE的值最小,最小值为BE的长度.
11.【答案】13
【解析】【解答】
因为5 +12 =13
所以斜边等于13
【分析】考查勾股定理的性质;难题较低且属于常考题型。在直角三角形中,两直角边的平方和等于斜边的平方。注意求解出来的结果取的是正根
12.【答案】100°
【解析】【解答】∵BD垂直平分AE,
∴
∴
∴
故答案为100°.
【分析】根据线段垂直平分线的性质,得 根据等腰三角形的性质,得 再根据三角形外角的性质即可求解.
13.【答案】①③
【解析】【解答】答:由①③条件可判定△ABC是等腰三角形.
证明:∵∠EBO=∠DCO,∠EOB=∠DOC,(对顶角相等)
BE=CD,
∴△EBO≌△DCO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
【分析】根据已知条件求证△EBO≌△DCO,然后可得∠OBC=∠OCB再利用两角相等即可判定△ABC是等腰三角形.此题答案不唯一.
14.【答案】12
【解析】【解答】解:∵∠BAD=∠B,∠EAC=∠C,
∴AD=BD,AE=EC,
∴△ADE的周长=AD+DE+AE=BD+DE+EC=BC=12.
故答案是:12.
【分析】根据∠BAD=∠B,∠EAC=∠C,可得AD=BD,AE=EC,则△ADE的周长等于BC的长.
15.【答案】(1)解:垂直平分,
,
,
,
,
设,
在中,,
解得:,
;
(2)解:垂直平分,
,
,
,
,
设,
则,
在中,,
解得:,
∴.
【解析】【分析】(1)垂直平分线的性质的运用是解决本题的关键,利用其性质求得的等腰三角形AEC,进而得出底角相等∠C=∠EAC,利用等腰三角形的性质和三角形内角和定理就可以求得角的度数;
(2)类比(1)的思路进行求解即可.
16.【答案】解:∵ , ,
∴ ,
∵ 是 的平分线,
∴ ,
∵ 是 边上的高,
∴ 是直角三角形,
∴ ,
∴ .
【解析】【分析】先根据三角形内角和定理求∠BAC的度数,则可根据角平分线的定义求∠DAC,然后根据直角三角形的性质求出∠EAC,最后根据角的和差关系求∠DAE即可.
17.【答案】(1)解:,,
四边形的面积;
(2)解:由勾股定理,得,,
由题意可知,
,
为直角三角形,
,
.
【解析】【分析】(1)利用三角形的面积公式结合图形计算求解即可;
(2)利用勾股定理求出AD和CD的值,再求出△ACD为直角三角形,最后求解即可。
18.【答案】解:∵AB=AC, AD为BC边上的中线,
∴∠B=∠C,∠BAD=∠CAD=40°(三线合一),
∴∠BAC=∠BAD+∠CAD=80°,
∴,
∵EF∥BC,
∴∠BAE=∠B=50°.
【解析】【分析】根据等腰三角形的性质求出∠B=∠C,∠BAD=∠CAD,则可求出∠BAC的度数,然后根据等腰三角形的性质和三角形内角和定理求出∠B的度数,再根据平行线的性质求∠BAE度数即可.
19.【答案】(1)证明:∵EB平分∠DEC,
∴∠DEB=∠BEC.
∵DE∥BC.
∴∠DEB=∠EBC,
∴∠BEC=∠EBC,
∴BC=CE
(2)解:∵BC=CE,CE=AB,
∴BC=AB,
∴∠C=∠A,
设∠C=∠A=x,
∵EA=EB,
∴∠A=∠ABE=x,
∴∠EBC=∠BEC=∠A+∠ABE=2x,
∴2x+2x+x=180°,
∴∠C=x=36°
【解析】【分析】(1)根据角平分线以及平行线的性质:两直线平行内错角相等,即可得到∠BEC=∠EBC,再根据等腰三角形的判定,即可证明BC=CE.
(2)根据等腰三角形的性质:等腰三角形的两个底角相等,即可得到∠C=∠A,设∠A=∠C=x,又根据题意以及等腰三角形的性质可得∠A=∠ABE=x,根据三角形的任一外角等于与它不相邻的两个内角之和,再根据三角形的内角和为180°,即可列出方程,解出答案即可.
20.【答案】(1)解:如图一所示;
,
由图可知,A1(﹣1,2),B1(﹣3,1),C1(2,﹣1)
(2)解:如图二所示.
【解析】【分析】(1)画出各点关于y轴的对称点,再顺次连接并写出各点坐标即可;(2)作点A关于x轴的对称点A′,连接A′B交x轴于点P,则点P即为所求点.
21.【答案】(1)解:2<c<10;12<x<20
(2)解:①因为周长为小于18的偶数,所以x=16或x=14.
当x为16时,c=6;当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
【解析】【解答】解:(1)因为a=4,b=6,所以2<c<10.故周长x的范围为12<x<20
【分析】(1)根据三角形三边关系求出c的取值范围即可;
(2)①根据偶数的定义以及x的取值范围求出答案即可;
②利用等腰三角形的判定方法求出答案即可。
22.【答案】(1)
(2)解:设昆虫甲从顶点沿棱向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行,爬行捕捉到昆虫甲需x秒钟,
如图,在中,
∵长方体的棱长分别为,,
∴cm,cm,cm,cm,
∴,
解得:.
答:昆虫乙至少需要秒钟才能捕捉到昆虫甲.
【解析】【解答】解:(1)如图,将长方体展开,连接,
∵长方体的长、宽、高分别为,,,
∴这根细线最短的长为:m;
故答案为:.
【分析】(1)将长方体展开,连接AC,然后根据勾股定理计算即可求出这根细线最短的长;
(2)设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行,爬行捕捉到昆虫甲需x秒钟,由题意可得AB=BC=6cm,AA1=14cm,AF=xcm,C1F=xcm,CF=(14-x)cm,AC=12cm,然后利用勾股定理求解即可.
23.【答案】(1)4
(2)解:假设可能相等.则有82+(6﹣t)2=62+(8﹣t)2,
解得t=0,不符合题意,
所以当Q在BC边上运动时(t>0),且v=1时、线段AQ与BP不可能相等.
(3)解:①当点Q在线段BC上时,
在Rt△AEP和Rt△BFQ中,
∵∠AEP=∠BFQ=90°,∠C=90°,
∴∠A+∠B=90°,∠B+∠BQF=90°,
∴∠A=∠BQF,
∴当PA=BQ时,△AEP≌△FQB,
∴当v=1cm/s时,0<t≤6时,△PAE与△QBF全等.
②当P,Q在AC边上相遇时,且PA=PB时,△PAE与△QBF全等.设此时PA=PB=x,
在Rt△PBC中,∵PB2=PC2+BC2,
∴x2=(8﹣x)2+62,
∵当P,Q在AC边上相遇,可得
解得
∴当v= cm/s时.t= 时,△PAE与△QBF全等.
【解析】【解答】解:(1)当AP=PC时,直线BP平分△ABC的面积.此时t=4.
故答案为4.
【分析】(1) 根据直线BP平分△ABC的面积进行解答即可;
(2)假设AQ=BP,利用勾股定理构建方程,进行解答并检验即可;
(3) 分两种情况,①当点Q在线段BC上时,②当P,Q在AC边上相遇时,且PA=PB时,△PAE与△QBF全等 ,据此分别解答即可.
一、单选题
1.下列图形中,不是轴对称图形的是( )
A. B. C. D.
2.如图,若 与 关于直线 对称, 交 于点 ,则下列说法中,不一定正确的是( )
A. B.
C. D.
3.下列四个图标中,属于轴对称图形的是( )
A. B. C. D.
4.在下列条件中,能确定 是直角三角形的条件有( )
A. B.
C. D.
5.柯桥区作为浙江省试点先行区,四年前就开始实行垃圾分类,以下是几种垃圾分类的图标,其中哪个几何图标是轴对称图形( )
A. B. C. D.
6.对于题目:如图, 是 的角平分线, 于点 ,若 ,求 的度数.下面是打乱了的解题过程:①∵ ;② ;③∵ 平分 ,∴ ;④∵ , ,则下列排序正确的是( ).
A.③④②① B.④②①③ C.③②④① D.③①④②
7.如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
8.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三个角的度数比为1:2:3 B.三条边的长度比为1:2:3
C.三条边满足关系a2+c2=b2 D.三个角满足关系∠B+∠C=∠A
9.下列各组数不是勾股数的是( )
A.2、3、4 B.3、4、5 C.6、8、10 D.5、12、13
10.如图,在△ABC中,AB=AC,AD,BE是△ABC的两条中线,P是AD上的一个动点,则下列线段的长等于CP+EP最小值的是( )
A.AC B.AD C.BE D.BC
二、填空题
11.如果一个直角二角形的两条直角边的长分别是5和12,那么这个直角三角形斜边长是 。
12.如图,A、B、C三点在同一条直线上,∠A=50°,BD垂直平分AE,垂足为D,则∠EBC的度数为 .
13.如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形):
14.如图,在△ABC中,∠BAD=∠B,∠EAC=∠C,BC=12,则△ADE的周长为 .
三、解答题
15.已知在中,,线段的垂直平分线交于点,交射线于点,连接.
(1)如图1,当点在边上时,若,求的度数;
(2)如图2,当点在延长线上时,设,用含的式子表示的度数
16.如图,△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.若∠B=40°,∠C=62°,请说明∠DAE的度数.
17.如图,每个小方格的边长都为.
(1)求图中格点四边形的面积;
(2)请探究:与的位置关系,并说明理由.
18.如图,在△ABC中,AB=AC,AD为BC边上的中线,∠CAD=40°,EF为过点A的一条直线,且EF∥BC,求∠BAE的度数.
四、综合题
19.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,EB平分∠DEC.
(1)求证:BC=CE;
(2)若CE=AB,EA=EB,求∠C的度数.
20.如图,在平面直角坐标系中完成下列各题:(不写作法,保留作图痕迹)
(1)在图一中作出△ABC关于y轴对称的△A1B1C1并写出A1、B1、C1的坐标.
(2)在图二中x轴上画出点P,使PA+PB的值最小.
21.已知a、b、c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数,①求c的长;
②判断△ABC的形状.
22.(1)如图1,长方体的长、宽、高分别为,,,如果用一根细线从点开始经过4个侧面缠绕一圈到达点,那么所用细线最短需要 ;
(2)如图2,长方体的棱长分别为,,假设昆虫甲从盒内顶点开始以的速度在盒子的内部沿棱向下爬行,同时昆虫乙从盒内顶点以相同的速度在盒内壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
23.如图,△ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从A点出发沿A→C→B路径以每秒1cm的运动速度向终点B运动;同时点Q从B点出发沿B→C→A路径以每秒vcm的速度向终点A运动.分别过P和Q作PE⊥AB于E,QF⊥AB于F.
(1)设运动时间为t秒,当t= 时,直线BP平分△ABC的面积.
(2)当Q在BC边上运动时(t>0),且v=1时,连接AQ、连接BP,线段AQ与BP可能相等吗?若能,求出t的值;若不能,请说明理由.
(3)当Q的速度v为多少时,存在某一时刻(或时间段)可以使得△PAE与△QBF全等.
答案解析部分
1.【答案】C
【解析】【解答】解:A、是轴对称图形,不符合题意;
B、是轴对称图形,不符合题意;
C 、是中心对称图形,不是轴对称图形,符合题意;
D、是轴对称图形,不符合题意.
故答案为:C.
【分析】 本题考查轴对称图形的概念. 轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
2.【答案】B
【解析】【解答】解:∵ 与 关于直线 对称,
∴ , , ,
故答案为:B.
【分析】根据轴对称的性质逐一判断即可.
3.【答案】B
【解析】【解答】解:A、不是轴对称图形,故此选项不符合题意;
B、是轴对称图形,故此选项符合题意;
C、不是轴对称图形,故此选项不符合题意;
D、不是轴对称图形,故此选项不符合题意.
故答案为:B.
【分析】将一个平面图形沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,根据轴对称图形的概念一一判断即可.
4.【答案】B
【解析】【解答】解:A、 ,
是等边三角形,故 选项不符合题意;
B、 ,
是直角三角形,故 选项 符合题意;
C、 ,
为最大角,
不是直角三角形;故 选项不符合题意;
D、 ,
所以不能判定 是直角三角形,
故 不符合题意,
故答案为:B.
【分析】确定三角形是直角三角形的条件是有一个角是直角,然后根据三角形的内角和定理分别进行解答并判断即可.
5.【答案】B
【解析】【解答】解:A、不是轴对称图形,故此选项错误;
B、是轴对称图形,故此选项正确;
C、不是轴对称图形,故此选项错误;
D、不是轴对称图形,故此选项错误.
故答案为:B.
【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,根据轴对称图形的定义,依次对各选项进行判断即可.
6.【答案】A
【解析】【解答】∵ 平分
∴
∵
∴
∴
∴
故答案为:A.
【分析】根据角平分线的性质,可得,利用垂直的定义得出,根据直角三角形两锐角互余得出 ,从而求出,据此判断即可.
7.【答案】A
【解析】【解答】解:∵AB的垂直平分线DE交AC于D,交AB于E,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∴∠CBD=∠ABD=36°,
即BD平分∠ABC;故①正确;
∴∠BDC=∠C=72°,
∴BC=BD,
∴BC=BD=AD,故②正确;
∴△BDC的周长为:BC+CD+BD=BC+CD+AD=AC+BC=AB+BC;故③正确;
∵CD<BD,
∴CD<AD,
∴D不是AC中点.故④错误.
故答案为:A.
【分析】由AB的垂直平分线DE交AC于D,交AB于E,可得AD=BD,即可求得∠ABD=∠A=36°,又由AB=AC,即可求得∠CBD=∠ABD=36°,∠BDC=∠C=72°,继而证得AD=BD=BC,△BDC的周长等于AB+BC.
8.【答案】B
【解析】【解答】解:A、三个角的度数比为1:2:3,最大角的度数是90°,是直角三角形,不符合题意;
B、三条边的比为1:2:3,12+22≠32,不是直角三角形,符合题意;
C、三条边满足关系a2+c2=b2,是直角三角形,不符合题意;
D、三个角满足关系∠B+∠C=∠A,所以∠A=90°,是直角三角形,不符合题意;
故答案为:B.
【分析】根据勾股定理的逆定理以及直角三角形的定义判断即可。
9.【答案】A
【解析】【解答】 解:A. 22+32≠42,故A选项不是勾股数;
B. 32+42=52,故B选项是勾股数;
C. 62+82=102 ,故C选项是勾股数;
D. 52+122=132,故D选项是勾股数;故选A.
10.【答案】C
【解析】【解答】解:如图,连接PB,
∵AB=AC,BD=CD,
∴AD⊥BC,
∴PB=PC,
∴PC+PE=PB+PE,
∵PE+PB≥BE,
∴P、B、E共线时,PB+PE的值最小,最小值为BE的长度,
故答案为:C.
【分析】如图连接PB,只要证明PB=PC,即可推出PC+PE=PB+PE,由PE+PB≥BE,可得P、B、E共线时,PB+PE的值最小,最小值为BE的长度.
11.【答案】13
【解析】【解答】
因为5 +12 =13
所以斜边等于13
【分析】考查勾股定理的性质;难题较低且属于常考题型。在直角三角形中,两直角边的平方和等于斜边的平方。注意求解出来的结果取的是正根
12.【答案】100°
【解析】【解答】∵BD垂直平分AE,
∴
∴
∴
故答案为100°.
【分析】根据线段垂直平分线的性质,得 根据等腰三角形的性质,得 再根据三角形外角的性质即可求解.
13.【答案】①③
【解析】【解答】答:由①③条件可判定△ABC是等腰三角形.
证明:∵∠EBO=∠DCO,∠EOB=∠DOC,(对顶角相等)
BE=CD,
∴△EBO≌△DCO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
【分析】根据已知条件求证△EBO≌△DCO,然后可得∠OBC=∠OCB再利用两角相等即可判定△ABC是等腰三角形.此题答案不唯一.
14.【答案】12
【解析】【解答】解:∵∠BAD=∠B,∠EAC=∠C,
∴AD=BD,AE=EC,
∴△ADE的周长=AD+DE+AE=BD+DE+EC=BC=12.
故答案是:12.
【分析】根据∠BAD=∠B,∠EAC=∠C,可得AD=BD,AE=EC,则△ADE的周长等于BC的长.
15.【答案】(1)解:垂直平分,
,
,
,
,
设,
在中,,
解得:,
;
(2)解:垂直平分,
,
,
,
,
设,
则,
在中,,
解得:,
∴.
【解析】【分析】(1)垂直平分线的性质的运用是解决本题的关键,利用其性质求得的等腰三角形AEC,进而得出底角相等∠C=∠EAC,利用等腰三角形的性质和三角形内角和定理就可以求得角的度数;
(2)类比(1)的思路进行求解即可.
16.【答案】解:∵ , ,
∴ ,
∵ 是 的平分线,
∴ ,
∵ 是 边上的高,
∴ 是直角三角形,
∴ ,
∴ .
【解析】【分析】先根据三角形内角和定理求∠BAC的度数,则可根据角平分线的定义求∠DAC,然后根据直角三角形的性质求出∠EAC,最后根据角的和差关系求∠DAE即可.
17.【答案】(1)解:,,
四边形的面积;
(2)解:由勾股定理,得,,
由题意可知,
,
为直角三角形,
,
.
【解析】【分析】(1)利用三角形的面积公式结合图形计算求解即可;
(2)利用勾股定理求出AD和CD的值,再求出△ACD为直角三角形,最后求解即可。
18.【答案】解:∵AB=AC, AD为BC边上的中线,
∴∠B=∠C,∠BAD=∠CAD=40°(三线合一),
∴∠BAC=∠BAD+∠CAD=80°,
∴,
∵EF∥BC,
∴∠BAE=∠B=50°.
【解析】【分析】根据等腰三角形的性质求出∠B=∠C,∠BAD=∠CAD,则可求出∠BAC的度数,然后根据等腰三角形的性质和三角形内角和定理求出∠B的度数,再根据平行线的性质求∠BAE度数即可.
19.【答案】(1)证明:∵EB平分∠DEC,
∴∠DEB=∠BEC.
∵DE∥BC.
∴∠DEB=∠EBC,
∴∠BEC=∠EBC,
∴BC=CE
(2)解:∵BC=CE,CE=AB,
∴BC=AB,
∴∠C=∠A,
设∠C=∠A=x,
∵EA=EB,
∴∠A=∠ABE=x,
∴∠EBC=∠BEC=∠A+∠ABE=2x,
∴2x+2x+x=180°,
∴∠C=x=36°
【解析】【分析】(1)根据角平分线以及平行线的性质:两直线平行内错角相等,即可得到∠BEC=∠EBC,再根据等腰三角形的判定,即可证明BC=CE.
(2)根据等腰三角形的性质:等腰三角形的两个底角相等,即可得到∠C=∠A,设∠A=∠C=x,又根据题意以及等腰三角形的性质可得∠A=∠ABE=x,根据三角形的任一外角等于与它不相邻的两个内角之和,再根据三角形的内角和为180°,即可列出方程,解出答案即可.
20.【答案】(1)解:如图一所示;
,
由图可知,A1(﹣1,2),B1(﹣3,1),C1(2,﹣1)
(2)解:如图二所示.
【解析】【分析】(1)画出各点关于y轴的对称点,再顺次连接并写出各点坐标即可;(2)作点A关于x轴的对称点A′,连接A′B交x轴于点P,则点P即为所求点.
21.【答案】(1)解:2<c<10;12<x<20
(2)解:①因为周长为小于18的偶数,所以x=16或x=14.
当x为16时,c=6;当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
【解析】【解答】解:(1)因为a=4,b=6,所以2<c<10.故周长x的范围为12<x<20
【分析】(1)根据三角形三边关系求出c的取值范围即可;
(2)①根据偶数的定义以及x的取值范围求出答案即可;
②利用等腰三角形的判定方法求出答案即可。
22.【答案】(1)
(2)解:设昆虫甲从顶点沿棱向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行,爬行捕捉到昆虫甲需x秒钟,
如图,在中,
∵长方体的棱长分别为,,
∴cm,cm,cm,cm,
∴,
解得:.
答:昆虫乙至少需要秒钟才能捕捉到昆虫甲.
【解析】【解答】解:(1)如图,将长方体展开,连接,
∵长方体的长、宽、高分别为,,,
∴这根细线最短的长为:m;
故答案为:.
【分析】(1)将长方体展开,连接AC,然后根据勾股定理计算即可求出这根细线最短的长;
(2)设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E→F爬行,爬行捕捉到昆虫甲需x秒钟,由题意可得AB=BC=6cm,AA1=14cm,AF=xcm,C1F=xcm,CF=(14-x)cm,AC=12cm,然后利用勾股定理求解即可.
23.【答案】(1)4
(2)解:假设可能相等.则有82+(6﹣t)2=62+(8﹣t)2,
解得t=0,不符合题意,
所以当Q在BC边上运动时(t>0),且v=1时、线段AQ与BP不可能相等.
(3)解:①当点Q在线段BC上时,
在Rt△AEP和Rt△BFQ中,
∵∠AEP=∠BFQ=90°,∠C=90°,
∴∠A+∠B=90°,∠B+∠BQF=90°,
∴∠A=∠BQF,
∴当PA=BQ时,△AEP≌△FQB,
∴当v=1cm/s时,0<t≤6时,△PAE与△QBF全等.
②当P,Q在AC边上相遇时,且PA=PB时,△PAE与△QBF全等.设此时PA=PB=x,
在Rt△PBC中,∵PB2=PC2+BC2,
∴x2=(8﹣x)2+62,
∵当P,Q在AC边上相遇,可得
解得
∴当v= cm/s时.t= 时,△PAE与△QBF全等.
【解析】【解答】解:(1)当AP=PC时,直线BP平分△ABC的面积.此时t=4.
故答案为4.
【分析】(1) 根据直线BP平分△ABC的面积进行解答即可;
(2)假设AQ=BP,利用勾股定理构建方程,进行解答并检验即可;
(3) 分两种情况,①当点Q在线段BC上时,②当P,Q在AC边上相遇时,且PA=PB时,△PAE与△QBF全等 ,据此分别解答即可.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
