浙教版七年级上册本册复习知识要点

陈云苗 七上数学复习教案 第 1 页
七上数学复习计划
周次 日 期 内 容
20 1.7—1.13 第1章《从自然数到有理数》 第2章《有理数的运算》
21 1.14—1.20 第3章《实数》 第4章《代数式》
22 1.21—1.27 第5章《一元一次方程》 第6章《数据与图表》
23 1.28—2.3 第7章《图形的初步认识》 《总复习》
第1章 从自然数到有理数
要点复习：
（1） 数轴：规定了原点、单位长度和正方向的直线叫做数轴。
（2） 相反数：实数与实数叫做互为相反数，零的相反数是零。
（3） 倒数：1除以一个非零实数的商，叫做这个实数的倒数，零没有倒数。
（4） 绝对值：正数的绝对值是它的本身；零的绝对值是零；
（5） 负数的绝对值是它的相反数。
（6） 整数和分数统称为有理数。
（7） 无尽不循环小数叫做无理数。
（8） 在数轴上，右边的点所表示的数总比左边的点所表示的数要大。
（9） 把一个数写成带有一位小数的数与10的整数次幂的积的形式，叫做科学记数法；
（10） 把由“四舍五入”法得到的近似数，从左边第一个不是零的数字起，到末位数字为止的所有数字，都叫做这个近似数的有效数字。
复习题：
1． 4 与4 有什么相同与不同之处？它们在数轴上的位置有什么关系？
分析：① 从数本身看来， 4 与4 只是符号不同；
② 从数轴上的位置来看，它们到原点的距离相等但方向不同。
师：向这样的一对数比较特殊，我们称其中一个数是另一个数的相反数。
定义：如果两个数只有符号不同，那么我们称其中一个数是另一个数的相反数。
也称这两个数互为相反数。
如： 2.5 的相反数是 100的相反数是
0.75的相反数是 0 的相反数是
2． 为相反数的两个数的特点：
3．回答下列问题
①一个数的绝对值是它本身，这个数是什么数？
②一个数的绝对值是它的相反数，这个数是什么数？
③一个数的绝对值一定是正数吗？
④一个数的绝对值不可能是负数，对吗？
⑤绝对值是同一个正数的数有两个，它们互为相反数，这句话对吗？
课后反思：
第2章 有理数的运算
要点复习：
（1） （2）
（3） （4）
（5） （6）
讲例题：
例1．如果两个数的和是正数，那么这两个数一定（ ）
　　（A）都是正数　　　　 　　（B）只有一个正数
　　（C）至少有一个是正数　　 （D）以上答案都不对
　　例2．计算：
　 例3．计算： 　
　例4．计算：
　例5 计算： 　
练习题：
　1．计算：
　2． 计算：
　　（1）34；（2）－34；（3）（－3）4；（4） ；（5） ；（6） 　
　3． 计算：
　
课后反思：
第3章 实 数
复习要点：
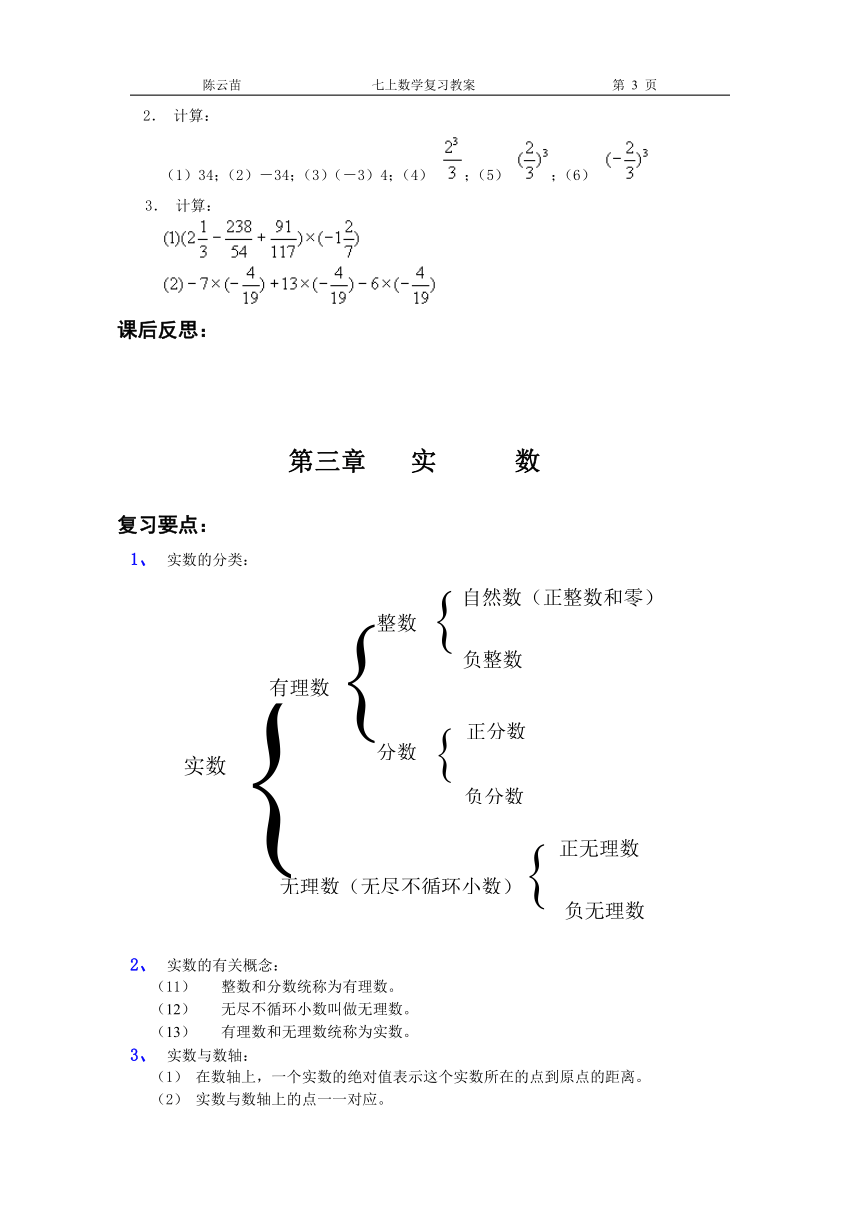
1、 实数的分类：
2、 实数的有关概念：
（11） 整数和分数统称为有理数。
（12） 无尽不循环小数叫做无理数。
（13） 有理数和无理数统称为实数。
3、 实数与数轴：
（1） 在数轴上，一个实数的绝对值表示这个实数所在的点到原点的距离。
（2） 实数与数轴上的点一一对应。
（3） 在数轴上，右边的点所表示的数总比左边的点所表示的数要大。
讲例题：
例1（由学生板演）：① 原式=
② 原式=
例2．计算：① （精确到0.001）
② （结果保留4个有效数字）
生：先练习，再同桌交流计算结果。
师：写出解题的规范化：
① 按键顺序： 8 － 9 =
0.748343301
②
例3．计算： （精确到0.01）
解：原式=
=
==18.94427197
练习题：
1． 计算：① （精确到0.01）
② （结果保留3个有效数字）
③ （精确到0.01）
2． （结果保留3个有效数字）
3．计算：＿＿ ； ＿＿ ； ＿＿
利用计算器计算：＿＿＿ （精确到0.01） ＿＿＿ （保留3个有效数字）
＿＿＿ （精确到万分位） ＿＿＿ （精确到0.01）
＿＿＿ （保留2个有效数字）
课后反思：
第4章 代数式
复习要点：
1、 乘法公式：
（1） 平方差公式：
（2） 完全平方公式：
（3） 完全平方公式：
（4） 多项式乘法公式：
（5） 立方和公式：
（6） 立方差公式：
2、 平方根的定义：如果一个数的平方等于，那么这个数就是的平方根（也叫做二次方根）。记作：。
3、 平方根的性质：一个正数有正、负两个平方根，它们互为相反数；零的平方根是零；负数没有平方根。
4、 算术平方根的定义：正数正的平方根和零的平方根，统称为算术平方根。非负数的算术平方根记作：，且。
5、 立方根的定义：如果一个数的立方等于，那么这个数就是的立方根（也叫做三次方根）。记作：。
讲例题：
题型一 数学与生产实际
例1 窗户的形状如图所示，其上部是半圆形，下部是边长相同的四个小正方形，已知下部正方形的边长为acm，计算：
（1）窗的面积；（不考虑窗框的宽度） （2）窗框的总长。
题型二 数学与生活
例2 某企业去年的年产值为a亿元，今年比去年增长了10%。如果明年还能按这个速度增长，请你预测一下，该企业明年的年产值能达到多少亿元？
如果去年的年产值是2亿元，那么预计明年的年产值是多少亿元？
（1）去年年产值是----------------------亿元；
（2）今年年产值是----------------------亿元；
（3）如果明年还能按这个速度增长，那么明年的产值是-----------------。
解：由题意可得：今年的年产值为----------------------亿元，
于是明年的年产值为 亿元，若去年的年产值为2亿元，则明年的年产值为--------（亿元）.
答：该企业明年的年产值将能达到1.21a亿元。由去年的年产值是2亿元，可以预测明年的年产值是2.42亿元。
题型三 拓展创新
例3 研究下列算式，你会发现什么规律？
1×3+1=4=22 ， 2×4+1=9=32 ， 3×5+1=16=42 ， 4×6+1=25=52 ，…
将你找出的规律用代数式表示出来：————
练习题：
练习1： 列代数式表示某种数量
（1）有两个连续整数，若n表示较小的整数，则另一个整数是＿＿＿
（２）一个长方形的长、宽分别为 m ,n ;则这个长方形的周长是＿＿，面积是＿＿＿＿＿＿．
（３）有一个个位数是５的两位数表示为10a+5 ,则a表示＿＿＿＿．
（4）我国政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品原价为a元,在1999年涨价20%后,2001年又降价60%,这种药品降价后的价格为---------------。
（5）如图三角形的周长L=_________ 面积S=_______
（6）如图半径为r的圆的周长L=________ 面积S=________
（7）如图边长a为的正方形的周长L=_____ 面积S=_____
（8）如图长为a，宽为b的矩形的周长L=______ 面积S=______
练习2： 代数式求值
1.当x=3 时，求代数式2x2-x-1的值。
2.设x+y=5,xy=-3，求(2x-3y-2xy)-(x-4y+xy)的值。
3.已知：当x=-2时，代数式ax3+bx-7的值是5，那么当x=2时，求代数式ax3+bx-7的值。
练习3： 利用去括号，合并同类项进行整式的运算
先化简，再求值。
1/2X-2(x- 1/3y2)+(-3/2x+1/3y2)，其中x=-2，y=2/3。
注意：1.在涉及代数式的求值问题中，总是要先化简，再求值，从而运算量降低。
2.代入求值时，要适当添加括号。
3.求值时，要注意式中的同一字母必须用同一数值去代替，式中原有的数字和运算符号都不能改变。
课后反思：
第5章 一元一次方程
要点复习：
1．只含有一个未知数，并且未知数的次数是一次的整式方程叫做一元一次方程
2．解一元一次方程的一般步骤是：
（1）去分母（2）去括号（3）移项（4）合并同类项（5）将未知数的系数化为“1”
3．一元一次方程ax=b的解的情况：
（1）当a≠0时，ax=b有唯一的解
（2）当a=0，b≠0时，ax=b无解
（3）当a=0，b=0时，ax=b有无穷多个解
1．列一元一次方程解应用题，必须认真做到“设、列、解、验、答”五个步骤：
“设”――审清题意，明确等量关系，恰当地设立未知数来表示某个未知量。
“列”——根据问题中的等量关系列出方程。
“解”——解方程。检验方程的解，并判断方程的解是否应用题的实际意义。
“验”——双重检验，检验根的正确性，检验解的合理性
“答”——写出应用题的答案。
2．应用题中常见的基本关系式：
（1）行程问题：路程=速度时间
（2）工程问题：工作量=工作效率时间
练习题：
1．有两个工程队，第一队有46人，第二队有28人，从第一队调x人到第二队使两队人数相等， 列方程得：________________________________________
2．一项工程，甲队单独做10天可以完成，乙队单独做15天可以完成，两队合作x天可以完成， 列方程得：________________________________________
3．某汽车厂今年生产汽车16000辆，去年生产x辆，今年比去年生产的汽车增加1倍还多1000辆， 列方程得：________________________________________
4．某车间接到x件零件加工任务，计划每天加工120件，可以如期完成，而实际加工每天多做40件，结果提前6天完成，列方程得：___________________________________
5．将5千克浓度为85%的农药配成浓度为2%的药水杀虫，应该加水x千克
列方程得：________________________________________
6．甲、乙两车工在一天内共加工零件180个，其中甲车工加工x件，乙车工完成的件数是甲车工的， 列方程得：________________________________________
7．收割一块小麦，第一组需要5小时收割完，第二组需要7小时收割完。第一组收割1小时后再增加第二组一起收割，两组共同收割完用了x小时
列方程得：________________________________________
8．正方形边长为x米，将它的一边减少1.2米，另一边减少1.5米，所得到的矩形面积比正方形面积减少14.4平方米， 列方程得：________________________________________
二、分析应用题
1．甲、乙两站相距240千米，客车每小时行65千米，货车每小时行35千米。货车从甲站开往乙站1小时后，客车从乙站开往甲站，货车开出后x小时两车相遇.
列表分析
速度 时间 路程 相等关系
货车
客车
2．要配制浓度为10%的硫酸溶液980千克，需要用x千克浓度为98%的硫酸溶液
列表分析
浓度 溶液 溶质 相等关系
配制硫酸
原硫酸
三、填空题
1．两数之和是a，其中一个数是x，那么这两个数之积是__________________________
2．a是一个两位数，b是一个一位数，若把b放在a的右边，这个三位数是_________________
3．梯形下底是a，上底是下底的，高比下底小7，那么梯形的面积是__________________
4．刘庄、王湾两村合修一个小型水库，按受益面积3：5分担建筑费用a万元，那么刘庄应承担____________万元，王湾应承担_________________万元
四、列方程解应用题
1．我国四大发明之一的黑火药，它所用的原料硝酸钾、硫磺、木炭的重量比是15：2：3，要配制这种火药160千克，问三种原料应各取多少克？
2．A、B两城相距200千米，客车在A城，速度为每小时40千米，吉普车在B城，速度为每小时60千米，两车同时相向而行，问经过多少小时相遇？
3．某学校同学参加绿化植树活动，松树、柏树和柳树共栽了900棵，其中柏树是松树的2倍，柳树是柏树的3倍，问松树、柏树和柳树各栽了多少棵？
课后反思：
第6章 数据与图表
复习要点：
1、 常用统计图有：折线形统计图、条形统计图、圆形统计图．
2、 几个基本概念：
（1） 我们要考察的对象的全体叫做总体。
（2） 其中每个考察的对象叫做个体。
（3） 从总体中抽取的一部分个体的集体叫做总体的一个样本。
（4） 样本中的个体数目叫做样本容量。
（5） 总体中所有个体的平均数叫做总体平均数。
（6） 样本中所有个体的平均数叫做样本平均数，
（7） 通常我们用样本平均数去估计总体平均数。
3、 平均数的计算：
（1） 利用定义计算：如果有n个数x1,x2,x3,…，xn，那么＝(x1+x2+x3+…+xn),叫做这n个数的平均数。
（2） 利用加权平均数公式计算：＝(x1f1+x2f2+x3f3+…+xkfk)其中n=f1+f2+f3+…+fk
（3） 利用基准数A进行计算：＝A＋
复习题：
1．知道北京2008奥运会的三大主题吗？
“绿色奥运”、“人文奥运”、 “科技奥运”， 其中“绿色奥运”是第26届奥运会悉尼能够夺得举办权的一个重要口号，而且他们实践了这一点，这说明奥运会对环境质量的要求很高。“绿色”的一个重要方面是：空气质量达到优或良的天数必须占62％以上
2．用什么来衡量城市空气质量的优劣呢？城市空气质量通常用污染指数W 衡量。若W小于或等于50，空气质量为优；若W大于50且小于或等于100，空气质量为良；若W大于100且小于或等于150，空气质量为轻度污染。
3．近年北京的环境在综合治理下不断进步。现有一张北京2004年5月空气污染指数统计表，根据这张表格能否判断北京市目前的空气质量是否达到“绿色奥运”的标准？
北京市2004年5月空气污染指数统计表
制表日期：2004年6月20号
污染指数（W） 40 70 90 110 120 140
天数（t） 3 5 10 1 4 7
4．先让大家欣赏一个扇形统计图。（展示）同学们暑假肯定看了奥运会，能知道中国得了多少枚金牌吗？射击 4 12.5%
球类 8 25%
水上项目 8 25%
力量型项目 9 28.125%
田径 2 6.25%
体操 1 3.125%
从这个统计图中同学们能知道中国在什么项目上有优势，什么项目上薄弱呢？大家知道吗？美国在什么项目上有优势？
练习题：SMJ上的题。
课后反思：
第7章 图形的初步知识
要点复习：
1、 线段、射线与直线：
（1） 线段与射线都是直线的一部分，线段有两个端点，射线只有一个端点，直线没有端点。
（2） 两点确定一条直线；两点之间线段最短。
（3） 在点到直线上各点的连线段中，垂线段最短。
2、 角的有关概念：
（4） 角可以分为：锐角（小于90度的角）；直角（90度的角）；纯角（大于90度而小于180度的角）；平角（180度的角）；周角（360度的角）
（5） 两个角的和是90度，叫做两个角互余；两个角的和是180度叫做两个角互补。
（6） 同角的余角相等；同角的补角相等。
3、 相交线的性质：
（1） 对顶角相等。
（2） 两直线相交只有一个交点。
4、 平行线的定义：在同一平面内，两条永不相交的直线叫做平行线。
复习题：
1．试用适当的方法表示下列图中的每个角：
（1） （2）
2、从角的运动定义出发，得到平角、周角的定义。
平角 周角
图7-23
（注：没有特别说明，本书只讨论大于0°且小于180°的角）
3．观察图7-24中的量角器，并讨论下列问题：
（1）量角器上的平角被分成多少个1°的角？
（2）先估计图7-25中，∠A和∠B的度数，再用量角器量一量，在测量中，你遇到哪些问题？
在测量角时，有时以度为单位还不够，我们需要用比1°更小的单位，称之为分和秒，把1°的角等分成60份，每一份是1分，记做1'，把1分的角再等分成60份，每份就是1秒，记做1"，
即1°=60' 1'=()° 1周角=360° 1'=60" 1"=()' 1平角=180°
4、用度、分、秒表示：48.32° 用度表示：30°9'36" 计算：180°－(45°17'＋52°57')
课后反思：
A
B
B
O
(B)
A
O
A
C
B
平角
钝角
直角
锐角
实数
有理数
整数
分数
无理数（无尽不循环小数）
自然数（正整数和零）
负整数
正分数
负分数
正无理数
负无理数