26.2.2 二次函数y=ax^2+bx+c的图象与性质(共30张PPT)
文档属性
| 名称 | 26.2.2 二次函数y=ax^2+bx+c的图象与性质(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
二次函数y=+bx+c的图象与性质
华师大·九下
数学的真谛就在于不断寻求用越来越简单的方法证明定理和解决数学问题. ——加德纳
26.2.2
1. 亲爱的同学们,上节课我们学习了y=ax2 (a≠0)的图象和性质,请同学们回忆一下当a>0, a<0时函数的具体性质?
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2
y= -ax2
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
我们已经研究了的图象和y=ax2 (a≠0)
性质 现在我们来研究一般的问题
活动探究:思考以下问题,动手画一画。
研究二次函数 的图象.
y=+1
这个二次函数的关系式比 复杂些,它与 之间有什么联系?
2
y=+1
如果将函数关系式配方呢?
回想上学期的换元法?
y=+1
解:设x-2=m
则原式变形为,
y=+1
01.二次函数y=的图象与性质
02.二次函数y=的图象与性质
知
识
点
01
二次函数y=+k的
图象的与性质
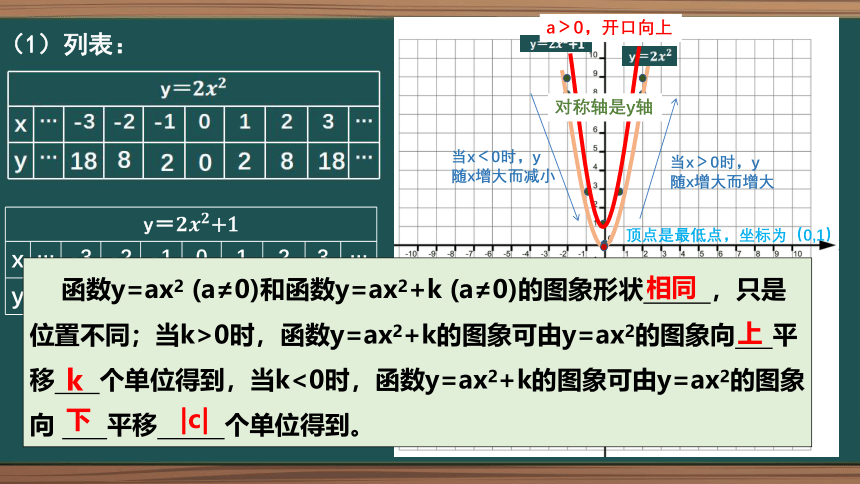
(1)列表:
y=+1 x … -3 -2 -1 0 1 2 3 …
y … …
19
9
3
1
3
9
19
a>0,开口向上
对称轴是y轴
当x<0时,y
随x增大而减小
当x>0时,y
随x增大而增大
顶点是最低点,坐标为(0,1)
函数y=ax2 (a≠0)和函数y=ax2+k (a≠0)的图象形状 ,只是位置不同;当k>0时,函数y=ax2+k的图象可由y=ax2的图象向 平移 个单位得到,当k<0时,函数y=ax2+k的图象可由y=ax2的图象向 平移 个单位得到。
相同
上
k
下
|c|
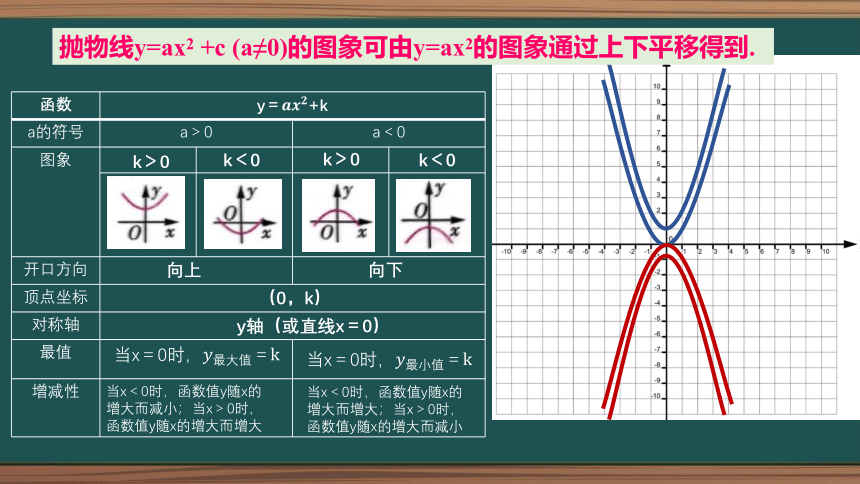
函数 y=+k a的符号 a>0 a<0 图象
开口方向 顶点坐标 对称轴 最值 增减性
k>0
k<0
k>0
k<0
向上
向下
(0,k)
y轴(或直线x=0)
当x=0时,=k
当x=0时,=k
当x<0时,函数值y随x的增大而减小;当x>0时,函数值y随x的增大而增大
当x<0时,函数值y随x的增大而增大;当x>0时,函数值y随x的增大而减小
抛物线y=ax2 +c (a≠0)的图象可由y=ax2的图象通过上下平移得到.
y=
向上平移
k 个单位
y=
向下平移
|k|个单位
y=
“上加下减”
课堂练习
填空:
1. 把抛物线 向下平移2个单位,可以得到抛物线 ,再向上平移5个单位,可以得到抛物线 ;
2. 对于函数y= –x2+5,
当x 时,函数值y随x的增大而增大;
当x 时,函数值y随x的增大而减小;
当x 时,函数取得最 值,为 。
<0
>0
=0
大
5
3. 函数y=ax2-a与y= 在同一直角坐标系中的图象可能是 ( )
(a≠0)
A
02
二次函数y=的图象与性质
函数 开口方向 对称轴 顶 点坐 标 Y的最值 增减性 在对称轴左侧 在对称轴右侧
y=ax2 a>0
a<0
y=ax2+k a>0
a<0
向上
向下
向上
向下
Y轴
Y轴
Y轴
Y轴
(0,0)
(0,0)
(0,k)
(0,k)
最小值是0
最大值是0
最小值是k
最大值是k
Y随x的增大而增大
Y随x的增大而减小
Y随x的增大而减小
Y随x的增大而增大
Y随x的增大而减小
Y随x的增大而增大
Y随x的增大而增大
Y随x的增大而减小
思考:函数的图象,能否也可以由函数平移得到?
(1)列表:
2
y= x … -3 -2 -1 0 1 2 3 …
y … 50 32 18 8 2 0 2 …
根据所画图象,填写下表:
抛物线 开口方向 对称轴 顶点坐标
向上
向上
y轴
x=2
(0,0)
(2,0)
通过图象,发现两条抛物线有何异同点
因为a相同,所以两条抛物线的开口方向,形状大小相同.
但上表可发现它们顶点和对称轴不同,也就是位置不同.
那同学们思考下,它们的位置有何关联呢?
新知讲解
函数y=(x-2)2的图象与y=x2的图象的位置有什么关系
函数y=(x-2)2的图象可由 y=x2的图象沿x轴向右平移2个单位长度得到.
x
y
-4
-3
-2
-1
o
1
2
3
4
1
2
3
4
5
6
图象是轴对称图形
对称轴是平行于
y轴的直线:x=2.
顶点坐标
是点(2,0).
(1)列表:
2
y= x … -3 -2 -1 0 1 2 3 …
y … 2 0 2 8 18 32 50 …
练一练
在同一平面直角坐标系内画出下列二次函数的图象:
x
y
1.说上述函数的开口方向,对称轴及顶点坐标;
2.结合图象,指出上述函数的性质及相互关系.
练一练
x
y
抛物线 开口方向 对称轴 顶点坐标
向下
直线x=-1
( -1 , 0 )
直线x=0
直线x=1
向下
向下
( 0 , 0 )
( 1, 0)
思考:通过上述例子,函数y=a(x-h)2的性质是什么?
函数 y= a的符号 a>0 a<0 图象
开口方向 顶点坐标 对称轴 最值 增减性 h>0
h<0
h>0
h<0
向上
向下
(h,0)
x=h
当x=h时,y最小= 0
当x=h时,y最大= 0
在对称轴左侧(x<h),y随x的增大而减小;在对称轴左侧(x>h),y 随x的增大而增大.
在对称轴左侧(x<h),y随x的增大而增大;在对称轴左侧(x>h), y 随x的增大而减小.
做一做
在同一直角坐标系中,画出二函数 y=x2与y=(x+1)2的图象.
解:先列表:
x ··· -3 -2 -1 0 1 2 3 ···
··· 2 0 2 ···
··· 2 0 2 8 ···
··· 8 2 0 2 ···
函数图象如下
x
y
-4
-3
-2
-1
o
1
2
3
4
1
2
3
4
5
6
做一做
在同一直角坐标系中,画出二函数 y=x2与y=(x+1)2的图象.
解:
抛物线 y=(x+1)2,y=(x-1)2与抛物线y=x2 有什么关系?
可以发现,把抛物线y=x2 向 平移1个单位长度,就得到抛物线 ;把抛物线 y=x2 向 平移1个单位长度,就得到抛物线 .
右
左
y=
向上平移
k 个单位
y=
向下平移
k个单位
y=
“上加下减”
向左平移
h个单位
y=a(x+h)2
向右平移
h个单位
y=a(x-h)2
“左加右减”
课堂练习
填空:
1. 把抛物线y=-x2沿着x轴方向平移3个单位长度,那么平移后抛物线的解析式是 .
2.若抛物线y=-x2向左平移2个单位,所得抛物线的解析式是_______________
y=-(x+3)2或y=-(x-3)2
3. 在平面直角坐标系中,二次函数y=a(x-h)2(a≠0)的图象可能是( )
4. 顶点是(-3,0),开口方向、形状与函数y=x2的图象相同的抛物线对应的表达式为( )
A.y=(x-3)2 B.y=(x+3)2
C.y=-(x+3)2 D.y=-(x-3)2
D
B
3.已知A(-4,y1),B (1,y2)两点都在二次函数y=-3(x+1)2的图象上,则y1,y2的大小关系为________.
4.将函数y=x2的图象向右平移a(a>0)个单位,得到函数y=(x-4)2的图象,则a的值为________.
y1<y2
4
二次函数y=+bx+c的图象与性质
华师大·九下
数学的真谛就在于不断寻求用越来越简单的方法证明定理和解决数学问题. ——加德纳
26.2.2
1. 亲爱的同学们,上节课我们学习了y=ax2 (a≠0)的图象和性质,请同学们回忆一下当a>0, a<0时函数的具体性质?
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2
y= -ax2
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
我们已经研究了的图象和y=ax2 (a≠0)
性质 现在我们来研究一般的问题
活动探究:思考以下问题,动手画一画。
研究二次函数 的图象.
y=+1
这个二次函数的关系式比 复杂些,它与 之间有什么联系?
2
y=+1
如果将函数关系式配方呢?
回想上学期的换元法?
y=+1
解:设x-2=m
则原式变形为,
y=+1
01.二次函数y=的图象与性质
02.二次函数y=的图象与性质
知
识
点
01
二次函数y=+k的
图象的与性质
(1)列表:
y=+1 x … -3 -2 -1 0 1 2 3 …
y … …
19
9
3
1
3
9
19
a>0,开口向上
对称轴是y轴
当x<0时,y
随x增大而减小
当x>0时,y
随x增大而增大
顶点是最低点,坐标为(0,1)
函数y=ax2 (a≠0)和函数y=ax2+k (a≠0)的图象形状 ,只是位置不同;当k>0时,函数y=ax2+k的图象可由y=ax2的图象向 平移 个单位得到,当k<0时,函数y=ax2+k的图象可由y=ax2的图象向 平移 个单位得到。
相同
上
k
下
|c|
函数 y=+k a的符号 a>0 a<0 图象
开口方向 顶点坐标 对称轴 最值 增减性
k>0
k<0
k>0
k<0
向上
向下
(0,k)
y轴(或直线x=0)
当x=0时,=k
当x=0时,=k
当x<0时,函数值y随x的增大而减小;当x>0时,函数值y随x的增大而增大
当x<0时,函数值y随x的增大而增大;当x>0时,函数值y随x的增大而减小
抛物线y=ax2 +c (a≠0)的图象可由y=ax2的图象通过上下平移得到.
y=
向上平移
k 个单位
y=
向下平移
|k|个单位
y=
“上加下减”
课堂练习
填空:
1. 把抛物线 向下平移2个单位,可以得到抛物线 ,再向上平移5个单位,可以得到抛物线 ;
2. 对于函数y= –x2+5,
当x 时,函数值y随x的增大而增大;
当x 时,函数值y随x的增大而减小;
当x 时,函数取得最 值,为 。
<0
>0
=0
大
5
3. 函数y=ax2-a与y= 在同一直角坐标系中的图象可能是 ( )
(a≠0)
A
02
二次函数y=的图象与性质
函数 开口方向 对称轴 顶 点坐 标 Y的最值 增减性 在对称轴左侧 在对称轴右侧
y=ax2 a>0
a<0
y=ax2+k a>0
a<0
向上
向下
向上
向下
Y轴
Y轴
Y轴
Y轴
(0,0)
(0,0)
(0,k)
(0,k)
最小值是0
最大值是0
最小值是k
最大值是k
Y随x的增大而增大
Y随x的增大而减小
Y随x的增大而减小
Y随x的增大而增大
Y随x的增大而减小
Y随x的增大而增大
Y随x的增大而增大
Y随x的增大而减小
思考:函数的图象,能否也可以由函数平移得到?
(1)列表:
2
y= x … -3 -2 -1 0 1 2 3 …
y … 50 32 18 8 2 0 2 …
根据所画图象,填写下表:
抛物线 开口方向 对称轴 顶点坐标
向上
向上
y轴
x=2
(0,0)
(2,0)
通过图象,发现两条抛物线有何异同点
因为a相同,所以两条抛物线的开口方向,形状大小相同.
但上表可发现它们顶点和对称轴不同,也就是位置不同.
那同学们思考下,它们的位置有何关联呢?
新知讲解
函数y=(x-2)2的图象与y=x2的图象的位置有什么关系
函数y=(x-2)2的图象可由 y=x2的图象沿x轴向右平移2个单位长度得到.
x
y
-4
-3
-2
-1
o
1
2
3
4
1
2
3
4
5
6
图象是轴对称图形
对称轴是平行于
y轴的直线:x=2.
顶点坐标
是点(2,0).
(1)列表:
2
y= x … -3 -2 -1 0 1 2 3 …
y … 2 0 2 8 18 32 50 …
练一练
在同一平面直角坐标系内画出下列二次函数的图象:
x
y
1.说上述函数的开口方向,对称轴及顶点坐标;
2.结合图象,指出上述函数的性质及相互关系.
练一练
x
y
抛物线 开口方向 对称轴 顶点坐标
向下
直线x=-1
( -1 , 0 )
直线x=0
直线x=1
向下
向下
( 0 , 0 )
( 1, 0)
思考:通过上述例子,函数y=a(x-h)2的性质是什么?
函数 y= a的符号 a>0 a<0 图象
开口方向 顶点坐标 对称轴 最值 增减性 h>0
h<0
h>0
h<0
向上
向下
(h,0)
x=h
当x=h时,y最小= 0
当x=h时,y最大= 0
在对称轴左侧(x<h),y随x的增大而减小;在对称轴左侧(x>h),y 随x的增大而增大.
在对称轴左侧(x<h),y随x的增大而增大;在对称轴左侧(x>h), y 随x的增大而减小.
做一做
在同一直角坐标系中,画出二函数 y=x2与y=(x+1)2的图象.
解:先列表:
x ··· -3 -2 -1 0 1 2 3 ···
··· 2 0 2 ···
··· 2 0 2 8 ···
··· 8 2 0 2 ···
函数图象如下
x
y
-4
-3
-2
-1
o
1
2
3
4
1
2
3
4
5
6
做一做
在同一直角坐标系中,画出二函数 y=x2与y=(x+1)2的图象.
解:
抛物线 y=(x+1)2,y=(x-1)2与抛物线y=x2 有什么关系?
可以发现,把抛物线y=x2 向 平移1个单位长度,就得到抛物线 ;把抛物线 y=x2 向 平移1个单位长度,就得到抛物线 .
右
左
y=
向上平移
k 个单位
y=
向下平移
k个单位
y=
“上加下减”
向左平移
h个单位
y=a(x+h)2
向右平移
h个单位
y=a(x-h)2
“左加右减”
课堂练习
填空:
1. 把抛物线y=-x2沿着x轴方向平移3个单位长度,那么平移后抛物线的解析式是 .
2.若抛物线y=-x2向左平移2个单位,所得抛物线的解析式是_______________
y=-(x+3)2或y=-(x-3)2
3. 在平面直角坐标系中,二次函数y=a(x-h)2(a≠0)的图象可能是( )
4. 顶点是(-3,0),开口方向、形状与函数y=x2的图象相同的抛物线对应的表达式为( )
A.y=(x-3)2 B.y=(x+3)2
C.y=-(x+3)2 D.y=-(x-3)2
D
B
3.已知A(-4,y1),B (1,y2)两点都在二次函数y=-3(x+1)2的图象上,则y1,y2的大小关系为________.
4.将函数y=x2的图象向右平移a(a>0)个单位,得到函数y=(x-4)2的图象,则a的值为________.
y1<y2
4
