26.2.1 二次函数y=ax^2的图象与性质(共18张PPT)
文档属性
| 名称 | 26.2.1 二次函数y=ax^2的图象与性质(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 20:00:04 | ||
图片预览






文档简介
(共18张PPT)
26.2.1 二次函数y=的图象与性质
华师大·九下
数学的真谛就在于不断寻求用越来越简单的方法证明定理和解决数学问题. ——加德纳
1. 亲爱的同学们,上节课我们学习了二次函数的定义,什么是二次函数呢?
形如y=ax2+bx+c (a,b,c是常数,a≠0)的函数叫做x的二
次函数。a为二次项系数,b为一次项系数,
c为常数项
01.二次函数y=的图象的画法
02.二次函数y=的图象与性质
知
识
点
01
二次函数y=的
图象的画法
我们知道,一次函数的图象是一条直线。那么,二次函数的图象是什么?它有什么特点?反映了二次函数的哪些性质?
2. 在研究一次函数时,曾借助图象了解了一次函数的性质。怎样画函数的图象呢?
列表
描点
连线
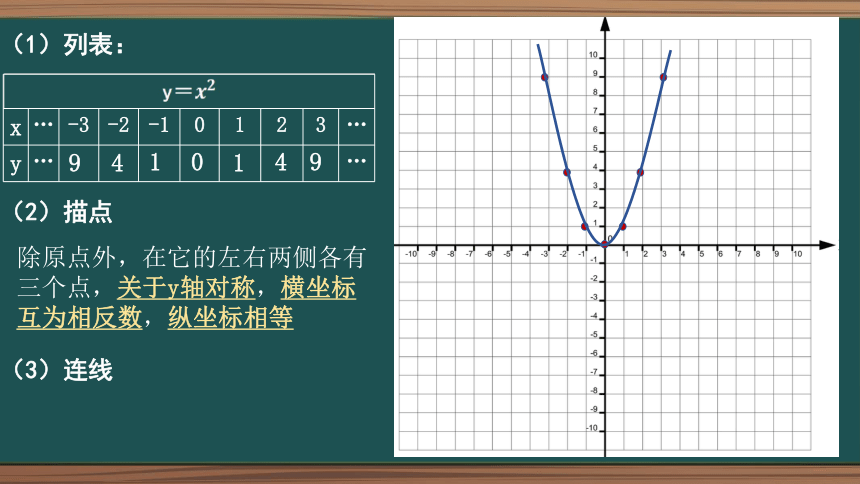
(1)列表:
(2)描点
除原点外,在它的左右两侧各有三个点,关于y轴对称,横坐标互为相反数,纵坐标相等
(3)连线
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
1.二次函数y=的图象是一条经过原点,以y轴为对称轴的抛物线,也称抛物线y=. 抛物线与它的对称轴的交点叫做抛物线的顶点.
顶点
02
二次函数y=的
图象与性质
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y=- x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
0
-1
-4
-9
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y=- x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
0
-1
-4
-9
关于x轴对称
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y=- x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
0
-1
-4
-9
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y=- x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
0
-1
-4
-9
a>0,开口向上
a<0,开口向下
当x<0时,y
随x增大而减小
当x>0时,y
随x增大而增大
对称轴是y轴
当x<0时,y
随x增大而增大
当x>0时,y
随x增大而减小
对称轴是y轴
顶点是最低点,坐标为(0,0)
顶点是最高点,坐标为(0,0)
函数 y= a的符号 a>0 a<0
图象
开口方向 向上 向下
顶点坐标 (0,0) 对称轴 y轴(或直线x=0) 最值 当x=0时,=0 当x=0时,=0
增减性 当x<0时,函数值y随x的增大而减小;当x>0时,函数值y随x的增大而增大 当x<0时,函数值y随x的增大而增大;当x>0时,函数值y随x的增大而减小
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y= x … -3 -2 -1 0 1 2 3 …
y … …
18
8
2
0
2
8
18
y= x … -3 -2 -1 0 1 2 3 …
y … …
2
0
2
(1)列表:
2
0
2
开口从小到大的排序
a越大,开口越小
(1)列表:
y=- x … -3 -2 -1 0 1 2 3 …
y … …
y=-2 x … -3 -2 -1 0 1 2 3 …
y … …
y=- x … -3 -2 -1 0 1 2 3 …
y … …
a越大,开口越大
因为开口向下,a为负数,所以|a|越大,开口越小
课堂练习
填空:
(1)抛物线y=-9x2的顶点坐标是___________; 对称轴是________;
在_____________ 侧,y随着x的增大而增大;
在______________侧,y随着x的增大而减小;
当x=_______时,函数y的值最大,最大值是________;
抛物线y=-9x2在x轴的________方(除顶点外).
(0,0)
y轴
对称轴的左
对称轴的右
0
0
下
26.2.1 二次函数y=的图象与性质
华师大·九下
数学的真谛就在于不断寻求用越来越简单的方法证明定理和解决数学问题. ——加德纳
1. 亲爱的同学们,上节课我们学习了二次函数的定义,什么是二次函数呢?
形如y=ax2+bx+c (a,b,c是常数,a≠0)的函数叫做x的二
次函数。a为二次项系数,b为一次项系数,
c为常数项
01.二次函数y=的图象的画法
02.二次函数y=的图象与性质
知
识
点
01
二次函数y=的
图象的画法
我们知道,一次函数的图象是一条直线。那么,二次函数的图象是什么?它有什么特点?反映了二次函数的哪些性质?
2. 在研究一次函数时,曾借助图象了解了一次函数的性质。怎样画函数的图象呢?
列表
描点
连线
(1)列表:
(2)描点
除原点外,在它的左右两侧各有三个点,关于y轴对称,横坐标互为相反数,纵坐标相等
(3)连线
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
1.二次函数y=的图象是一条经过原点,以y轴为对称轴的抛物线,也称抛物线y=. 抛物线与它的对称轴的交点叫做抛物线的顶点.
顶点
02
二次函数y=的
图象与性质
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y=- x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
0
-1
-4
-9
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y=- x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
0
-1
-4
-9
关于x轴对称
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y=- x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
0
-1
-4
-9
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y=- x … -3 -2 -1 0 1 2 3 …
y … …
-9
-4
-1
0
-1
-4
-9
a>0,开口向上
a<0,开口向下
当x<0时,y
随x增大而减小
当x>0时,y
随x增大而增大
对称轴是y轴
当x<0时,y
随x增大而增大
当x>0时,y
随x增大而减小
对称轴是y轴
顶点是最低点,坐标为(0,0)
顶点是最高点,坐标为(0,0)
函数 y= a的符号 a>0 a<0
图象
开口方向 向上 向下
顶点坐标 (0,0) 对称轴 y轴(或直线x=0) 最值 当x=0时,=0 当x=0时,=0
增减性 当x<0时,函数值y随x的增大而减小;当x>0时,函数值y随x的增大而增大 当x<0时,函数值y随x的增大而增大;当x>0时,函数值y随x的增大而减小
(1)列表:
y= x … -3 -2 -1 0 1 2 3 …
y … …
9
4
1
0
1
4
9
y= x … -3 -2 -1 0 1 2 3 …
y … …
18
8
2
0
2
8
18
y= x … -3 -2 -1 0 1 2 3 …
y … …
2
0
2
(1)列表:
2
0
2
开口从小到大的排序
a越大,开口越小
(1)列表:
y=- x … -3 -2 -1 0 1 2 3 …
y … …
y=-2 x … -3 -2 -1 0 1 2 3 …
y … …
y=- x … -3 -2 -1 0 1 2 3 …
y … …
a越大,开口越大
因为开口向下,a为负数,所以|a|越大,开口越小
课堂练习
填空:
(1)抛物线y=-9x2的顶点坐标是___________; 对称轴是________;
在_____________ 侧,y随着x的增大而增大;
在______________侧,y随着x的增大而减小;
当x=_______时,函数y的值最大,最大值是________;
抛物线y=-9x2在x轴的________方(除顶点外).
(0,0)
y轴
对称轴的左
对称轴的右
0
0
下
