华师大版数学九年级下册26.2.3二次函数y=ax^2+bx+c的图象与性质 课件(共25张PPT)
文档属性
| 名称 | 华师大版数学九年级下册26.2.3二次函数y=ax^2+bx+c的图象与性质 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 09:45:36 | ||
图片预览






文档简介
(共25张PPT)
二次函数y=+bx+c的图象与性质
华师大·九下
数学的真谛就在于不断寻求用越来越简单的方法证明定理和解决数学问题. ——加德纳
26.2.3
亲爱的同学们,上两节课我们学习了y=ax2+c 和y=a(x-h)2 (a≠0)的图象和性质,请同学们回忆一下当a>0, a<0时函数的具体性质?
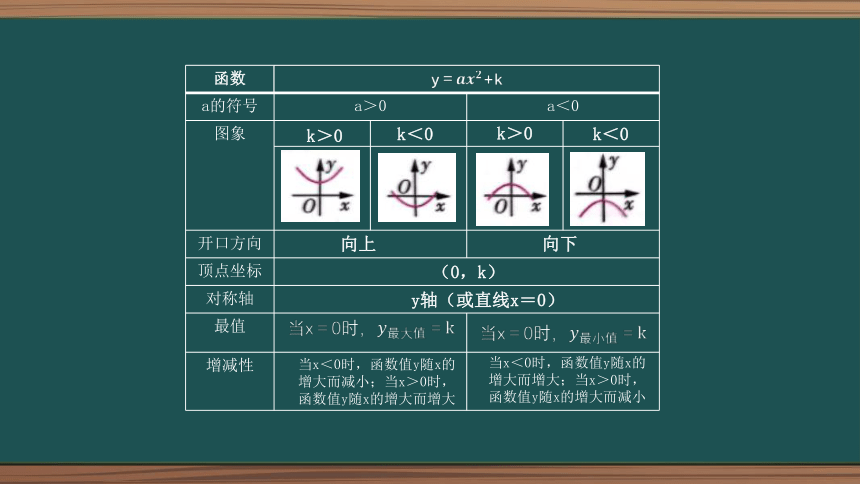
函数 y=+k a的符号 a>0 a<0 图象
开口方向 顶点坐标 对称轴 最值 增减性 k>0
k<0
k>0
k<0
向上
向下
(0,k)
y轴(或直线x=0)
当x=0时,=k
当x=0时,=k
当x<0时,函数值y随x的增大而减小;当x>0时,函数值y随x的增大而增大
当x<0时,函数值y随x的增大而增大;当x>0时,函数值y随x的增大而减小
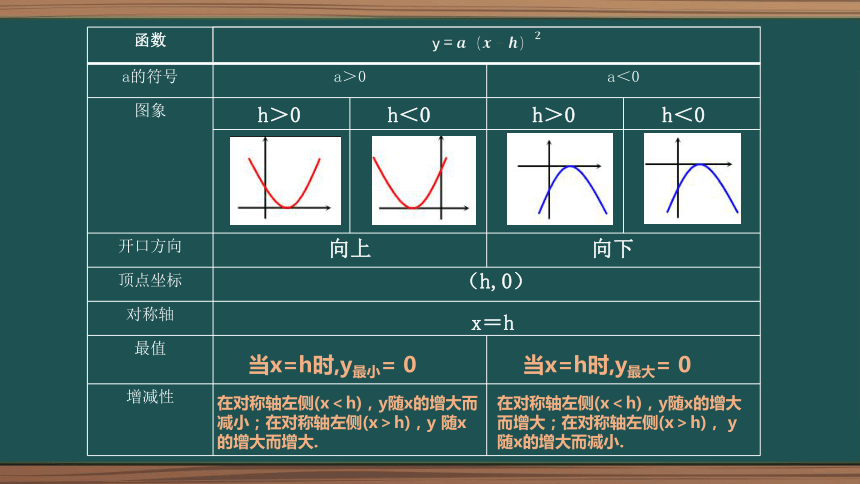
函数 y= a的符号 a>0 a<0 图象
开口方向 顶点坐标 对称轴 最值 增减性 h>0
h<0
h>0
h<0
向上
向下
(h,0)
x=h
当x=h时,y最小= 0
当x=h时,y最大= 0
在对称轴左侧(x<h),y随x的增大而减小;在对称轴左侧(x>h),y 随x的增大而增大.
在对称轴左侧(x<h),y随x的增大而增大;在对称轴左侧(x>h), y 随x的增大而减小.
我们学习了二次函数向上下或左右移动的情况,那同时包括这两个方向时的函数应该是什么样子的呢?
01.二次函数y=的图象与性质
02.二次函数y=+bx+c的图象与性质
知
识
点
01
二次函数y=的图象与性质
试研究二次函数 的图象
仿照前两节课的内容尝试着试试看
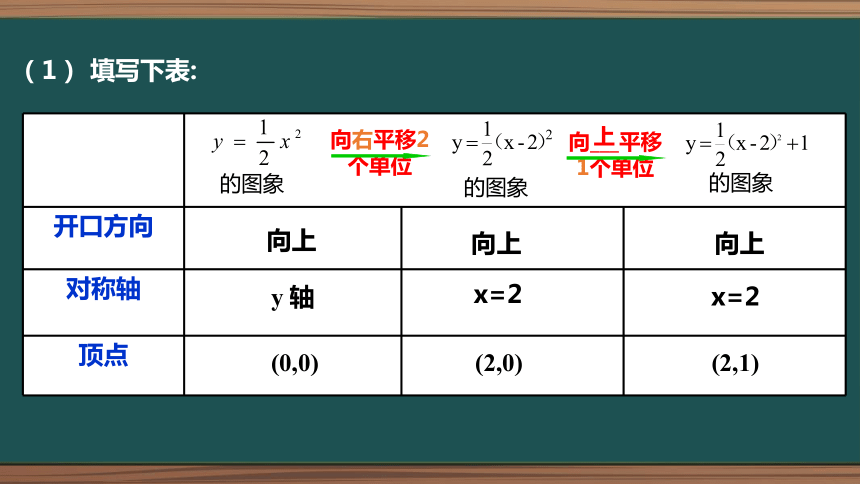
(1) 填写下表:
开口方向
对称轴
顶点
向右平移2个单位
向___平移1个单位
的图象
的图象
的图象
向上
向上
y 轴
(0,0)
x=2
x=2
向上
(2,0)
(2,1)
上
(2)从上表中 ,你能找到函数 的图象与函
数 的图象之间的关系吗
这两个函数的图象开口方向相同。但是对称轴和顶点坐标不同。
进一步 , 你能发现函数
有哪些性质?
据此,可以由函数 的性质,得到函数 的性质;
当 x_________时,函数值y随x的增大而减小;当 x_________时,函数值y随x的增大而增大;当 x_________时 , 函数取得最 _______值,最 ______值 y=______。
<2
>2
=2
小
小
1
y=a(x-h)2+k a>0 a<0
图象
开口
对称性 顶点
增减性
开口向上
开口向下
a的绝对值越大,开口越小
直线x=h
顶点是最低点(h,k)
顶点是最高点(h,k)
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
h>0 k>0
h<0 k>0
h<0 k<0
h>0 k<0
(h,0)
二次函数y=a(x-h)2+k的性质:
课堂练习
填空:
1. 说出下列二次函数的开口方向、对称轴及顶点坐标。
(1) y=2(x+3)2 -1
(2) y=-3(x-1)2 +2
(3) y=5(x+2)2 -6
(4) y=-(x-6)2 -8
(5) y=7(x-8)2 +5
向上, x=-3,(-3,-1)
向下, x=1,(1,2)
向上, x=-2,(-2,-6)
向下, x=6,(6,-8)
向上, x=8,(8,5)
2. 在抛物线y=(x+2)2-4上的一个点是( )
A.(4,4) B.(1,-4)
C.(-2,-4) D.(0,4)
C
02
02.二次函数y=+bx+c的图象与性质
例4:画出函数 的图象,并说明这个函数具有哪些性质。
这个二次函数不在我们学过的五个函数里面?那我们要怎么办呢?想一想
以前的一元二次方程,能不能利用配方法将这个函数转化成我们学过的二次函数呢?
例4:画出函数 的图象,并说明这个函数具有哪些性质。
例4:画出函数 的图象,并说明这个函数具有哪些性质。
这个函数的图象开口向下,
对称轴为直线x=1,
顶点坐标为(1,-2)
当x=1时,=-2
当x<1时,y随x的增大而增大
当x>1时,y随x的增大而减小
试按照上面的方法,画出函数 的图象 由图象你能发现这个函数具有哪些性质
试按照上面的方法,整理函数
配方得
开口由a决定
(a>0,开口向上;a<0,开口向下)
顶点坐标( )
对称轴x
当x 时,
a>0时,
当x 时,y随x的增大而减小;
当x 时,y随x的增大而增大;
配方得
开口由a决定
(a>0,开口向上;a<0,开口向下)
顶点坐标( )
对称轴x
当x 时,
a<0时,
当x 时,y随x的增大而增大;
当x 时,y随x的增大而减小;
二次函数y=ax2+bx+c(a≠0)的图象和性质
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
课堂练习
填空:
1. 已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
D
课堂练习
2. 二次函数 的图象如图,反比例函数 与正比例函数 在同一坐标系内的大致图象是( )
D
二次函数y=+bx+c的图象与性质
华师大·九下
数学的真谛就在于不断寻求用越来越简单的方法证明定理和解决数学问题. ——加德纳
26.2.3
亲爱的同学们,上两节课我们学习了y=ax2+c 和y=a(x-h)2 (a≠0)的图象和性质,请同学们回忆一下当a>0, a<0时函数的具体性质?
函数 y=+k a的符号 a>0 a<0 图象
开口方向 顶点坐标 对称轴 最值 增减性 k>0
k<0
k>0
k<0
向上
向下
(0,k)
y轴(或直线x=0)
当x=0时,=k
当x=0时,=k
当x<0时,函数值y随x的增大而减小;当x>0时,函数值y随x的增大而增大
当x<0时,函数值y随x的增大而增大;当x>0时,函数值y随x的增大而减小
函数 y= a的符号 a>0 a<0 图象
开口方向 顶点坐标 对称轴 最值 增减性 h>0
h<0
h>0
h<0
向上
向下
(h,0)
x=h
当x=h时,y最小= 0
当x=h时,y最大= 0
在对称轴左侧(x<h),y随x的增大而减小;在对称轴左侧(x>h),y 随x的增大而增大.
在对称轴左侧(x<h),y随x的增大而增大;在对称轴左侧(x>h), y 随x的增大而减小.
我们学习了二次函数向上下或左右移动的情况,那同时包括这两个方向时的函数应该是什么样子的呢?
01.二次函数y=的图象与性质
02.二次函数y=+bx+c的图象与性质
知
识
点
01
二次函数y=的图象与性质
试研究二次函数 的图象
仿照前两节课的内容尝试着试试看
(1) 填写下表:
开口方向
对称轴
顶点
向右平移2个单位
向___平移1个单位
的图象
的图象
的图象
向上
向上
y 轴
(0,0)
x=2
x=2
向上
(2,0)
(2,1)
上
(2)从上表中 ,你能找到函数 的图象与函
数 的图象之间的关系吗
这两个函数的图象开口方向相同。但是对称轴和顶点坐标不同。
进一步 , 你能发现函数
有哪些性质?
据此,可以由函数 的性质,得到函数 的性质;
当 x_________时,函数值y随x的增大而减小;当 x_________时,函数值y随x的增大而增大;当 x_________时 , 函数取得最 _______值,最 ______值 y=______。
<2
>2
=2
小
小
1
y=a(x-h)2+k a>0 a<0
图象
开口
对称性 顶点
增减性
开口向上
开口向下
a的绝对值越大,开口越小
直线x=h
顶点是最低点(h,k)
顶点是最高点(h,k)
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
h>0 k>0
h<0 k>0
h<0 k<0
h>0 k<0
(h,0)
二次函数y=a(x-h)2+k的性质:
课堂练习
填空:
1. 说出下列二次函数的开口方向、对称轴及顶点坐标。
(1) y=2(x+3)2 -1
(2) y=-3(x-1)2 +2
(3) y=5(x+2)2 -6
(4) y=-(x-6)2 -8
(5) y=7(x-8)2 +5
向上, x=-3,(-3,-1)
向下, x=1,(1,2)
向上, x=-2,(-2,-6)
向下, x=6,(6,-8)
向上, x=8,(8,5)
2. 在抛物线y=(x+2)2-4上的一个点是( )
A.(4,4) B.(1,-4)
C.(-2,-4) D.(0,4)
C
02
02.二次函数y=+bx+c的图象与性质
例4:画出函数 的图象,并说明这个函数具有哪些性质。
这个二次函数不在我们学过的五个函数里面?那我们要怎么办呢?想一想
以前的一元二次方程,能不能利用配方法将这个函数转化成我们学过的二次函数呢?
例4:画出函数 的图象,并说明这个函数具有哪些性质。
例4:画出函数 的图象,并说明这个函数具有哪些性质。
这个函数的图象开口向下,
对称轴为直线x=1,
顶点坐标为(1,-2)
当x=1时,=-2
当x<1时,y随x的增大而增大
当x>1时,y随x的增大而减小
试按照上面的方法,画出函数 的图象 由图象你能发现这个函数具有哪些性质
试按照上面的方法,整理函数
配方得
开口由a决定
(a>0,开口向上;a<0,开口向下)
顶点坐标( )
对称轴x
当x 时,
a>0时,
当x 时,y随x的增大而减小;
当x 时,y随x的增大而增大;
配方得
开口由a决定
(a>0,开口向上;a<0,开口向下)
顶点坐标( )
对称轴x
当x 时,
a<0时,
当x 时,y随x的增大而增大;
当x 时,y随x的增大而减小;
二次函数y=ax2+bx+c(a≠0)的图象和性质
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
课堂练习
填空:
1. 已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A.b≥-1 B.b≤-1 C.b≥1 D.b≤1
D
课堂练习
2. 二次函数 的图象如图,反比例函数 与正比例函数 在同一坐标系内的大致图象是( )
D
