第6章角与直线相交复习课件

课件16张PPT。
角与直线相交复习岭头中学 王万贵
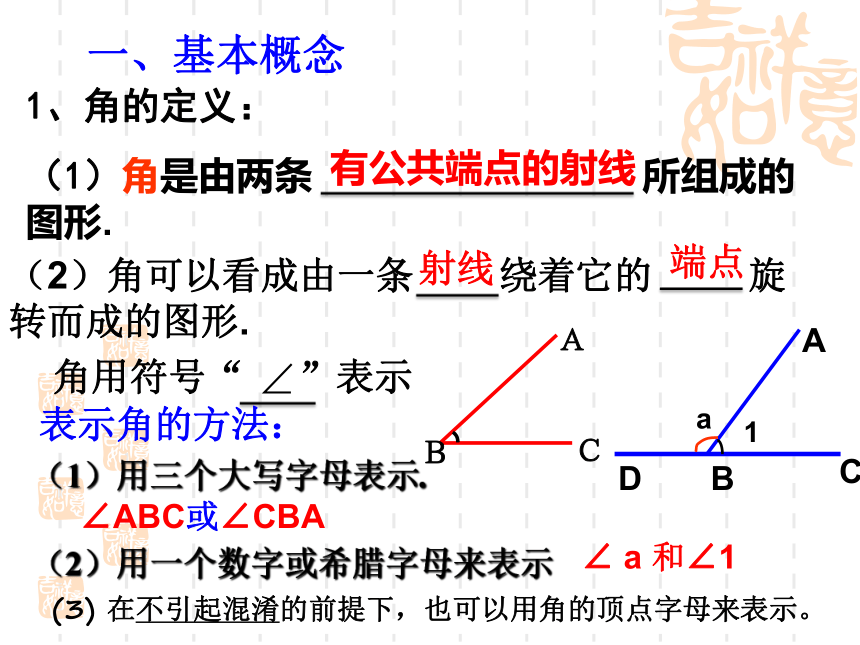
2015.11、角的定义：
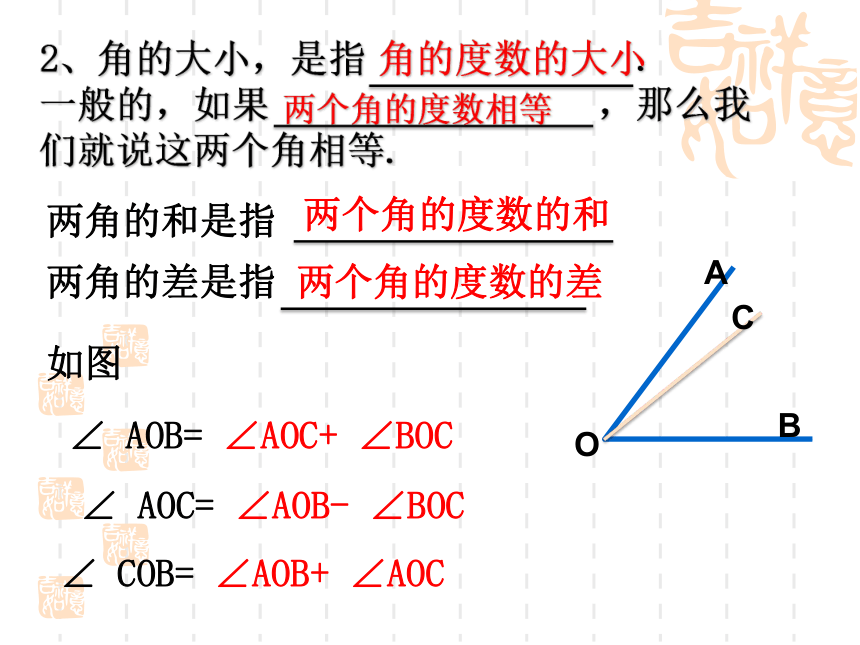
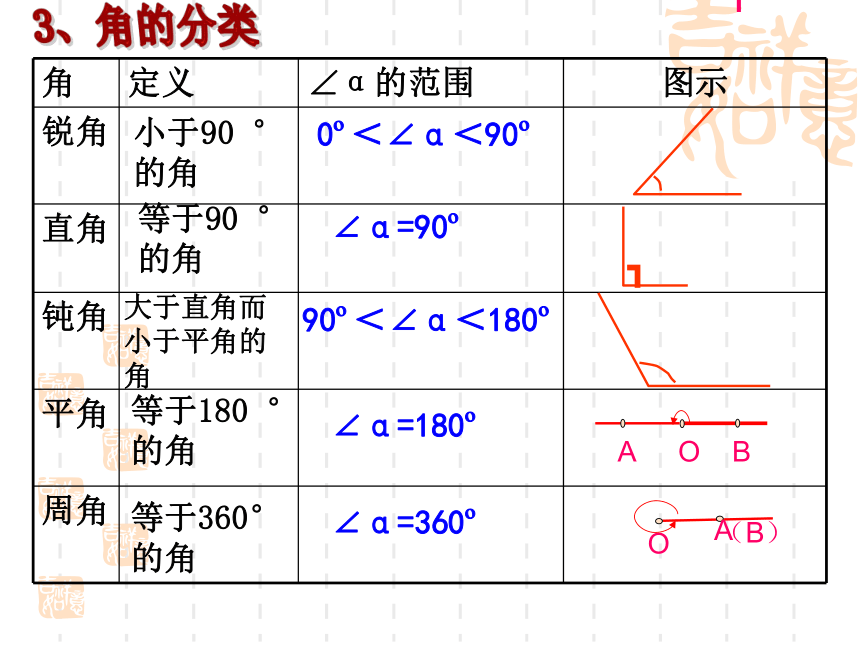
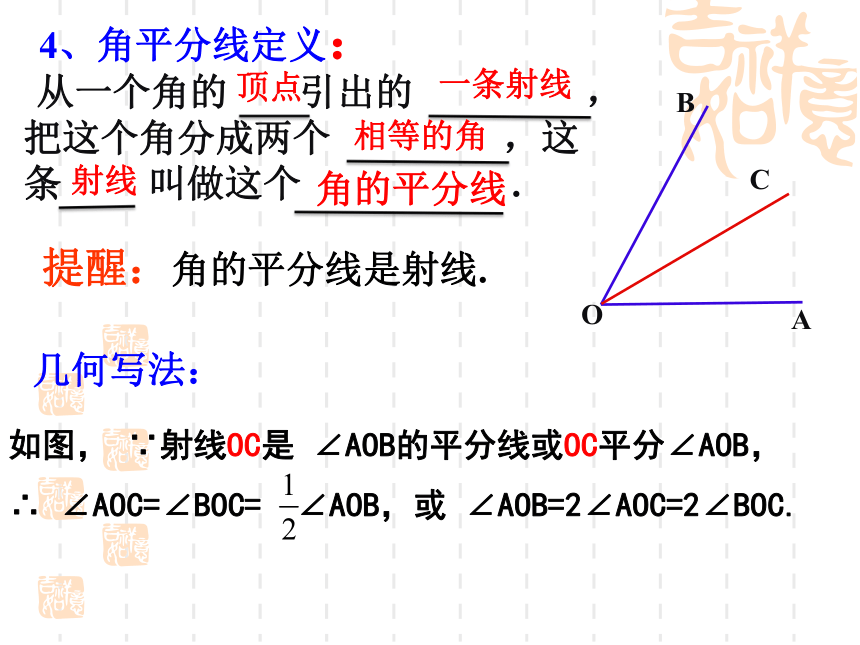
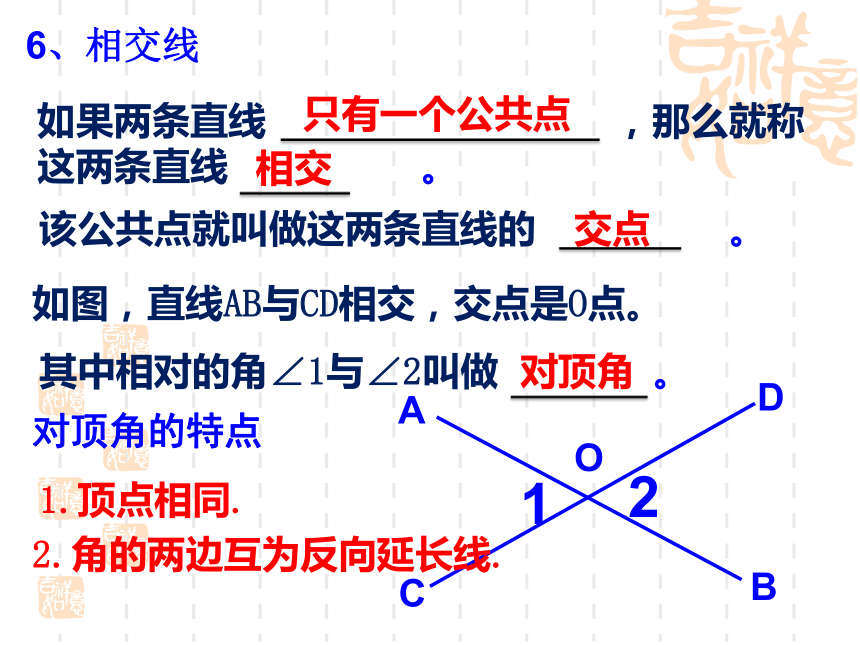
（1）角是由两条 所组成的图形.一、基本概念有公共端点的射线（2）角可以看成由一条 绕着它的 旋转而成的图形. 射线端点角用符号“ ”表示表示角的方法：（1）用三个大写字母表示.∠ABC或∠CBAa1（2）用一个数字或希腊字母来表示∠ a 和∠1(3) 在不引起混淆的前提下，也可以用角的顶点字母来表示。2、角的大小，是指 .一般的，如果 ，那么我们就说这两个角相等.角的度数的大小两个角的度数相等两角的和是指两个角的度数的和两角的差是指两个角的度数的差如图 ∠ AOB= ∠AOC+ ∠BOC∠ COB= ∠AOB+ ∠AOC∠ AOC= ∠AOB- ∠BOC3、角的分类小于90 °的角0o＜∠α＜90o等于90 °的角∠α=90o大于直角而小于平角的角等于180 °的角90o＜∠α＜180o∠α=180o等于360°的角∠α=360o┐OABC4、角平分线定义：如图， ∵射线OC是 ∠AOB的平分线或OC平分∠AOB， ∴ ∠AOC=∠BOC= ∠AOB，或 ∠AOB=2∠AOC=2∠BOC.几何写法：提醒：角的平分线是射线.顶点 从一个角的 引出的 ，把这个角分成两个 ，这条 叫做这个 .一条射线相等的角射线角的平分线5、互余与互补如果两个角的和是直角,那么这两个角互为余角∠1 + ∠2 = 90 ° ∠1 与 ∠2互余 如果两个角的和是平角,那么这两个角互为补角。∠3+ ∠4 = 180 ° ∠3与∠4 互补如果两条直线 ，那么就称这两条直线 。该公共点就叫做这两条直线的 。只有一个公共点相交交点6、相交线如图，直线AB与CD相交，交点是O点。其中相对的角∠1与∠2叫做 。对顶角对顶角的特点1.顶点相同.2.角的两边互为反向延长线.如果两条直线相交 ，那么这两条直线互相垂直。O图中，直线AB与直线CD垂直记作：AB⊥CD；直线 m 与直线 n 垂直记作：m⊥n ；互相垂直的两条直线的交点叫做垂足。是图形中“垂直”(直角)的标记。7、两条直线垂直的概念其中一条直线叫做另一条直线的垂线；有一个直角1、∵AB⊥CD（已知）
∴∠1=90 °（垂直的定义）2、∵∠1=90°（已知）
∴AB⊥CD（垂直的定义） 从直线外一点到这条直线的垂线段的长度，叫做点到直线的距离。8、点到直线的距离二、基本性质同角或等角的余角相等；同角或等角的补角相等1、互余与互补的性质2、对顶角性质对顶角相等3、垂线的性质 （1）在同一平面内，过一点有且仅有一条直线垂直于已知直线。 （2）直线外一点与直线上各点连结的所有线段中，垂线段最短。三、基本技能1、角的度量、角度制 1o =60'
1 ′ =( ) o
1 ' =60 "
1 " =( ) '
2、角的大小比较方法（1）度量法（2）叠合法3、角的和与差的画法及计算4、相交线、垂线的画法及有关计算例题解析（1）若OC ⊥OA，OB ⊥OD，则图中共有 个直角，有 个锐角，有 个钝角.
若∠1＝58°24′16″
则∠AOD= ∠2= （2）若OC、OB把∠AOD三等分，OP平分∠AOD，且∠COP=25 °，求∠AOD的度数. 如图，OC、OB是∠AOD内两条射线，则图中共有 个角，分别表示为图中相等的角是P（3）若OA、OD的反向延长线OE、OF，OC ⊥OA，∠3=31.8 ° ，则∠AOF= °， ∠ EOF= °. F练一练1、（1）将37.56°化为度分秒；2、已知一个角的补角是这个角的余角的3倍，求这个角的度数。（2）将123°32′42″化为度.归纳小结1.今天你收获了哪些知识？2.你掌握了哪些方法？ 布置作业:
1、作业本（2）A组
2、课文P176—177目标与评定T7—16再见！