2.2 二次函数的图像(1)
图片预览






文档简介
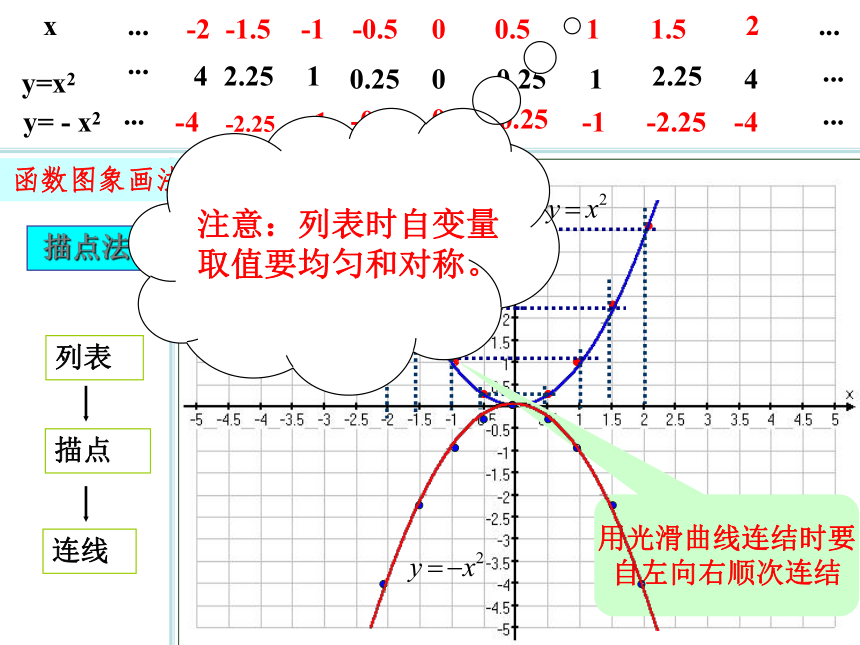
课件25张PPT。2.2 二次函数的图像(1)回顾旧知一、正比例函数y=kx(k ≠ 0)其图象是什么。二、一次函数y=kx+b(k ≠ 0)其图象又是什么。正比例函数y=kx(k ≠ 0)其图象是一条经过原点的直线。一次函数y=kx+b(k ≠ 0)其图象也是一条直线。三、反比例函数 (k ≠ 0)其图象又是什么。反比例函数 (k ≠ 0)其图象是双曲线。 二次函数y=ax2+bx+c(a ≠ 0)其图象又是什么呢?二次函数y=ax2的图像 函数图象画法列表描点连线00.2512.2540.2512.254 描点法用光滑曲线连结时要
自左向右顺次连结0-0.25-1-2.25-4-0.25-1-2.25-4注意:列表时自变量
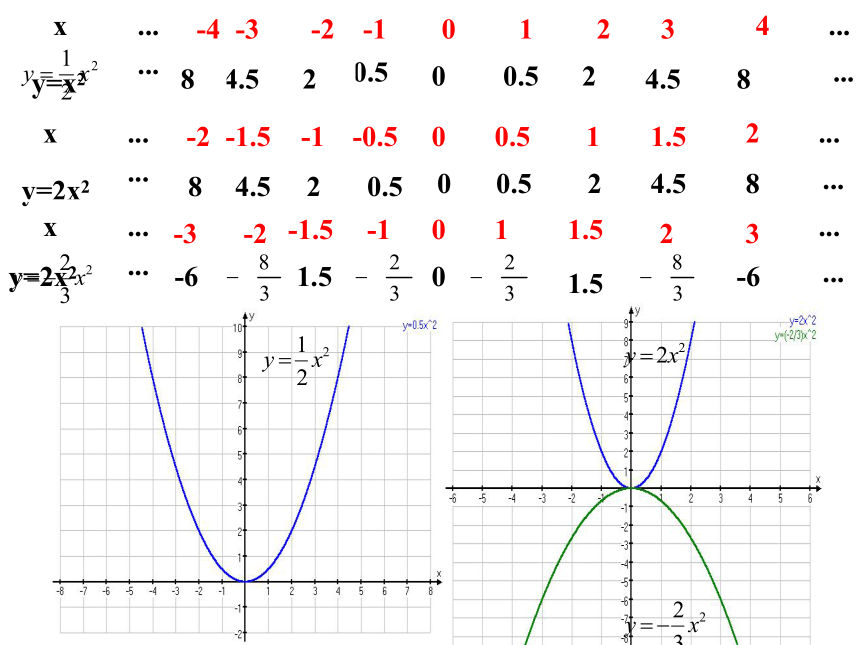
取值要均匀和对称。00.524.580.524.5800.524.580.524.5801.5-61.5-6二次函数y=ax2的图象形如物体抛射时
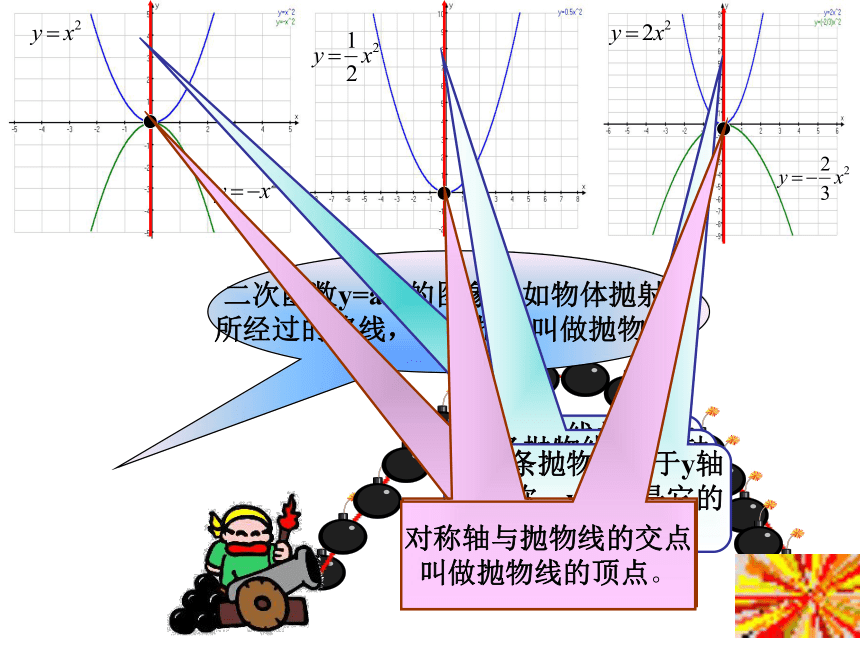
所经过的路线,我们把它叫做抛物线。这条抛物线关于y轴
对称,y轴就是它的
对称轴。 这条抛物线关于y轴
对称,y轴就是它的
对称轴。 这条抛物线关于y轴
对称,y轴就是它的
对称轴。 对称轴与抛物线的交点
叫做抛物线的顶点。对称轴与抛物线的交点
叫做抛物线的顶点。对称轴与抛物线的交点
叫做抛物线的顶点。欣赏生活中的抛物线焰火合作探究二次函数y=-x2的图象是什么形状?
它与二次函数y=x2的图象有什么关系?yxxy=x2y=-x2yOO相同点:顶点都是原点(0,0);对称轴都是y轴.开口大小一样 不同点:最值不同;一个有最高点,一个有最低点.开口方向不同;函数值随自变量增大的变化趋势不同;它们的图象关于x轴对称.联系:图象都是抛物线;(0,0)(0,0)y轴y轴在x轴的上方(除顶点外)在x轴的下方(除顶点外)向上向下当x=0时,最小值为0。当x=0时,最大值为0。二次函数y=ax2的性质1、顶点坐标与对称轴2、位置与开口方向3、增减性与极值2、练习2
在同一坐标系内,抛物线y=x2与抛物线
y= -x2的位置有什么关系? 如果在同一坐标系内
画函数y=ax2与y= -ax2的图象,怎样画才简便?
答:抛物线抛物线y=x2与抛物线 y= -x2 既关于x轴对称,
又关于原点对称。只要画出y=ax2与y= -ax2中的一条抛物线,
另一条可利用关于x轴对称或关于原点对称来画。增减性 二次函数y=x2,当x<0时
(在对 称轴的左侧),y随
着x的增大而减小. 二次函数y=x2,当x>0时
(在对称轴的右侧),y随
着x的增大而增大.
二次函数y=-x2,当x<0时
(在对称轴的左侧),y随
着x的增大而增大.
二次函数y=-x2,当x>0时
(在对称轴的右侧),y随
着x的增大而减小. 02.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.1.抛物线y=ax2的顶点是原点,对称轴是y轴.由二次函数y=x2和y=-x2知:(0,0)y轴对称轴右对称轴左00上><不能(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧(即x 0时),y随着x的增大而增大;在 侧(即x 0时),y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 . 在抛物线y=2x2的图象上能找到纵坐标为负数的点吗? .这是因为抛物线y=2x2在x轴的
方(除顶点外).(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.下增大而增大增大而减小0≠例1、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。解(1)把(-2,-8)代入y=ax2,得
-8=a(-2)2,解出a= -2,
所求函数解析式为 y= -2x2.(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上。(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,
它们分别是y=-2x2若抛物线y=ax2 (a ≠ 0),过点(-1,3)。
(1)则a的值是 ;
(2)对称轴是 ,开口 。
(3)顶点坐标是 ,顶点是抛物线上
的 。抛物线在x轴的 方(除顶
点外)。填一填3y轴向上(0,0)最低点上谈收获:1.二次函数y=ax2(a≠0)的图像是一条抛物线.2.图象关于y轴对称,顶点是坐标原点.3.当a>0时,抛物线的开口向上,顶点是抛物线上的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点.提高拓展0
自左向右顺次连结0-0.25-1-2.25-4-0.25-1-2.25-4注意:列表时自变量
取值要均匀和对称。00.524.580.524.5800.524.580.524.5801.5-61.5-6二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。这条抛物线关于y轴
对称,y轴就是它的
对称轴。 这条抛物线关于y轴
对称,y轴就是它的
对称轴。 这条抛物线关于y轴
对称,y轴就是它的
对称轴。 对称轴与抛物线的交点
叫做抛物线的顶点。对称轴与抛物线的交点
叫做抛物线的顶点。对称轴与抛物线的交点
叫做抛物线的顶点。欣赏生活中的抛物线焰火合作探究二次函数y=-x2的图象是什么形状?
它与二次函数y=x2的图象有什么关系?yxxy=x2y=-x2yOO相同点:顶点都是原点(0,0);对称轴都是y轴.开口大小一样 不同点:最值不同;一个有最高点,一个有最低点.开口方向不同;函数值随自变量增大的变化趋势不同;它们的图象关于x轴对称.联系:图象都是抛物线;(0,0)(0,0)y轴y轴在x轴的上方(除顶点外)在x轴的下方(除顶点外)向上向下当x=0时,最小值为0。当x=0时,最大值为0。二次函数y=ax2的性质1、顶点坐标与对称轴2、位置与开口方向3、增减性与极值2、练习2
在同一坐标系内,抛物线y=x2与抛物线
y= -x2的位置有什么关系? 如果在同一坐标系内
画函数y=ax2与y= -ax2的图象,怎样画才简便?
答:抛物线抛物线y=x2与抛物线 y= -x2 既关于x轴对称,
又关于原点对称。只要画出y=ax2与y= -ax2中的一条抛物线,
另一条可利用关于x轴对称或关于原点对称来画。增减性 二次函数y=x2,当x<0时
(在对 称轴的左侧),y随
着x的增大而减小. 二次函数y=x2,当x>0时
(在对称轴的右侧),y随
着x的增大而增大.
二次函数y=-x2,当x<0时
(在对称轴的左侧),y随
着x的增大而增大.
二次函数y=-x2,当x>0时
(在对称轴的右侧),y随
着x的增大而减小. 02.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.1.抛物线y=ax2的顶点是原点,对称轴是y轴.由二次函数y=x2和y=-x2知:(0,0)y轴对称轴右对称轴左00上><不能(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧(即x 0时),y随着x的增大而增大;在 侧(即x 0时),y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 . 在抛物线y=2x2的图象上能找到纵坐标为负数的点吗? .这是因为抛物线y=2x2在x轴的
方(除顶点外).(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.下增大而增大增大而减小0≠例1、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。解(1)把(-2,-8)代入y=ax2,得
-8=a(-2)2,解出a= -2,
所求函数解析式为 y= -2x2.(2)因为 ,所以点B(-1 ,-4)
不在此抛物线上。(3)由-6=-2x2 ,得x2=3,
所以纵坐标为-6的点有两个,
它们分别是y=-2x2若抛物线y=ax2 (a ≠ 0),过点(-1,3)。
(1)则a的值是 ;
(2)对称轴是 ,开口 。
(3)顶点坐标是 ,顶点是抛物线上
的 。抛物线在x轴的 方(除顶
点外)。填一填3y轴向上(0,0)最低点上谈收获:1.二次函数y=ax2(a≠0)的图像是一条抛物线.2.图象关于y轴对称,顶点是坐标原点.3.当a>0时,抛物线的开口向上,顶点是抛物线上的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点.提高拓展0
同课章节目录
