第3章 圆的基本性质单元达标测试卷(含解析)2023-2024学年浙教版九年级数学上册
文档属性
| 名称 | 第3章 圆的基本性质单元达标测试卷(含解析)2023-2024学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 494.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-04 14:40:09 | ||
图片预览


文档简介
浙教版九年级数学上册第3章圆的基本性质单元达标测试卷
一、单选题
1.如图,图中的弦共有( )
A.1条 B.2条 C.3条 D.4条
2.平面直角坐标系中,O为坐标原点,点A的坐标为( ,1),将OA绕原点O按逆时针方向旋转90°得OB,则点B的坐标为( )
A.(1, ) B.(-1, ) C.(- ,1) D.( ,-1)
3.如图,⊙O的直径为10,AB为弦,OC⊥AB,垂足为C,若OC=3,则弦AB的长为( )
A.8 B.6 C.4 D.10
4.在联欢会上,甲、乙、丙3人分别站在不在同一直线上的三点A、B、C上,他们在玩抢凳子的游戏,要在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放的最恰当的位置是△ABC的( )
A.三条高的交点 B.重心
C.内心 D.外心
5.如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是( )
A.30° B.40° C.50° D.60°
6.半径为 的圆的内接正六边形的边心距是( )
A. B. C. D.
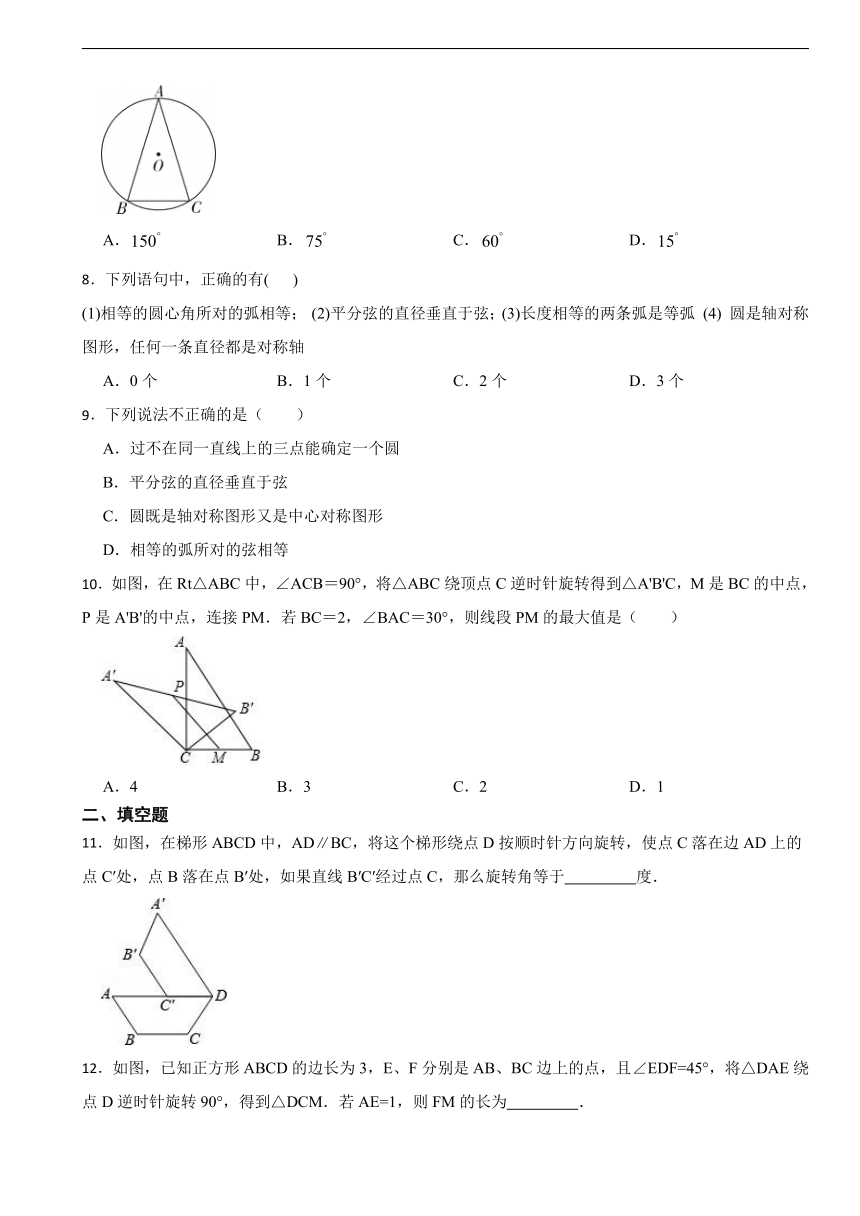
7.如图所示,在中,,则的度数为( ).
A. B. C. D.
8.下列语句中,正确的有( )
(1)相等的圆心角所对的弧相等; (2)平分弦的直径垂直于弦;(3)长度相等的两条弧是等弧 (4) 圆是轴对称图形,任何一条直径都是对称轴
A.0个 B.1个 C.2个 D.3个
9.下列说法不正确的是( )
A.过不在同一直线上的三点能确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.相等的弧所对的弦相等
10.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
A.4 B.3 C.2 D.1
二、填空题
11.如图,在梯形ABCD中,AD∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于 度.
12.如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .
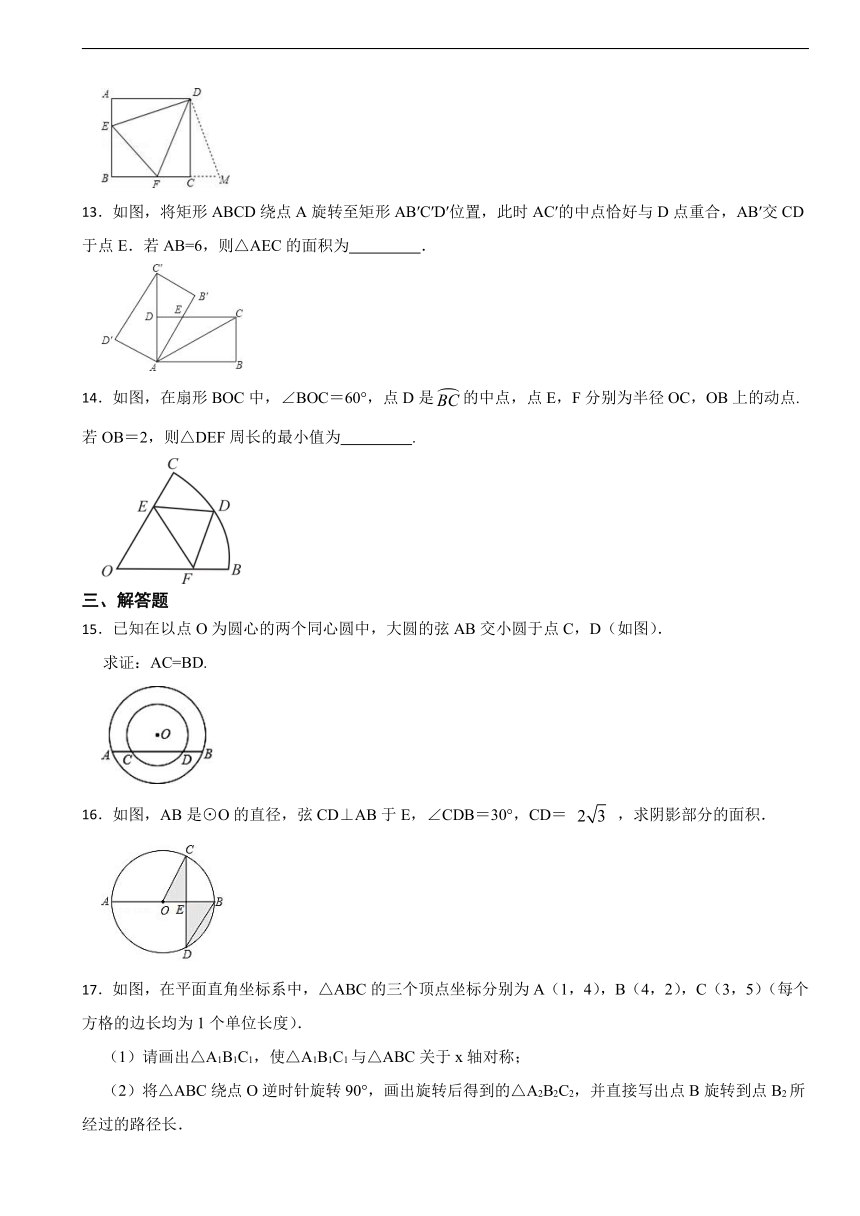
13.如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为 .
14.如图,在扇形BOC中,∠BOC=60°,点D是的中点,点E,F分别为半径OC,OB上的动点.若OB=2,则△DEF周长的最小值为 .
三、解答题
15.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
16.如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
17.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
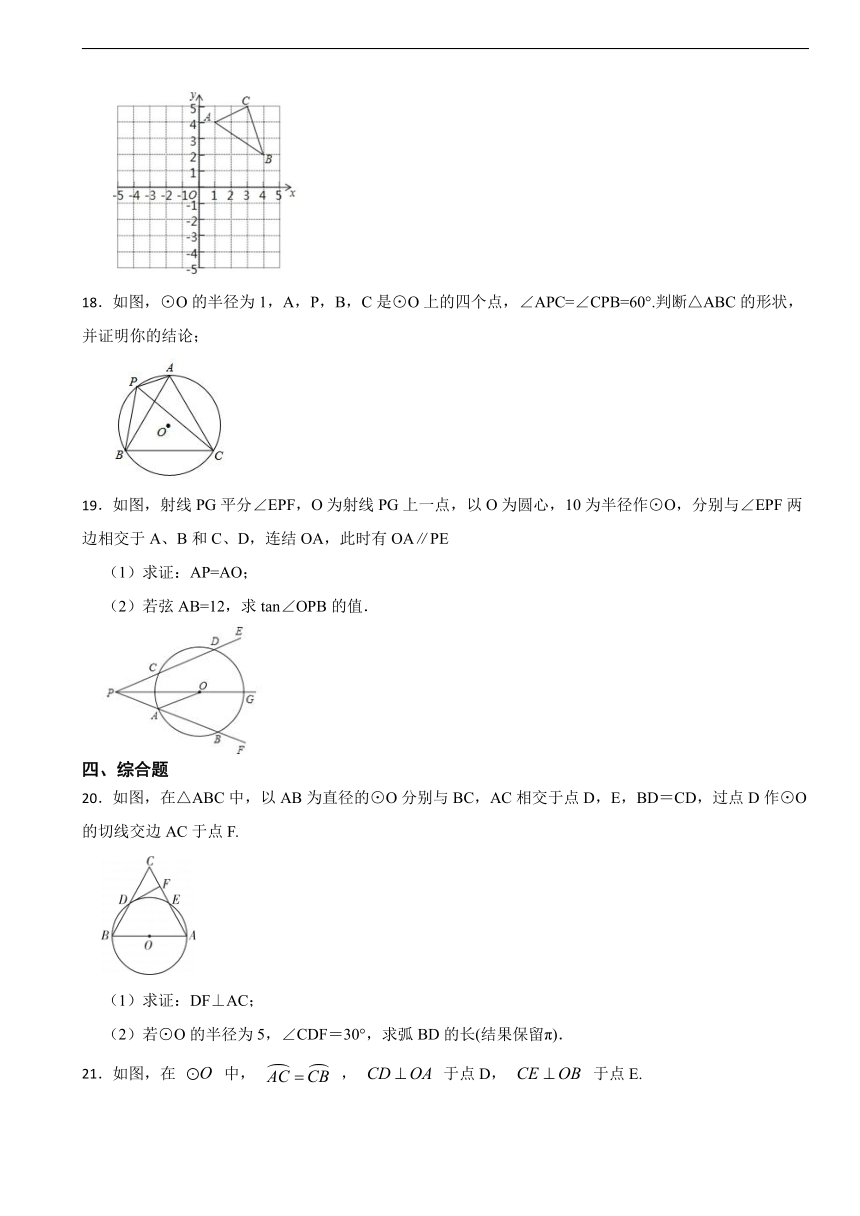
18.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.判断△ABC的形状,并证明你的结论;
19.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE
(1)求证:AP=AO;
(2)若弦AB=12,求tan∠OPB的值.
四、综合题
20.如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求弧BD的长(结果保留π).
21.如图,在 中, , 于点D, 于点E.
(1)求证: ;
(2)若 ,求四边形 的面积.
22.如图,将矩形绕点B旋转得到矩形,点E在上,延长交于点H.
(1)求证:;
(2)连接,若,求的度数.
23.如图1,⊙O的直径AB为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧 向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
(1)求证:△ABC∽△PDC
(2)如图2,当点P到达B点时,求CD的长;
(3)设CD的长为 .在点P的运动过程中, 的取值范围为(请直接写出案).
答案解析部分
1.【答案】B
【解析】【解答】解:图形中有弦AB和弦CD,共2条,
故答案为:B.
【分析】由连接圆上任意两点间的距离就是弦即可判断得出答案.
2.【答案】B
【解析】【解答】过点B作BC⊥x轴于点C,过点B作BC⊥y轴于点F,
∵点A的坐标为( ,1),将OA绕原点O逆时针旋转90°到OB的位置,
∴BC ,CO=1,
∴点B的坐标为:(﹣1, ).
故答案为:B.
【分析】先根据旋转的性质作图,利用图象则可求得点B的坐标.
3.【答案】A
【解析】【解答】解:连接OA,
∵OA=5,OC=3,OC⊥AB,
∴AC= =4,
∵OC⊥AB,
∴AB=2AC=2×4=8.
故答案为:A.
【分析】连接OA,利用勾股定理求出AC的长,根据垂径定理可得AB=2AC,从而求出AB的长.
4.【答案】D
【解析】【解答】解:∵三角形的三条垂直平分线的交点到中间的凳子的距离相等,
∴凳子应放在△ABC的三条垂直平分线的交点最适当.
故答案为:D.
【分析】为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
5.【答案】C
【解析】【解答】解:∵∠AOB与∠ACB都对 ,且∠AOB=100°,
∴∠ACB= ∠AOB=50°,
故选C
【分析】根据图形,利用圆周角定理求出所求角度数即可.
6.【答案】C
【解析】【解答】解:如图,连接OA、OB,过点O作OH垂直AB于点H,OH即为正六边形边心距.
∵六边形ABCDEF为正六边形
∴ ,OA=OB=AB=a,AH=BH= ,
∴
即半径为 的圆的内接正六边形的边心距是.
故答案为:C.
【分析】连接OA、OB,过点O作OH垂直AB于点H,OH即为正六边形边心距,根据正六边形的性质用勾股定理可求解.
7.【答案】B
【解析】【解答】解:∵,
∴AB=AC,
∴∠B=∠C=(180°-∠A)=(180°-30°)=75°.
故答案为B:.
【分析】利用同圆和等圆中,相等的弧所对的弦相等,可证得AB=AC,利用等边对等角及三角形的内角和定理可求出∠B的度数.
8.【答案】A
【解析】【解答】(1)、不符合题意,需要添加前提条件,即在同圆或等圆中;(2)、不符合题意,平分的弦不能是直径;(3)、不符合题意,等弧是指长度和度数都相等的弧;(4)、不符合题意,圆的对称轴是直径所在的直线.
故答案为:A.
【分析】在同圆或等圆中,相等的圆心角所对的弧相等,据此判断(1);平分弦(不是直径)的直径垂直于弦,据此判断(2);能重合的弧叫做等弧,据此判断(3);圆是轴对称图形,任何一条直径所在的直线都是对称轴,据此判断(4).
9.【答案】B
【解析】【解答】解:A、过不在同一直线上的三点能确定一个圆,正确,不符合题意;
B、平分弦(不是直径)的直径垂直于弦,故原命题错误,符合题意;
C、圆既是轴对称图形又是中心对称图形,正确,不符合题意;
D、相等的弧所对的弦相等,正确,不符合题意.
故答案为:B.
【分析】根据确定圆的条件可判断A;根据垂径定理可判断B;根据轴对称图形、中心对称图形的概念可判断C;根据弧、弦的关系可判断D.
10.【答案】B
【解析】【解答】解:如图连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4,
根据旋转不变性可知,A′B′=AB=4,
∴A′P=PB′,
∴PC= A′B′=2,
∵CM=BM=1,
又∵PM≤PC+CM,即PM≤3,
∴PM的最大值为3(此时P、C、M共线).
故答案为:B.
【分析】连接PC,根据∠A=30°,BC=2,可知AB的值,根据旋转的性质可知A′B′=AB,进而可知A′P、PB′、PC的知,结合图形和三角形三边关系即可得出PM的取值范围,进而可知P、C、M共线时,PM值最大,即可选出答案.
11.【答案】60
【解析】【解答】解:连接CC′,如图所示:
则B′、C′、C在一条直线上,
由旋转的性质得:∠1=∠2,DC′=DC,
∴∠3=∠4,
∵A′D′∥B′C′,
∴∠2=∠3,
∴∠1=∠3=∠4,
∴△CDC′是等边三角形,
∴∠CDC′=60°;
故答案为:60.
【分析】根据旋转的性质“对应点与旋转中心连线所成的角度都等于旋转的角度”可求解。
12.【答案】2.5
【解析】【解答】∵△DAE逆时针旋转90°得到△DCM,∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,∴DE=DM,∠EDM=90°,∴∠EDF+∠FDM=90°,∵∠EDF=45°,∴∠FDM=∠EDF=45°,
在△DEF和△DMF中, ,∴△DEF≌△DMF(SAS),∴EF=MF,设EF=MF=x,
∵AE=CM=1,且BC=3,∴BM=BC+CM=3+1=4,∴BF=BM﹣MF=BM﹣EF=4﹣x,
∵EB=AB﹣AE=3﹣1=2,在Rt△EBF中,由勾股定理得EB2+BF2=EF2, 即22+(4﹣x)2=x2,
解得:x= , ∴FM= .
【分析】 根据旋转的性质得出F、C、M三点共线,DE=DM,∠EDM=90°,进而得出∠FDM=∠EDF=45°,然后利用SAS判断出△DEF≌△DMF,根据全等三角形的对应边相等得出EF=MF,设EF=MF=x,然后根据勾股定理建立方程,求解即可得出答案
13.【答案】
【解析】【解答】解:∵旋转后AC的中点恰好与D点重合,即AD= AC′= AC,
∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,
∴∠DAD′=60°,∴∠DAE=30°,
∴∠EAC=∠ACD=30°,∴AE=CE.
在Rt△ADE中,设AE=EC=x,
则有DE=DC﹣EC=AB﹣EC=6﹣x,AD= ×6=2 ,
根据勾股定理得:x2=(6﹣x)2+(2 )2,
解得:x=4,∴EC=4,
则S△AEC= EC AD=4 .
故答案为:4 .
【分析】根据旋转的性质及中点的定义得出AD= AC′= AC,根据含30°直角三角形的边之间的关系得出在Rt△ACD中,∠ACD=30°,故DAC=60°,进而得出∠DAD′=60°,∠DAE=30°,∠EAC=∠ACD=30°,根据等角对等边得出AE=CE.在Rt△ADE中,设AE=EC=x,则有DE=DC﹣EC=AB﹣EC=6﹣x,AD=,根据UGG多了建立方程,求解得出x的值,然后滚局三角形的面积计算方算出答案。
14.【答案】
【解析】【解答】解:连接OD,分别作D点关于OB、OC的对称点M、N,连接OM、ON,MN,MN交OB于F,交OC于E,交OD于P,如图,
∵ED=EN,FM=FD,
∴△DEF的周长=ED+EF+FD=EN+EF+FM=MN,
∴此时△DEF的周长最小,
∵点D是 的中点,
∴∠BOD=∠COD= ∠BOC=30°,
∵M点与D点关于OB对称,
∴∠MOB=∠BOD=30°,OM=OD=2,
同理得∠NOC=∠COD=30°,ON=OD=2,
∵∠MON=120°,OM=ON=2,
而∠MOP=60°,
∴OP⊥MN,∠OMN=∠ONM=30°,
∴PM=PN,
在Rt△OPM中,OP= OM=1,
∴PM= OP= ,
∴MN=2PM=2 ,
∴△DEF周长的最小值为2 .
故答案为:2 .
【分析】连接OD,分别作D点关于OB、OC的对称点M、N,连接OM、ON,MN,MN交OB于F,交OC于E,交OD于P,如图,由ED=EN,FM=FD,得△DEF周长=ED+EF+FD=EN+EF+FM=MN,根据两点之间线段最短可知此时△DEF的周长最小.求出∠MON=120°,OM=ON=2,继而求出EF即可.
15.【答案】解:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
【解析】【分析】过O作OE⊥AB于点E,根据垂径定理可知CE=DE、AE=BE,利用等式性质即可证明。
16.【答案】解:连接OD.
∵CD⊥AB,
∴CE=DE= CD= (垂径定理),
故S△OCE=S△ODE,
∴S阴=S扇形OBD,
又∵∠CDB=30°,
∴∠COB=60°(圆周角定理),
∴OC=2,
故S扇形OBD= = ,
即阴影部分的面积为 .
【解析】【分析】根据圆的轴对称性可将阴影部分的面积转化为扇形OBD的面积,因此计算出扇形OBD面积即为所求。
17.【答案】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
点B旋转到点B2所经过的路径长为:=π.
故点B旋转到点B2所经过的路径长是π.
【解析】【分析】(1)根据网格特点,找出点A、B、C关于x轴的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)分别找出点A、B、C绕点O逆时针旋转90°的对应点A2、B2、C2的位置,然后顺次连接即可,观察可知点B所经过的路线是半径为,圆心角是90°的扇形,然后根据弧长公式进行计算即可求解.
18.【答案】解:△ABC是等边三角形.
证明如下:在⊙O中,
∵∠BAC与∠CPB是弧BC所对的圆周角,∠ABC与∠APC是弧AC所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°=∠ACB,
∴△ABC为等边三角形.
【解析】【分析】利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
19.【答案】(1)证明:如图,
∵PG平分∠EPF,
∴∠CPO=∠APO.
∵AO∥PD,
∴∠CPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO.
(2)解:过点O作OH⊥AB于H,如图.
根据垂径定理可得AH=BH=AB=6,
∴PH=PA+AH=AO+AH=10+6=16.
在Rt△AHO中,
OH==8,
∴tan∠OPB==.
∴tan∠OPB的值为.
【解析】【分析】(1)由PG平分∠EPF可得∠CPO=∠APO,由AO∥PD可得∠CPO=∠AOP,从而有∠APO=∠AOP,则有AP=AO.
(2)过点O作OH⊥AB于H,如图2.根据垂径定理可得AH=BH=6,从而可求出PH,在Rt△AHO中,运用勾股定理可求出OH,然后运用锐角三角函数的定义就可解决问题.
20.【答案】(1)证明:连接OD,如图所示.
∵DF是⊙O的切线,D为切点,
∴OD⊥DF,
∴∠ODF=90°
∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠CFD=∠ODF=90°,
∴DF⊥AC.
(2)解:∵∠CDF=30°,
由(1)得∠ODF=90°,
∴∠ODB=180°-∠CDF-∠ODF=60°
∵OB=OD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴BD弧的长=
【解析】【分析】(1)连接OD,先证明OD是△ABC的中位线,可得OD∥AC,求出∠CFD=∠ODF=90°,即可得到DF⊥AC;
(2)先证明△OBD是等边三角形, 可得∠BOD=60°,再利用弧长公式求出答案即可。
21.【答案】(1)证明:连接 ,
∵ ,
∴ ,
∵ ,
∴ ;
(2)解:∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
同理可得 ,
∴ .
【解析】【分析】(1)利用等弧所对的圆心角相等,可证得∠AOC=∠BOC;再利用角平分线上的点到角两边的距离相等,可证得CD=CE.
(2)利用∠AOB的度数,可求出∠OC=60°,从而可求出∠OCD=30°;再利用30°角所对的直角边等于斜边的一半,可求出CD的长;然后利用勾股定理求出CD的长,利用三角形的面积公式,可求出△CDO的面积.
22.【答案】(1)证明:
∵四边形是矩形,
∴,,
由旋转性质,得:,,
∴,,
∵在矩形中,,
∴,
在和中,
,
∴,
(2)解:∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∵,
∴,即的度数为.
【解析】【分析】(1)由矩形的性质可得,, , 结合旋转的性质可得推出 ,,,利用平行线的性质可得,根据AAS证明;
(2)根据矩形的性质可得, 利用全等三角形的性质及等腰三角形的性质可得,再根据直角三角形两锐角互余即可求解.
23.【答案】(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠PCD,
又∵∠A=∠P,
∴△ABC∽△PDC
(2)解:∵∠ABC=30°,AB=4,
∴BC= ,
∵△ABC∽△PDC,
∴∠D=∠ABC=30°,
∴CD=6
(3)解:如图,
∵AB是直径,∠ABC=30°,AB=4
∴∠ACB=90°,∠A=∠P=60°,AC=2,
∵CD⊥PC,
∴∠PCD=90°,CD=PC tan60°,
∵PC的最小值=AC=2,PC的最大值为直径=4,
∴CD的最小值为2 ,最大值为4 ,
∴2 ≤CD≤4
【解析】【分析】(1)利用圆周角定理,进而用"两角法"证出相似;(2)利用30度角的正切,由AB求出BC,再求出CD;(3)可用PC及三角函数表示出CD,当PC最小时,CD最小,CD最大,PC最大.
一、单选题
1.如图,图中的弦共有( )
A.1条 B.2条 C.3条 D.4条
2.平面直角坐标系中,O为坐标原点,点A的坐标为( ,1),将OA绕原点O按逆时针方向旋转90°得OB,则点B的坐标为( )
A.(1, ) B.(-1, ) C.(- ,1) D.( ,-1)
3.如图,⊙O的直径为10,AB为弦,OC⊥AB,垂足为C,若OC=3,则弦AB的长为( )
A.8 B.6 C.4 D.10
4.在联欢会上,甲、乙、丙3人分别站在不在同一直线上的三点A、B、C上,他们在玩抢凳子的游戏,要在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放的最恰当的位置是△ABC的( )
A.三条高的交点 B.重心
C.内心 D.外心
5.如图,点A,B,C是⊙O上的三点,已知∠AOB=100°,那么∠ACB的度数是( )
A.30° B.40° C.50° D.60°
6.半径为 的圆的内接正六边形的边心距是( )
A. B. C. D.
7.如图所示,在中,,则的度数为( ).
A. B. C. D.
8.下列语句中,正确的有( )
(1)相等的圆心角所对的弧相等; (2)平分弦的直径垂直于弦;(3)长度相等的两条弧是等弧 (4) 圆是轴对称图形,任何一条直径都是对称轴
A.0个 B.1个 C.2个 D.3个
9.下列说法不正确的是( )
A.过不在同一直线上的三点能确定一个圆
B.平分弦的直径垂直于弦
C.圆既是轴对称图形又是中心对称图形
D.相等的弧所对的弦相等
10.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
A.4 B.3 C.2 D.1
二、填空题
11.如图,在梯形ABCD中,AD∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于 度.
12.如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .
13.如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为 .
14.如图,在扇形BOC中,∠BOC=60°,点D是的中点,点E,F分别为半径OC,OB上的动点.若OB=2,则△DEF周长的最小值为 .
三、解答题
15.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
16.如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
17.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
18.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.判断△ABC的形状,并证明你的结论;
19.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE
(1)求证:AP=AO;
(2)若弦AB=12,求tan∠OPB的值.
四、综合题
20.如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求弧BD的长(结果保留π).
21.如图,在 中, , 于点D, 于点E.
(1)求证: ;
(2)若 ,求四边形 的面积.
22.如图,将矩形绕点B旋转得到矩形,点E在上,延长交于点H.
(1)求证:;
(2)连接,若,求的度数.
23.如图1,⊙O的直径AB为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧 向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
(1)求证:△ABC∽△PDC
(2)如图2,当点P到达B点时,求CD的长;
(3)设CD的长为 .在点P的运动过程中, 的取值范围为(请直接写出案).
答案解析部分
1.【答案】B
【解析】【解答】解:图形中有弦AB和弦CD,共2条,
故答案为:B.
【分析】由连接圆上任意两点间的距离就是弦即可判断得出答案.
2.【答案】B
【解析】【解答】过点B作BC⊥x轴于点C,过点B作BC⊥y轴于点F,
∵点A的坐标为( ,1),将OA绕原点O逆时针旋转90°到OB的位置,
∴BC ,CO=1,
∴点B的坐标为:(﹣1, ).
故答案为:B.
【分析】先根据旋转的性质作图,利用图象则可求得点B的坐标.
3.【答案】A
【解析】【解答】解:连接OA,
∵OA=5,OC=3,OC⊥AB,
∴AC= =4,
∵OC⊥AB,
∴AB=2AC=2×4=8.
故答案为:A.
【分析】连接OA,利用勾股定理求出AC的长,根据垂径定理可得AB=2AC,从而求出AB的长.
4.【答案】D
【解析】【解答】解:∵三角形的三条垂直平分线的交点到中间的凳子的距离相等,
∴凳子应放在△ABC的三条垂直平分线的交点最适当.
故答案为:D.
【分析】为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
5.【答案】C
【解析】【解答】解:∵∠AOB与∠ACB都对 ,且∠AOB=100°,
∴∠ACB= ∠AOB=50°,
故选C
【分析】根据图形,利用圆周角定理求出所求角度数即可.
6.【答案】C
【解析】【解答】解:如图,连接OA、OB,过点O作OH垂直AB于点H,OH即为正六边形边心距.
∵六边形ABCDEF为正六边形
∴ ,OA=OB=AB=a,AH=BH= ,
∴
即半径为 的圆的内接正六边形的边心距是.
故答案为:C.
【分析】连接OA、OB,过点O作OH垂直AB于点H,OH即为正六边形边心距,根据正六边形的性质用勾股定理可求解.
7.【答案】B
【解析】【解答】解:∵,
∴AB=AC,
∴∠B=∠C=(180°-∠A)=(180°-30°)=75°.
故答案为B:.
【分析】利用同圆和等圆中,相等的弧所对的弦相等,可证得AB=AC,利用等边对等角及三角形的内角和定理可求出∠B的度数.
8.【答案】A
【解析】【解答】(1)、不符合题意,需要添加前提条件,即在同圆或等圆中;(2)、不符合题意,平分的弦不能是直径;(3)、不符合题意,等弧是指长度和度数都相等的弧;(4)、不符合题意,圆的对称轴是直径所在的直线.
故答案为:A.
【分析】在同圆或等圆中,相等的圆心角所对的弧相等,据此判断(1);平分弦(不是直径)的直径垂直于弦,据此判断(2);能重合的弧叫做等弧,据此判断(3);圆是轴对称图形,任何一条直径所在的直线都是对称轴,据此判断(4).
9.【答案】B
【解析】【解答】解:A、过不在同一直线上的三点能确定一个圆,正确,不符合题意;
B、平分弦(不是直径)的直径垂直于弦,故原命题错误,符合题意;
C、圆既是轴对称图形又是中心对称图形,正确,不符合题意;
D、相等的弧所对的弦相等,正确,不符合题意.
故答案为:B.
【分析】根据确定圆的条件可判断A;根据垂径定理可判断B;根据轴对称图形、中心对称图形的概念可判断C;根据弧、弦的关系可判断D.
10.【答案】B
【解析】【解答】解:如图连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4,
根据旋转不变性可知,A′B′=AB=4,
∴A′P=PB′,
∴PC= A′B′=2,
∵CM=BM=1,
又∵PM≤PC+CM,即PM≤3,
∴PM的最大值为3(此时P、C、M共线).
故答案为:B.
【分析】连接PC,根据∠A=30°,BC=2,可知AB的值,根据旋转的性质可知A′B′=AB,进而可知A′P、PB′、PC的知,结合图形和三角形三边关系即可得出PM的取值范围,进而可知P、C、M共线时,PM值最大,即可选出答案.
11.【答案】60
【解析】【解答】解:连接CC′,如图所示:
则B′、C′、C在一条直线上,
由旋转的性质得:∠1=∠2,DC′=DC,
∴∠3=∠4,
∵A′D′∥B′C′,
∴∠2=∠3,
∴∠1=∠3=∠4,
∴△CDC′是等边三角形,
∴∠CDC′=60°;
故答案为:60.
【分析】根据旋转的性质“对应点与旋转中心连线所成的角度都等于旋转的角度”可求解。
12.【答案】2.5
【解析】【解答】∵△DAE逆时针旋转90°得到△DCM,∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,∴DE=DM,∠EDM=90°,∴∠EDF+∠FDM=90°,∵∠EDF=45°,∴∠FDM=∠EDF=45°,
在△DEF和△DMF中, ,∴△DEF≌△DMF(SAS),∴EF=MF,设EF=MF=x,
∵AE=CM=1,且BC=3,∴BM=BC+CM=3+1=4,∴BF=BM﹣MF=BM﹣EF=4﹣x,
∵EB=AB﹣AE=3﹣1=2,在Rt△EBF中,由勾股定理得EB2+BF2=EF2, 即22+(4﹣x)2=x2,
解得:x= , ∴FM= .
【分析】 根据旋转的性质得出F、C、M三点共线,DE=DM,∠EDM=90°,进而得出∠FDM=∠EDF=45°,然后利用SAS判断出△DEF≌△DMF,根据全等三角形的对应边相等得出EF=MF,设EF=MF=x,然后根据勾股定理建立方程,求解即可得出答案
13.【答案】
【解析】【解答】解:∵旋转后AC的中点恰好与D点重合,即AD= AC′= AC,
∴在Rt△ACD中,∠ACD=30°,即∠DAC=60°,
∴∠DAD′=60°,∴∠DAE=30°,
∴∠EAC=∠ACD=30°,∴AE=CE.
在Rt△ADE中,设AE=EC=x,
则有DE=DC﹣EC=AB﹣EC=6﹣x,AD= ×6=2 ,
根据勾股定理得:x2=(6﹣x)2+(2 )2,
解得:x=4,∴EC=4,
则S△AEC= EC AD=4 .
故答案为:4 .
【分析】根据旋转的性质及中点的定义得出AD= AC′= AC,根据含30°直角三角形的边之间的关系得出在Rt△ACD中,∠ACD=30°,故DAC=60°,进而得出∠DAD′=60°,∠DAE=30°,∠EAC=∠ACD=30°,根据等角对等边得出AE=CE.在Rt△ADE中,设AE=EC=x,则有DE=DC﹣EC=AB﹣EC=6﹣x,AD=,根据UGG多了建立方程,求解得出x的值,然后滚局三角形的面积计算方算出答案。
14.【答案】
【解析】【解答】解:连接OD,分别作D点关于OB、OC的对称点M、N,连接OM、ON,MN,MN交OB于F,交OC于E,交OD于P,如图,
∵ED=EN,FM=FD,
∴△DEF的周长=ED+EF+FD=EN+EF+FM=MN,
∴此时△DEF的周长最小,
∵点D是 的中点,
∴∠BOD=∠COD= ∠BOC=30°,
∵M点与D点关于OB对称,
∴∠MOB=∠BOD=30°,OM=OD=2,
同理得∠NOC=∠COD=30°,ON=OD=2,
∵∠MON=120°,OM=ON=2,
而∠MOP=60°,
∴OP⊥MN,∠OMN=∠ONM=30°,
∴PM=PN,
在Rt△OPM中,OP= OM=1,
∴PM= OP= ,
∴MN=2PM=2 ,
∴△DEF周长的最小值为2 .
故答案为:2 .
【分析】连接OD,分别作D点关于OB、OC的对称点M、N,连接OM、ON,MN,MN交OB于F,交OC于E,交OD于P,如图,由ED=EN,FM=FD,得△DEF周长=ED+EF+FD=EN+EF+FM=MN,根据两点之间线段最短可知此时△DEF的周长最小.求出∠MON=120°,OM=ON=2,继而求出EF即可.
15.【答案】解:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
【解析】【分析】过O作OE⊥AB于点E,根据垂径定理可知CE=DE、AE=BE,利用等式性质即可证明。
16.【答案】解:连接OD.
∵CD⊥AB,
∴CE=DE= CD= (垂径定理),
故S△OCE=S△ODE,
∴S阴=S扇形OBD,
又∵∠CDB=30°,
∴∠COB=60°(圆周角定理),
∴OC=2,
故S扇形OBD= = ,
即阴影部分的面积为 .
【解析】【分析】根据圆的轴对称性可将阴影部分的面积转化为扇形OBD的面积,因此计算出扇形OBD面积即为所求。
17.【答案】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
点B旋转到点B2所经过的路径长为:=π.
故点B旋转到点B2所经过的路径长是π.
【解析】【分析】(1)根据网格特点,找出点A、B、C关于x轴的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)分别找出点A、B、C绕点O逆时针旋转90°的对应点A2、B2、C2的位置,然后顺次连接即可,观察可知点B所经过的路线是半径为,圆心角是90°的扇形,然后根据弧长公式进行计算即可求解.
18.【答案】解:△ABC是等边三角形.
证明如下:在⊙O中,
∵∠BAC与∠CPB是弧BC所对的圆周角,∠ABC与∠APC是弧AC所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°=∠ACB,
∴△ABC为等边三角形.
【解析】【分析】利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
19.【答案】(1)证明:如图,
∵PG平分∠EPF,
∴∠CPO=∠APO.
∵AO∥PD,
∴∠CPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO.
(2)解:过点O作OH⊥AB于H,如图.
根据垂径定理可得AH=BH=AB=6,
∴PH=PA+AH=AO+AH=10+6=16.
在Rt△AHO中,
OH==8,
∴tan∠OPB==.
∴tan∠OPB的值为.
【解析】【分析】(1)由PG平分∠EPF可得∠CPO=∠APO,由AO∥PD可得∠CPO=∠AOP,从而有∠APO=∠AOP,则有AP=AO.
(2)过点O作OH⊥AB于H,如图2.根据垂径定理可得AH=BH=6,从而可求出PH,在Rt△AHO中,运用勾股定理可求出OH,然后运用锐角三角函数的定义就可解决问题.
20.【答案】(1)证明:连接OD,如图所示.
∵DF是⊙O的切线,D为切点,
∴OD⊥DF,
∴∠ODF=90°
∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠CFD=∠ODF=90°,
∴DF⊥AC.
(2)解:∵∠CDF=30°,
由(1)得∠ODF=90°,
∴∠ODB=180°-∠CDF-∠ODF=60°
∵OB=OD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴BD弧的长=
【解析】【分析】(1)连接OD,先证明OD是△ABC的中位线,可得OD∥AC,求出∠CFD=∠ODF=90°,即可得到DF⊥AC;
(2)先证明△OBD是等边三角形, 可得∠BOD=60°,再利用弧长公式求出答案即可。
21.【答案】(1)证明:连接 ,
∵ ,
∴ ,
∵ ,
∴ ;
(2)解:∵ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
同理可得 ,
∴ .
【解析】【分析】(1)利用等弧所对的圆心角相等,可证得∠AOC=∠BOC;再利用角平分线上的点到角两边的距离相等,可证得CD=CE.
(2)利用∠AOB的度数,可求出∠OC=60°,从而可求出∠OCD=30°;再利用30°角所对的直角边等于斜边的一半,可求出CD的长;然后利用勾股定理求出CD的长,利用三角形的面积公式,可求出△CDO的面积.
22.【答案】(1)证明:
∵四边形是矩形,
∴,,
由旋转性质,得:,,
∴,,
∵在矩形中,,
∴,
在和中,
,
∴,
(2)解:∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∵,
∴,即的度数为.
【解析】【分析】(1)由矩形的性质可得,, , 结合旋转的性质可得推出 ,,,利用平行线的性质可得,根据AAS证明;
(2)根据矩形的性质可得, 利用全等三角形的性质及等腰三角形的性质可得,再根据直角三角形两锐角互余即可求解.
23.【答案】(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠PCD,
又∵∠A=∠P,
∴△ABC∽△PDC
(2)解:∵∠ABC=30°,AB=4,
∴BC= ,
∵△ABC∽△PDC,
∴∠D=∠ABC=30°,
∴CD=6
(3)解:如图,
∵AB是直径,∠ABC=30°,AB=4
∴∠ACB=90°,∠A=∠P=60°,AC=2,
∵CD⊥PC,
∴∠PCD=90°,CD=PC tan60°,
∵PC的最小值=AC=2,PC的最大值为直径=4,
∴CD的最小值为2 ,最大值为4 ,
∴2 ≤CD≤4
【解析】【分析】(1)利用圆周角定理,进而用"两角法"证出相似;(2)利用30度角的正切,由AB求出BC,再求出CD;(3)可用PC及三角函数表示出CD,当PC最小时,CD最小,CD最大,PC最大.
同课章节目录
