2.2二次函数的图像(2)
图片预览






文档简介
课件26张PPT。2.2 二次函数的图像(2)知识回顾:二次函数y=ax2的图象及其特点?1、顶点坐标?(0,0)2、对称轴?y轴(直线x=0)4、图象具有以下特点: 二次函数y=ax2( a≠0 )的图象是一条抛物线;
当a>0 时,抛物线开口向上,顶点是抛物线上的最低点;抛物线在x轴的上方(除顶点外)。
当a<0 时,抛物线开口向下,顶点是抛物线上的最高
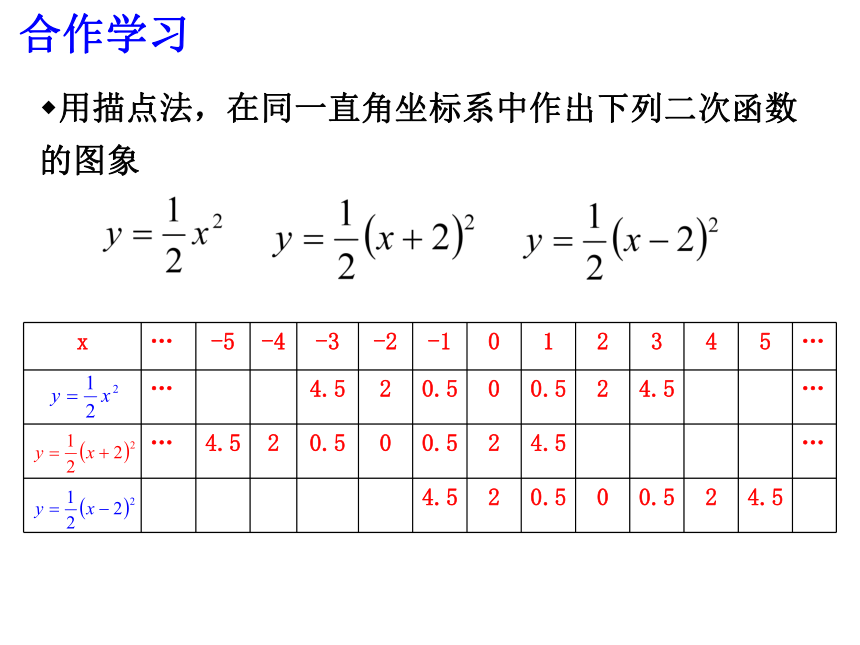
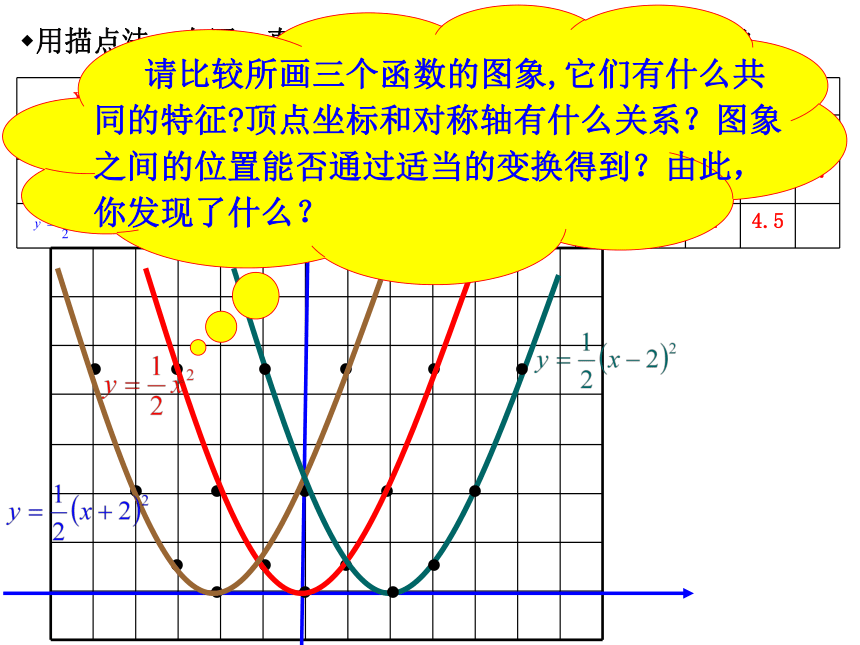
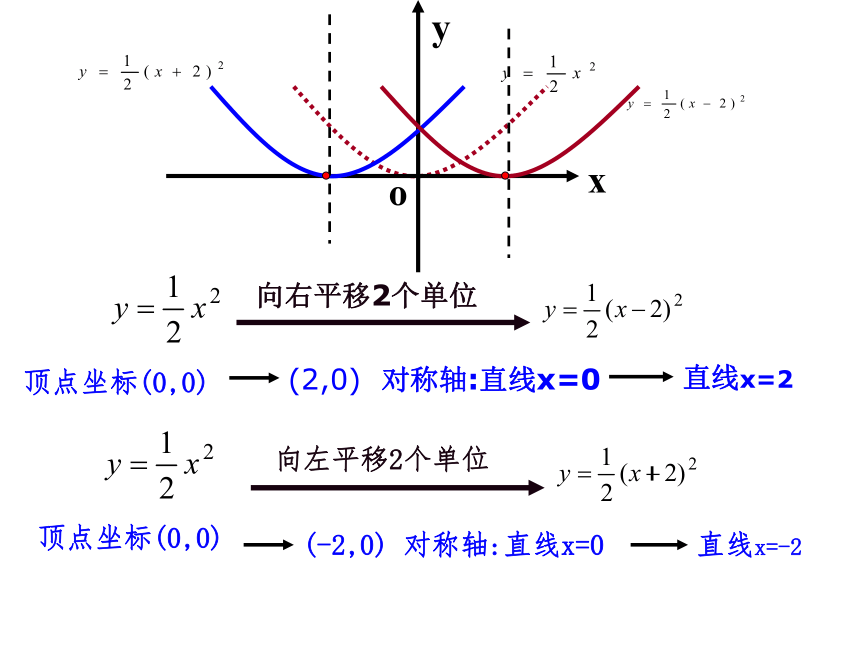
点:抛物线在x轴的下方(除顶点外)3、对称轴与抛物线的交点叫做抛物线的顶点用描点法,在同一直角坐标系中作出下列二次函数的图象合作学习用描点法,在同一直角坐标系中作出下列二次函数的图象....................................向左平移2个单位顶点(0,0)(-2,0)对称轴:直线x=0向左平移2个单位直线x=-2向右平移2个单位顶点坐标(0,0)(2,0)对称轴:直线x=0直线x=2向左平移2个单位顶点坐标(0,0)(-2,0)对称轴:直线x=0直线x=-2xyo.................. 1、请根据图象归纳一下二次函数y=a(x+m)2的性质;(顶点坐标,对称轴,开口方向,最高点和最低点)2、请归纳出二次函数y=a(x+m)2与y=ax2之间的位置关系;填写下表: (2,0)
直线x=2
向上
有最低点(0,0)
Y轴
向上
有最低点 (-2,0)
直线x=-2
向上
有最低点 (-m,0)
直线x=-m
a>0向上,
a<0,向下
a>0最低点,
a<0最高点y=ax2y=a(x+m)2m>0,向左平移m个单位m<0,向右平移[m]个单位请你总结二次函数y=a(x+ m)2的图象和性质. 当m>0时,向左平移当m<0时,向右平移a>0时,开口________, 最 ____ 点是顶点; a<0时,开口________, 最 ____ 点是顶点;
对称轴是 _____________,
顶点坐标是 __________。直线x=-m(-m,0)的图象2)顶点坐标是(3,0),对称轴是直线x=3.1、对于二次函数 请回答下列问题:(2)说出函数 的图象的顶点坐标
和对称轴。(1)把函数 的图象作怎样的平移
变换,就能得到函数 的图象。练一练向上直线x=-3( -3 , 0 )直线x=1直线x=3向下向下( 1 , 0 )( 3, 0)3、填空:
(1)由抛物线y=2x2向 平移 个单位可得到y= 2(x+1)2
(2)函数y= -5(x -4)2 的图象。可以由抛物
线 向 平移 4 个单位而得到的。2、填写下表:左右y=-5x21例2、用描点法在同一直角坐标系中画出函数
的图象 . 经过怎样平移得到思考:完成下表:(其中a>0)(0,0)Y轴向上(0,k)(-m.0)(-m,k)Y轴直线x=-m向上向上向上直线x=-m当m>0时,向左平移当m<0时,向右平移当k>0时向上平移当k<0时向下平移顶点坐标和开口方向与a、m、k因此,二次函y=a(x+m)2+km左正右负 k上正下负的值有关。 一般地,平移二次函数 的图象就
可得到二次函数y=a(x+m)2+k的图象 它的形状、对称轴、 一般地函数y=a(x+m)2+k的图象,函数y=ax2的图象只是位置不同,
(1)可以由y=ax2的图象先向右(当m<0)或向左(当m>0)平移∣m∣个单位,再向上(当k>0)或向下(当k<0)平移∣k∣个单位得到,
(2)顶点坐标是(—m,k),对称轴是直线x=-m,
(3)图象在x轴的上方还是下方,开口方向向上还是向下等性质由y=ax2来决定的。函数y=a(x+m)2+k的图象的性质:共同归纳:1、函数y= 3(x - 2)2 + 1的图象。
可以由抛物线 向 平移 个单位,
再向 平移 个单位而得到的。
它的顶点坐标 对称轴是直线 ;做一做y=3x2右2上1(2,1)x=22、指出下列二次函数的开口方向、对称轴和顶点坐标:3、填空:
(1)由抛物线y=2x2向 平移 个单位,
再向 平移 个单位可得到y= 2(x +1)2 –3。
(2)函数y= 3(x - 2)2 + ?的图象。
可以由抛物线 向 平移 个单位,
再向 平移 个单位而得到的。
做一做练习一 说一说1.下列函数是通过什么抛物线怎样平移得到的?并指出它的顶点坐标、对称轴、增减性、 x为何值时y有最值及最值是什么?
(1)y=2x2+1 (2)y=-2-5x22、把抛物线y=-x2向上平移2个单位,得到的抛物线是 ;3、把抛物线y=-3x2+2向下平移k个单位,得到的抛物线的
解析式为y=ax2-3,则a= ,k= 。4、对于抛物线y=1+2x2,下列说法是否正确?
(1)顶点为(1,0) (2)对称轴是y轴
(3)当x=0时,y取得最小值是1
(4)当x<0时,y随x的增大而减小这节课你有什么收获和体会?2、 如果一条抛物线的形状与
的形状相同,且顶点坐标是(4,-2)
则函数关系式是__________能力拓展35、><<<=>>>>6、0
当a>0 时,抛物线开口向上,顶点是抛物线上的最低点;抛物线在x轴的上方(除顶点外)。
当a<0 时,抛物线开口向下,顶点是抛物线上的最高
点:抛物线在x轴的下方(除顶点外)3、对称轴与抛物线的交点叫做抛物线的顶点用描点法,在同一直角坐标系中作出下列二次函数的图象合作学习用描点法,在同一直角坐标系中作出下列二次函数的图象....................................向左平移2个单位顶点(0,0)(-2,0)对称轴:直线x=0向左平移2个单位直线x=-2向右平移2个单位顶点坐标(0,0)(2,0)对称轴:直线x=0直线x=2向左平移2个单位顶点坐标(0,0)(-2,0)对称轴:直线x=0直线x=-2xyo.................. 1、请根据图象归纳一下二次函数y=a(x+m)2的性质;(顶点坐标,对称轴,开口方向,最高点和最低点)2、请归纳出二次函数y=a(x+m)2与y=ax2之间的位置关系;填写下表: (2,0)
直线x=2
向上
有最低点(0,0)
Y轴
向上
有最低点 (-2,0)
直线x=-2
向上
有最低点 (-m,0)
直线x=-m
a>0向上,
a<0,向下
a>0最低点,
a<0最高点y=ax2y=a(x+m)2m>0,向左平移m个单位m<0,向右平移[m]个单位请你总结二次函数y=a(x+ m)2的图象和性质. 当m>0时,向左平移当m<0时,向右平移a>0时,开口________, 最 ____ 点是顶点; a<0时,开口________, 最 ____ 点是顶点;
对称轴是 _____________,
顶点坐标是 __________。直线x=-m(-m,0)的图象2)顶点坐标是(3,0),对称轴是直线x=3.1、对于二次函数 请回答下列问题:(2)说出函数 的图象的顶点坐标
和对称轴。(1)把函数 的图象作怎样的平移
变换,就能得到函数 的图象。练一练向上直线x=-3( -3 , 0 )直线x=1直线x=3向下向下( 1 , 0 )( 3, 0)3、填空:
(1)由抛物线y=2x2向 平移 个单位可得到y= 2(x+1)2
(2)函数y= -5(x -4)2 的图象。可以由抛物
线 向 平移 4 个单位而得到的。2、填写下表:左右y=-5x21例2、用描点法在同一直角坐标系中画出函数
的图象 . 经过怎样平移得到思考:完成下表:(其中a>0)(0,0)Y轴向上(0,k)(-m.0)(-m,k)Y轴直线x=-m向上向上向上直线x=-m当m>0时,向左平移当m<0时,向右平移当k>0时向上平移当k<0时向下平移顶点坐标和开口方向与a、m、k因此,二次函y=a(x+m)2+km左正右负 k上正下负的值有关。 一般地,平移二次函数 的图象就
可得到二次函数y=a(x+m)2+k的图象 它的形状、对称轴、 一般地函数y=a(x+m)2+k的图象,函数y=ax2的图象只是位置不同,
(1)可以由y=ax2的图象先向右(当m<0)或向左(当m>0)平移∣m∣个单位,再向上(当k>0)或向下(当k<0)平移∣k∣个单位得到,
(2)顶点坐标是(—m,k),对称轴是直线x=-m,
(3)图象在x轴的上方还是下方,开口方向向上还是向下等性质由y=ax2来决定的。函数y=a(x+m)2+k的图象的性质:共同归纳:1、函数y= 3(x - 2)2 + 1的图象。
可以由抛物线 向 平移 个单位,
再向 平移 个单位而得到的。
它的顶点坐标 对称轴是直线 ;做一做y=3x2右2上1(2,1)x=22、指出下列二次函数的开口方向、对称轴和顶点坐标:3、填空:
(1)由抛物线y=2x2向 平移 个单位,
再向 平移 个单位可得到y= 2(x +1)2 –3。
(2)函数y= 3(x - 2)2 + ?的图象。
可以由抛物线 向 平移 个单位,
再向 平移 个单位而得到的。
做一做练习一 说一说1.下列函数是通过什么抛物线怎样平移得到的?并指出它的顶点坐标、对称轴、增减性、 x为何值时y有最值及最值是什么?
(1)y=2x2+1 (2)y=-2-5x22、把抛物线y=-x2向上平移2个单位,得到的抛物线是 ;3、把抛物线y=-3x2+2向下平移k个单位,得到的抛物线的
解析式为y=ax2-3,则a= ,k= 。4、对于抛物线y=1+2x2,下列说法是否正确?
(1)顶点为(1,0) (2)对称轴是y轴
(3)当x=0时,y取得最小值是1
(4)当x<0时,y随x的增大而减小这节课你有什么收获和体会?2、 如果一条抛物线的形状与
的形状相同,且顶点坐标是(4,-2)
则函数关系式是__________能力拓展35、><<<=>>>>6、0
同课章节目录
