2.2等腰三角形性质,

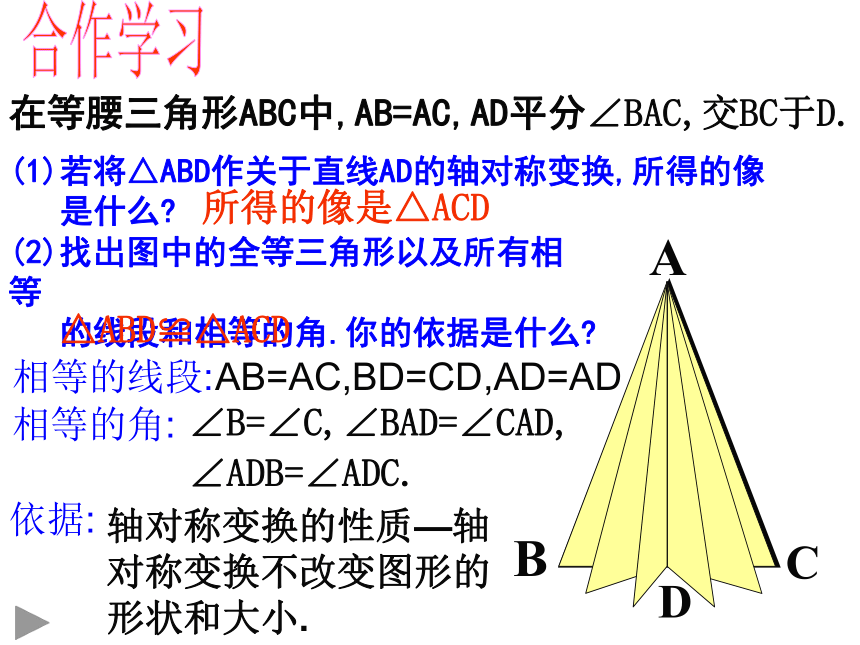
课件24张PPT。2.2等腰三角形的性质 将一把三角尺和一个重锤如图放置，就能检查一根横梁是否水平，你知道检验的方法吗？想一想合作学习在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于D.(1)若将△ABD作关于直线AD的轴对称变换,所得的像
是什么?(2)找出图中的全等三角形以及所有相等
的线段和相等的角.你的依据是什么?所得的像是△ACD△ABD≌△ACD相等的线段:AB=AC,BD=CD,AD=AD相等的角:∠B=∠C,∠BAD=∠CAD,
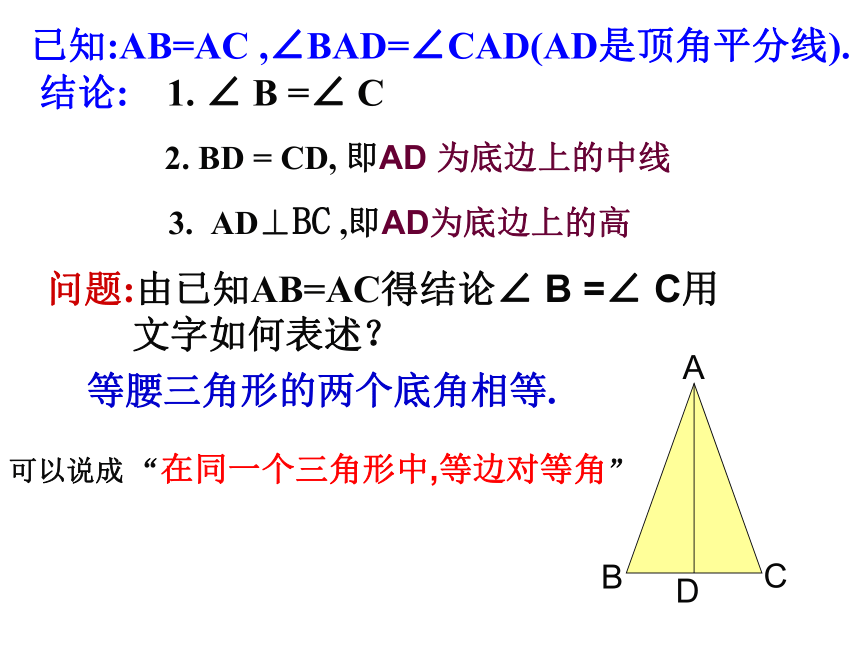
∠ADB=∠ADC.依据:轴对称变换的性质—轴对称变换不改变图形的形状和大小. 1. ∠ B =∠ C 2. BD = CD, 即AD 为底边上的中线3. AD⊥BC ,即AD为底边上的高问题:由已知AB=AC得结论∠ B =∠ C用
文字如何表述？等腰三角形的两个底角相等.已知:AB=AC ,∠BAD=∠CAD(AD是顶角平分线).可以说成 “在同一个三角形中,等边对等角”结论: 等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.简称“等腰三角形三线合一”如果已知AB=AC,AD⊥BC(AD是底边上的高).
那么有什么结论?如果已知AB=AC,BD=CD (AD是底边
上的中线).那么有什么结论?等腰三角形的性质:顶角平分线底边上的中线底边上的高BD=CD(AD是底边上的中线),
∠BAD=∠CAD(AD是顶角平分线).AD⊥BC(AD是底边上的高),
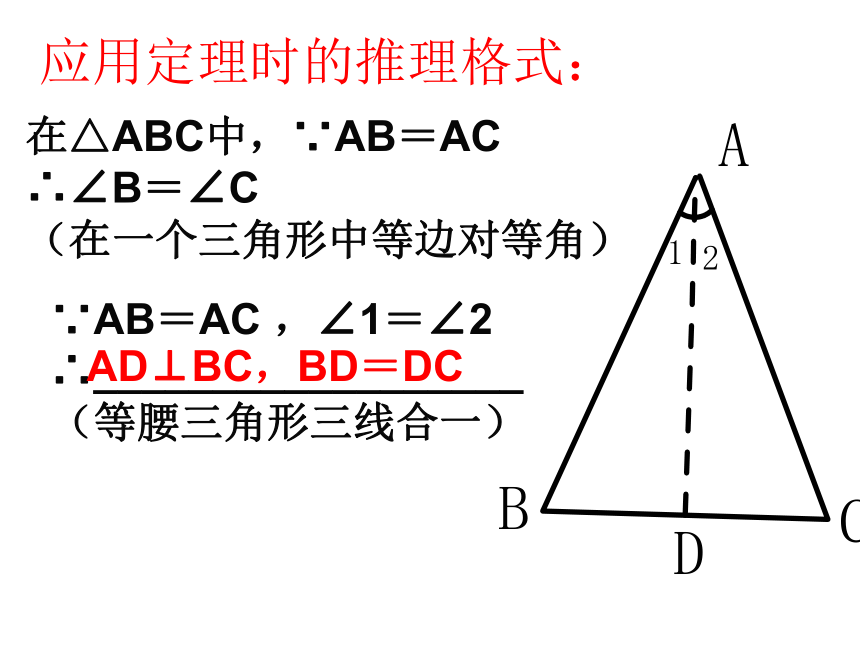
∠BAD=∠CAD(AD是顶角平分线)演示应用定理时的推理格式： 在△ABC中，∵AB＝AC
∴∠B＝∠C
（在一个三角形中等边对等角） ∵AB＝AC ，∠1＝∠2
∴__________________
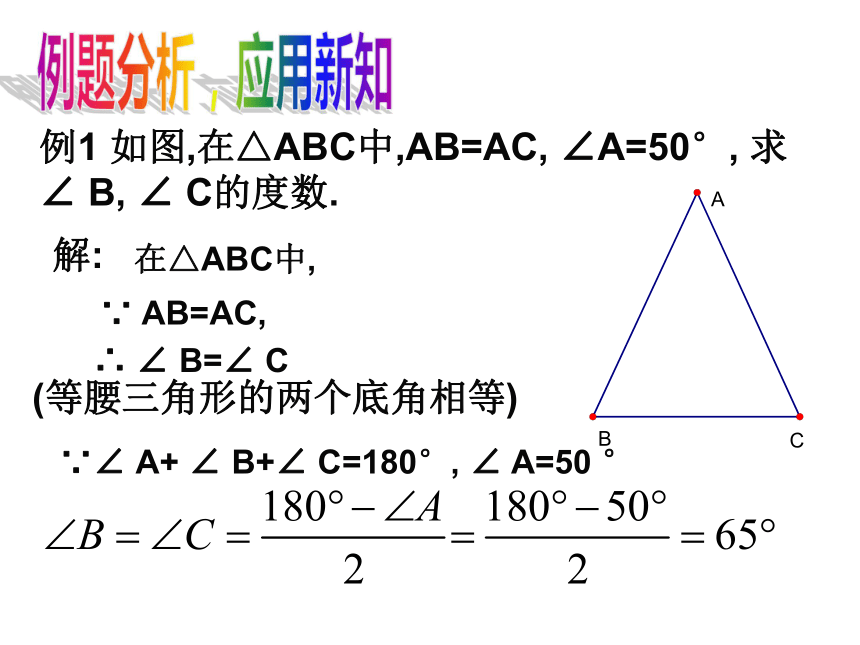
（等腰三角形三线合一）AD⊥BC，BD＝DC 将一把三角尺和一个重锤如图放置，就能检查一根横梁是否水平，你知道为什么吗？想一想例题分析，应用新知例1 如图,在△ABC中,AB=AC, ∠A=50°, 求∠ B, ∠ C的度数. 解:在△ABC中,∵ AB=AC,∴ ∠ B=∠ C(等腰三角形的两个底角相等)∵∠ A+ ∠ B+∠ C=180°, ∠ A=50 ° ①.等腰三角形的一个顶角为36°，则它的底角是____
②等腰三角形的一个底角为36°，则它的顶角是_____
③等腰三角形的一内角为40°，则它的顶角是_____小试牛刀72°108°40°或100°1.等腰三角形一个角为70°,它的另外两个角
.2.等腰三角形一个角为110°,它的另外两个角
为___________.① 顶角+2×底角=180°② 顶角=180°－2×底角③ 底角=（180°－顶角）÷2④0°＜顶角＜180°
⑤0°＜底角＜90°结论:在等腰三角形中,35 °，35 °70°,40° 或 55°,55° 小试牛刀∵AB=AC，∠1=∠2
∴________________AD⊥BC, BD=CD∵AB=AC，AD⊥BC
∴________________∠1=∠2 ,BD=CD∵AB=AC，
∴∠1=∠2 , AD⊥BC几何语言：__________BD=CD如图所示，已知点D、E在BC上，AB=AC,AD=AE.说明BD=CE的理由。 练一练例2 已知线段a, h(如图),用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.作法如图，已知∠α和线段a,用直尺和圆规作一个等腰三角形，使它的顶角等于∠α，底边上的中线等于a。举一反三28页 书上作业题第4题判断下列语句是否正确。1.等腰三角形的角平分线、中线和高互相重合。（ ）
2.有一个角是60°的等腰三角形，其它两个内角也为60°. （ ）
3.等腰三角形的底角都是锐角. （ ）
4.钝角三角形不可能是等腰三角形 . ( ）××作业巩固练习巩固练习1.填空题：
(1)如图,在△ ABC中,AB=AC,外角∠ ACD=100,则∠ B=____度
　 变式
（1）等腰三角形的一内角为100°，则它的顶角是_____
（2）等腰三角形的一外角为100°，则它的底角是_____巩固练习(2)如图,在等腰三角形ABC中,AB=AC,D为BC的中点,则点D到AB,AC的距离相等.请说明理由.
　 （3）.已知在△ABC中，AB＝AC，直线AE交BC于点D，O是AE上一动点但不与A重合，且OB＝OC，试猜想AE与BC的关系，并说明你的猜想的理由. 巩固练习文字叙述几何语言等腰三角形的两底角相等（简称等边对等角）∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边（简称三线合一）∵AB=AC，∠1=∠2 ∴AD⊥BC， BD=CD课堂小结拓展提高∠∠1. 作业本2.23. 预习2.3, 下节课带好直尺、圆规等2. 教与学2.2作业布置4、对于等腰三角形两腰上的高、中线、两底角的平分线，它们各自之间会不会存在某种关系？请你作出猜想，并利用所学知识说明为什么？ACB