2.4二次函数的应用(1)

课件25张PPT。2.4 二次函数的应用(1)1、二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值？2、如何求二次函数的最值？3、求下列函数的最大值或最小值：
①y=x2-4x+7 ②y=-5x2+8x-1温故知新：配方法公式法1、求下列二次函数的最大值或最小值：
y=－x2＋4xy =-(x2-4x)= =-(x2-4x+22-22)=－(x－2)2＋4所以：当x=2时，y 达到最大值为4.解：因为 －1＜0，则图像开口向下，y有最大值当x= 时，
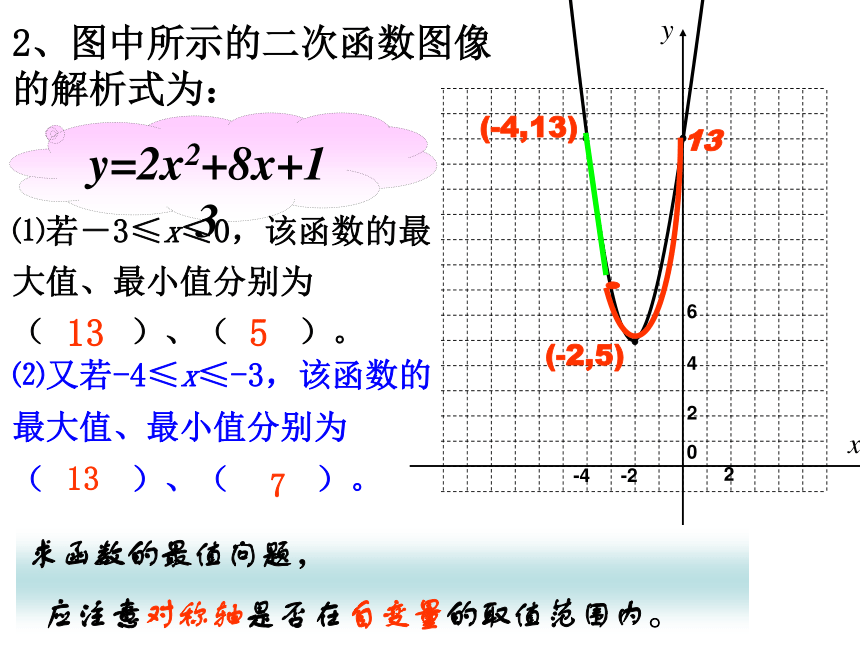
y达到最大值为温故知新：2、图中所示的二次函数图像的解析式为： y=2x2+8x+13⑴若－3≤x≤0，该函数的最大值、最小值分别为（ ）、（ ）。⑵又若-4≤x≤-3，该函数的最大值、最小值分别为（ ）、（ ）。求函数的最值问题，
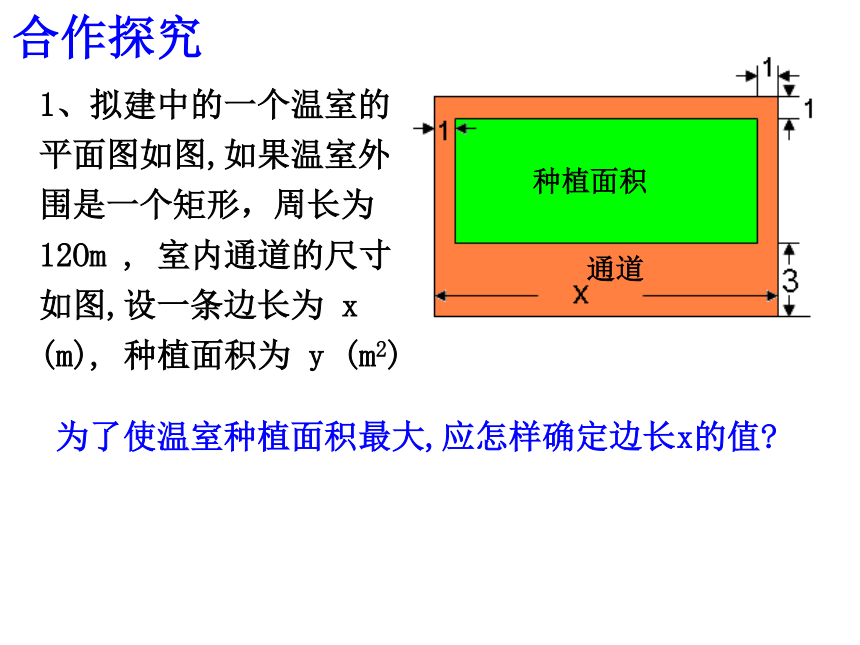
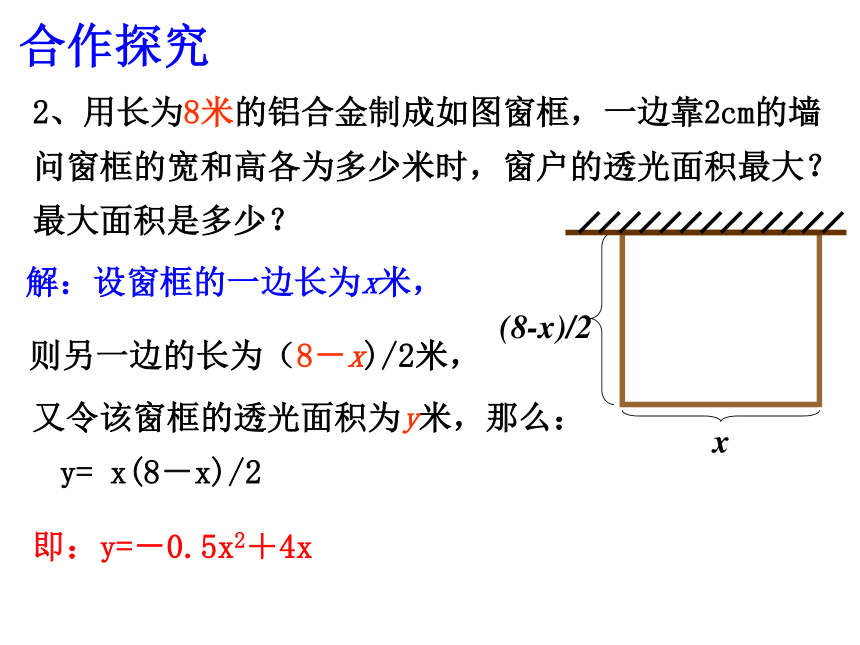
应注意对称轴是否在自变量的取值范围内。131313(-4,13)(-2,5)57 为了使温室种植面积最大,应怎样确定边长x的值?合作探究2、用长为8米的铝合金制成如图窗框，一边靠2cm的墙问窗框的宽和高各为多少米时，窗户的透光面积最大？最大面积是多少？解：设窗框的一边长为x米，x(8-x)/2又令该窗框的透光面积为y米，那么：y= x(8－x)/2即：y=－0.5x2＋4x则另一边的长为（8－x)/2米，合作探究 3、用长为8米的铝合金制成如图窗框，问窗框的宽和高各多少米时，窗户的透光面积最大？最大面积是多少？合作探究解：设矩形窗框的面积为y,由题意得，小结：应用二次函数的性质解决日常生活中的最值问题，一般的步骤为：①把问题归结为二次函数问题（设自变量和函数）；③在自变量的取值范围内求出最值；②求出函数解析式（包括自变量的取值范围）；④答。 已知，直角三角形的两直角边的和为2，求斜边长可能达到的最小值，以及当斜边长达到最小值时两条直角边的长。解：设其中的一条直角边长为x，则另一条直角边长为（2－x），, 又设斜边长为y，所以：当x＝1时，(属于0斜边长有最小值y= ,
此时两条直角边的长均为1其中0状相同的抛物线落下。建立如图所示的坐标系，如果喷头所在
处A（0，1.25），水流路线最高处B（1，2.25），则该抛物线
的表达式为 。如果不考虑其他因素，那么水
池的半径至少要____米，才能使喷出的水流不致落到池外。y= －(x-1)2 +2.252.53、如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称． ⑴钢缆的最低点到桥面的距离是 ；
⑵两条钢缆最低点之间的距离是 ；
(3)右边的抛物线解析式是 ；1米40米 例2、已知铅球所经过的路线是某个二次函数图像的一部分，如图所示，如果这个男同学的出手处A点的坐标(0，2)，铅球路线的最高处B点的坐标为(6，5) (1)求这个二次函数的解析式； (2)该男同学把铅球推出去多远？(精确到0.01米 ) .yox24862461012B(6,5)A(0,2)C(?,2/3)(2,-10)分析:（1）在给出的直角坐标系中，要确定抛物线的解析式，就要确定抛物线上三个点的坐标. 起跳点O（0,0），入水点（2,－10），最高点的纵点标为 2/3??. (0,0) ??????????? ??或 ??????????? 又∵抛物线对称轴在y轴右侧
所以a,b异号
故:2（2）在某次试跳中，测得运动员在空中的运动路线是（1）中的抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为18/5米，问此次跳水会不会失误？并通过计算说明理由。(2)当运动员在空中距池边的水平距离为18?/5?米,即?x= 18/5 -?2=8/5时因此，此次跳水会失误. ∴此时运动员距水面的高为 如图，隧道横截面的下部是矩形，上部是半圆，周长为16米。
⑴求截面积S（米2）关于底部宽x（米）的函数解析式，及自变量x 的取值范围？⑵试问：当底部宽x为几米时，隧道的截面积S最大（结果精确到0.01米）？解：∵隧道的底部宽为x，周长为16，答：当隧道的底部宽度为4.48米时，隧道的截面积最大。做一做收获：学了今天的内容，你最深的感受是什么？实际问题抽象转化数学问题运用数学知识问题的解返回解释检验 1、如图所示，已知抛物线y=ax2+bx+c(a≠0)与x轴相交于两点A（x1，0） B（x2，0）（x1 已知有一张边长为10cm的正三角形纸板，若要从中剪一个面积最大的矩形纸板，应怎样剪？最大面积为多少？再见