2.3 二次函数的性质

(共38张PPT)
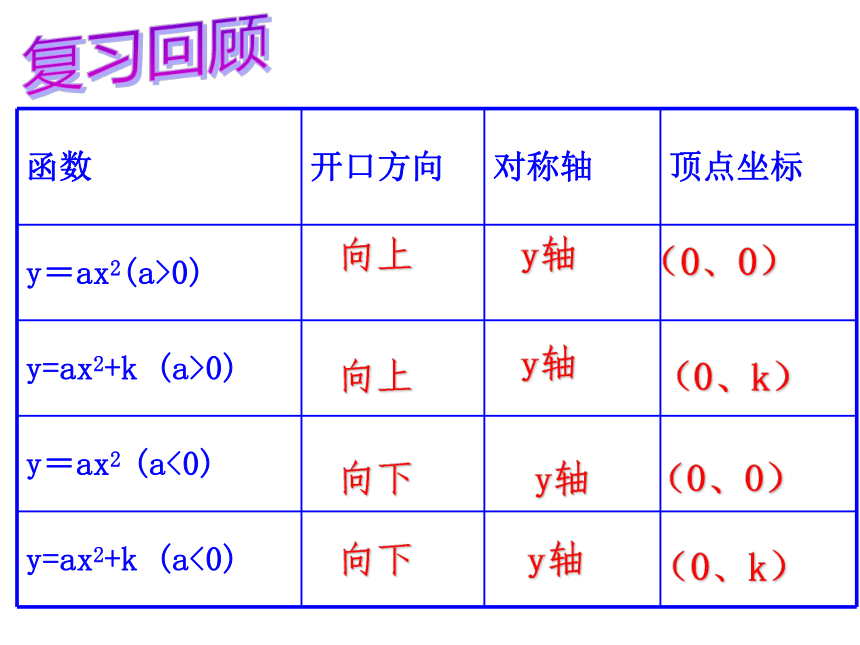
函数 开口方向 对称轴 顶点坐标
y＝ax2(a>0)
y=ax2+k (a>0)
y＝ax2 (a<0)
y=ax2+k (a<0)
向上
向上
向下
向下
y轴
y轴
y轴
y轴
（0、0）
（0、0）
（0、k）
（0、k）
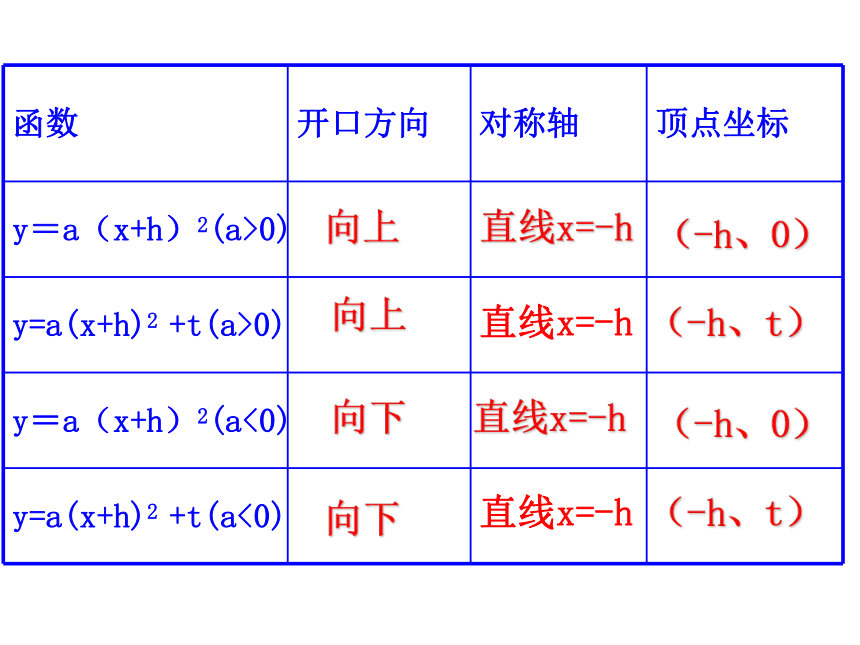
函数 开口方向 对称轴 顶点坐标
y＝a（x+h）2(a>0)
y=a(x+h)2 +t(a>0)
y＝a（x+h）2(a<0)
y=a(x+h)2 +t(a<0)
向上
直线x=-h
（-h、0）
向下
直线x=-h
（-h、0）
向上
向下
直线x=-h
（-h、t）
直线x=-h
（-h、t）
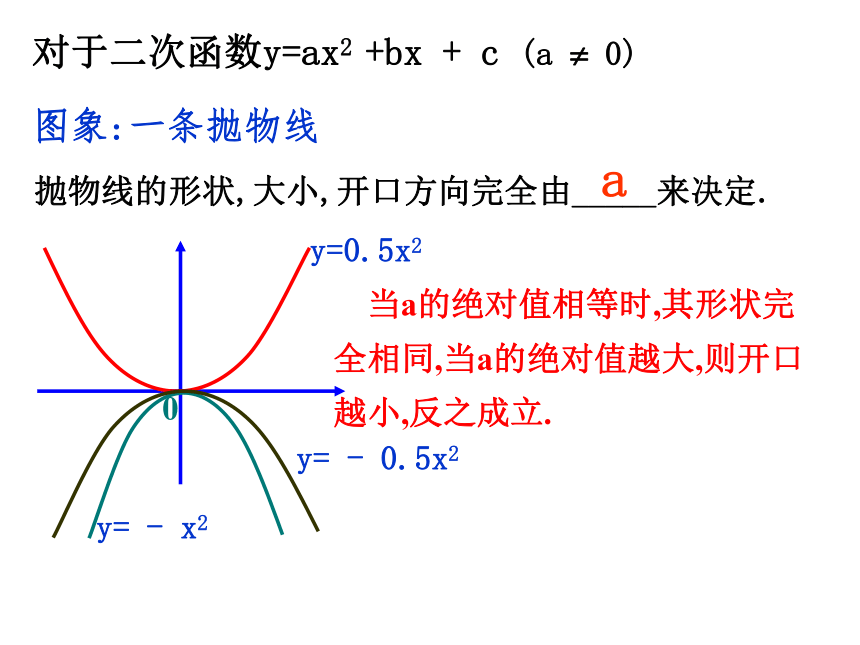
对于二次函数y=ax2 +bx + c (a 0)
图象:一条抛物线
抛物线的形状,大小,开口方向完全由_____来决定.
当a的绝对值相等时,其形状完全相同,当a的绝对值越大,则开口越小,反之成立.
0
y=0.5x2
y= - x2
y= - 0.5x2
a
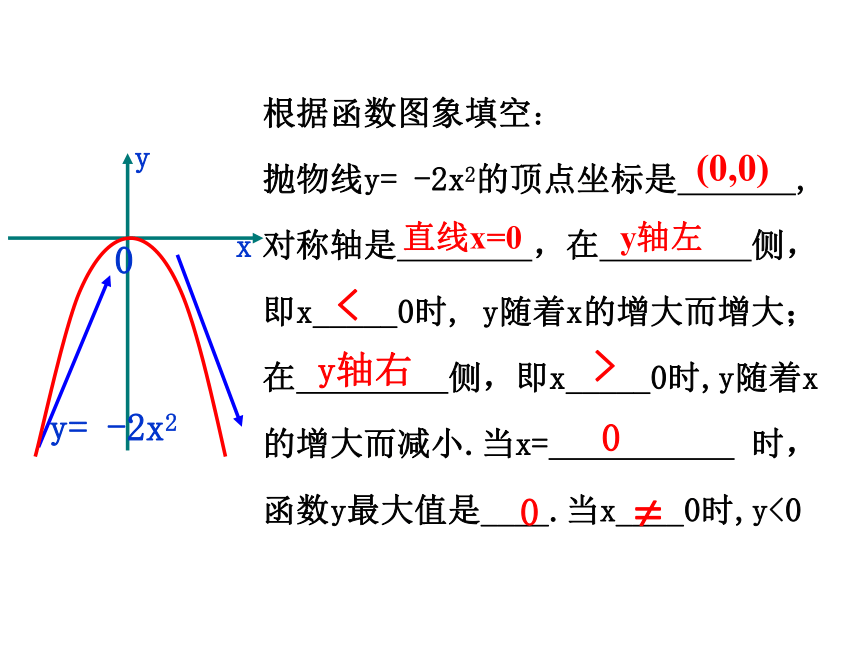
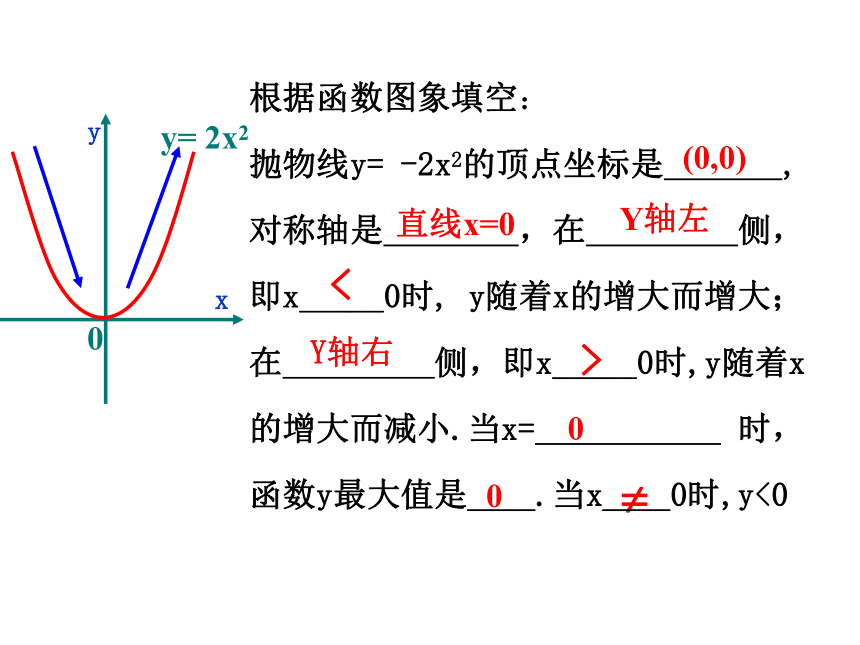
根据函数图象填空：
抛物线y= -2x2的顶点坐标是 ,对称轴是 ，在 侧，即x_____0时, y随着x的增大而增大；在 侧，即x_____0时,y随着x的增大而减小.当x= 时，函数y最大值是____.当x____0时,y<0
(0,0)
直线x=0
y轴右
y轴左
0
0
<
>

0
y= -2x2
y
x
(0,0)
直线x=0
Y轴右
Y轴左
0
0
<
>

0
y= 2x2
y
x
根据函数图象填空：
抛物线y= -2x2的顶点坐标是 ,对称轴是 ，在 侧，即x_____0时, y随着x的增大而增大；在 侧，即x_____0时,y随着x的增大而减小.当x= 时，函数y最大值是____.当x____0时,y<0
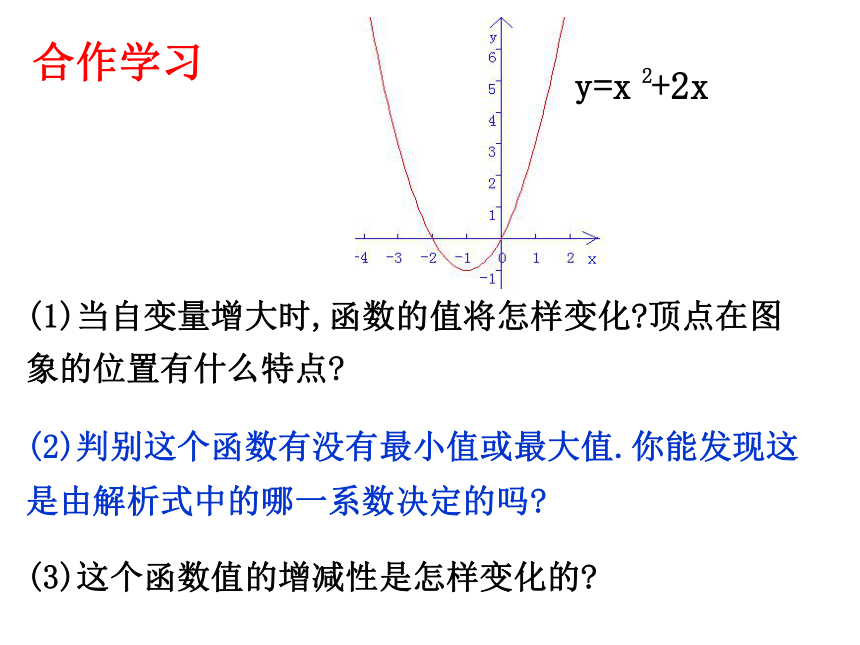
函数 y=ax2+bx+c 基本性质回顾
二次函数y=ax2+bx+c（a≠0）的图像是一条抛物线
y=x +2x
2
合作学习
(1)当自变量增大时,函数的值将怎样变化 顶点在图象的位置有什么特点
(2)判别这个函数有没有最小值或最大值.你能发现这是由解析式中的哪一系数决定的吗
(3)这个函数值的增减性是怎样变化的
x
y
0
2
-2
-2
2
-4
y
x
0
2
4
6
-2
2
-4
4
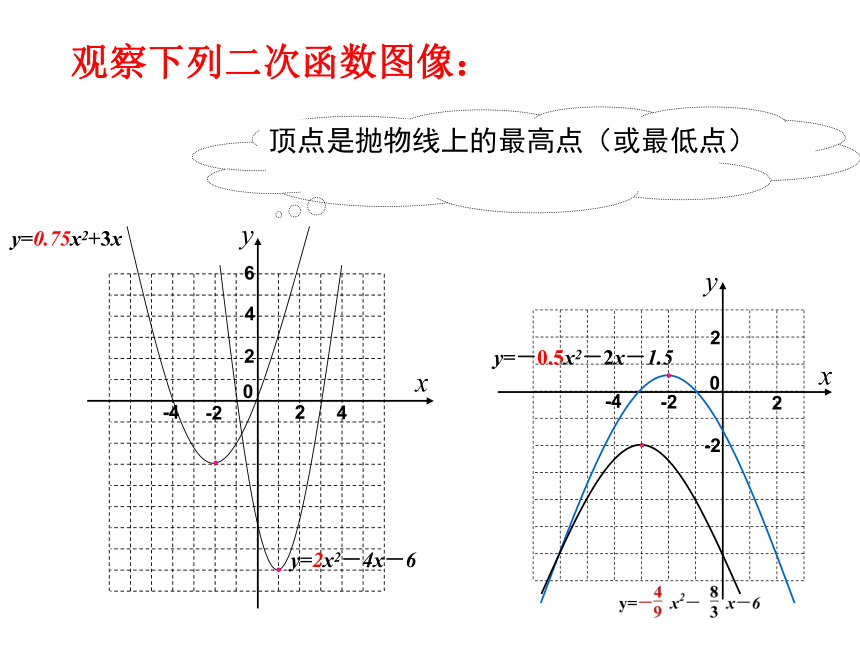
y=2x2－4x－6
y=0.75x2+3x
y=－0.5x2－2x－1.5
观察下列二次函数图像：
顶点在图像的位置有什么特点？
顶点是抛物线上的最高点（或最低点）
条件 图像 增减性 最大（小）值
x
y
o
x2
x1
x
y
o
x1
x2
二次函数y=ax2+bx+c(a≠0)的性质：
a＞0
a＜ 0
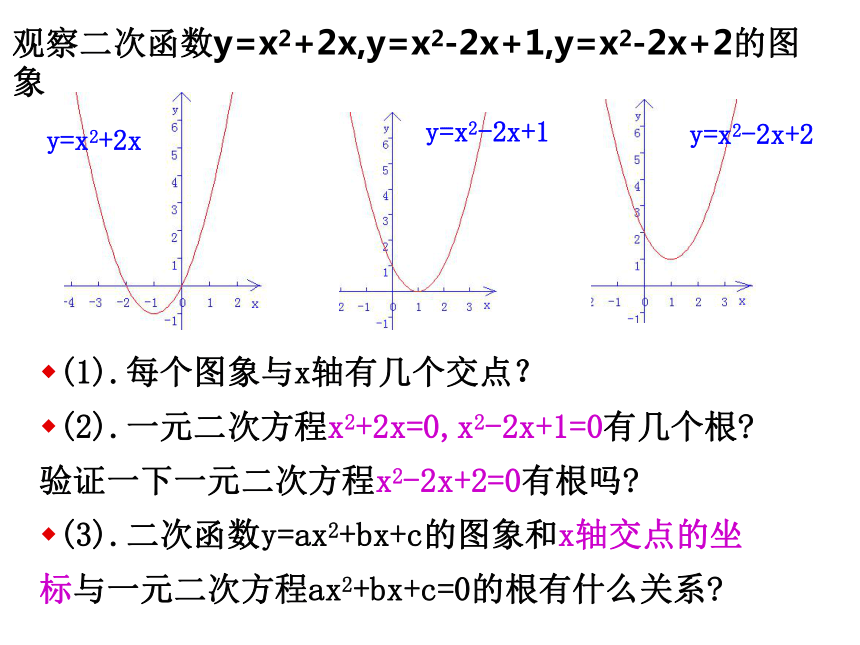
(1).每个图象与x轴有几个交点？
(2).一元二次方程x2+2x=0,x2-2x+1=0有几个根 验证一下一元二次方程x2-2x+2=0有根吗
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
观察二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象
y=x2+2x
y=x2-2x+1
y=x2-2x+2
求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。
解：∵A、B在x轴上，
∴它们的纵坐标为0，
∴令y=0，则x2-3x+2=0
解得：x1=1，x2=2；
∴A（1，0） ， B（2，0）
你发现方程 的解x1、x2与A、B的坐标有什么联系？
x2-3x+2=0
举例:
结论：方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此，抛物线与一元二次方程是有密切联系的。
如果二次函数y=ax2+bx+c (a≠0)的图像与x轴的两个交点的 坐标为 （ x1，0 ）和（ x2 ，0）
方程ax2+bx+c＝0 (a≠0)的解与二次函数y=ax2+bx+c (a≠0)的图像与x轴交点的坐标有什么关系？
那么x1和 x2 恰好是方程ax2+bx+c＝0 (a≠0)的两个根
方程ax2+bx+c＝0 (a≠0)的解就是
函数y=ax2+bx+c (a≠0)的图像与x轴交点的 坐标。
横
可以发现：二次函数y=ax2+bx+c (a≠0)的图像与x轴交点的 存在性与
方程ax2+bx+c＝0 (a≠0)的
解是否存在有关。
合作探究
那么，进一步推想方程ax2+bx+c＝0 (a≠0)解的存在性又与什么有关呢？
b2 －4ac的正负性有关。
故而：
①当b2 －4ac 时，抛物线与x轴 交点；
②当b2 －4ac 时，抛物线与x轴只有 交点；
③当b2 －4ac 时，抛物线与x轴 交点。
＞0 两个
＝0 一个
＜0 没有
例1、已知函数y=－0.5x2－7x＋7.5
(1)求函数的顶点坐标、对称轴，以及图像与坐标轴的交点 坐标，并画出函数的大致图像；
解：（1）∵a=－0.5,b=－7,c=7.5;
所以函数y=－0.5x2－7x＋7.5的大致图像如图：
x=－7
20
x
y
10
O
10
－10
30
5
－10
－20
－15
－5
(－7，32)
(0，7.5)
(－15，0)
(1，0)
⑵自变量x在什么范围内时，y随x 的增大而增大？何时y 随x的增大而减小？并求出函数的最大值或最小值。
解： ⑵由右图可知，当x≤－7 时 ， y随x 的增大而增大；
当x≥－7 时，y 随x的增大而减小；
当x＝－7时，函数有最大值32。
(-15,0)
(1,0)
(0,7.5)
(-7,32)
(-14,7.5)
.
0
x
y
(3）根据第（１）题的图象草图，说 出 x 取哪些值时，① y=0; ② y<0; ③ y>0.
x=-15或x=1
x<-15或x>1
-15A
B
C
S⊿ABC=0.5×AB×OC=0.5×16×7.5=60
(4)求图象与坐标轴交点构成的三角形的面积：
x
o
y
(0,c)
函数图像的顶点、图像与坐标轴的交点，以及图像与y轴的交点关于图象对称轴的对称点。
x
o
y
(0,c)
y=ax2+bx+c
X=-b/2a
练一练
1、求下列函数的最大值（或最小值）和对应的自变量的值：
⑴ y=2x2－8x＋1；
⑵ y=－3x2－5x＋1
解： ⑴ ∵y=2x2－8x＋1＝2(x－2)2－7
∴当x=2时,y有最小值,为－7
⑵ ∵a=－3＞0且b=－5,c=1;
故:当x= 时，y有最 值，为
大
配方法
公式法
2、已知函数y=x2－3x－4.
⑴求函数图像的顶点坐标、与坐标轴交点的坐标和对称轴，并画出函数的大致图像；
解：∵ y=x2－3x－4 ＝(x－1.5)2－6.25,
∴图象顶点坐标为(1.5, －6.25);
又当y=0时，
得x2－3x－4＝0的解为：
x1＝－1，x2＝4。
则与x轴的交点为(－1,0)和(4,0)
与y轴的交点为(0, －4)
(－1,0)
(1.5, －6.25)
(0, －4)
(4,0)
x=1.5
O
y
x
(－1,0)
(1.5, －6.25)
(0, －4)
(4,0)
x=1.5
O
y
x
⑵记当x1=1.5, x2= , x3= 时对应的函数值分别为y1,y2,y3,试比较y1,y2,y3的大小
( ,y2)
( ,y3)
(3.5,y1)
x=
x=
x=3.5
(2)在二次函数y=x2-3x-4中,自变量x_______时,y随x 的增大而增大,
x______时,y随x的增大而减小.
≥1.5
≤1.5
∵ < <1.5
即x2∴y1例2、二次函数y=ax2+bx+c(a≠0)的图象如图所示，则a、b、c的符号分别怎样？　　　　　　
y
x
o
1、已知二次函数的图像如图所示，下列结论：
⑴a+b+c﹤0 ⑵a-b+c﹥0 ⑶abc ﹥0 ⑷b=2a
其中正确的结论的个数是（ ）
A、1个 B、2个 C、3个 D、4个
2、下列函数何时有最大值或最小值，并求出最大值或最小值
⑴ y=2x2-8x-3 ⑵ y=-5x２＋３√２x- 4
3、二次函数y=x2＋bx+8的图像顶点在x轴的负半轴上，那么b等于多少？
D
-1
1
0
x
y
做一做
例3、如图，在ΔABC中，AB=8cm，BC=6cm，∠B＝90°，点P从点A开始沿AB边向点B以2厘米／秒的速度移动，点Q从点B开始沿BC边向点C以1厘米／秒的速度移动，如果P,Q分别从A,B同时出发，几秒后ΔPBQ
的面积最大？最大面积是多少？
A
B
C
P
Q
解：根据题意，设经过x秒后ΔPBQ的面积y最大,则：
AP=2x cm PB=（8-2x ） cm
QB=x cm
则： y=1/2 x（8-2x）
=-x2 +4x
=-（x2 -4x +4 -4）
= -（x - 2）2 + 4
所以，当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2
（0A
B
C
P
Q
1、已知抛物线经过点(3,0),(2,-3),并以直线x=0为对称轴 (1)求这条抛物线的解析式. (2)求出这个二次函数的最大值或最小值. (3)在此抛物线上有两点A(x1,y1),B(x2,y2),且x1>x2>0,试比较y1与y2的大小.
2、如图直线l经过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图像在第一象限内相交于P点,若△AOP的面积为4.5,求二次函数的解析式.
A
B
P
O
x
y
3、将抛物线y=x2向下平移后,使它的顶点C与它在x轴上的两个交点A,B组成等边三角形ABC,求此抛物线的解析式。
　谈谈你的收获、感受？！
1、如图，等腰Rt△ABC的直角边AB＝２，点P、Q分别从A、C两点同时出发，以相等的速度作直线运动，已知点P沿射线AB运动，点Q沿边BC的延长线运动，PQ与直线相交于点D。
(1)设 AP的长为x，△PCQ的面积为S，求出S关于x的函数关系式
(2)当AP的长为何值时，S△PCQ= S△ABC
解：１）∵P、Q分别从A、C两点同时出发，速度相等
∴AP=CQ=x
当P在线段AB上时
S△PCQ＝
CQ PB
=
AP PB
即S＝ (0课外拓展
当P在线段AB的延长线上时
S△PCQ＝
即S＝　 (x>2）
(2)当S△PCQ＝S△ABC时，有
＝２
此方程无实数根
②　 ＝２
　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　
∴ x1=1+ , x2=1－ (舍去)
∴当AP长为1+ 时，S△PCQ＝S△ABC
3.05米
4米

2.25米
o
x
y
⑴球运动路线的函数解析式和自变量的取值范围
⑵球在运动中离地面的最大高度。
解: ⑴设函数解析式为:
y=a(x－2.5)2+k,根据题意，得：
2.52a+k=2.25
(4－2.5)2a+k=3.05
则：a=－0.2,k=3.5
∴解析式为:y=－0.2x2+x+2.25,
自变量x的取值范围为：0≤x≤4.
⑵球在运动中离地面的最大高度为3.5米。
2、篮球运动员投篮时，球运动的路线为抛物线的一部分（如图），抛物线的对称轴为x=2.5。求：