3.4 简单几何体的表面展开图 (2) 课件 22张ppt
文档属性
| 名称 | 3.4 简单几何体的表面展开图 (2) 课件 22张ppt |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-05 16:55:42 | ||
图片预览




文档简介
(共22张PPT)
浙教版九年级下册
第三章 三视图与表面展开图
3.4 简单几何体的表面展开图 (2)
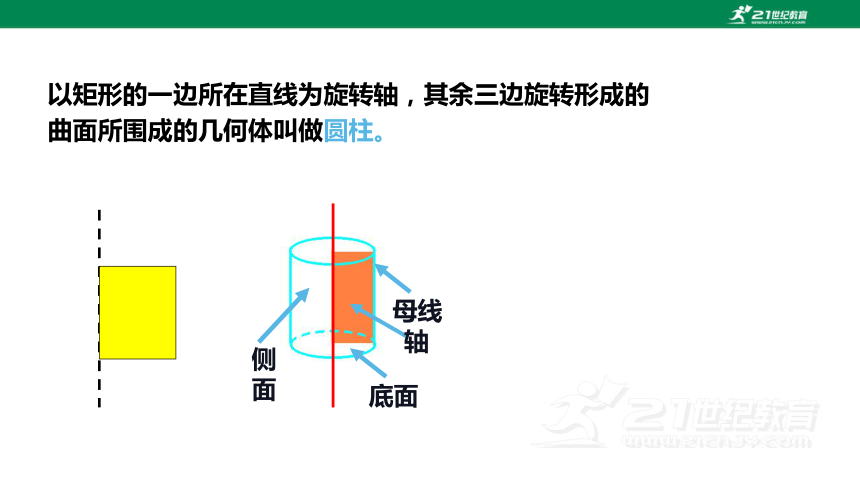
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
底面
侧面
母线
轴
如图,圆柱可以看作矩形ABCD绕边BC所在直线___________,其余各边所成的面围成的几何体。
AB,CD旋转所成的面就是 ,
是两个半径相同的圆。
AD旋转所成的面就是 。
AD不论转到哪个位置,都是 .
旋转一周
圆柱的两个底面
圆柱的侧面
圆柱的母线
1.圆柱是由两个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面.
2.与圆柱两底面垂直的线段叫做圆柱的母线
3.圆柱两个底面圆心的距离圆柱的高
问题:圆柱的母线有几条?
圆柱的母线与圆柱的高有什么关系?
圆柱有无数条母线
圆柱的母线长=圆柱的高的长
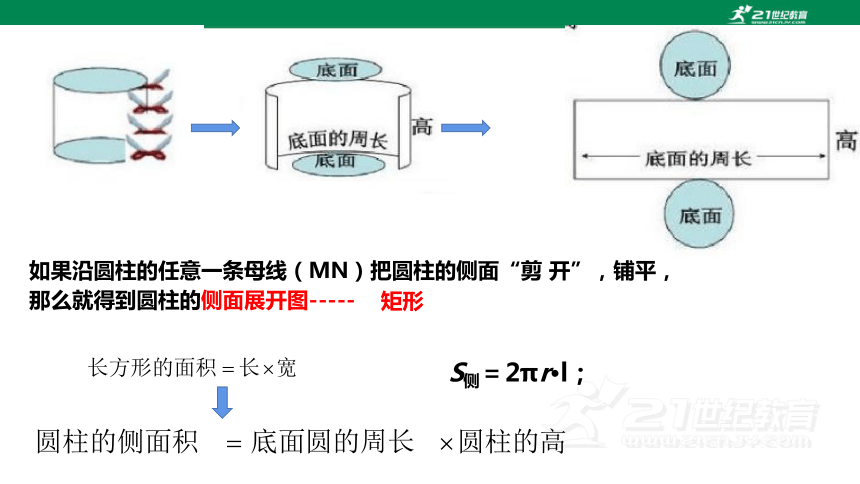
如果沿圆柱的任意一条母线(MN)把圆柱的侧面“剪 开”,铺平,
那么就得到圆柱的侧面展开图-----
S侧=2πr·l;
矩形
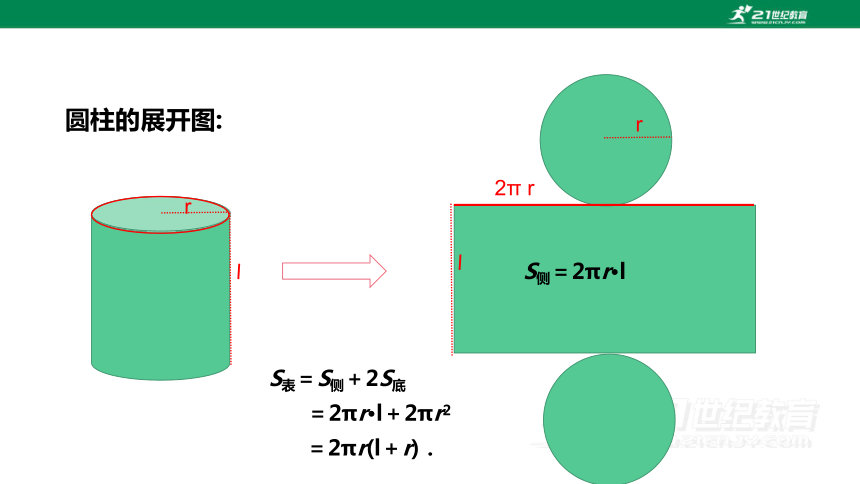
圆柱的展开图:
r
l
l
2π r
r
S侧=2πr·l
S表=S侧+2S底
=2πr·l+2πr2
=2πr(l+r).
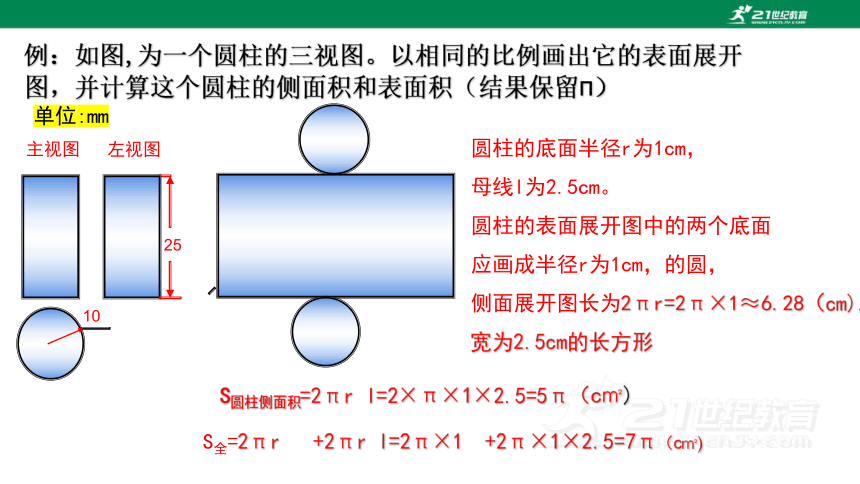
例:如图,为一个圆柱的三视图。以相同的比例画出它的表面展开图,并计算这个圆柱的侧面积和表面积(结果保留π)
圆柱的底面半径r为1cm,
母线l为2.5cm。
圆柱的表面展开图中的两个底面
应画成半径r为1cm,的圆,
侧面展开图长为2πr=2π×1≈6.28(cm),
宽为2.5cm的长方形
25
单位:mm
左视图
10
主视图
S圆柱侧面积=2πr l=2×π×1×2.5=5π(c㎡)
S全=2πr +2πr l=2π×1 +2π×1×2.5=7π(c㎡)
S圆柱侧面积=底面圆的周长×圆柱母线长
S圆柱侧面积=2πr l
S圆柱侧面积=2πr l+ 2πr2
S圆柱表面积=圆柱侧面积+2×底面积
公式
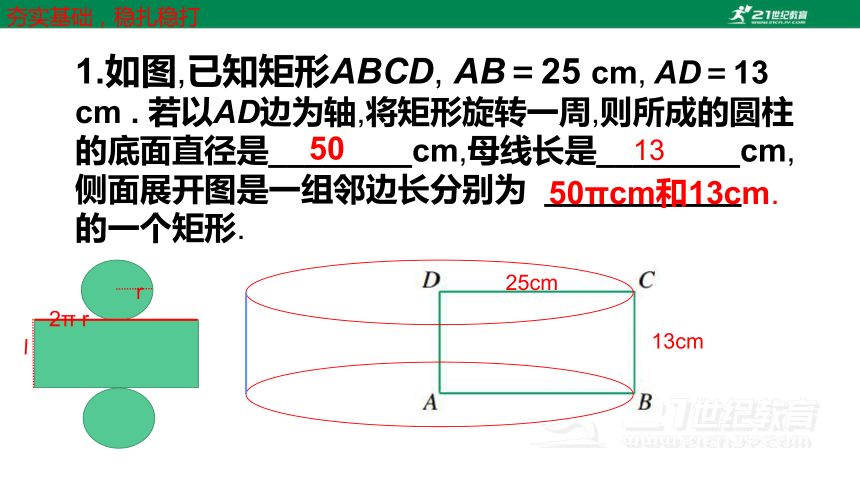
1.如图,已知矩形ABCD, AB=25 cm, AD=13 cm . 若以AD边为轴,将矩形旋转一周,则所成的圆柱的底面直径是________cm,母线长是________cm,侧面展开图是一组邻边长分别为 ___________ 的一个矩形.
50
夯实基础,稳扎稳打
25cm
50πcm和13cm.
13
13cm
l
2π r
r
2.一个圆柱的底面直径为20cm,母线长为15cm.求这个圆柱的侧面积和全面积(结果保留π).
S側= 2πrl = 2π×10×15= 300π(cm2).
S全= 2πr + 2πrl = 2π×10 +2π×10×15 = 500π(cm2).
2π r
l
3.一个圆柱的底面半径为120mm,母线长为280mm.以1:10的比例画出它的表面展开图,并求出它的侧面积和
全面积(结果保留π).
S側= 2πrl = 2π×120×280 =67200π(mm2).
S全= 2πr + 2πrl = 96000π(mm2).
2π r
l
4.已知圆柱的全面积为150πcm ,母线长为10 cm.求这个圆柱的底面半径.
解:设底面积半径为 r.由题意,
得 2πr + 2πr×10 = 150π,
∴ r +10r-75 = 0,
解得r 1= 5,r2=15 (不合题意,舍去).
答:圆柱的底面半径为5cm.
底面
底面
底面的周长
底面
底面
底面的周长
高
高
5.已知一个圆柱的侧面展开图是长为20πcm,宽为10cm的矩形.描述这个圆柱的形状,并画出它的三视图(尺寸比例自选).
底面
底面
底面的周长
底面
底面
底面的周长
高
高
2πr=20π
r=10 (cm)
6.已知一个圆柱的底面半径r与母线长l的比为2:3,圆柱的全面积为500πcm .选取适当的比例画出这个圆柱的表面展开图.
2πr + 2πr×r = 500π.
=
2l=3r
l=
.
r =100.
解得r1= 10,r2=-10 (不合,舍去) .
∴ l=15.
A
B
7. 在底面半径为1、高为2的圆柱体的左下角A处有一只蚂蚁,
欲从圆柱体的侧面爬行去吃右上角B处的食物,问怎样爬行路径最短,
最短路径是多少?
A
从A点向上剪开,则侧面展开图如图所示,
连接AB,则AB为爬行的最短路径.
最短路径:
连续递推,豁然开朗
B
8.如图,一油桶高2米,底面半径1 米,一只壁虎由A到B吃一害虫,
欲从圆柱体的侧面爬行一周,需要爬行的最短路程是多少
A
B
A
B
最短路径:
9.如图,圆柱形容器中,高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为________(容器厚度忽略不计)
1.3m
思维拓展,更上一层
A
B
小河
A'
0.5
1.2
1.3
10.请阅读下列材料:
问题:如图(1)一圆柱的底面半径、高均为5 cm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC.如图(2)所示:设路线1的长度为l1,
则l12=AC2=AB2+BC2=52+(5π)2=25+25π2.
路线2:高线AB+底面直径BC.如图(1)所示:设路线2的长度为l2,
则l22=(AB+BC)2=(5+10)2=225
l12-l22=25+25π2-225=25π2-200=
25(π2-8)>0
∴l12>l22,∴l1>l2
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1 cm,
高AB为5 cm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2=__________
路线2:l22=(AB+BC)2=____
∵l12____l22,
∴l1____l2,(填“>”或“<”)
∴选择路线____(填“1”或“2”)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线较短.
25+π2
49
<
<
1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版九年级下册
第三章 三视图与表面展开图
3.4 简单几何体的表面展开图 (2)
以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫做圆柱。
底面
侧面
母线
轴
如图,圆柱可以看作矩形ABCD绕边BC所在直线___________,其余各边所成的面围成的几何体。
AB,CD旋转所成的面就是 ,
是两个半径相同的圆。
AD旋转所成的面就是 。
AD不论转到哪个位置,都是 .
旋转一周
圆柱的两个底面
圆柱的侧面
圆柱的母线
1.圆柱是由两个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面.
2.与圆柱两底面垂直的线段叫做圆柱的母线
3.圆柱两个底面圆心的距离圆柱的高
问题:圆柱的母线有几条?
圆柱的母线与圆柱的高有什么关系?
圆柱有无数条母线
圆柱的母线长=圆柱的高的长
如果沿圆柱的任意一条母线(MN)把圆柱的侧面“剪 开”,铺平,
那么就得到圆柱的侧面展开图-----
S侧=2πr·l;
矩形
圆柱的展开图:
r
l
l
2π r
r
S侧=2πr·l
S表=S侧+2S底
=2πr·l+2πr2
=2πr(l+r).
例:如图,为一个圆柱的三视图。以相同的比例画出它的表面展开图,并计算这个圆柱的侧面积和表面积(结果保留π)
圆柱的底面半径r为1cm,
母线l为2.5cm。
圆柱的表面展开图中的两个底面
应画成半径r为1cm,的圆,
侧面展开图长为2πr=2π×1≈6.28(cm),
宽为2.5cm的长方形
25
单位:mm
左视图
10
主视图
S圆柱侧面积=2πr l=2×π×1×2.5=5π(c㎡)
S全=2πr +2πr l=2π×1 +2π×1×2.5=7π(c㎡)
S圆柱侧面积=底面圆的周长×圆柱母线长
S圆柱侧面积=2πr l
S圆柱侧面积=2πr l+ 2πr2
S圆柱表面积=圆柱侧面积+2×底面积
公式
1.如图,已知矩形ABCD, AB=25 cm, AD=13 cm . 若以AD边为轴,将矩形旋转一周,则所成的圆柱的底面直径是________cm,母线长是________cm,侧面展开图是一组邻边长分别为 ___________ 的一个矩形.
50
夯实基础,稳扎稳打
25cm
50πcm和13cm.
13
13cm
l
2π r
r
2.一个圆柱的底面直径为20cm,母线长为15cm.求这个圆柱的侧面积和全面积(结果保留π).
S側= 2πrl = 2π×10×15= 300π(cm2).
S全= 2πr + 2πrl = 2π×10 +2π×10×15 = 500π(cm2).
2π r
l
3.一个圆柱的底面半径为120mm,母线长为280mm.以1:10的比例画出它的表面展开图,并求出它的侧面积和
全面积(结果保留π).
S側= 2πrl = 2π×120×280 =67200π(mm2).
S全= 2πr + 2πrl = 96000π(mm2).
2π r
l
4.已知圆柱的全面积为150πcm ,母线长为10 cm.求这个圆柱的底面半径.
解:设底面积半径为 r.由题意,
得 2πr + 2πr×10 = 150π,
∴ r +10r-75 = 0,
解得r 1= 5,r2=15 (不合题意,舍去).
答:圆柱的底面半径为5cm.
底面
底面
底面的周长
底面
底面
底面的周长
高
高
5.已知一个圆柱的侧面展开图是长为20πcm,宽为10cm的矩形.描述这个圆柱的形状,并画出它的三视图(尺寸比例自选).
底面
底面
底面的周长
底面
底面
底面的周长
高
高
2πr=20π
r=10 (cm)
6.已知一个圆柱的底面半径r与母线长l的比为2:3,圆柱的全面积为500πcm .选取适当的比例画出这个圆柱的表面展开图.
2πr + 2πr×r = 500π.
=
2l=3r
l=
.
r =100.
解得r1= 10,r2=-10 (不合,舍去) .
∴ l=15.
A
B
7. 在底面半径为1、高为2的圆柱体的左下角A处有一只蚂蚁,
欲从圆柱体的侧面爬行去吃右上角B处的食物,问怎样爬行路径最短,
最短路径是多少?
A
从A点向上剪开,则侧面展开图如图所示,
连接AB,则AB为爬行的最短路径.
最短路径:
连续递推,豁然开朗
B
8.如图,一油桶高2米,底面半径1 米,一只壁虎由A到B吃一害虫,
欲从圆柱体的侧面爬行一周,需要爬行的最短路程是多少
A
B
A
B
最短路径:
9.如图,圆柱形容器中,高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为________(容器厚度忽略不计)
1.3m
思维拓展,更上一层
A
B
小河
A'
0.5
1.2
1.3
10.请阅读下列材料:
问题:如图(1)一圆柱的底面半径、高均为5 cm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的线段AC.如图(2)所示:设路线1的长度为l1,
则l12=AC2=AB2+BC2=52+(5π)2=25+25π2.
路线2:高线AB+底面直径BC.如图(1)所示:设路线2的长度为l2,
则l22=(AB+BC)2=(5+10)2=225
l12-l22=25+25π2-225=25π2-200=
25(π2-8)>0
∴l12>l22,∴l1>l2
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1 cm,
高AB为5 cm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2=__________
路线2:l22=(AB+BC)2=____
∵l12____l22,
∴l1____l2,(填“>”或“<”)
∴选择路线____(填“1”或“2”)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线较短.
25+π2
49
<
<
1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
