3.1圆 (1)

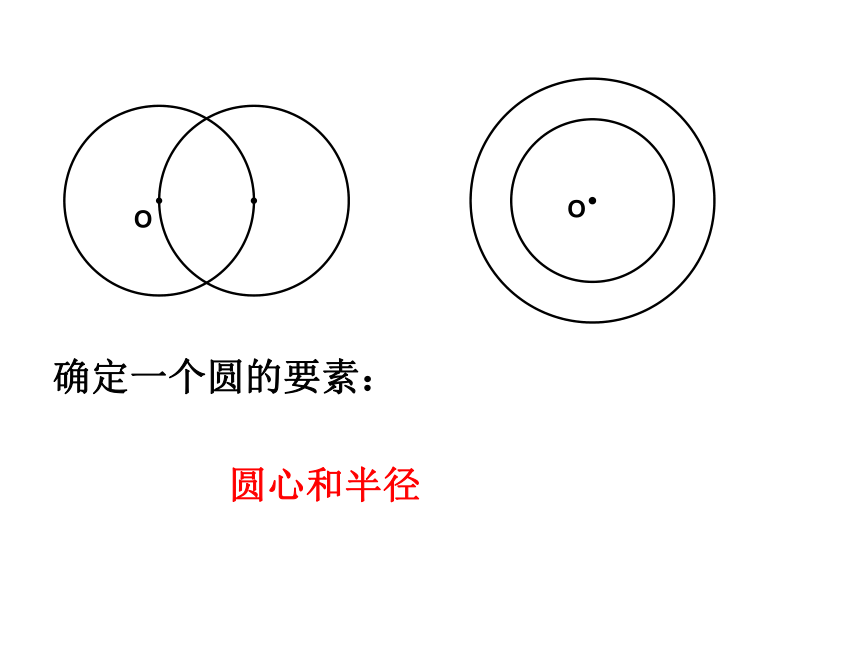
课件29张PPT。3.1 圆（1）一石激起千层浪奥运五环福建土楼小憩片刻祥子生活离不开圆乐在其中圆圆圆的画法请在白纸上画一个半径为2cm的圆． 若要在平坦的操场上画一个半径为3m的圆,你有什么办法? 线段OP绕它固定的一个端点O旋转一周，另一端点P所经过的封闭曲线叫做圆。封闭曲线定点O叫做圆心。线段OP叫做圆的半径。在同一平面内，定义确定一个圆的要素：圆心和半径做一做1、已知点O和线段a，请以O为圆心，线段a为半径做一个圆，并在圆上画出一条半径，一条直径和一条不是直径的弦；2、作一个半径为1.5cm 的圆，然后画出一条直径，一条不等于直径的弦，再用字母和符号表示弦所对的两条弧；1、请写出图中所有的弦；2、请任选一条弦，写出这条弦所对的弧；弦与弧连结圆上任意两点的线段，叫弦；经过圆心的弦叫直径；直径是半径的两倍；圆上任意两点间的部分叫做圆弧，简称弧（arc）；圆的任意一条直径的两个端点分圆成两条弧，都叫半圆小于半圆的弧叫劣弧（minor arc），大于半圆的弧叫优弧（major arc）；弦与弧的表示法及读法 请将自己所画的圆与同伴所画的圆进行比较， 它们是否能够完全重合？并思考什么情况下两个圆能够完全重合？半径相等的两个圆叫做等圆。 请再作一个圆与已知圆是等圆，并使其中一个圆通过另一个圆的圆心。O下列命题中，哪些是真命题？哪些是假命题？辨一辨(1)弦是直径；(2)圆上的任意两点都能将圆分成一条劣弧和一条优弧；(4)半径相等的圆一定能重合；(3)圆中优弧所对的弦一定比劣弧所对的弦长；假命题假命题假命题真命题(5)一个圆有且只有一条直径.假命题OABC⊙O的半径为r =3m。若A，B，C三位同学分别站在如图所示的位置。问:这三个同学所站的位置与圆有怎样的位置关系,用什么去判定呢?请思考O 如图，设⊙O的半径为r，点到圆心的距离为d。d＝r若点A在圆上，则：若点C在圆外，则：d＞r若点B在圆内，则：d＜rABC疑:反之是否成立?点与圆的位置关系如图，设⊙O的半径为r，A点在圆内，B点在圆上，C点在圆外，那么OA＜r， OB＝r， OC＞r．反过来也成立，即 点的位置可以确定该点到圆心的距离与半径的关系，反过来，已知点到圆心的距离与半径的关系可以确定该点到圆的位置关系。归纳性质： 一般地，如果用r表示圆的半径，d表示同一平面内点到圆心的距离，则有：已知⊙O的面积为25π。（1）若PO=5.5，则点P在 ；（2）若PO=4，则点P在 ；（3）若PO= ，则点P在圆上。圆外圆内5填一填投圈游戏 如果老师和我们班的同学正在做投圈游戏, 我们呈“一”字型排开,这样的队形对每个人公平吗?你认为我们应当排成什么样的队形? 例1、如图所示，在A地正北80m的Ｂ处有一幢民房，正西100m的C处有一变电设施，在BC的中点D处是一古建筑。 因施工需要，必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏，问爆破影响面的半径应控制在什么范围内？解：连结AD∵∠BAC=Rt∠∴BC2=AC2+AB2=1002+802=16400∴BC=∴AD=∴AD＜AB＜AC答：爆破影响面的半径应小于10 。 1、在直角三角形ABC中，∠C=Rt∠，AC=3cm，AB=5cm。若以点C为圆心，画一个半径为3cm的圆，试判断点A，点B和⊙C的相互位置关系。练一练2、如图，在A岛附近，半径约250km的范围内是一暗礁区，往北300km有一灯塔Ｂ，往西400km有一灯塔C。现有一渔船沿CB航行，问渔船会进入暗礁区吗？D练一练3、一个点到已知圆上的点的最大距离是8，最小距离是2，则圆的半径是多少？练一练课堂小结　　请把你本节课的所学，所想，所得作一归纳，与同伴共同分享！ 1、如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 拓展提高2、如图,一根6m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域. 63、一个8×10米的长方形草地，现要安装自动喷水装置,这种装置喷水的半径为5米,怎样安装，才能使喷水装置最少？再见