浙教版七年级上册 1.3 绝对值 课件(共25张PPT)
文档属性
| 名称 | 浙教版七年级上册 1.3 绝对值 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 735.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-06 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
1.理解绝对值的概念及其几何意义;
2.会求一个数的绝对值,会求绝对值已知的数;
3.理解互为相反数的两个数的绝对值相等.
0
1
2
3
4
-1
-2
-3
大象距原点多远
两只小狗分别距原点多远
(1)甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正。两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作______km,乙车向西行驶10km到达B处,记做_____km。
以O为原点,取适当的单位长度画数轴,并在数轴上标出A、B的位置,则A、B两点与原点距离分别是多少?它们的实际意义是什么?
(2)数轴上表示-4和4的点到原点的距离分别是多少?表示的 和 点呢?
+10
-10
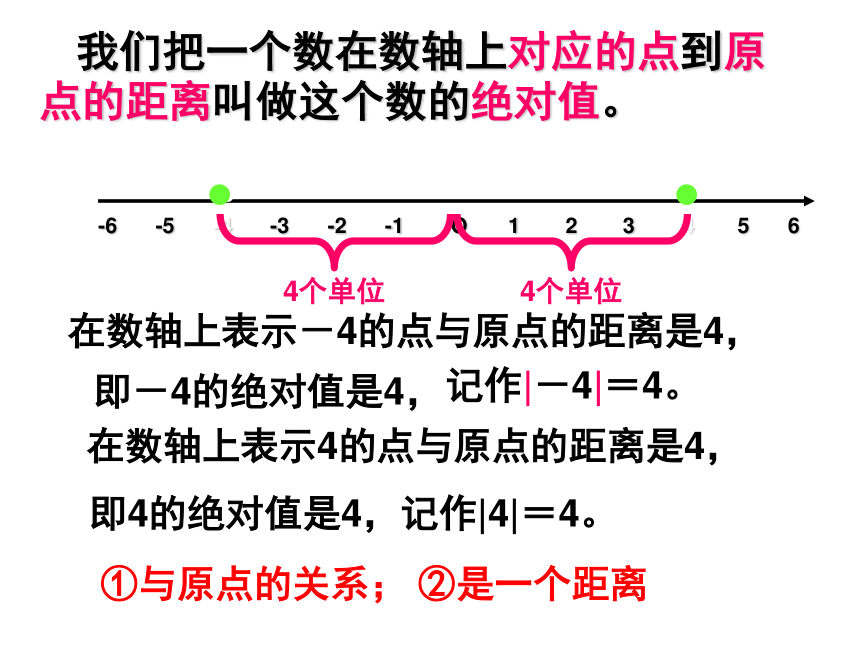
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
O
1
2
3
4
5
6
-1
-2
-4
-3
-5
-6
4
-4
4个单位
4个单位
在数轴上表示-4的点与原点的距离是4,
即-4的绝对值是4,
在数轴上表示4的点与原点的距离是4,
即4的绝对值是4,记作|4|=4。
记作|-4|=4。
①与原点的关系; ②是一个距离
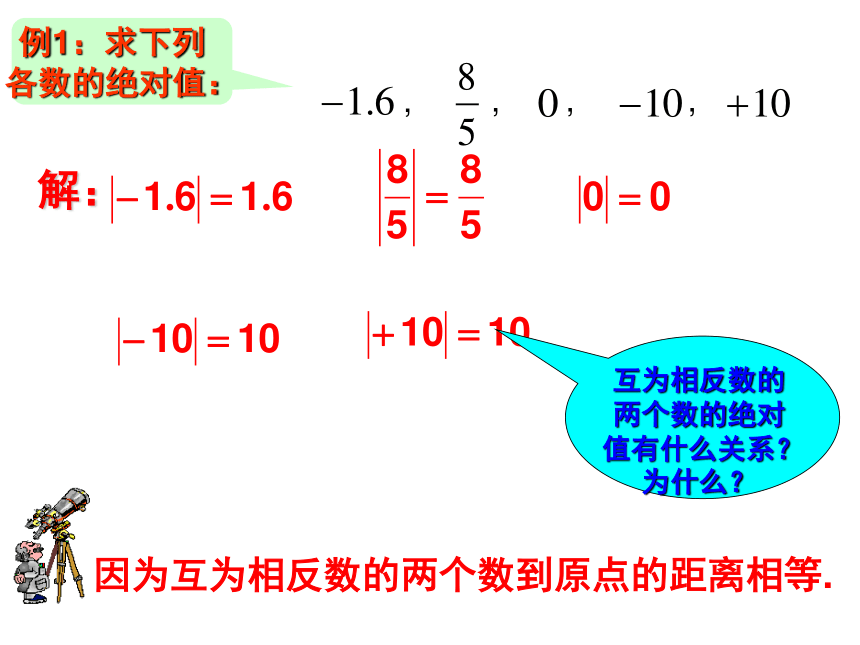
例1:求下列各数的绝对值:
,
,
,
,
解:
互为相反数的两个数的绝对值有什么关系?为什么?
因为互为相反数的两个数到原点的距离相等.
问题1:互为相反数的两个数的绝对值有什么关系?
问题2:一个数的绝对值与这个数有什么关系?
互为相反数的两个数的绝对值相等
正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0
|a|≥0
因为绝对值是距离,所以绝对值不可能是负数
1.绝对值等于0的数是_____;
绝对值等于5.25的正数是______;
绝对值等于5.25的负数是_______;
绝对值等于2的数是________.
0
5.25
-5.25
±2
2.绝对值小于5的整数有 个,分别是 ______________________________.
9
±1,±2,±3,±4,0
3.绝对值不大于5的整数中,最大的数是 ,最小的数是 .
5
-5
4.在数轴上标出各数,并用”<”号将它们连接起来:
|+3|, 4.5, -|-2|, 0, -5.
解:|+3|=3,-|-2|=-2
在数轴上表示为:
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
|+3|
4.5
-|-2|
0
-5
用“<”表示为:
-5<-|-2|<0<|+3|<4.5
1、你能表示下列各数的绝对值吗?并求出他们的绝对值吗? +2,-6,-1.6,10,0
问题:有没有绝对值是自己本身的数 绝对值是自己的相反数的呢
解:|+2|=2,|-6|=6,|-1.6|=1.6,|10|=10,|0|=0
绝对值是本身的数是非负数,即当a≥0时,|a|=a;
绝对值是本身的相反数的数是非正数,即当
a≤0时,|a|=-a;
O
1
2
3
4
5
6
-1
-2
-4
-3
-5
-6
4个单位长度
4个单位长度
M
N
例2、求绝对值等于4的数?
绝对值是同一个正数的数有两个,他们互为相反数.
做一做
1.求绝对值等于0,6.3,-2的数.
解:绝对值为0的数是0,绝对值为6.3的数是±6.3,没有绝对值等于-2的数.
解:两个数的绝对值相等,则这两个数相等或互为相反数.
2.两个数的绝对值相等,则这两个数相等,对吗
(4)绝对值大于 而小于 的整数是______
|5-1| =___
4
1 + |-5| =___
6
| 5 |-|-3 | =___
|-1 | + |-2 | =____
2
3
| +3 |-|-3 | =___
0
(2)绝对值小于 10 的整数有__________个。
(3)绝对值不大于 7 的负整数是_______________
(1)绝对值等于5的数是______________
±5
19
±1, ±2
-1,-2,-3,-4,-5,-6,-7
2、填表:
相反数 绝对值
21
0
-21
21
0
0
3.已知|a-1|+|b+2|=0,则a=_____,b=______
1
-2
4.检查了5个排球的重量(单位:克),其中超过
标准重量的数量记为正数,不足的数量记为负数,
结果如下:
其中哪个球的重量最接近标准?怎样用绝对值
解释排球的重量接近标准重量的程度?
课堂拓展
解:标注为“-0.6”的那个排球质量最接近标准质量,理由如下:
∵|+5|=5,|-3.5|=3.5,|+0.7|=0.7,
|-2.5|=2.5,|-0.6|=0.6
又∵0.6<0.7<2.5<3.5<5
∴标注为“-0.6”的那个排球质量最接近标准
质量.
3.互为相反数的两个数的绝对值相等。
2.一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数,
零的绝对值是零。
1.绝对值的概念:
①与原点的关系 ②是一个距离
1 . 口答
|+5.8|= . |-3.6|= .
|0|= .
|100|= . |-2005|= .
2 .求下列各数的绝对值:
5.8
3.6
0
100
2005
3.计算:
(1) |-2|+3 (2) |-3|×|-5|
(3) |-10.8|-|5.1| (4) |-81|÷|-9|
解:(1)原式=2+3=5
(2)原式=3×5=15
(3)原式=10.8-5.1=5.7
(4)原式=81÷9=9
4、真真假假
(1)一个数的绝对值一定是正数。( )
(2)一个数的相反数一定是负数。( )
(3)互为相反数的两个数的绝对值相等。( )
×
×
√
1、一个数的绝对值是它本身,这个数是______
2、一个数的绝对值是它的相反数,这个数是
_____
3、绝对值不大于3的整数有___个,绝对值小于2.5大于1的整数是________
4、一辆车从A站出发,先向东行驶12km,接着向西行驶8km,然后又向东行驶4km。(1)以原点表示A站,向东为正方向,在数轴上表示出车每次行驶的终点位置。(2)求各次路程的绝对值的和,这个数据有什么实际意义?
5、数轴上到-3距离等于2的数是什么?
0和正数
0和负数
7
±2
-5或-1
1.字母a表示一个数,-a表示什么 -a一定是负数吗 请举个例子说明.
2.如果数a绝对值等于a,那么a可能是正数吗 可能是零吗 可能是负数吗
4.一个数的绝对值可能小于它本身吗
3.如果数a绝对值等于-a,那么a可能是正数吗 可能是零吗 可能是负数吗
1、若︱a︱=3,则a =_____。
2、若︱a-4 ︱+ ︱b︱=0,则a +b = _____。
3、已知数a的绝对值是它本身,数b的绝对值是它的相反数,且 ︱b︱ - a =0,请写出符合条件的a,b两数(至少写3组)。
4、绝对值小于π的整数有_____,它们的和是多少?
1.理解绝对值的概念及其几何意义;
2.会求一个数的绝对值,会求绝对值已知的数;
3.理解互为相反数的两个数的绝对值相等.
0
1
2
3
4
-1
-2
-3
大象距原点多远
两只小狗分别距原点多远
(1)甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正。两辆出租车都从O地出发,甲车向东行驶10km到达A处,记作______km,乙车向西行驶10km到达B处,记做_____km。
以O为原点,取适当的单位长度画数轴,并在数轴上标出A、B的位置,则A、B两点与原点距离分别是多少?它们的实际意义是什么?
(2)数轴上表示-4和4的点到原点的距离分别是多少?表示的 和 点呢?
+10
-10
我们把一个数在数轴上对应的点到原点的距离叫做这个数的绝对值。
O
1
2
3
4
5
6
-1
-2
-4
-3
-5
-6
4
-4
4个单位
4个单位
在数轴上表示-4的点与原点的距离是4,
即-4的绝对值是4,
在数轴上表示4的点与原点的距离是4,
即4的绝对值是4,记作|4|=4。
记作|-4|=4。
①与原点的关系; ②是一个距离
例1:求下列各数的绝对值:
,
,
,
,
解:
互为相反数的两个数的绝对值有什么关系?为什么?
因为互为相反数的两个数到原点的距离相等.
问题1:互为相反数的两个数的绝对值有什么关系?
问题2:一个数的绝对值与这个数有什么关系?
互为相反数的两个数的绝对值相等
正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0
|a|≥0
因为绝对值是距离,所以绝对值不可能是负数
1.绝对值等于0的数是_____;
绝对值等于5.25的正数是______;
绝对值等于5.25的负数是_______;
绝对值等于2的数是________.
0
5.25
-5.25
±2
2.绝对值小于5的整数有 个,分别是 ______________________________.
9
±1,±2,±3,±4,0
3.绝对值不大于5的整数中,最大的数是 ,最小的数是 .
5
-5
4.在数轴上标出各数,并用”<”号将它们连接起来:
|+3|, 4.5, -|-2|, 0, -5.
解:|+3|=3,-|-2|=-2
在数轴上表示为:
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
|+3|
4.5
-|-2|
0
-5
用“<”表示为:
-5<-|-2|<0<|+3|<4.5
1、你能表示下列各数的绝对值吗?并求出他们的绝对值吗? +2,-6,-1.6,10,0
问题:有没有绝对值是自己本身的数 绝对值是自己的相反数的呢
解:|+2|=2,|-6|=6,|-1.6|=1.6,|10|=10,|0|=0
绝对值是本身的数是非负数,即当a≥0时,|a|=a;
绝对值是本身的相反数的数是非正数,即当
a≤0时,|a|=-a;
O
1
2
3
4
5
6
-1
-2
-4
-3
-5
-6
4个单位长度
4个单位长度
M
N
例2、求绝对值等于4的数?
绝对值是同一个正数的数有两个,他们互为相反数.
做一做
1.求绝对值等于0,6.3,-2的数.
解:绝对值为0的数是0,绝对值为6.3的数是±6.3,没有绝对值等于-2的数.
解:两个数的绝对值相等,则这两个数相等或互为相反数.
2.两个数的绝对值相等,则这两个数相等,对吗
(4)绝对值大于 而小于 的整数是______
|5-1| =___
4
1 + |-5| =___
6
| 5 |-|-3 | =___
|-1 | + |-2 | =____
2
3
| +3 |-|-3 | =___
0
(2)绝对值小于 10 的整数有__________个。
(3)绝对值不大于 7 的负整数是_______________
(1)绝对值等于5的数是______________
±5
19
±1, ±2
-1,-2,-3,-4,-5,-6,-7
2、填表:
相反数 绝对值
21
0
-21
21
0
0
3.已知|a-1|+|b+2|=0,则a=_____,b=______
1
-2
4.检查了5个排球的重量(单位:克),其中超过
标准重量的数量记为正数,不足的数量记为负数,
结果如下:
其中哪个球的重量最接近标准?怎样用绝对值
解释排球的重量接近标准重量的程度?
课堂拓展
解:标注为“-0.6”的那个排球质量最接近标准质量,理由如下:
∵|+5|=5,|-3.5|=3.5,|+0.7|=0.7,
|-2.5|=2.5,|-0.6|=0.6
又∵0.6<0.7<2.5<3.5<5
∴标注为“-0.6”的那个排球质量最接近标准
质量.
3.互为相反数的两个数的绝对值相等。
2.一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数,
零的绝对值是零。
1.绝对值的概念:
①与原点的关系 ②是一个距离
1 . 口答
|+5.8|= . |-3.6|= .
|0|= .
|100|= . |-2005|= .
2 .求下列各数的绝对值:
5.8
3.6
0
100
2005
3.计算:
(1) |-2|+3 (2) |-3|×|-5|
(3) |-10.8|-|5.1| (4) |-81|÷|-9|
解:(1)原式=2+3=5
(2)原式=3×5=15
(3)原式=10.8-5.1=5.7
(4)原式=81÷9=9
4、真真假假
(1)一个数的绝对值一定是正数。( )
(2)一个数的相反数一定是负数。( )
(3)互为相反数的两个数的绝对值相等。( )
×
×
√
1、一个数的绝对值是它本身,这个数是______
2、一个数的绝对值是它的相反数,这个数是
_____
3、绝对值不大于3的整数有___个,绝对值小于2.5大于1的整数是________
4、一辆车从A站出发,先向东行驶12km,接着向西行驶8km,然后又向东行驶4km。(1)以原点表示A站,向东为正方向,在数轴上表示出车每次行驶的终点位置。(2)求各次路程的绝对值的和,这个数据有什么实际意义?
5、数轴上到-3距离等于2的数是什么?
0和正数
0和负数
7
±2
-5或-1
1.字母a表示一个数,-a表示什么 -a一定是负数吗 请举个例子说明.
2.如果数a绝对值等于a,那么a可能是正数吗 可能是零吗 可能是负数吗
4.一个数的绝对值可能小于它本身吗
3.如果数a绝对值等于-a,那么a可能是正数吗 可能是零吗 可能是负数吗
1、若︱a︱=3,则a =_____。
2、若︱a-4 ︱+ ︱b︱=0,则a +b = _____。
3、已知数a的绝对值是它本身,数b的绝对值是它的相反数,且 ︱b︱ - a =0,请写出符合条件的a,b两数(至少写3组)。
4、绝对值小于π的整数有_____,它们的和是多少?
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
